基于改进FI-NN 算法的时域超前变桨控制

2021-05-08秦佳晖曾宪文高桂革

上海电机学院学报 2021年2期

秦佳晖, 曾宪文, 高桂革

(上海电机学院a.电子信息学院;b.电气学院, 上海201306)

随着我国风电技术的发展,风电的单机容量越来越大,更大的转动惯性和迟滞的系统响应为传统的变桨控制方式带来了挑战。对此,国内外学者对风速模型和变桨控制系统进行了广泛的研究。文献[1-2]分别使用了神经网络和模糊控制作为变桨前馈控制部分,改善了机组系统滞后。文献[3]利用卡尔曼滤波器设计了一种前馈变桨控制方法,改善了机组系统时滞。文献[4]结合差分算法和粒子群优化算法,减少了变桨进入稳定状态的时间。文献[5]结合多种不同的模糊结构和滑模控制,使变桨模型适用于不同工况。文献[6]设计了一种部分离线型的模糊PI前馈变桨控制器,减轻了在线模糊PI前馈变桨控制的计算负担。文献[7]在BP神经网络预测变桨的基础上加入了参数预处理。文献[8-10]以粒子群优化算法为主,混合了多种不同算法,取得了良好的改进效果。

虽然不同机器学习算法的组合可以改进变桨控制系统的性能,但是组合算法必须在更好的控制性能与引入更多的机器学习类算法固有缺点之间进行取舍[11]。分形插值是一种针对非线性对象的计算方法,其常被用于股市曲线预测,非常符合风速的变化特征[12-14]。本文改进了经典分形插值—神经网络预测(Fractal Interpolation-Neural Network,FI-NN),并基于改进FI-NN提出了一种时域超前变桨控制方法。仿真验证了FI-NN预测对变桨控制性能的提高,同时分形插值是一种非机器学习算法,不会引入更多机器学习算法的固有缺点,如易陷入局部最优和需要大量训练样本。

1 分形插值函数与风电变桨原理

1.1 分形插值函数

分形是一门研究几何图形自相似性的学科,分形插值使用了迭代函数系统(Iteration Function System,IFS)进行插值,所以分形插值是一种非线性图形的插值方法。IFS通过构建迭代方程得到插值点:

式中:ωi(x j)和ωi(y j)分别为第i个IFS系统中第j个分形插值点的横坐标和纵坐标;X j和Y j分别为待插值曲线中第j个离散数据点的横坐标和纵坐标;d i为自由变量,决定IFS在映射过程中的垂直比例缩放,又称为垂直比例因子;a i、e i、c i、f i均为IFS中的中间参数,其值为

式中:X i、Y i、X i+1、Y i+1分别为待插值曲线第i和i+1组离散数据的横坐标和纵坐标;X0、Y0分别为待插值曲线起始离散数据的横坐标和纵坐标;X N、Y N分别为待插值曲线末尾离散数据的横坐标和纵坐标。

1.2 变桨控制原理

当双馈异步风力发电机(Doubly Fed Induction Generator,DFIG)功率输出超过额定功率时,需要通过增大桨距角从而降低风轮吸收的功率。风轮吸收功率为

式中:ρ为空气密度;R为叶片半径;v为风速;Cp为风能利用系数;λ为叶尖速比;β为桨距角(增大桨距角可使Cp变小,从而降低叶轮吸收的功率[15])。

图1 风速数据的EMD分解结果

2 基于改进FI-NN的风速预测

2.1 风速分形插值理论依据

通过对某实验室的风速数据进行经验模态分解(Empirical Mode Decomposition,EMD)和希尔伯特变换(Hilbert Transform,HT),发现不同采样频率风速数据分频分量之间存在着比例关系,如图1所示。图1中横坐标是以小时为采样周期的风速数据中的频率分量,纵坐标是以分钟为采样周期的风速数据中的频率分量。两者组成的坐标可以近似地拟合成一条直线,说明不同采样频率风速在频率上具有分形的特点,而分形插值则可以通过低采样频率数据预测出高采样频率数据。

2.2 改进的FI-NN风速预测算法

改进的FI-NN 风速预测算法流程如图2所示。图2中虚线框部分为改进部分。经典FI-NN中的d i采用随机变量,使分形得到的曲线垂直尺度缩放存在误差。本文通过分析得到历史d i变化曲线,然后利用神经网络对d i进行预测,从而提高FI-NN的预测精度。

预测算法的总体步骤可以分为以下3 步:①利用梯度下降法得到历史d i曲线;②通过神__经网络对未来d i与大致风速走向进行预测;③利用分形插值得到风速预测数据。

图2 风速预测流程

为了确定d i的历史变化曲线,本文利用梯度向量法分析历史d i变化过程,以线性相关系数作为梯度下降法中的损失函数,有________________

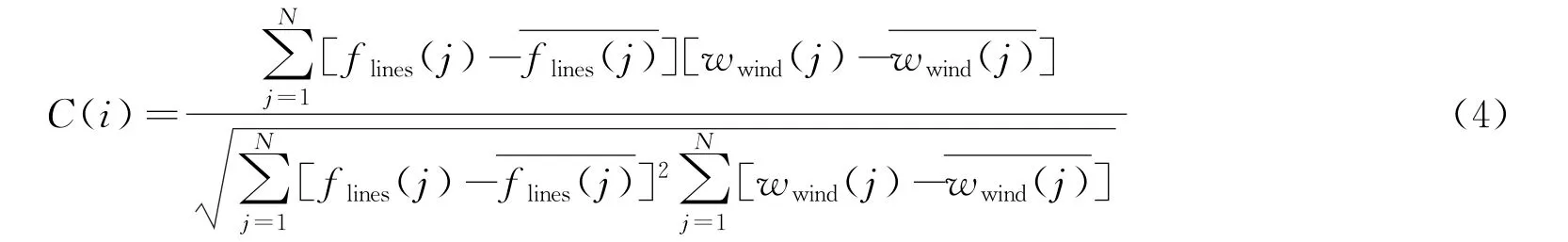
式中:i为分形区间段序号;C(i)为线性相关系数;flines(j)为分形插值得到的拟合曲线;wwind(j)为实际历史风速曲线;j为一个分形区间段内的离散数据序号;N为总的离散数据个数。

根据下式更新得到历史d i变化数据为(式中d i表达为d(i))

式中:Lr为梯度速率。

2.3 改进FI-NN的风速预测仿真

利用历史风速数据和d i数据训练BP神经网络并预测,得到大范围内的低频风速与d i的未来趋向;再将BP神经网络预测数据重新分形插值,得到高精度风速预测数据。仿真得到的4月11日前140 min,以1 min为离散间隔的风速预测结果对比,如图3所示。图3中,实线为本文经过d i分析改良的FI-NN 分形插值预测曲线,虚线为实际风速曲线,带点虚线为传统随机d i的FI-NN 预测曲线。可以看到,本文的方法有效减少了预测误差。神经网络训练数据均来自于某实验室4月4日～10日的风速离散数据。

图3 风速预测图

3 基于改进FI-NN的变桨控制

3.1 风速前馈控制

前馈控制可以消除系统响应迟滞,快速变桨。对DFIG的前馈功率控制有

式中:Pwaste为从叶轮吸收功率到风力发电机输出功率之间的功率耗损,其值一般在2%到5%之间,本文为2.5%;Pgen为DFIG稳态输出功率。

求解式(6)即可得到Pgen和v下的前馈β值。

3.2 基于改进FI-NN的时域超前变桨控制

式(6)中v为实时风速,本文将v改为预测风速,实现了时域超前变桨控制。时域超前变桨控制的流程如图4所示。

图4中,v、Pgen、DFIG 转速、ρ和R为输入参数,预测β值为输出参数。DFIG功率控制方程模块利用式(6)和输入参数求解,在预测风速条件下,能够将DFIG的Pgen稳定在额定功率的β值。求解得到的β值与前馈控制下的β值相比,在时域上呈现超前特性,故称为时域超前变桨控制。在时域超前变桨控制中,通过计算v得到的β值将被直接发送给变桨执行机构,从而在风速变化到来前提前变桨。

图4 时域超前变桨控制流程

经典变速变桨可以做到在协同控制区内对Pgen曲线削峰填谷。但当DFIG转子轴转速ωgen达到最大值时,转子会因为无法吸收更多的动能而无法削去Pgen曲线多余的峰值,这时对Pgen曲线的控制就需要尽量避免出现波峰。这种情况下时域超前变桨的特性便优于经典变速变桨。虽然转子无法通过吸收更多的动能削去Pgen曲线多余的峰值,但是仍可以提取储存于转子中的动能补充Pgen曲线的低谷。时域超前变桨可以做到在ωgen超速前主动降速,避免因前馈控制而产生的ωgen和Pgen双超调情况。

具体的Pgen控制改进过程如图5所示。图5中,标注序号为①、②、③的曲线分别为改进前的Pgen曲线、时域超前变桨后的Pgen曲线和最终经过转子动能补偿的Pgen曲线。DFIG 首先通过时域超前变桨消除变桨机构在时滞上的影响和Pgen上的超调波峰,并提前使β达到预测风速工作点。此时曲线①被调整为曲线②,然后通过提取转子中的动能弥补时域超前变桨带来的波谷,有效避免了ωgen陷入因控制不及时而产生的超速,此时曲线②被调整为曲线③。

图5 预测控制下的功率超调改善

3.3 双模控制切换判据

经典变速变桨控制可以储存转子动能,稳定Pgen曲线,时域超前变桨控制可以避免ωgen超速和Pgen超调。两种控制方法之间切换的判据,一是预测风速高于实时风速,该情况下未来风轮功率会猛增,从而导致ωgen可能产生超调;二是判断预测风速增长带来的Pgen增长是否会引起ωgen超速。如果风轮吸收的Pgen增长会使得ωgen超速,那么预测周期内的齿轮箱增速量一定大于前一时刻转速与额定转速的转速差,即齿轮箱增速率在风速预测时间周期内的积分存在不等式关系,即

式中:ΔPwind为实时前馈控制下的功率偏差;Prate为DFIG额定功率;k为齿轮箱传动比;ΔTpre为预测点离散间隔;ωrate为额定转速;ωt为风轮转速;Jg为DFIG转动惯量;Jwind为风轮转动惯量。

当两个条件都满足时,说明风速所引起的转速增量大于转速裕度,经典变速变桨控制切换为时域超前变桨控制,避免转速超速。

4 基于改进FI-NN的时域超前变桨控制仿真

仿真对象为建立在Simulink平台上的额定功率2 MW 的DFIG。变桨采用了一阶惯性环节模拟变桨产生的迟滞,控制模型输入为2.3节得到的预测风速,DFIG 的初始状态为:ωgen=250 rad/s,ωrate=250 rad/s,Prate=2 MW,变桨指令由3.2节中时域超前变桨控制系统给出。经典变速变桨控制和时域超前变桨控制在ωgen临界点附近运行时的各项输出对比如图6所示。

图6中,虚线为前馈控制下的变速变桨阶段DFIG各项输出曲线,实线为加入了时域超前变桨预测控制的DFIG各项输出参数曲线。从图6(a)和图6(d)可以看到,当预测到风速猛增可能导致ωgen和Pgen超调时,预测控制进行了时域超前变桨。从图6(b)中可以看到,预测控制在时域超前变桨时使得ωgen得到了下降,有效限制了ωgen超速。图6(c)显示出预测控制消除了前馈控制因变桨跟踪误差所产生的Pgen误差。仿真显示,即便预测风速具有一定的偏差,预测控制仍然在消除ωgen和Pgen的超调上表现良好。