Magnus减摇装置及其升/阻力特性分析
2021-05-08梁利华姜寅令亢武臣赵朋
梁利华,姜寅令,2,亢武臣,赵朋
(1.哈尔滨工程大学 自动化学院,黑龙江 哈尔滨 150001;2.东北石油大学 电气信息工程学院,黑龙江 大庆 163318;3.中国石化石油工程技术研究院,北京 100101;4.唐山学院 交通与车辆工程系,河北 唐山 063000)
Magnus效应原理的圆柱形旋转式减摇装置是一种新型的低航速减摇装置[1-3]。与传统减摇鳍不同,Magnus减摇装置使用的是快速旋转的圆柱,根据转速大小和方向的不同,产生向上或向下的升力,进而产生抵抗横摇的稳定力矩,从而达到减摇的效果。基于Magnus效应的船用减摇装置的设计思想出现在Pangalila[4]、Kollenberger[5]的专利中。Koop[6]研发出马格纳斯效应减摇装置并完成实船试验。2012年Magnus减摇装置产品面向市场,目前能够成功生产Magnus减摇装置的厂商仅限于RotorSwing和Quantum公司,中国市场的Magnus减摇装置仍处空白,哈尔滨工程大学正致力于Magnus减摇装置的研发。目前,圆柱绕流问题的研究大多集中在低雷诺数,非旋转或二维仿真研究[7-9]。高雷诺数下旋转圆柱绕流的三维仿真研究较少,且人们更多关注的是雷诺数、斯特劳哈尔数、转速比对升/阻力以及圆柱后方尾迹变化的影响[10-12],较详细的关于升/阻力特性与来流速度、转速关系的研究很少,且目前已知的相关实验研究仅有风洞试验和低转速的水池实验。Lafay[13]通过大量的实验研究了Magnus效应产生的升力,指出投影面积相同的情况下,旋转圆柱产生的Magnus力的大小约是翼面的2倍。Prandtl[14]进行了圆柱绕流的可视化研究,指出其升力系数最大为4π,该升力系数大约是飞机机翼通常得到的数值的10倍。Reid[5]认为单位投影面积上,转子翼的升力相当于传统减摇鳍的7倍,但没有给出具体的转速和航速等约束条件。早期的一些实验研究发现,长径比以及转速比对升/阻力的影响较大,但各变量之间的联系规律尚不明确,其应用范围也不清楚[14-15]。Karabelas[16]采用大涡模拟的方法在小转速比(α<2)情况下对旋转圆柱绕流问题进行了二维仿真研究,认为阻力随着转速的增加而减小,由于其采用的转速比比较低,范围较窄,其结果没有能够呈现出1个较完整的发展态势。Chen等[17]在较大的转速比范围内采用水池实验测量了长度0.59 m,半径分别为0.319、0.267、0.216和0.102 m带同轴旋转端板的旋转翼水动力特性,认为升力系数和阻力系数取决于转速比。其实验由于受马达限制,转速较低(小于600 r/min),且来流速度也较小,导致其升/阻力系数较高,测量结果表明升力系数可以超过4π。虽然文献[17]的研究结果表明Prandtl极限可以被超越,但是符合Prandtl极限的研究也依然存在。Reid[15]采用风洞试验对旋转圆柱绕流问题进行了研究,转速高达1 800~3 600,但是测得的升力系数没有超过4π。Chew等[18]研究了雷诺数100,转速比6时的升力系数,其值也没有超过Prandtl极限。
由于高雷诺数下旋转圆柱绕流问题的复杂性,Magnus减摇装置的水动力特性与各量之间的关系尚不明确,相关的产品宣传资料只是对升/阻特性做了粗略的概括。为了研究不同航速和转速条件下,转子翼的升/阻特性,本文结合Quantum公司推出的Maglift型减摇装置的设计尺寸,对长度2.5 m,直径350 mm的转子翼,在航速4~12 kn,转速500~1 800 r/min范围内开展了三维仿真研究。
1 几何模型与网格划分
根据Magnus减摇装置的工作场合,建立流场的三维几何模型(如图1所示),流场尺寸为(5 000+H)×(5 000+D)×(5 000+D)mm,其中H为转子翼长度,D为直径。转子翼并未放置到流场的几何中心,而是紧贴一侧壁面安装(相当于船壁),另一端为自由端,自由端的中心为坐标原点。由于本次仿真对尾迹的关注程度不高,所以并没有采用通常圆柱绕流问题的下游加长处理。采用ANSYS经典界面构建仿真模型及网格划分,图1和图2是转子绕流的流场区域的三维网格,采用以圆柱的中心为圆心的直线网格划分方式,由于圆柱周围近壁面和分离点附近尾流区的流动较为复杂,在圆柱近壁区对网格进行了加密处理,且生成的网格都是正交度很高的六面体网格。圆柱展向每隔100 mm等分一层,圆柱周向等分100份,圆柱展向外水域等分了20层。
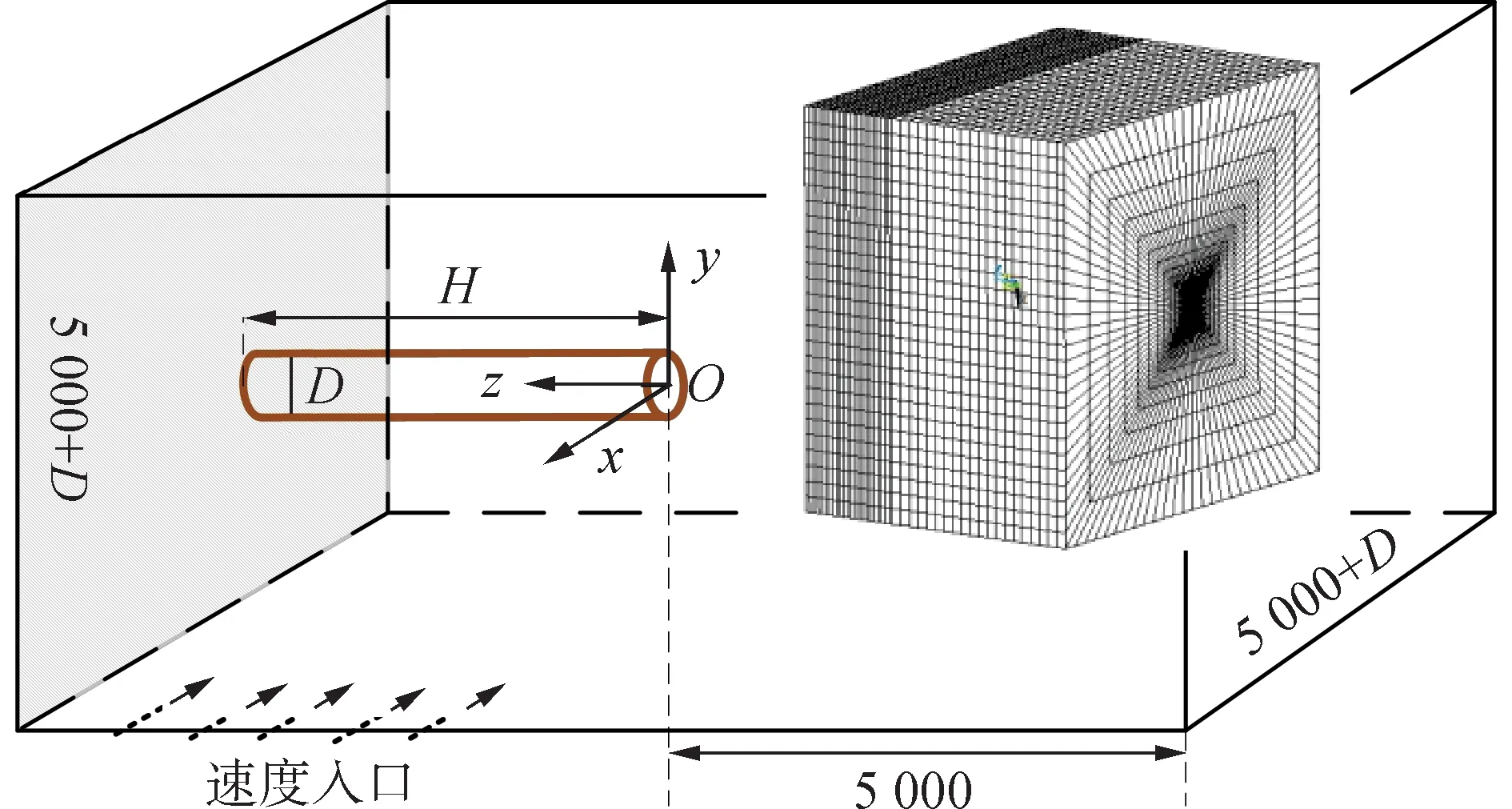
图1 旋转翼绕流流动计算域与三维网格Fig.1 Computational model and 3-D mesh of flow around a rotating wing
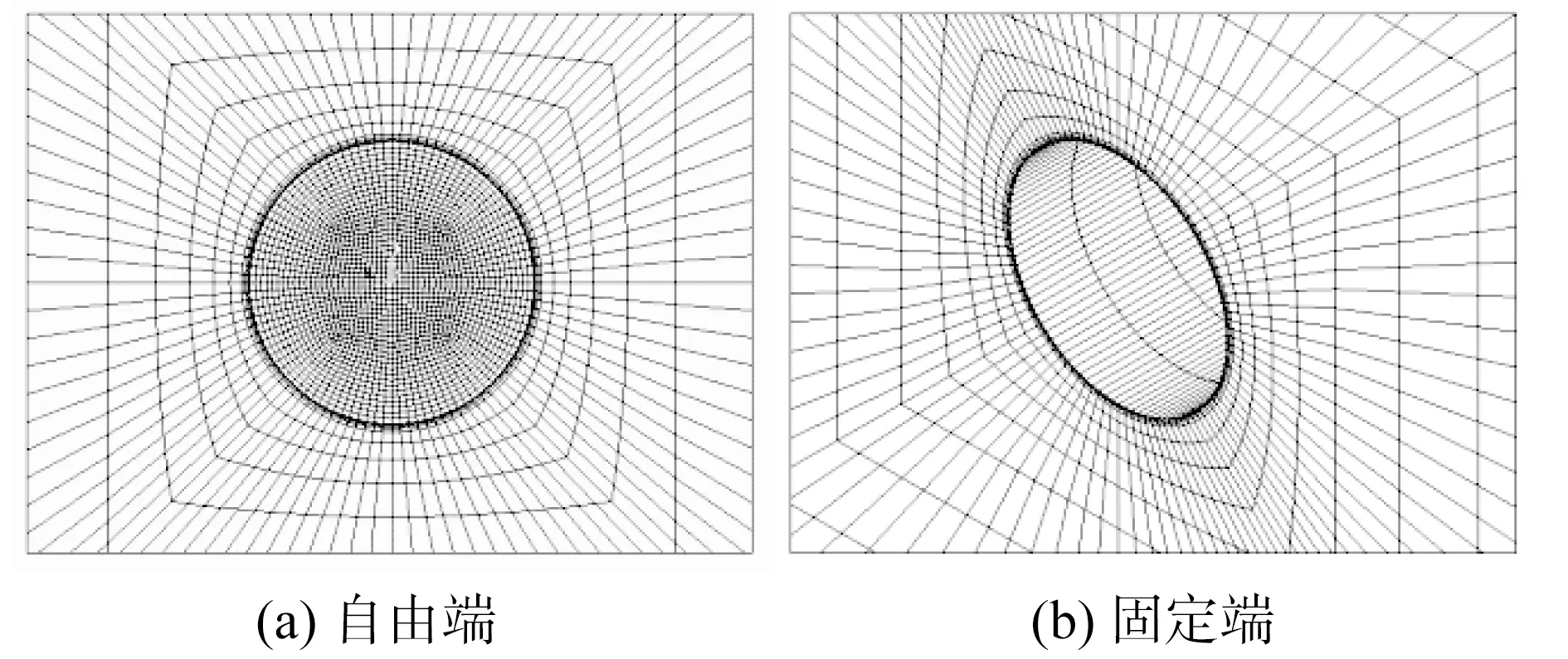
图2 近壁面网格Fig.2 Near-wall grids
为了验证网格划分的有效性并对仿真结果的合理性进行验证。图3所示为将本文所采用模型的计算结果与前人结果进行比对。图3(a)为文献[17,19-20]转子翼的升力系数结果与本文仿真结果的对比。本文的仿真结果与文献[17,19-20]的实验结果吻合较好,升力系数随着转速比的提高而提高,变化趋势一致,但与Karabelas[16]的大涡二维仿真结果偏差较大,分析主要是二维模拟忽略了旋转圆柱绕流的三维效应导致的。图3(b)为转子翼的阻力系数与Chen等[17]的实验结果对比。二者变化趋势基本一致,都在初始区阻力系数降低,进入增加区快速升高。但二者也存在差异,Chen等[17]水池实验阻力系数略高于本文得到的结果,分析原因前者实验的转子采用了端部突出挡板增加了阻力,并且二者的转子尺寸、转速等实验条件也不相同。因此,认为本次仿真的数据基本合理。

图3 升/阻力系数与转速比的关系Fig.3 Lift and drag coefficients versus spin ratio speeds
2 数值结果及分析
将研究的三维旋转圆柱绕流流动区域的速度分别设定为U(x),V(y)和W(z) 3个方向。圆柱上游为速度入口,均匀来流,入口边界条件为,速度u=V,v=0,w=0;圆柱下游为计算域的出口,出口边界条件为:
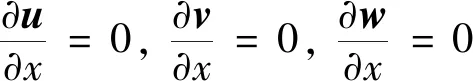
(1)
转子翼固定端一侧壁面和旋转翼表面以及自由端圆形盖板表面均设定为无滑移壁面,即流体在固体表面的流动速度等于固体表面的运动速度,流域的其他3个壁面边界条件都为Opening。在ANSYS-CFX中通过参考坐标系的方法,给转子设置旋转速度。建立图1所示以圆柱自由端为原点的直角坐标系,再建立变量表达式。圆柱表面线速度为:

(2)
式中:n为转速;R为圆柱半径。
则将线速度进行分解,则圆柱表面某点(x,y,z)的速度为:
(3)
本次仿真采用模拟计算中使用频率最高的k-ε湍流模型,k-ε模型适合绝大多数的工程湍流模型。
2.1 升力分析
在一定来流下,旋转圆柱体上产生的Magnus力的理论计算可基于库塔茹可夫斯基原理[21],转子翼上产生的升力Fl及旋涡强度Γ为:
Fl=ρVHΓ
(4)
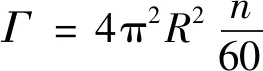
(5)
式中:ρ为液体密度;V为来流速度;n为转子角速度。转子升力与航速、转速的一次方成正比(传统翅片型减摇鳍产生的升力与航速平方成正比),航速的降低对转子翼升力影响相对较小,可通过提高转子转速来提高转子翼升力。图4为转子翼升力与航速、转速的关系。仿真结果表明,航速或转速的提高能够明显增加转子翼升力。航速较低时,转子翼升力几乎随着转速线性增加,增速缓慢,随着航速的增大,升力随着转速增加迅速。转子翼升力Fl及升力系数Cl为:
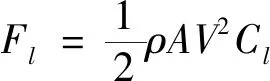
(6)

(7)
式中:A为转子的投影面积;α为转速比,是圆柱表面速度与自由来流速度的比值。升力系数与α成正比,但这是在理想假设前提下得出的结论,实际上由于边界层条件不能始终满足以及船舶自身运动等的影响,升力系数要比理论值小很多。从图4(c)、(d)可以看出,在仿真范围内,转子翼的升力系数没有超过4π。但即便如此,转子翼最小的升力系数(约为4.75)也是传统减摇鳍(约为1)的4倍以上,尤其在低航速时(航速8 kn以下)优势更为明显。
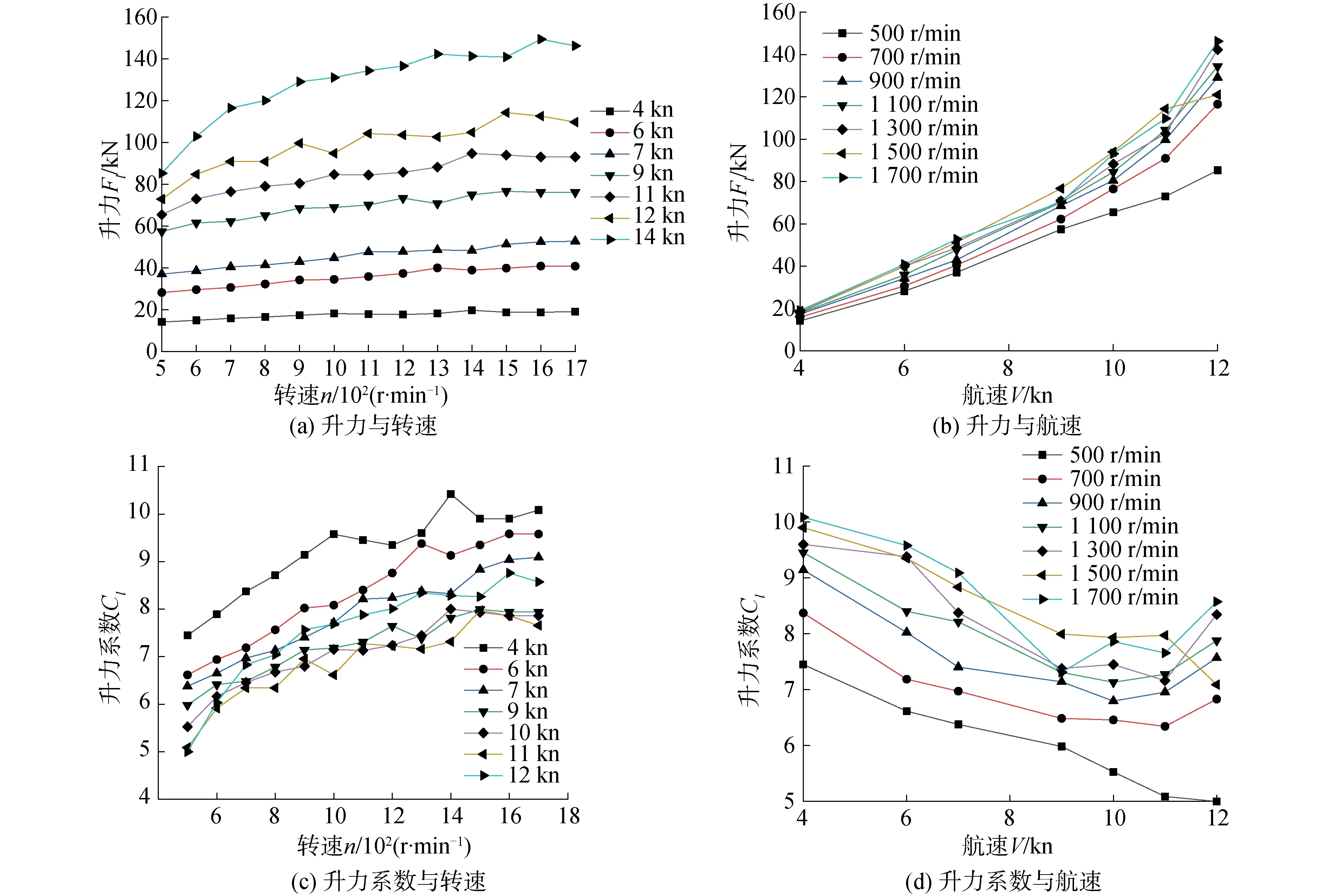
图4 转子翼升力、升力系数与转速和航速的关系Fig.4 The lift and lift coefficients versus ship speed and rotary speeds and ship
图6、7为航速7 kn且转速变化时,转子翼的压力云图和流线图。图6(a),高压区在转子翼上表面分布并不均匀,随着转速的提高,高压区向转子翼两端移动,且压力分布并不对称,压力中心更靠近自由端一侧,这在支撑轴承的安装取位上是一个不容忽视的问题,同时也证明了二维仿真结果会导致很大的偏差。由于转速较高,转子翼后方尾迹没有明显的旋涡脱落产生,见图6(b)。

图6 转子翼的压力云图Fig.6 Clouds maps for the rotor wing

图7 转子翼的流线图Fig.7 Streamlines maps for the rotor wing
为了得到升力与航速、转速的关系,采用图8所示非线性曲面拟合,得到关系式为:
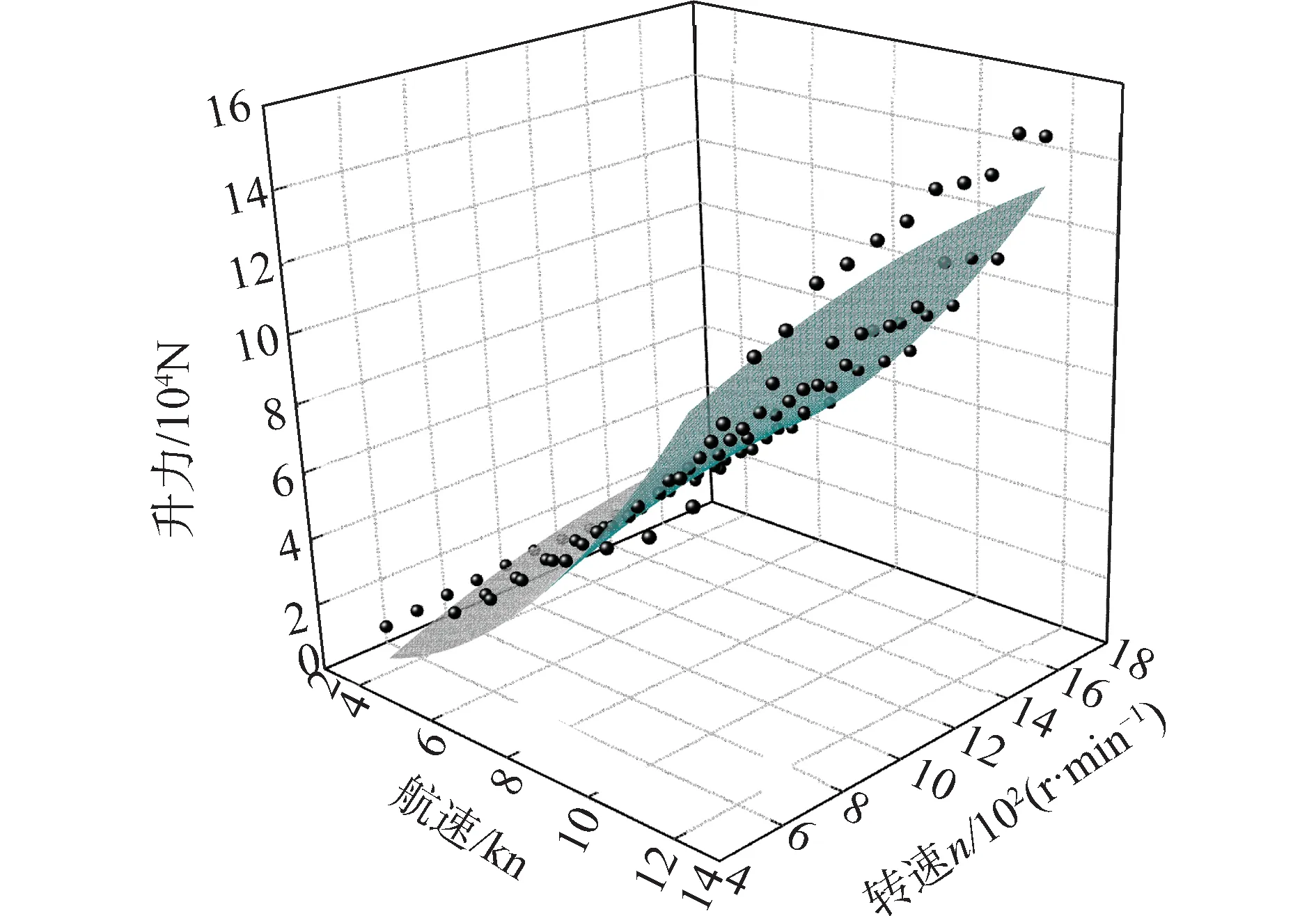
图8 升力与转速和航速的关系及拟合曲面Fig.8 The lift versus ship speeds and rotary speeds and its fitting surfaces
Fl=-22 254.24-3 250.56V+53.95n+
1 023.26V2-0.015n2
(8)
2.2 阻力与阻力系数
目前关于旋转圆柱绕流的阻力与转速之间的关系尚没有清晰的表达式存在。从本文仿真结果来看,阻力随着转速或航速的增加而增加,在低航速时,阻力呈现出与转速成正比的关系,图5(a)、(b)。在较低转速比的情况下升阻力系数的变化趋势和文献[22]的结果部分相符合,阻力系数随着转速比快速增加。NACA翼型的减摇鳍阻力系数小于0.6,结合图5(c)、(d),可以看出这种转子翼比鳍片鳍有更大的流动阻力。因此寻求减小阻力的方法与技术是Magnus减摇装置生产厂商的一个关注重点。通常在航速较低时(一般指8 kn以下),转子上产生的航行阻力虽然比传统减摇鳍大,但是由于航速较低,整个量值较小,一般不采取减阻措施。但是在较高航速时,Magnus旋转翼上压力阻力迅速增加,能耗明显。目前,RotorSwing和Quantum公司Magnus减摇装置的RAKE功能可在一定程度上减小航行阻力。当航速增加时,通过像飞机上的机翼那样向后折叠旋翼,阻力大大减小,但不会对升力造成太大影响。
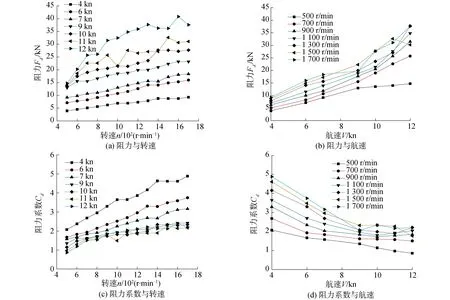
图5 转子翼阻力、阻力系数与转速、航速的关系Fig.5 The drag and drag coefficients versus rotary speeds and ship speeds
3 结论
1)旋转翼上的升力、阻力均随着转速或航速的增加而增加,在低航速条件下(约小于9 kn),旋转翼上的升力、阻力几乎与航速和转速成正比关系,随着航速的增加呈现出非线性关系;
2)旋转翼的升力系数与阻力系数随着转速的增加而增加,随着航速的增加而减小。随着航速继续提高,升力系数又呈现出回升的态势;
3)与传统翅片型减摇鳍相比,Magnus减摇装置拥有更大的升力系数。
与传统翅片型减摇鳍相比,Magnus减摇装置的流动阻力也相当大,寻求更好的减阻措施是今后的一个关注重点。
