一种端到端的织物颜色自动预测框架

周奕军，陈 昭，李 悦，纪柏林，王国栋，刘国华

(东华大学 a.计算机科学与技术学院；b.化学化工与生物工程学院，上海 201620)

传统的织物染色工艺中，染料配方设计具有人工经验依赖性强、耗时费力等特点，并且由于生产线环境与配色实验室环境存在较大差异，染色产品的颜色可能偏离预期，需凭借人工经验修改染料配方。为减少调节染色处方的工作量、节省染料成本、降低污染，有必要寻找提高织物染色准确率和生产效率的方法。除可以从化工方面改进织物染色外，还可应用计算机技术，特别是近年来兴起的人工智能技术。通过应用计算机技术分析历史工艺参数来预测织物颜色，可有效降低染色误差。Senthilkumar等[1-2]使用人工神经网络(artificial neural network, ANN)预测染色的上色时间和固色时间，以及织物的颜色(CIELAB值)；Kandi等[3]使用遗传算法(genetic algorithm，GA)预测织物的染色配方。然而，文献[1-3]只考虑了染料配方对织物最终颜色的影响，忽略了染色过程中众多关键生产参数如织物白度、染料浓度等的影响。Balci等[4]考虑到了染色过程中若干个对颜色有影响的关键生产参数，但只应用了现有的机器学习模型，而未深层次研究模型内部结构，也未提出针对染料配方数据集特征的模型优化方法。诸如此类的研究虽然在特定应用上取得了一定成效，但缺乏系统的理论框架，难以适应不同的配方设计需求。

基于对山东省华纺股份有限公司(简称“华纺”)生产记录的分析，提出一种端到端的织物颜色自动预测框架，期望对织物染色给予精准的理论指导和有力的辅助作用。出于效果和效率的综合考虑，采用多维支持向量回归机(multi-dimensional support vector regressor，M-SVR)、反向传播神经网络(back propagation neural network，BPNN)和遗传算法初始化的BPNN(GA-BPNN)等3种具体模型来实现织物颜色的端到端预测。选择BPNN和M-SVR模型的主要原因是：这两个模型都可以直接处理多维向量样本，并且可以通过描述数据内在的非线性结构，实现非线性拟合；M-SVR在处理少量样本数据时效果较好，而BPNN能够有效处理大容量样本数据。鉴于人工神经网络作为一种较为先进的配色预测方法，已被用于色纺纱[5]和织物染色[6]的计算机配色，将BPNN作为一种备选模型。选用GA初始化BPNN的原因是，GA在搜寻最优解问题方面具有良好的性能，可以用来搜寻BPNN参数的最优初始值，降低参数随机初始化给模型性能带来的不稳定性和不确定性，从而加快BPNN的收敛，提升织物颜色的预测效率。还使用径向基函数(radial basis function, RBF)网络做对比算法，RBF网络属于机器学习的一种基础网络，通过和RBF网络进行对比以检验提出的模型。

1 方 法

1.1 数据建模

设数据样本为x∈Rn，先验标记信息为y∈Rm，一般地，有监督机器学习框架下的多维回归问题描述如下：

(1)

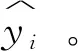
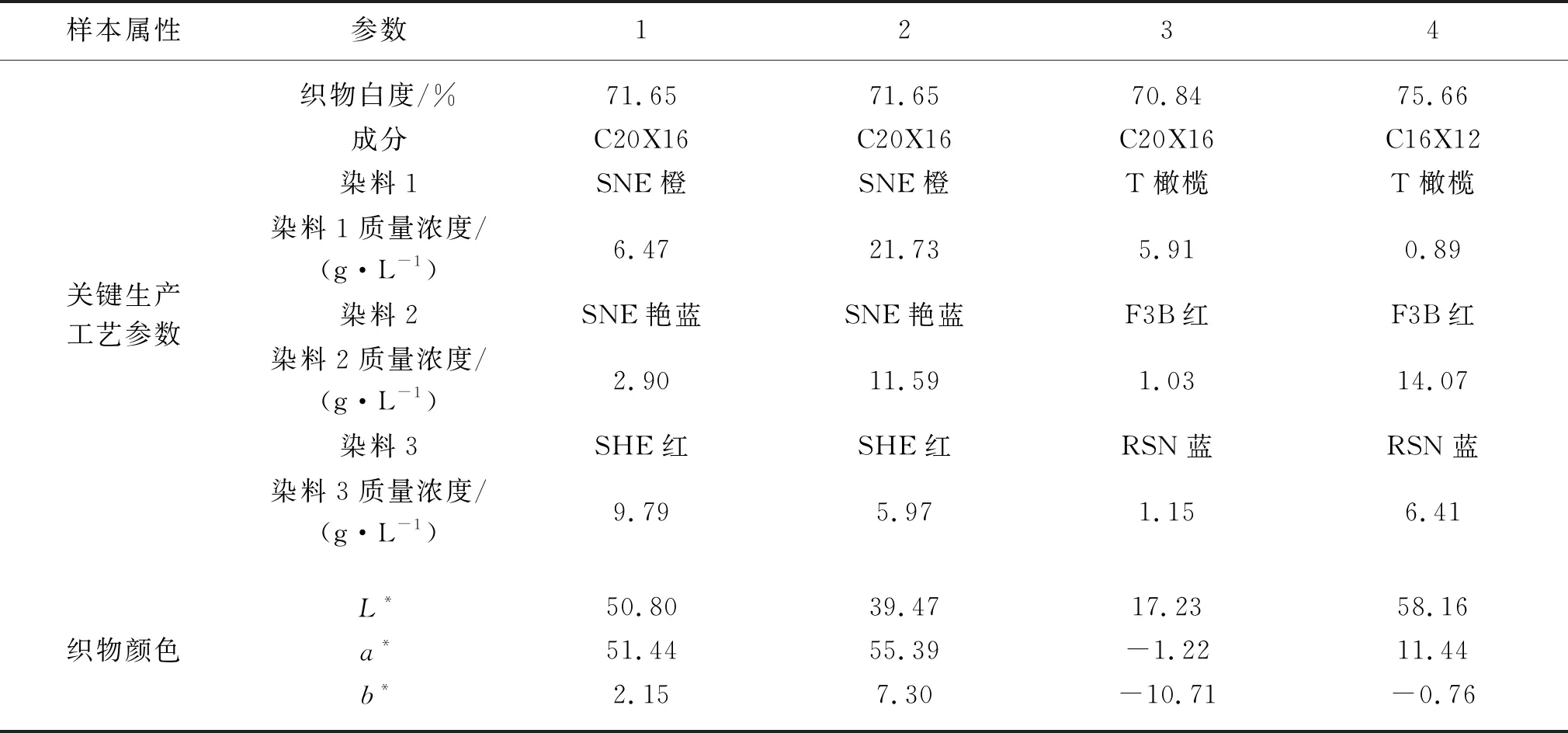
表1 部分原始数据Table 1 Partial raw data

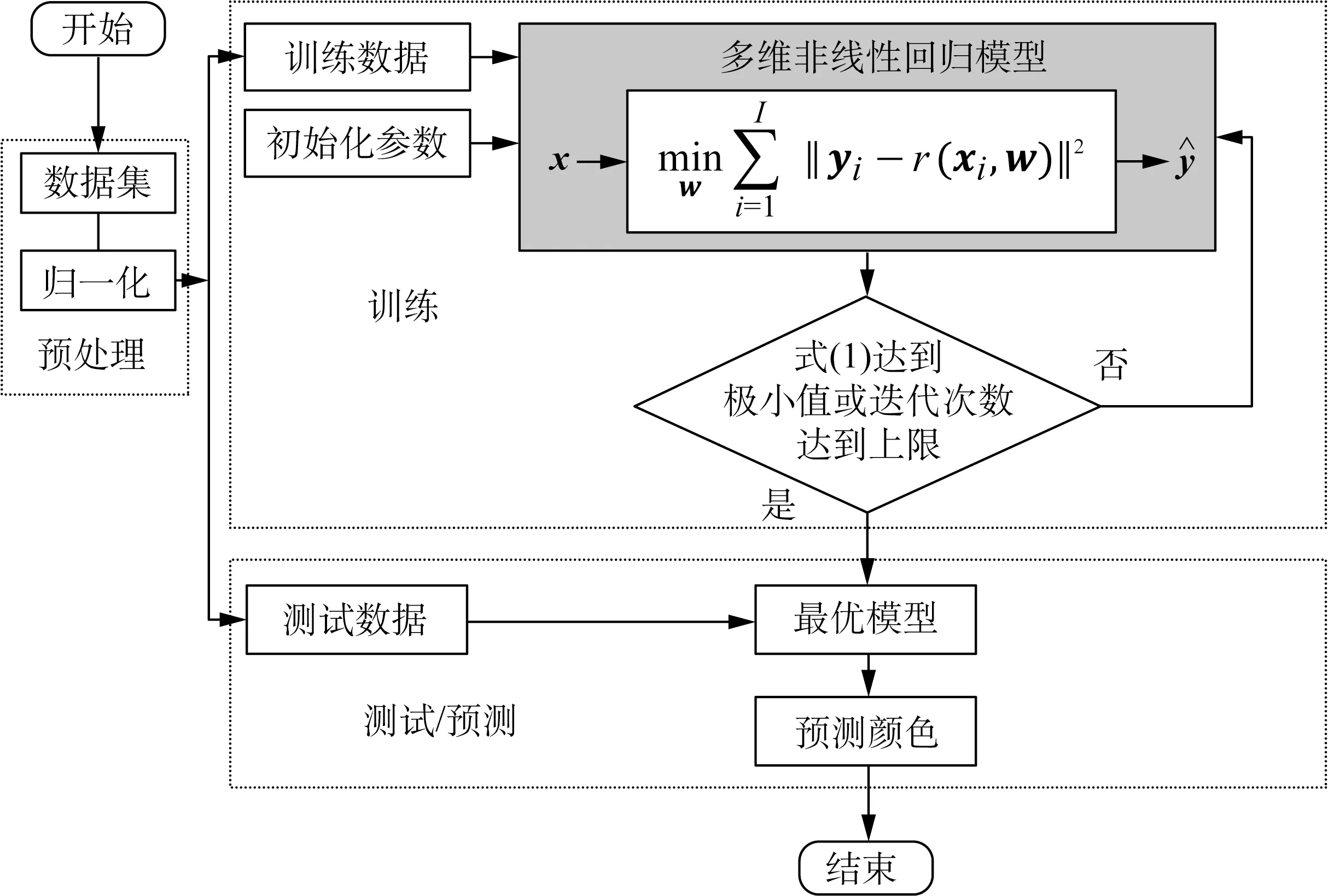
图1 织物颜色自动预测框架流程图Fig.1 Flowchart of automatic fabric color prediction framework

1.2 算法设计

为实现织物颜色预测，采用BPNN、M-SVR和GA-BPNN等3种机器学习算法估计多维非线性回归函数r(·)。

1.2.1 多元非线性回归算法

为描述实现方案的步骤，分别给出BPNN、M-SVR或GA-BPNN的设计原理。

(2)

Perez-Cruz等[10]引入核映射，提出M-SVR算法，其模型如式(3)所示。

(3)

GA模拟自然界优胜劣汰的生物进化过程，从代表问题的潜在解集的一个种群开始，以迭代的方式进行适应度计算以及选择、交叉、变异操作，从而进化种群个体，最终在末代得到最优解[11]。利用GA对BPNN的参数初始值进行优化[12]，使得BPNN经过较少的训练迭代次数就能达到预期目标，还可提升BPNN的收敛速度和织物颜色预测效率。

1.2.2 实现步骤

将多元非线性回归算法BPNN、M-SVR和GA-BPNN作为图1中的多维非线性回归模型r(·)，实现织物颜色预测。其步骤如下：

算法端到端的织物颜色自动预测算法

输入：关键生产工艺参数训练样本xi∈Rn，其对应的织物CIELAB先验值yi=[Li*,ai*,bi*]T∈Rn，关键生产工艺参数预测样本xipred∈Rn，其中n∈N*，m∈N*，i=1, 2, …,I和ipred=1, 2, …,Ipred。

//第一步 数据预处理

//第二步 训练

3) 若选择BPNN，执行步骤(4)和(5)；

6) 若选择GA-BPNN，执行步骤(7)和(8)；

9) 若选择M-SVR，执行步骤(10)和(11)；

10) 生成式(3)的参数初始值{W0,b0}；

11) 由权值迭代最小二乘法求得最优解，{W,b}代入式(3)得到多维非线性回归模型model{φ(·),W,b}；

//第三步 预测

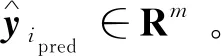
2 试 验

2.1 数据集与评价指标

试验数据来自华纺提供的轧染生产记录，经整理得到4个数据集。数据集1和2各含505个轧染小样，分别在光源D65和光源F2下通过Datacolor 650型超高精度台式分光光度测色仪测量得到其CIELAB值，数据集3包含在光源D65下实测的999个轧染小样，数据集4包含在光源F2下实测的348个轧染小样。

为实现算法中机器学习模型的训练和测试，将每组数据划分为训练集{xitrain,yitrain}(itrain=1, 2, …,Itrain)和测试集{xipred,yipred}(ipred=1, 2, …,Ipred)，其中训练集由历史染色样本的工艺参数及其所对应的先验织物CIELAB值构成，测试集由新样本的生产工艺参数及其对应的CIELAB预测参考值构成。训练样本是从每个数据集以预设比例随机挑选的，该比例称为训练样本数与样本总数之比T，按式(4)计算。

(4)

在表2所示的数据集1～4的样本容量中，改变T值(见表2第1列)，得到不同的训练集和测试集(表2第2、 3、 5、 6、 8、 9列)，然后进行相应的试验。为了定量评价颜色预测效果和模型性能，采用相关系数R、样本误差ESE以及均方误差ERMSE作为评价指标，其中：

表2 数据集1～4的样本容量Table 2 Size of data set 1 to 4

(5)

(6)

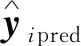
2.2 程序设置

数据集1的最优模型参数如表3所示。通过网格搜索法将不同T值下的BPNN的结构和M-SVR的参数调至最优。GA-BPNN则沿用BPNN的结构，不再进行调整。使用数据集2时，BPNN、GA-BPNN、M-SVR分别沿用数据集1的模型结构和主要参数值。BPNN的训练次数、目标误差、学习率和目标梯度分别设为10 000、10-3、0.05和10-6。M-SVR使用RBF核，目标误差为10-4，主要参数包含惩罚因子c及RBF核宽度g。GA初始化的BPNN所用的隐层层数、节点数、训练次数、目标误差、学习率和目标梯度这些重要参数都与BPNN一样。每种参数下的试验重复10次，试验结果取10次试验的平均值。为体现3个模型的预测效果，选用RBF神经网络[13]作为对比算法。所有的代码在MATLAB R2015a软件中实现，运行环境为Intel i7-6700 CPU@3.40 GHz。

表3 数据集1的最优模型参数Table 3 Optimal model parameters for data set 1

2.3 结果分析

2.3.1 织物CIELAB值预测效果

为全面评估模型的性能，在T=20%～90%条件下对数据集1～4进行试验。数据集1～4的织物颜色预测ESE均值及ERMSE值分别如表4和图2所示。

由表4和图2可知，BPNN、M-SVR、GA-BPNN都能够有效预测织物颜色，验证了算法的可行性与有效性。当训练样本较少(T=20%～30%)时，M-SVR的颜色预测误差ERMSE和ESE均值最低，优于BPNN；当训练样本较多时，BPNN则优于M-SVR。在机器学习领域，M-SVR被广泛用于小样本的数据挖掘和模式识别，而BPNN在结构上具有灵活性，其多层的结构能够更好地描述工艺参数与织物颜色之间的非线性映射关系，适用于规模较大的训练集。例如：在T=40%～90%的数据集1上，BPNN的误差较低，颜色预测效果较好。

图2 数据集1～4的织物颜色预测ERMSE值Fig.2 ERMSE of fabric color prediction for data set 1 to 4

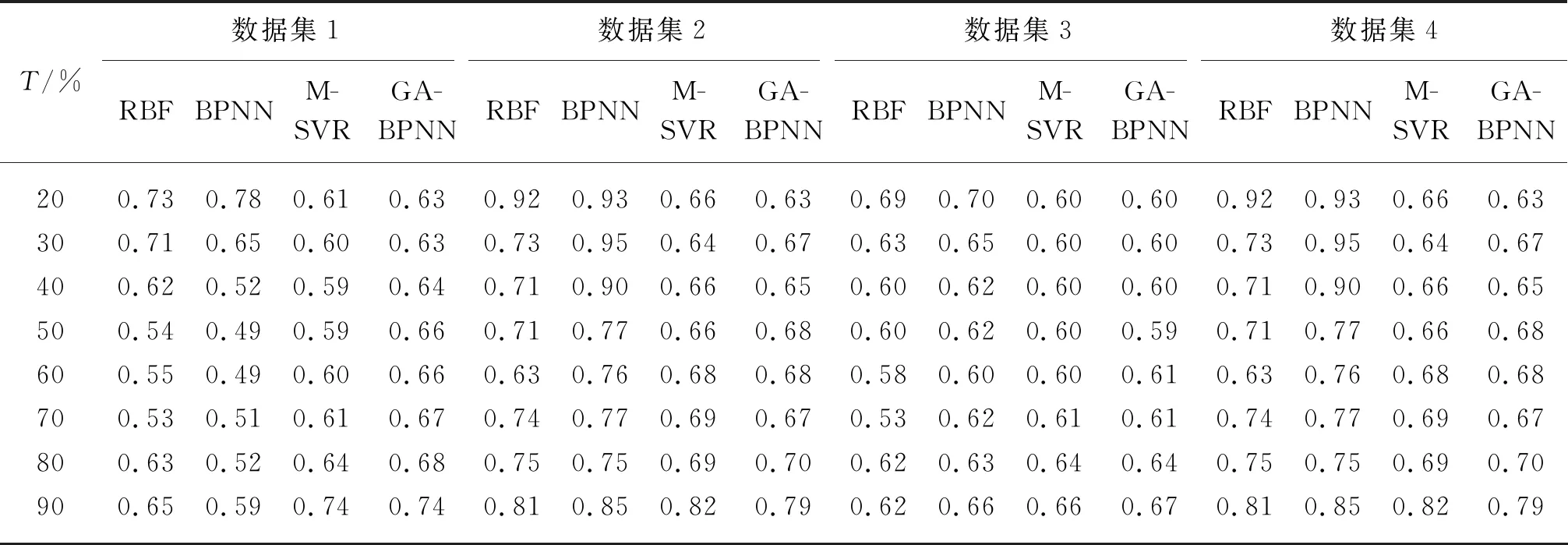
表4 数据集1～4的织物颜色预测ESE均值Table 4 Average ESE of fabric color prediction for data set 1 to 4

数据集1～4的织物颜色预测值和实际值的相关系数如表5所示。由表5可知，在相关系数方面，BPNN表现优于M-SVR，也说明BPNN的拟合性能更好。未经结构精调的GA-BPNN也能得到较低的颜色预测误差(如T=20%时，数据集1的ESE均值为0.63)，甚至低于BPNN的误差，可见GA在加快BPNN收敛速度时不会对模型预测能力造成负面影响。RBF网络的表现尚可，而BPNN、GA-BPNN、M-SVR的误差普遍小于RBF的预测误差，验证了所提端到端颜色预测框架的可行性以及本文模型的优越性和可靠性。

表5 数据集1～4的织物颜色预测值和实际值的相关系数Table 5 Correlation coefficients between predicted values and real values of fabric color for data set 1 to 4

2.3.2 织物CIELAB值预测效率

数据集1和2的训练时间如表6所示。由表6可知：数据集1中，M-SVR比BPNN运行速度更快、效率更高；数据集2中，M-SVR比BPNN更耗时，这是因为求解M-SVR最优决策面时，涉及大量矩阵运算，当训练样本数量增大时，内存开销和运行时间都会大幅攀升。由于GA-BPNN比BPNN多执行一个GA算法，因此GA-BPNN的总耗时高于BPNN。然而，在计算机运行算法并自动预测颜色之前，为保障织物颜色预测效果，BPNN需耗费大量时间执行网格搜索法以调优结构参数。将使用GA参数初始化后得到的BPNN记为BPNN(GA)。由表6可以看出，BPNN(GA)的耗时低于未使用GA的BPNN，表明基于GA的参数初始值寻优方法有助于缩短BPNN的训练时间。结合表4可知，无需精细调节结构参数，GA-BPNN也能达到较低的预测误差，表明使用GA初始化BPNN能够降低BPNN对人工调参的依赖性，节省用户在参数调节上的的时间和精力，进而提升模型的智能化、实用性以及织物颜色预测效率。

表6 数据集1和2的训练时间Table 6 Training time of data set 1 and 2

两种机器学习模型在数据集3且T为50%时的训练曲线如图3所示。当模型收敛时，说明模型已达到稳定状态，训练完毕。由图3可知：BPNN和GA-BPNN均具有良好的收敛性，能够平稳有效地实现非线性回归和织物颜色预测；GA-BPNN比BPNN收敛速度更快，收敛误差更低，说明GA能够提升BPNN的效率和效果，也印证了前文对GA-BPNN织物颜色预测性能的分析结论。收敛曲线较为平滑，说明BPNN和GA-BPNN未出现过拟合现象。

图3 BPNN和GA-BPNN的收敛曲线Fig.3 Convergence curves of BPNN and GA-BPNN

2.3.3 模型参数调优

改善模型结构、精调参数可以有力提升模型的颜色预测性能。图4给出2例网格搜索参数调优的结果。对于数据集1，当T为50%时，BPNN和M-SVR主要参数的变化对织物颜色预测ERMSE的影响分别如图4(a)和(b)所示。当BPNN的结构为8-11-8-3(P(1)/P(2)/P(3)/P(4)=8/11/8/3)，M-SVR的惩罚因子c=0.25, RBF核宽度g=0.25时，两个模型达到各自的训练样本ERMSE极小值，即最优拟合误差。由图4(a)可知，比8-11-8-3更为复杂的网络结构没有达到更低的误差，说明结构为8-11-8-3的BPNN没有对当前数据集进行过拟合。因此，对于T为50%的数据集1，选用表3中的模型参数，得到表4数据集1中的试验结果。对于其他试验，通过类似的方法，也有针对性地设计了良好的机器学习模型，实现了精确的颜色预测。

图4 T=50%时数据集1基于BPNN和M-SVR的参数分析Fig.4 Parameter analysis based on BPNN and M-SVR for data set 1 while T=50%

3 结 语

本文基于端到端的机器学习框架，将织物颜色预测问题转化为有监督的多维非线性回归问题，采用BPNN、M-SVR和GA-BPNN 3种模型进行求解，根据关键生产工艺参数预测织物的CIELAB值，并辅助提升织物配色工艺的效率。基于华纺实际生产数据的试验结果表明，所提模型能够自动有效地预测织物颜色，并且预先使用GA后BPNN的效率明显提高，说明使用GA进行参数初始值寻优的确可以缩短BPNN的耗时，从而提升其颜色预测性能。由此可见，本文研究的方法具有应用价值，可降低染色误差，减少调节染色处方的工作量。今后将研究更深层次的神经网络以及递归模型，充分利用其泛化能力和长短期记忆能力，对海量生产数据进行分析，以期进一步提高织物颜色预测的自动化和智能化。