基于MATLAB的自主水下航行器经典控制算法仿真分析

刘华栋，康宝臣，冯丽娜

（1.海军装备部，山西 太原 030027；2.山西汾西重工有限责任公司，山西 太原 030027）

0 引言

在海洋资源开发和海军军事任务双重需求的牵引下，水下无人航行器以及自主水下航行器成为当前的热门研究课题。自主水下航行器就是离开发射平台后仍具备自行航行能力至预定水域侦查、探测和打击为一体的航行器。为进一步提高布设的隐蔽性，研制自主水下航行器就显得特别重要。自主水下航行器能在敌方防潜设施外启动航行，利用其自身的动力装置航行到预定海域对敌重要港口或水域进行侦查、探测和打击。

自主水下航行器无论是在军用市场还是民用市场，全球各国都在加紧研制与开发采用最新科技成果的水下无人航行器。未来的水下无人航行器结构更加简单，功能多样，自适应能力强，可游刃有余地执行复杂的任务[1]。而各种控制算法，如神经网络控制、模糊控制、滑模控制和模糊 PID控制等智能控制算法均被应用到了UUV的运动控制中[2-7]。文献[2]采用了经典的 PID控制算法，文献[3]采用了以太网的分布式控制系统设计，文献[4]采用了滑模理论控制算法，文献[5]则将经典 PID算法、自抗扰技术、模糊策略和滑模控制算法分别进行了分析与设计，文献[6]采用了神经网络控制算法，文献[7]采用了鲁棒滑模控制算法。

进入21世纪，仿真技术得以发展的主要原因，是它所带来的巨大社会经济效益。仿真主要应用于航空、航天、航海、电力、化工以及其他工业过程控制等工程技术领域。在航空工业方面，采用仿真技术使大型客机的设计和研制周期缩短20%。利用计算机仿真，不仅节省大量燃料和经费，而且不受气象条件和场地的限制。在航天工业方面，采用仿真实验代替试航试验可使实弹试验的次数减少80%。在电力工业方面采用仿真系统对核电站进行调试、维护和排除故障，1年即可收回建造仿真系统的成本。现代仿真技术不仅应用于传统的工程领域，而且日益广泛地应用于社会、经济、生物等领域，如交通控制、城市规划、资源利用、环境污染防治、生产管理、市场预测、世界经济的分析和预测、人口控制等。因此，利用仿真技术来研究这些系统就具有更为重要的意义。

1 总体参数与流体动力参数

自主水下航行器航行控制数学模型属于灰箱系统，其运动规律遵循牛顿经典力学定律，质量守恒定律和能量守恒定律。数学模型中的流体动力参数可通过水洞试验、风动试验或自主水下航行器流体动力参数辨识得到，某航行器所需要的总体参数明细如表1所示。

表1 总体参数Table 1 General parameters

表1中：流体的密度ρ=999.866 kg/m3；航行器的体积V=1.1 m3；航行器的质量m=1 300 kg；航行器的长度L=7 m；航行器的最大横截面积S=0.224 m2；航行器质心距浮心的距离xc=-25 mm；航行器质心下移量yc=-20 mm；航行器质心侧移量zc=0；航行器绕航行器坐标系x轴转动的转动惯量Jxx=602kg·m；航行器绕航行器坐标系轴y转动的转动惯量Jyy=6 1232kg·m；航行器绕航行器坐标系轴z转动的转动惯量Jzz=6 083 kg·m2。

流体动力参数明细如表2所示。

表2 流体动力参数Table 2 Hydrodynamic parameters

2 纵向弹道数值模拟

2.1 纵向运动存在的条件

航行器在空间的运动可分解为纵向运动和侧向运动，这是一种简化的研究方法。在满足一定条件下，这种简化研究方法，在工程精度范围内是可以允许的。航行器的纵向运动为一平面运动，其运动平面与航行器的纵对称面重合，且为空间垂直平面（地面坐标系平面）。航行器纵向运动单独存在的条件是：

1）航行器对其纵对称面是对称的，在纵向运动中，不产生侧向力、偏航力矩和横滚力矩；

2）航行器控制系统是理想的，使航行器纵对称面保持在垂直面内；

3）航行器航行的弹道为垂直面内的平面弹道，如爬潜和寻深弹道，直航和垂直面导引弹道。

2.2 原始纵向运动方程组-数学模型

纵向运动是指航行器在铅垂平面（地面坐标系的ox0y0平面）内的运动，并且航行器坐标系的oxy平面与运动平面重合。纵向运动由航行器重心在oxy平面内的运动和绕oz轴的转动运动组成。由于地面坐标系的ox0轴方向可以任意选取，如果将ox0轴也选在运动平面内，则地面系的ox0y0平面，航行器系的oxy平面，速度系的ox1y1平面，半速度系的ox1y1平面都是同一平面。这时有9个运动参数，即β、υz、ωx、ωy、φ、ψ、z0、Ψ、Φc均为0，余下的非零运动参数为α、θ、Θ、ωz、υx、υy、υ、x0、y0，这9个运动参数称为纵向运动参数，描述纵向运动参数变化规律的方程称为纵向运动方程。

假定航行器具有oxy及oxz共2个对称面，于是根据航行器空间运动方程组可以得到如下方程[8]：

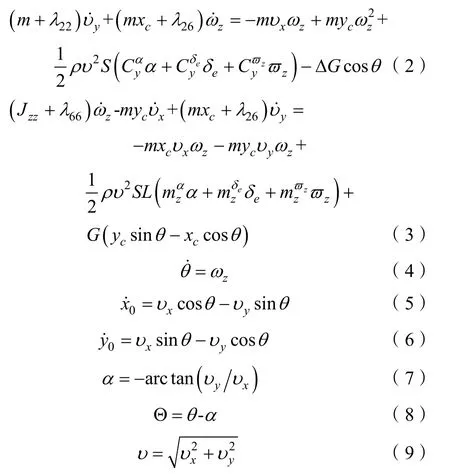
由式（1）-（9）组成的方程组就是航行器原始的纵向运动方程组。如果横舵角δe已知，则由9个方程可以求解9个运动参数，从而确定纵向运动和弹道。在固定舵角下的运动和弹道称为非操纵运动和弹道。航行器制导系统通过传感器测量航行器运动参数，通过自导系统测量目标相对运动参数，根据这些参数，制导系统给出操舵指令，形成闭环系统。制导系统的工作原理可以写成制导方程（控制方程和导引方程），在纵向运动中需要补充制导方程，与纵向运动方程联立求解纵向运动参数和横舵角δe，确定航行器运动及其弹道。

2.3 纵向运动数值模拟软件程序编制

纵向运动程序算法采用Rung_Kutta（四阶）方法，由MATLAB实现。

ODE解算器时，需要将微分方程组转化成MATLAB可接受的标准格式，如下：

ODEs由多个高阶或隐式微分方程组成，将其变换成一阶显式常微分方程组。本文的航行器纵向运动方程组是由9个隐式微分方程构成的ODEs，可转换成一阶显示微分方程，然后求解出右函数。

四阶龙格-库塔法（The Fourth-Order Runge－KuttaMethod）形式如下[9]：

航行器纵向控制方程采用如下形式[10]：

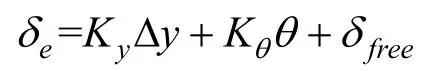
3 仿真结果

本文共进行了4种工况下的纵向运动仿真，包括稳态航速8 m/s定深5 m时的纵向运动仿真、稳态航速8 m/s定深50 m时的纵向运动仿真、稳态航速8 m/s定深5 m无自由角时的纵向运动仿真和稳态航速8 m/s定深50 m无自由角时的纵向运动仿真；由于篇幅限制，只列出稳态航速8 m/s定深50 m时的纵向运动仿真结果如下。

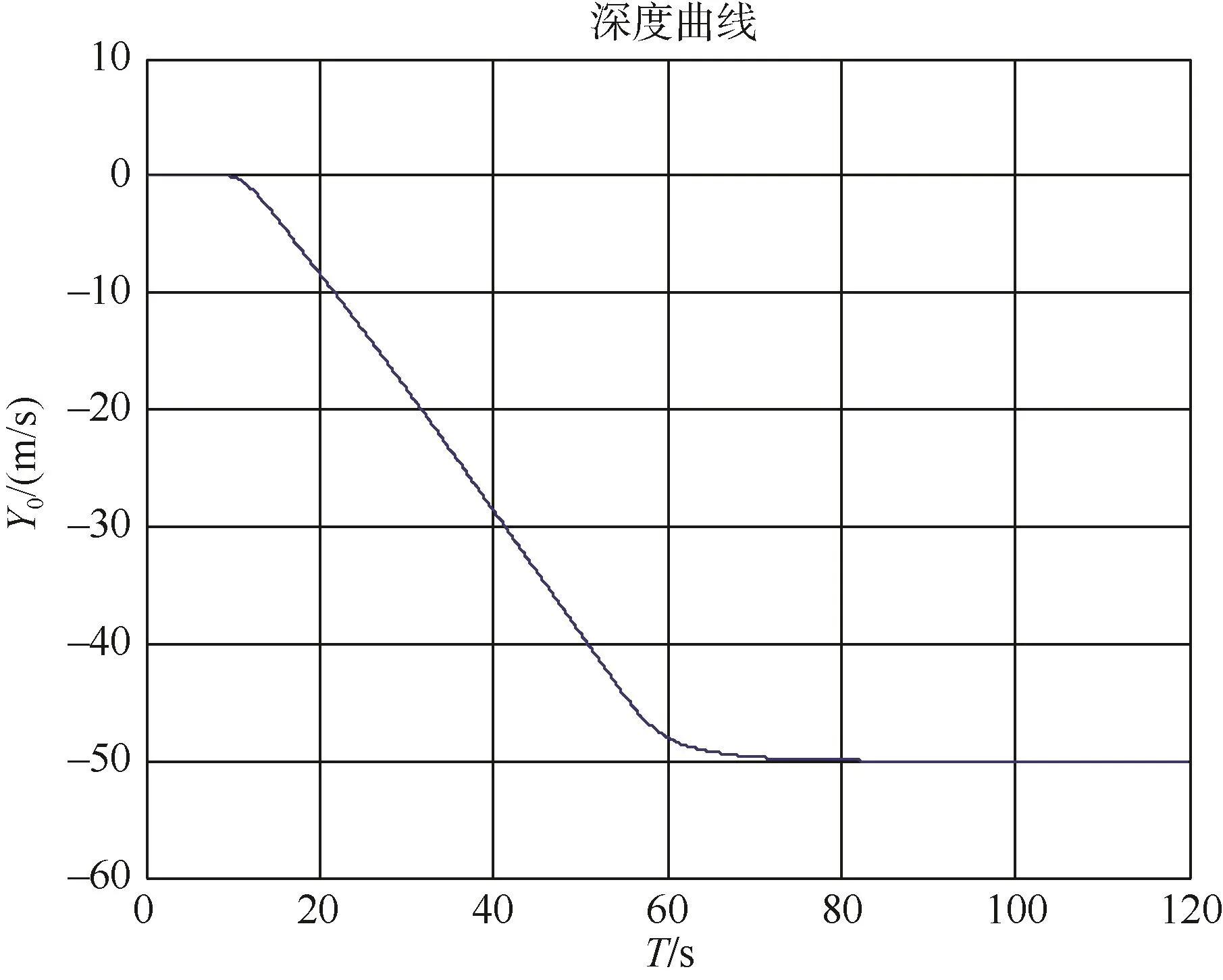
图1 深度曲线Fig.1 Depth curve

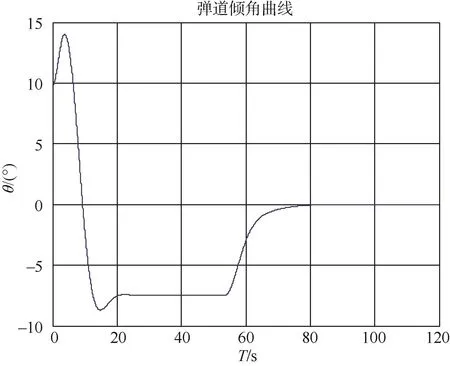
图2 弹道倾角曲线Fig.2 Trajectory inclination curve

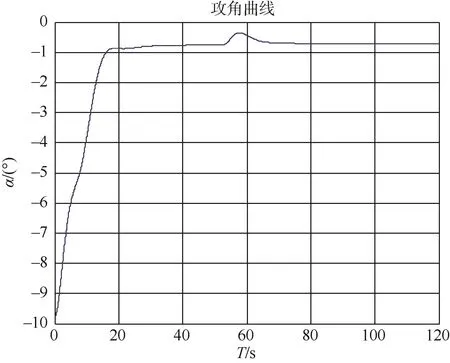
图3 攻角曲线Fig.3 Angle of attack curve

图4 弹道曲线Fig.4 Trajectory curve

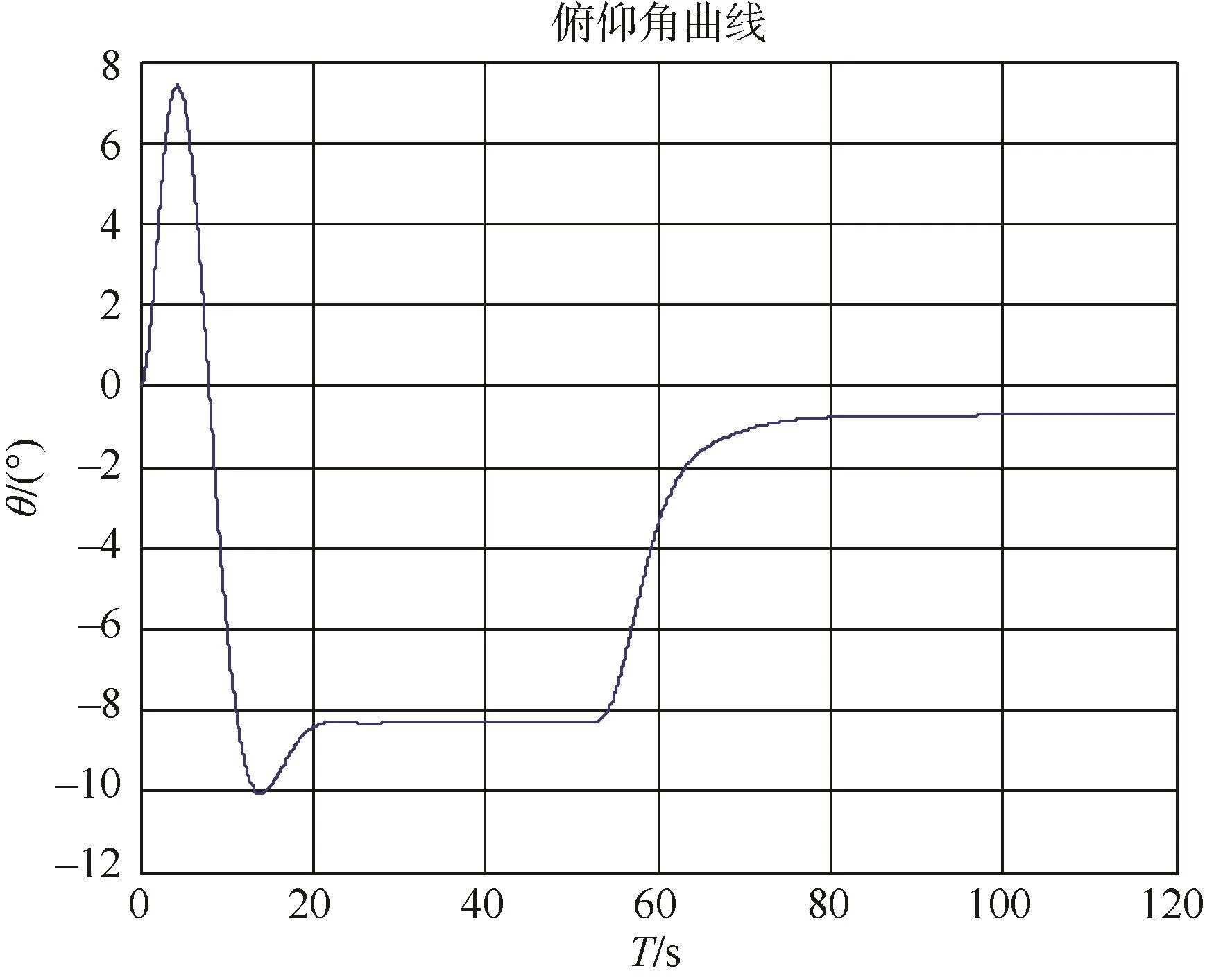
图5 俯仰角曲线Fig.5 Pitch angle curve

图6 速度曲线Fig.6 Velocity curve

图7 水平舵角曲线Fig.7 Horizontal rudder angle curve

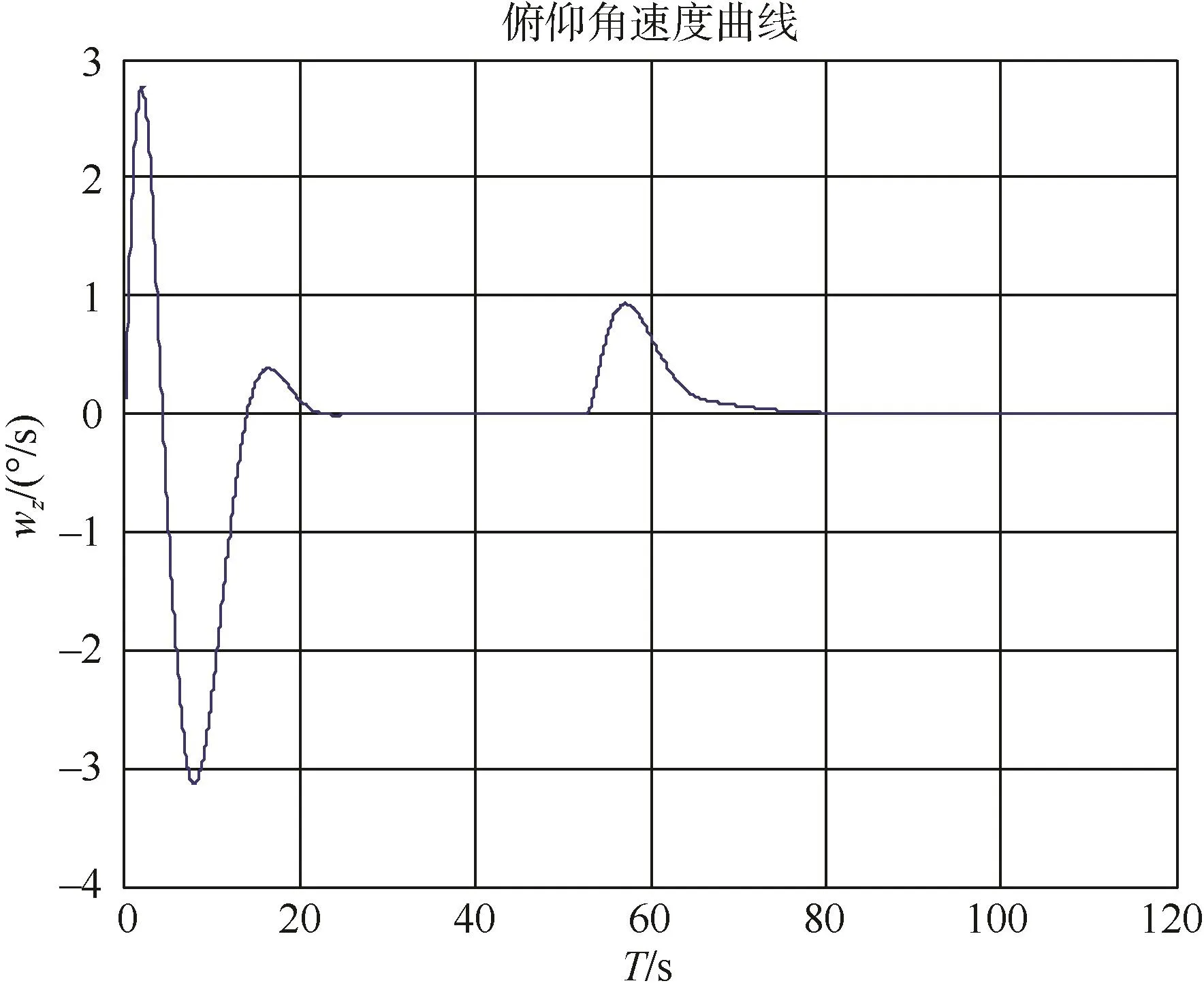
图8 俯仰角速度曲线Fig.8 Pitch angular velocity curve

通过多次仿真计算和试参数，最终确定了Ky、Kθ和δfree，并对有无自由角进行了对比，得出了自由角的取值合适时，纵向运动无超调，但稳定时间稍长，自由角偏离理想值时，纵向控制系统会产生一定的振荡和超调。

4 结束语

以上4种算例的仿真结果均给出了航行器在纵平面内的深度曲线、弹道曲线、攻角曲线、速度曲线、弹道倾角曲线、水平舵角曲线、俯仰角曲线和俯仰角速度曲线。从仿真结果可以看出：由于有重力、浮力和其它因素的影响，自主水下航行器的水平舵角不为0，而是有一个很小的度数，从而产生升力与负浮力等作用力相平衡。此外，自由角的取值合适时，纵向运动无超调，但稳定时间稍长，自由角偏离理想值时，纵向控制系统会产生一定的振荡和超调。调整好自由角的大小和传递系数就会很好地抹除此控制算法下系统产生的振荡和系统调整所耗费的时间。此仿真算例得出了合理的结果，已经验证和支持了某自主水下航行器的湖上试验，为某自主水下航行器项目实航演示样机的研制提供理论支持，具有一定的工程参考价值。