薄壁叶片侧铣变形误差补偿及刀位规划研究*

2021-05-07饶金山张而耕

制造技术与机床 2021年4期

郑刚饶金山吴雁张而耕

(上海应用技术大学机械工程学院，上海 201418)

薄壁叶片类零件，如涡轮和叶轮，被广泛应用于汽车和航空航天等领域，为保证气动性和能量转换效率，叶片常被设计成扭曲度大、几何精度高的复杂曲面，以表面为非可展直纹面的叶片类型最具代表性。对于该类叶片的加工，点铣加工方式适应度高，技术较为成熟，应用最为广泛，但点铣刀具磨损严重、效率较低，而侧铣方式，可在充分利用五轴机床灵活自由度、保证叶片表面精度的情况下，以线接触方式实现高效率的宽行切削[1]。

侧铣非可展直纹面时，由于铣刀的轴线不能被直纹面直母线上的各点法矢量同时穿过，因此存在不可避免的原理误差。原理误差的减小主要通过刀具路径规划方法实现，闫涛[2]对比两点偏置法[3]、三点偏置法[4]及优化的三点偏置法所带来的原理误差，提出以四点偏置法来生成初始刀位，并采用最小二乘进行优化，实现了刀轴矢量偏转，减小了过切误差。郑刚[5]基于双参数球族包络理论，将设计曲面离散点到刀具包络面的有向距离定义为包络误差，用序列线性规划算法使最大包络误差最小化，实现了刀具包络面朝向设计曲面的最佳一致逼近。阎长罡[6-7]以包络面逼近直纹面的整体误差出发，当特征线最小二乘逼近和映射曲线时判定单刀位位姿最优。

上述研究基于不同优化算法大大减小了原理误差，但并未考虑实际加工时叶片变形对刀位规划的影响，而工件变形误差对薄壁叶片表面质量的评估起主导作用，需要对变形误差进行必要补偿。胡自化[8]根据薄壁矩形板的有限元变形规律，利用轴线偏摆的方式进行补偿。李林[9]对侧铣非可展直纹面的铣削力进行建模，并利用有限元方法得到叶片整体弹性变形规律，根据节点变形量对设计曲面进行补偿得到待加工曲面。侯洪福[10]在铣削力模型基础上，提出以刚度矩阵的方法求解加工变形值，并基于Fanuc数控系统的原点偏置功能实现了悬臂梁工件误差的在线补偿。郑刚[11]通过在机测量的方式，根据误差补偿值调整侧铣刀位，减小了复杂曲面侧铣加工过程中的真实误差。

多数研究在原理误差的减小和加工变形误差的补偿方面做了独立深入的研究，而实际加工时，刀具沿刀具轨迹运动的每一微小距离都同时存在原理误差和加工变形，因此，综合考虑侧铣原理误差与叶片变形所带来的加工误差将更加符合实际加工情况。

1 薄壁叶片侧铣变形分析

1.1 铣削力建模

铣削力是侧铣加工过程中造成薄壁叶片变形的主要原因，现有仿真软件只能针对规则板材进行铣削力的仿真，对于复杂曲面的铣削仿真具有局限性。因此，本文采用机械力学建模的方法解决铣削力的计算问题。

根据微分思想，通过对铣削区域内参与铣削的微元进行积分得到整体铣削力，如图1。

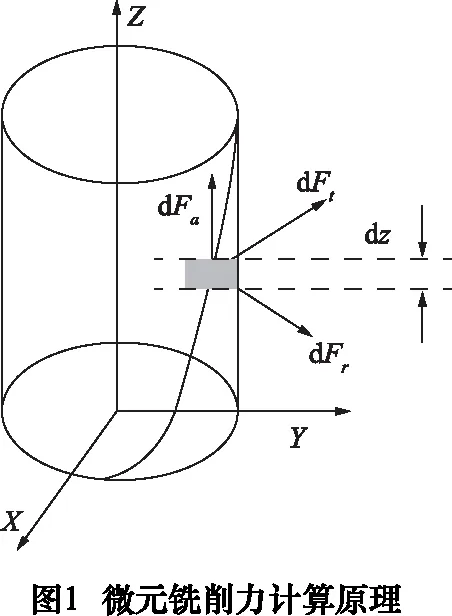
作用在高度dz上的螺旋槽切向、径向和轴向的微元铣削力表示为：

(1)

式中：fz为每齿进给量，dS为微元切削刃的长度，φj(z)为第j条切削刃在轴向高度z处的浸入角，Ktc、Krc、Kac、Kte、Krc、Kae分别为沿切向、径向、轴向的剪切力系数及犁切力系数，由铣削力正交试验进行标定。将微元切削刃上的切削力通过坐标变换，转换到刀具坐标系表示为：

(2)

根据叶片不同位置的几何参数，具体参考文献[12]中的铣削力建模方法，在MATLAB中求解出不同铣削参数组合下的铣削力。

1.2 侧铣误差预测模型

实际侧铣时，各刀位下的叶片变形量基本不同，要保证刀位误差补偿的准确性，需将刀位误差与对应刀位相匹配。初始刀位由DPO法获得：

(3)

式中：i为沿叶片切向t的刀位编号；M为刀位总个数；r(a)为扫掠体刀具的包络半径；P(t)和Q(t)是轴迹面两B样条控制曲线；piqi为刀位对应在设计曲面上的特征线，如图2。

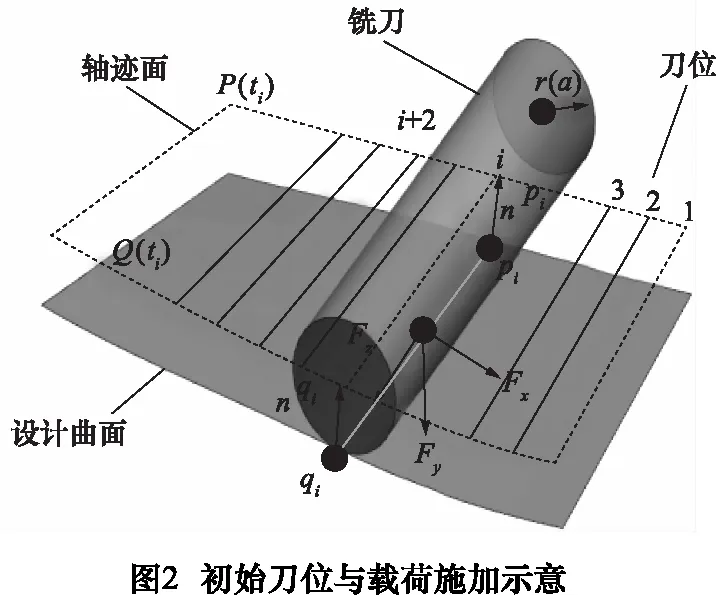
为保证误差补偿准确有效，将初始规划刀位对应的特征线作为铣削力载荷的施加位置，如图2。根据叶片几何参数计算出每个位置的铣削力分量Fx、Fy和Fz后，利用ABAQUS对连续多个刀位接触区进行有限元静态分析，获得各刀位处的弹性变形量。

2 刀位误差优化算法

2.1 侧铣刀位优化模型

根据双参数球族包络理论，侧铣加工过程可视为包络刀具沿轴迹面扫掠形成刀具包络面并向设计曲面逼近的过程，包络刀具被表示为沿轴向a扫掠而成的一系列半径可变球族，扫掠半径为r(a)：

r(a,t)=Rcosφ+‖P(t)-Q(t)‖asinφ

(4)

式中：a,t分别为轴迹面轴向及切向参数；R为锥刀底面半径；φ为刀具倾角。特别地，当φ=0时表示所用刀具为圆柱刀，刀具的包络表示方法如图3。

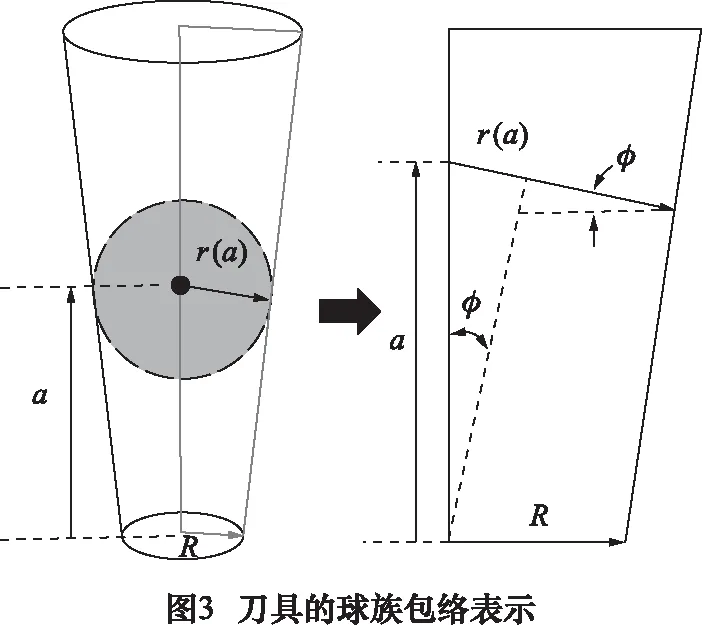
刀位规划时，原理误差为各刀位下设计曲面离散点到刀具包络面的距离。由于刀具包络面计算困难，不便表达，且最终目标是得到轴迹面的最佳引导线。因此，将设计曲面上的离散点到刀具包络面的距离转化为设计曲面离散点到轴迹面的距离，此时，点-包络面距离表示为：

(5)

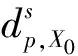
根据包络误差的性质，原理误差的减小可将点-包络面距离限制在误差允许范围内，实现刀具包络面向设计曲面离散点的最佳一致逼近，即将最大(过且或欠缺)误差最小化：

(6)

式(6)为无约束优化问题，不便求解，但可通过引入松弛变量Δ转换为可求解的有约束优化问题：

min Δ

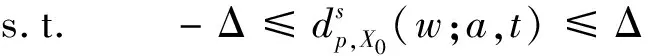
(7)

对于上述刀位整体优化模型，采用序列线性规划的方法：先将点-包络面距离在初始解处进行泰勒展开并保留线性项，然后求解近似线性规划得出新解，最后通过反复迭代线性规划所得出的新解至算法收敛，即实现整体刀位的优化，具体解法参见文献[5]。

2.2 加工误差补偿刀位的规划

在侧铣刀具规划过程中考虑叶片变形，得到误差补偿刀位，其核心要求在于保证算法精度的前提下实现刀具中心的补偿调整。

实施误差补偿的一般方法有两种：

(1)先规划刀具路径，再根据叶片变形规律，将理论刀位沿轴迹面法向实施一定的镜像补偿量以消除或减小误差。

(2)根据叶片变形规律，先对设计曲面进行误差补偿得到补偿的待加工曲面，再按刀具路径规划算法进行刀路的规划。

方法一常用于离线及在机测量后的残余误差修正，将刀位S(a,t)根据对应刀位误差δi,j进行补偿得到离散的刀位点Si,j，利用最小二乘法拟合出补偿刀位S′：

(8)

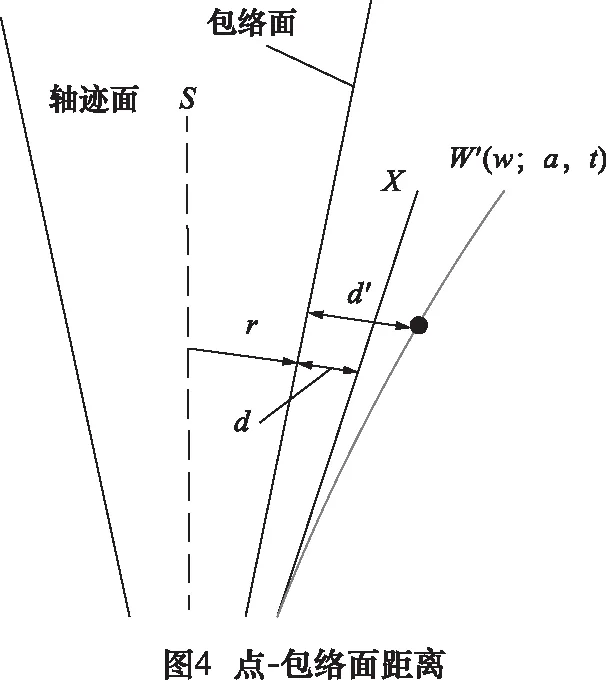
方法二中刀具截面与设计曲面的截面关系如图4所示，设计曲面为X,补偿后的设计曲面X′表示为：

(9)

式中：1≤i≤m,1≤j≤n，m,n分别为设计曲面沿a,t两向的离散点个数；Xa、Xt分别为设计曲面的轴向和切向矢量；δi,j为侧铣加工时设计曲面在a向i处和t向j处的变形误差。

根据补偿后的设计曲面，基于刀位整体优化算法，即可实现补偿刀位的规划。若以原设计曲面为参考，将变形误差作为包络误差的一部分，如图4，可不必进行设计曲面补偿面的计算。此时，考虑了变形误差的补偿，侧铣加工过程中实际点-包络面距离计算为：

(10)

以考虑变形因素的实际点到包络面距离为优化目标，采用序列线性规划算法，按图5所示算法流程，即可实现整体刀位的优化，得到补偿后的轴迹面最佳引导线。

3 叶片刀位补偿规划实例

实例采用测量得到的叶片数据，在NX下重建得到叶片模型，将叶片模型导入ABAQUS并根据实际情况赋予材料属性。为简化分析流程，在前处理时将待加工表面在t向按t=0：x：1进行参数划分，作为刀位切削力载荷的施加位置，叶片的参数划分及载荷施加位置示意如图6。

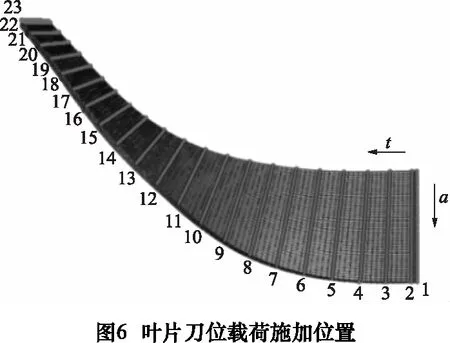
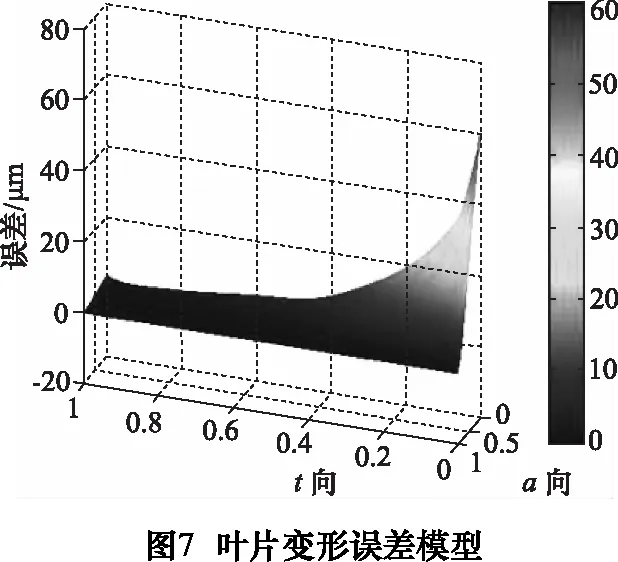
根据微元铣削力模型，在MATLAB下对图6中23个刀位进行铣削力的计算，将得到的铣削力以线载荷的方式施加在有限元单元节点上，得到各刀位处的叶片弹性变形量，按刀位规划离散方法在a、t两向进行插值，得到如图7所示的叶片整体变形误差。

采用参数为R=3,φ=0的圆柱铣刀，先进行理论刀位的规划，生成理论刀位时叶片的原理误差分布如图8。

结合图6与图7可得出：在不同刀位的铣削接触区，刀具参与铣削的轴向有效长度不同，因不同的铣削力而造成叶片各刀位下的变形量也不相同，其中，叶缘变形相对较大，最大变形发生在轴向接触最长刀位处的叶尖。

结合图7与图8可知，侧铣加工时的叶片最大变形误差为0.061 1 mm,刀位规划后残存的原理误差：最大欠切0.018 8 mm、最大过切-0.017 6 mm。变形误差相对原理误差较大，所以，对侧铣过程中的叶片变形误差进行补偿会明显改善叶片表面质量。

由方法一，根据变形误差对规划好的刀轴进行调整，得到离散的刀轴偏置点，采用最小二乘法拟合得到补偿刀位，部分刀位如图9a。

由方法二，将δi,j作为每个刀位下的加工变形误差，将刀位误差补偿至对应刀位生成二次加工曲面，按新的点-包络面距离进行刀位规划的部分刀位如图9b。

叶片刀位规划时原理误差的大小范围为-0.017 6～0.018 8 mm，叶片铣削时的变形误差范围为0～0.061 1 mm。若将补偿后的刀具包络面(待加工曲面)与原设计曲面的偏差定义为综合误差，则根据综合误差的定义，待加工曲面与设计曲面的综合误差理论上应处于-0.017 6～0.079 9 mm。利用上述两种不同补偿方法得到侧铣补偿刀位，综合误差分布及大小如图10。

根据图10，方法一所采用的最小二乘拟合离散刀位的综合误差为-0.063 1～0.132 2 mm，且最大过切发生在叶根部位，由图9a即可得到验证。叶根过切远大于理论上的偏差，在实际加工时必将在叶根处产生较大过切，降低叶片的整体刚度和寿命。方法二的补偿规划刀位的综合误差为-0.017 4～0.079 7 mm，最小偏差与原理误差中的最大过切基本保持一致，最大偏差与综合误差上限基本相等，在不影响原算法精度的前提下实现了变形误差补偿。