地下工程排水措施失效非稳定渗流效应研究

王子捷, 肖 明

(1.武汉大学水资源与水电工程科学国家重点实验室，湖北 武汉 430072；2.武汉大学水工岩石力学教育部重点实验室，湖北 武汉 430072)

在水电站地下洞室群施工及运行过程中，排水措施往往会由于渗流结晶作用、水流冲蚀作用等各种原因堵塞失效[1-2]，造成地下水位逐渐抬升，易使主要洞室群发生渗透破坏，故采用数值模拟方法对比分析排水失效前后渗流场及渗流量的变化在工程计算分析中具有重要意义。目前，基于有限单元法的排水孔模拟方法有多种，其中较为成熟的方法有空气单元法[3]、子结构法[4]、隐式复合单元法[5]等，但这些方法多数是考虑稳定渗流的情况，对于排水孔的非稳定渗流效应研究较少。此外，目前多数研究仅针对于排水失效前后地下稳定渗流场的情况，而实际上，排水措施失效过程及失效后渗流场的变化都是随时间变化的非稳定过程，仅仅采用稳定渗流分析存在一定局限性。

本文基于排水孔模拟的隐式复合单元法[5]，考虑排水孔的给水度、单位贮存量等非稳定渗流参数的等效方法，提出非稳定渗流情况下排水孔的模拟方法，同时，结合非稳定渗流的抛物型变分不等式提法[6]，探究地下渗流场在排水措施失效后随时间的变化规律。最后，采用简单的模型算例，验证方法的合理性，并探究了排水失效后地下水随时间的变化规律。

1 排水孔失效后非稳定渗流场模拟方法

1.1 非稳定渗流的抛物型变分不等式提法

由陈益峰等提出的非稳定渗流的抛物型变分不等式提法[6]，将渗流溢出边界上的Signorini型边界条件及内部自由面边界条件转化为自然边界条件，从而极大程度地改善了数值计算的收敛性及稳定性。

定义试探函数ΦPVI为

(1)

则该提法可表述为：在ΦPVI中求一随时间变化的函数φ，使对∀ψ∈ΦPVI，都有：

(2)

上述即为非稳定渗流的抛物型变分不等式提法。

1.2 排水孔模拟的复合单元法

岩土材料的渗透特性一般是各向异性且非均匀的，而排水孔的渗透特征亦不同于岩体，它们的渗透系数、给水度、单位贮存量也各不相同，此时可用复合单元法来确定单元的渗流参数[5]。

排水孔可视为内含在岩体中的空气单元，而空气可以视作一种强透水介质。当排水孔内含在岩体单元或穿过岩体单元时，则可将其视为岩体单元中的一个子域，此时包含排水孔的岩体单元就成为了复合单元。

在模型进行离散，建立模型网格时，首先建立不考虑排水孔的整体有限元网格。模型网格建成后，再组织排水孔的起、终点单元号、坐标、直径等信息数据。在后续数值计算中，只需根据实体单元与排水孔之间的关系，修正包含排水孔或有排水孔穿越的实体单元的渗透传导矩阵及单位贮存量、给水度等参数，这样就可以实现对排水孔的数值模拟。在该方法中，排水孔隐含于岩体中，只需建立整体有限元网格，而不需要对排水孔进行实际单元模拟。故该方法有建模简单，便于应用的优点。

由于排水孔的强排水作用，沿其轴向的渗透性显著增强，垂直于轴向一定范围的渗透性也有所加强，因此排水孔的走向与倾角会造成单元的渗透传导矩阵有所不同。此时可将排水孔视做空间圆柱体，求出其轴向方向向量即为其主渗透方向(见图1)。假定沿排水孔轴向向下为其局部坐标系x′轴，其x′轴向主渗系数为kx′。为便于计算，令ky′的主渗透方向取在局部坐标系x′轴与整体坐标系y轴所形成的平面内，可以求出y′轴的方向向量。取x′轴与y′轴的方向向量叉积为z′轴的方向向量。

图1 排水孔渗透方向示意图

如图2所示的单元体内，有两根排水孔穿过，排水孔A与单元表面交点为2，排水孔B与单元表面的交点为1和3。根据其交点结合排水孔设计求出其轴向渗透系数kx′A及kx′B，将其平移至相交的平面内叠加得到等效排水孔的渗透系数kx′(如图3)。同理，也可以得到另外两个方向的渗透系数ky′和kz′。

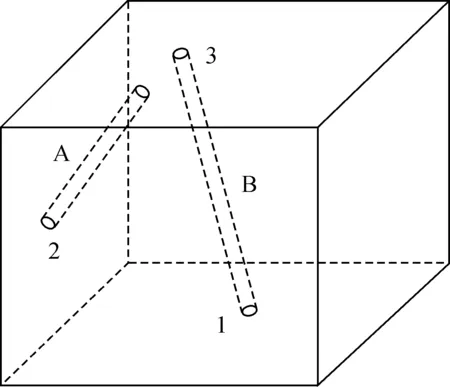
图2 单元内排水孔位置示意图

图3 多排水孔空间向量叠加图

考虑每个排水孔在复合单元中的状态，对单元内的所有排水孔进行等效，然后计算得到每个主渗透系数与坐标轴之间的方向余弦lx，ly，lz，组成坐标转换矩阵[Rp]：

(3)

则可在整体坐标下得到排水孔的等效传导矩阵：

[Kp]=[Rp]T[K′][Rp]

(4)

式中，[Kp]为排水孔的等效渗透张量。

根据单元渗透传导矩阵计算原理，可将含排水孔复合单元的渗透传导矩阵表示为：

(5)

式中：[A]为复合单元渗透传导矩阵；vp为单元内排水孔所占体积；vr为岩体体积。

将含排水孔复合单元视作一个整体，设其等效渗透矩阵为[Kd]，则整个复合单元的渗透传导矩阵又可以表示为：

(6)

联立式(5)、(6)，则可以求得复合单元的等效渗透传导矩阵。

在非稳定渗流计算中，除了渗透系数之外，还需考虑复合单元单位贮存量及给水度的等效。

对于单位贮存量Ss而言，根据其定义，可以认为其是各项同性参数。在工程实际中，排水孔一般不承担贮水的作用，可以认为其正常工作时单位贮存量为0。由此，可直接采用体积等效的形式获取复合单元整体的单位贮存量取值。如图2所示的复合单元，所有排水孔在单元内的体积vp，单元内岩体体积为vr，单元体积为v，则有：

vr=v-vp

(7)

Ssrvr+Sspvp=Ssdv

(8)

式(8)中：Ssr、Ssp分别为岩体及排水孔的单位贮存量；Ssd为复合单元等效的单位贮存量。

求解式(8)，即可获得复合单元的等效贮水率。

对于如图4所示有自由面穿越的复合单元，还需求取其等效给水度。

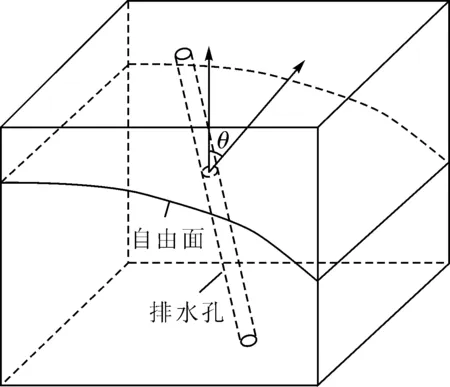
图4 有自由面穿越的复合单元示意图

对于该单元体而言，将复合单元视作整体，其系数矩阵中与给水度有关的元素可记为：

(9)

将排水孔和岩体分开，复合单元的自由面边界的系数矩阵中的元素又可写成：

(10)

(11)

联立式(10)、(11)即可求取有自由面穿越的复合单元的等效给水度。

1.3 排水孔逐渐失效过程模拟

排水系统在实际运行中，由于结晶作用，会随着运行时间增长逐渐堵塞失效，其是一个涉及到温度、pH、CO2、排水孔内水流流速等多种因素影响的一个复杂过程，其堵塞失效的规律及其何时完全失效亟需系统性研究，本文为简化计算，将排水孔由于结晶作用逐渐堵塞失效的过程视为排水孔孔径随时间增加匀速减小的过程，即排水孔的截面积及体积不断减小，当孔径减小到0时，排水孔即等效于岩体，此时视为排水完全失效。其具体计算形式如下：

(12)

式中：D0为排水孔正常运作时的孔径；T0为假定的排水孔完全失效的时间；t为已运行时长；Δt为非稳定渗流计算的时间步长。

结合其他勘测资料及边界信息，首先采用稳定渗流方法获取有排水措施情况下的地下渗流场分布，再以此为非稳定渗流计算的初始条件，随时间变化逐渐改变排水孔的孔径大小，探究排水逐渐失效后地下渗流场的变化规律，具体流程见图5。

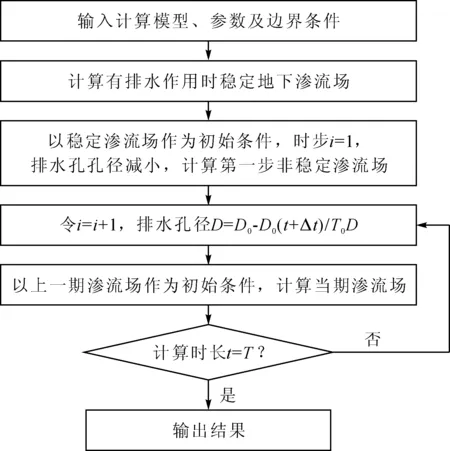
图5 排水措施失效过程非稳定渗流计算流程图

2 算例分析

2.1 计算模型及计算参数

为探究排水孔失效后渗流场变化规律，设置一个含排水孔的地下厂房简化模型。模型范围为250 m×250 m×250 m(x×y×z)，主厂房的尺寸为30 m×80 m×50 m(长×宽×高)，厂房底部距模型底部60 m，位于研究区域正中心，排水孔布置在厂房周围，间距5 m，直径80 mm，距离厂房边界20 m，顶部排水孔呈45°斜向上。研究范围内整体有限元模型及厂房、排水孔布置见图6及图7。

图6 整体有限元模型图

图7 地下厂房及隐式排水孔布置图

计算条件设置如下：研究区域岩体的渗透系数取为1.0×10-7m/s，给水度取0.1，单位贮存量取1.0×10-6m-1，排水孔等效渗流参数按文献[7]中建议取值。沿x方向左右两侧设置为定水位边界，水位均为200 m，模型底面及沿y方向前后两侧面取为隔水边界，主厂房洞室边界取为潜在溢出型边界，排水孔按前文所述的复合单元法进行模拟。

计算首先考虑排水孔正常作用的情况，然后以此情况下的计算结果作为初始条件，并假定排水系统在运行的第30 d后完全失效，按式(12)模拟其逐渐失效的过程，研究排水孔失效过程中地下渗流场的变化规律、主厂房渗流量的变化情况，并预测渗流场达到最危险情况的时间。

非稳定渗流计算的总时长取为2个月，计算时步长取为2 d。

2.2 结果分析

不同时刻渗流场计算结果如图8所示。当地下厂房处于完备渗控措施作用下时(t=0)，地下水自由面有效降低，地下水渗漏点仅出现在厂房底部，说明复合单元法能有效体现排水孔列阵的排水功能。当排水孔逐渐失效后，自由面逐渐升高，且水位变化呈现出前期抬升速度较快、后期抬升速度较慢的规律，这是由于渗透压力在前期排水孔失效过程中变化较大。在排水孔逐渐失效过程中，由于其孔径减小，复合单元的渗流参数不断变化，导致渗流场变化较大。30 d后，排水措施完全失效，此时渗流场虽未达到稳定状态，但此时包含排水孔的复合单元已视为普通的岩体单元进行计算，渗流参数不再改变，渗流场的变化只是随着时间的增加逐渐趋于稳定状态。对于具体时刻的渗流场变化而言，在失效14 d后，地下水将排水系统及主厂房全部淹没。当到达第54 d后，自由面趋于稳定，不再变化。此时，自由面最低位置高出厂房顶拱50多米，厂房处于极其危险的状态，在实际工程中应尽量避免排水孔完全失效情况的发生。

图8 排水失效后渗流自由面变化图

图9为厂房洞壁渗流量随时间变化示意图。由图可知，当排水孔完全生效时(0 d时)，主厂房渗流量仅有30.4 m3/d，渗流量较小，厂房运行安全。当排水孔逐渐失效后，主厂房渗流量变化规律与自由面变化规律相一致，在前期迅速增加，一段时间之后趋于稳定。地下水稳定后，主厂房渗流量达到152.3 m3/d，是排水孔完全生效时的5倍多，极易发生渗透破坏，说明排水措施对厂房安全运行起到至关重要的作用。

总体而言，本文提出的方法能够体现出排水失效后地下水非稳定变化规律，能为后续的工程实际计算提供一定参考。

图9 厂房渗流量随时间变化图

3 结 语

本文基于非稳定渗流的抛物型变分不等式法及排水孔模拟的隐式复合单元法，提出排水孔模拟的非稳定渗流方法，并考虑了排水孔逐渐失效的过程，结合一个简易的地下厂房模型探究了排水措施失效后地下水的非稳定渗流规律，可得到以下结论：①在排水系统逐渐失效的过程中，地下水自由面迅速升高，呈现出前期升高速度快、后期升高速度慢的规律，最后趋于稳定；②渗流量变化规律与自由面变化规律相近，达到稳定后厂房流量大小是有排水时的5倍，实际工程中应尽量避免排水失效情况的发生。