区域坐标转换模型对比分析

王 萌，高 远，范咪娜

(山东正元数字城市建设有限公司，山东 烟台 264670)

北斗卫星导航系统(BDS)于2020年成功组成完整星座系统，标志着BDS在全球范围内具有了定位能力、在中国范围内具有了高精度定位能力[1-3]。GPS系统使用的坐标系统为WGS-84系统，而我国组建的BDS系统的坐标系统为CGCS2000[4-6]。随着BDS的逐步普及，全国范围内的CGCS2000的建立就显得尤为关键[7-10]。我国使用的1980西安坐标系统将逐渐被CGCS2000取代，各地区已经开展了相关的坐标系统转换工作；由于卫星定位系统的坐标系统由WGS-84转化为了CGCS2000，因此也需要在这两种坐标系之间进行转换，以获得某些控制点的CGCS2000坐标值以提供静态定位的初始值[11-12]。

区域坐标系统转换有多种数学模型，布尔莎四参数是最为常见、计算最为简单的模型，随着测区增大也可以增加为七参数[13-14]。四参数转换模型属于相似变化模型，不同坐标系间的差别主要取决于两个方面：坐标系定位、定向、椭球参数及尺度因子；局部误差和累积误差，其中局部误差属于变形误差，累积误差来自测量控制网[15-16]。仿射六参数模型在布尔莎四参数的基础上增加了两坐标轴的尺度因子，由于存在坐标轴尺度因子使此种模型在布尔莎四参数的基础上更为灵活[17-18]。多项式逼近模型是一种数学逼近模型，与坐标转换原理无关，根据参数数量只要提供足够的已知点数据，即可进行预测，此方法的优点是可以摒弃坐标系统本身的系统误差对坐标转换原理的误差影响，得到更优的计算结果。但在一些高精度的已知坐标转换中，可能无法获得高精度的转换结果[19-20]。

本文以四川某区域施工坐标系与CGCS2000的转换工作为例，通过平面四参数模型、仿射六参数模型和多项式逼近模型的计算，探讨此区域坐标转换中的最佳计算方法，为建立CGCS2000提供经验。

1 转换模型

1.1 平面四参数模型

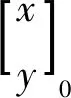
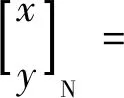
(1)

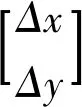
令(1+m)Δx=a，(1+m)Δy=b，(1+m)cosα=c，(1+m)sinα=d，式(1)可简化为：

(2)

由以上原理，只需要2个已知点，即可利用最小二乘法建立超定方程组求最小二乘解。

1.2 仿射六参数模型

仿射六参数坐标转换公式见式(3)：

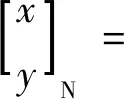
(3)

式中，mx和my分别为两坐标轴的尺度因子。

利用最小二乘法进行解算，至少需要3个已知点，将其化简为相关的6个参数，称其为仿射六参数模型。若只需要进行坐标转换，可在求出6个参数后直接进行转换而不需求出原始的5个因子。与平面四参数模型类似，可以通过式(2)的方法简化计算。

令(1+mx)Δx=a1，(1+mx)cosα=a2，(1+mx)sinα=a3，(1+my)Δy=b1，-(1+my)sinα=b2，(1+my)cosα=b3，式(3)可化简为：

(4)

1.3 多项式逼近模型

多项式逼近模型如式(5)和式(6)所示：

(5)

(6)

式中，α0，α1，…，α5、β0，β1，…，β5为多项式系数；(xk，yk)0是变换中心附近一个点的坐标。

2 实例计算

本次实例计算选用四川某城市控制网坐标，已知数据如表1所示。特别说明，由于坐标原始数据比较重要，表中坐标值已经经过一定程度的变换，非原始坐标。评价计算结果时，以计算值和真值的差作为残差。

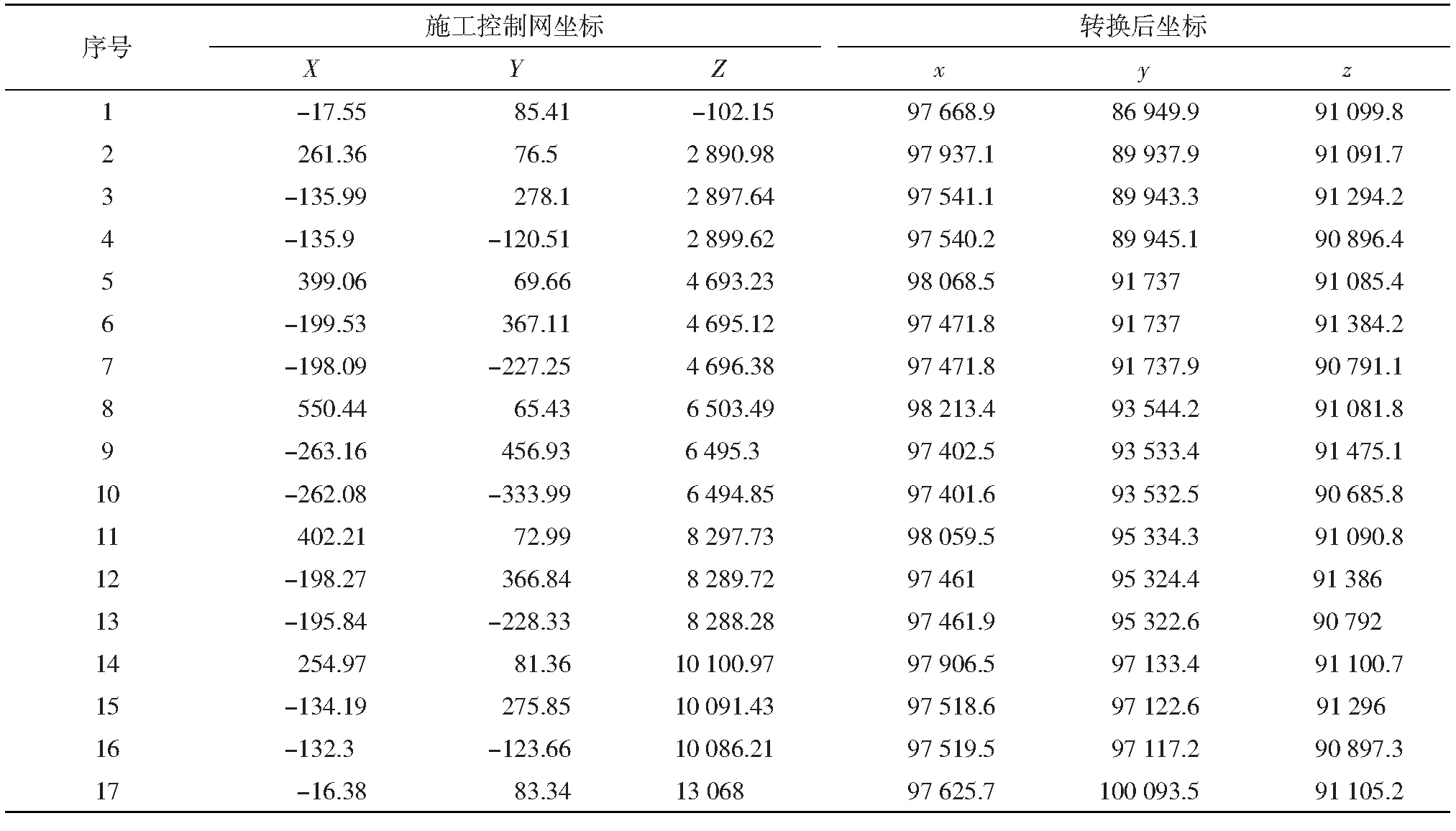
表1 已知数据/m

2.1 平面四参数模型计算

将式(2)改写误差方程，如式(7)所示：

V=BX-L

(7)

求式(7)的最小二乘解，公式如式(8)所示：

X=(BTB)-1BTL

(8)

2.2 仿射六参数模型计算

2.3 多项式逼近模型计算

将式(5)改写误差方程，如式(7)。式中，V为改正数；

将式(6)改写误差方程，如式(7)。式中，V为改正数；

3 计算结果分析

将平面四参数模型、仿射六参数模型和多项式逼近模型计算残差绘制折线图，如图1～图2所示。

为更为详细地评价三种模型的计算精度，引入观测值的中误差这一精度评价方法，其公式见式(9)：

(9)

式中，m为观测值的中误差；v为误差；[]为求和符号；n为观测次数。

计算三种模型的X坐标与Y坐标的中误差，如表2所示。

表2 中误差/m

由图1可以看出，平面四参数转换后X坐标精度不高，出现了一些残差达到±0.7～±0.8 m的坐标点，X坐标中误差为0.468 m；仿射六参数X坐标精度较低，出现了一些残差达到-0.95～0.95 m的坐标点，X坐标中误差为0.451 m；多项式逼近X坐标精度很高，残差集中在-0.3～0.3 m之间，X坐标中误差为0.138 m。

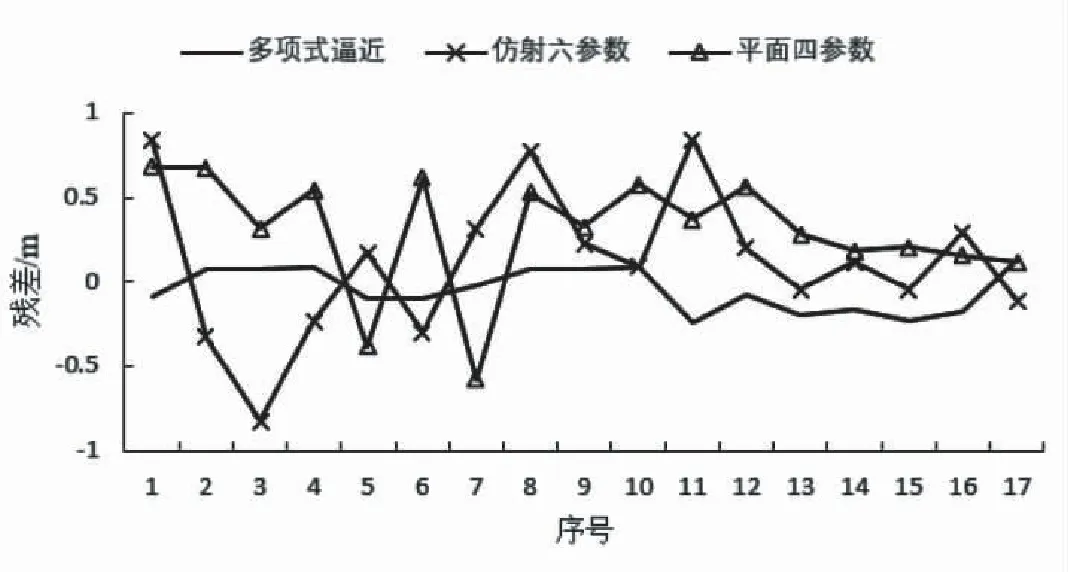
图1 X坐标误差

由图2可以看出，平面四参数转换后Y坐标精度不高，出现了一些残差达到0.7～0.8 m的坐标点，但负值范围内精度尚可，Y坐标中误差为0.408 m；仿射六参数Y坐标精度不高，出现了一些残差达到-0.5～0.95 m的坐标点，Y坐标中误差为0.435 m；多项式逼近转换后Y坐标精度很高，残差集中在-0.2～0.2 m之间，Y坐标中误差为0.106 m。

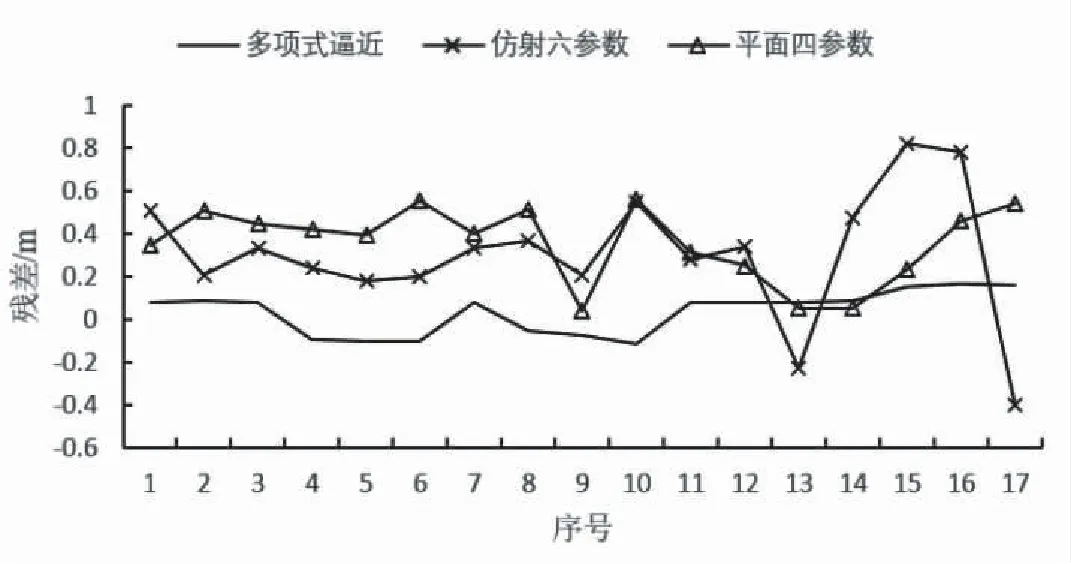
图2 Y坐标误差

三种模型计算结果的残差值如表3所示。

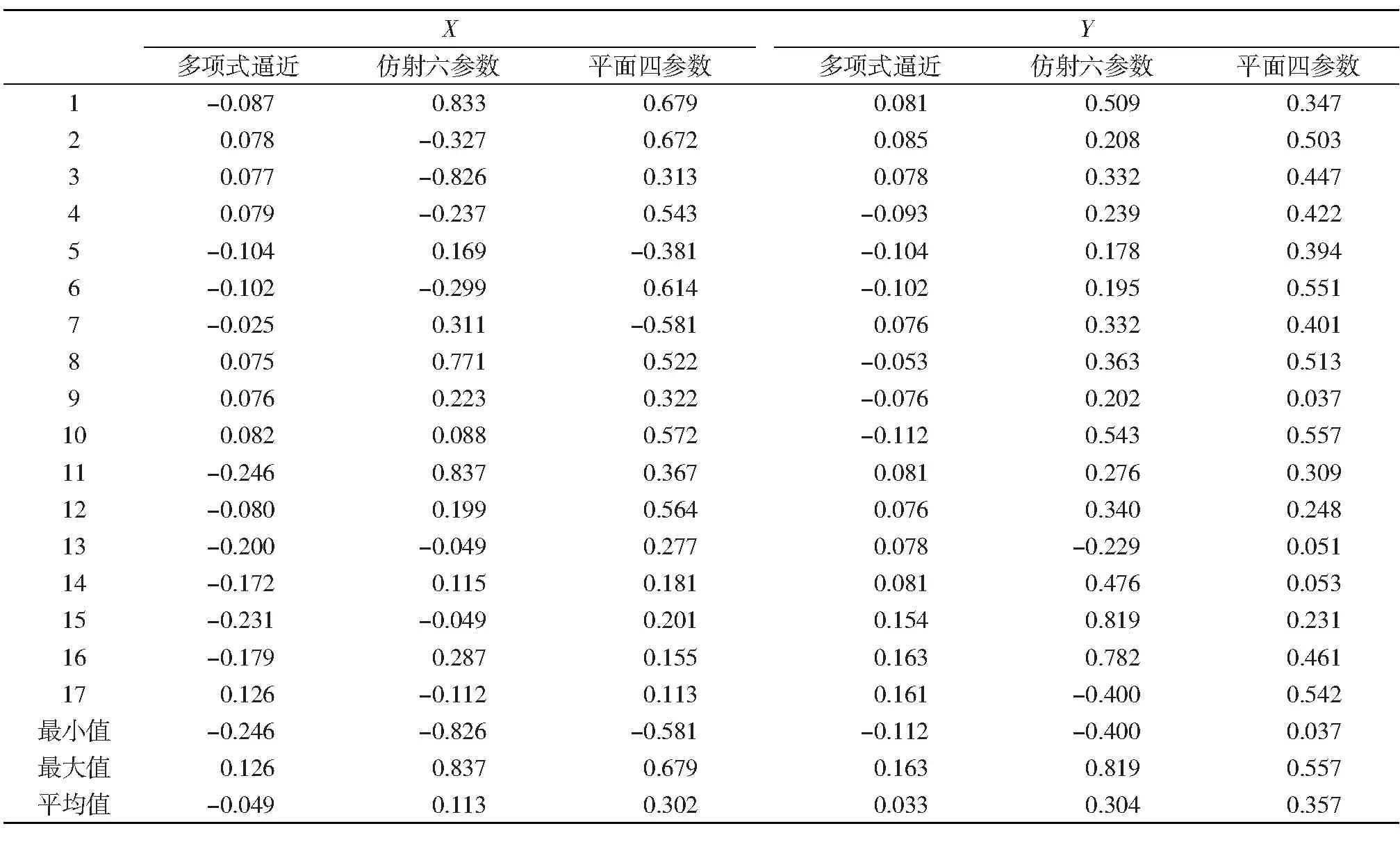
表3 三种模型计算残差对比/mm

由表3可知，平面四参数模型计算X坐标残差最小值为-0.581 m，最大值为0.679 m；Y坐标残差最小值为0.037 m，最大值为0.557 m；仿射六参数模型计算X坐标残差最小值为-0.826 m，最大值为0.837 m；Y坐标残差最小值为-0.400 m，最大值为0.819 m；多项式逼近模型计算X坐标残差最小值为-0.246 m，最大值为0.126 m；Y坐标残差最小值为-0.112 m，最大值为0.163 m。综合三种模型计算的残差图、残差表、中误差、最大最小值，多项式逼近模型精度较高，残差大多维持在厘米级，转换后的坐标值可以用于实际工程测量中。

4 结 论

本文以四川某区域施工坐标系与CGCS2000的转换工作为例，通过平面四参数模型、仿射六参数模型和多项式逼近模型的计算，探讨此区域坐标转换中的最佳计算方法。通过实例计算发现，平面四参数和仿射六参数模型计算精度较低，原因是原始转换坐标为施工控制网坐标，建立时不够精确，会带有一定的系统误差，而平面四参数和仿射六参数均为按照坐标转换原理推导的数学模型，因此在该区域坐标转换中效果较差；多项式逼近模型是一种纯数学模型，可以更好地避免系统误差，得到较好的区域坐标转换效果。

为进一步提高坐标转换精度，下一步工作可尝试对模型拟合点与检核点的方案进行讨论，在已知点中选取若干拟合点进行模型预测，使用检核点评价模型精度，以确定该区域坐标转换的最优拟合点分布。