本是同根生——浅谈正弦定理与余弦定理的关系

安徽省界首市界首中学 袁 梦

阜阳市教科所王志刚副所长在一次教研活动中说：“正弦定理和余弦定理的本质是一样的。”这引起了笔者的极大兴趣。经过一段时间的思考和研究，笔者认为正弦定理和余弦定理是“本是同根生”的关系。下面将从以下几方面来加以说明，如有不当之处，请批评指正。

一、三角形边角之间的关系

我们可以按照章建跃博士的整体建构理论（研究对象是谁？构成要素是什么？要素与要素之间的关系有哪些？）对三角形进行重新建构，会发现三角形是由三条线段组成的一个封闭图形；它的构成要素是三条边和三个角。那么，要素与要素之间的关系有哪些？

1.边与边的关系

（1）直角三角形：两直角边的平方和等于斜边的平方（勾股定理）。

（2）一般三角形：两边之和大于第三边，两边之差小于第三边。

2.角与角的关系

（1）直角三角形：两个锐角度数之和等于直角。

（2）一般三角形：三个内角之和等于180o（内角和定理）。

3.边角之间的关系

（1）直角三角形：锐角的正弦等于对边长除以斜边长，锐角的余弦等于邻边长除以斜边长。

（2）一般三角形：我们可以类比直角三角形中边角关系归纳猜想出正弦定理：在一个三角形中，各边和它所对角的正弦的比相等，由直角三角形中的勾股定理可以猜想出余弦定理：对于任意三角形，任何一边的平方等于其他两边的平方和减去这两边与它们夹角的余弦的积的两倍。

从以上的发现过程和结果来看，正弦定理和余弦定理都是反映三角形边角之间的关系，是三角形中的内隐关系，就像内角和定理一样。所以它们是同根生的关系，其本质是一样的。

二、我中有你，你中有我

在三角形中有一个重要的结论：在△ABC，角A，B，C 所对的边分别为a，b，c，则a=b cosC+c cosB。

1.由正弦定理推导余弦定理

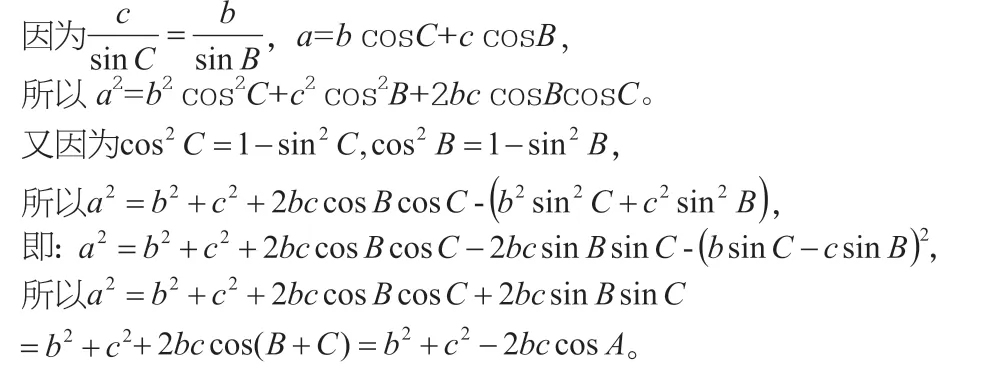
同理可证：

2.由余弦定理推导正弦定理

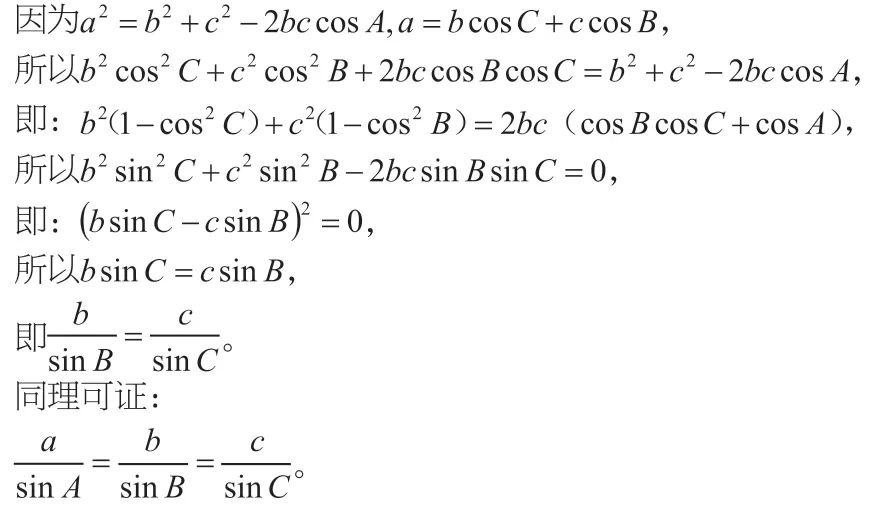
三、两定理能解决的公共问题

从解方程的角度可以清楚地知道利用正弦定理可以解决以下解三角形问题：

（1）已知三角形的两角与任一边，求其他的边和角；

（2）已知三角形的两边与其中一边的对角，求其他的边和角。利用余弦定理可以解决以下解三角形问题：

（1）已知三角形的两边与其夹角，求其他的边和角；

（2）已知三角形的三边，求其他的边和角；

（3）已知三角形的两边与其中一边的对角，求其他的边和角。

显然，这个问题“已知三角形的两边与其中一边的对角，求其他的边和角”是两定理都可以解决的。但在解决这个问题时，无论用哪个定理求解都要注意是否有解？有几个解？

四、教研感悟

1.专家引领促青年教师快速成长

一个学校要想有较好的发展，就必须有一批业务精湛的教师，然而事实是，很多学校别说有一批，就算有几个也算不错了，在这种情况下，导致很多青年教师成长缓慢。还好现在网络发达，线上教研已成常态，如果学校或个人不能借助“专家的资源”，就会错过绝好的发展机会。本人通过这次王志刚所长在教研群里的引领，就有了对解三角形内容的更深刻的理解，有豁然开朗的感觉。所以一个学校或一个地区的青年教师要想快速成长，就应该主动请专家指导。

2.各显神通，教学相长

我把此次教研经历和学生分享，并让学生进行正弦定理和余弦定理的互相证明，结果学生表现出了和平时不一样的积极性，最后在我们共同的努力下有了一次奇妙之旅，更有了教学相长的快乐，在不知不觉中渗透了数学运算，提升了核心素养。通过探讨正弦定理和余弦定理的关系去发现数学的本质，只有发现本质，才会觉得数学有意思，才会觉得学数学有意义，才会利用数学解决实际问题。