基于一个不等式的分析与推广

陕西省西安市经开第三中学 韩文乐

一、基础理论知识预备

回看2019 年的高考数学全国统一卷，我们发现对于不等式的考查，从最初的简单的直接求解，到近几年具有巧妙思维的求解，考题越来越趋向灵活性，考查的重点从要求考生会求解，到要求考生灵活运用，不等式的求解也越来越趋向于对基础知识的拓展，考查学生的逻辑思维及知识拓展能力。

高中阶段对不等式的求解一般参考不等式的缩放技巧，不等式的缩放是高考考查重点知识。常见的缩放技巧有以下几种：（1）“添舍”放缩，针对不等式的一边进行添项或者减项。（2）放缩分式，根据已知，若分式的分子变大，则分式值相应变大，若分母变大，则相应的分式值变小。一个真分式，分子、分母同时加上同一个正数，则分式值变大，可达到证题目的。（3）裂项放缩，如果不等式含有与自然数n 有关的n 项和，那么可采用数列中裂项求和等方法来解题。（4）公式放缩，利用已知的公式或恒不等式，把欲证不等式变形后再放缩，进行求解。（5）换元放缩，针对不等式的某个部分进行换元，即可发现问题的本质。（6）单调函数放缩，根据题目特点，通过构造相应的特殊单调函数，利用函数的单调性质进行放缩求解……本文中借助2019 年高考的一个不等式特例，对它进行了分析与求解，进而通过纵向（次数升高）和横向（参数增加）推广讨论，得出一个一般不等式，这个一般不等式对其他类似不等式的求解具有参考意义。

二、几类特殊不等式的基本解法

1.一般基础不等式

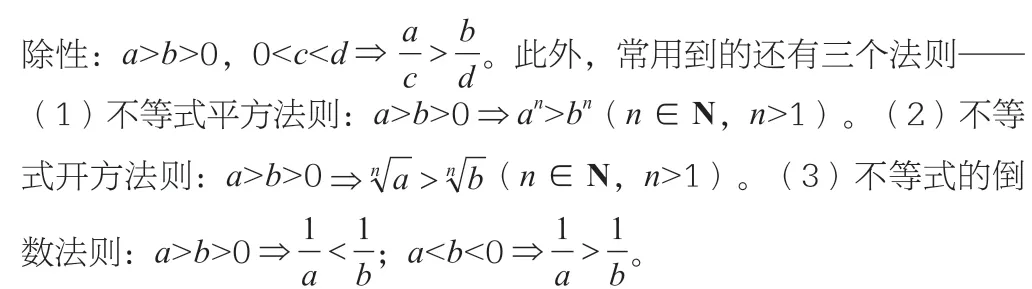
2.常见的几个重要不等式

不等式的求解最能考查学生的思维能力以及知识变通能力。这部分的题型纷繁多样，各具特点，学生在看到题时，第一时间会感到困惑，无从下手。学生除了熟悉不等式法则以外，还得积累更多的题型，掌握出题人的套路，做到举一反三。以下我们总结几种常见的重要的不等式的求解技巧：

3.几种常用的著名不等式

（1）出现频率较高的“平均不等式”：

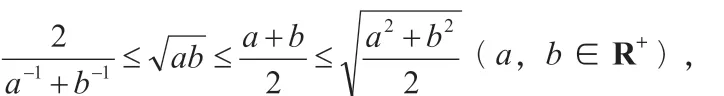
其中当且仅当a=b 时取“=”号。

简而言之，即调和平均≤几何平均≤算术平均≤平方平均。

上述式可变形为：

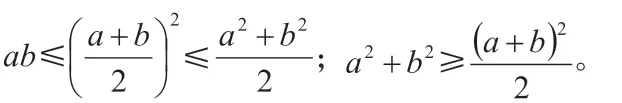
（2）有关“幂”平均的不等式：

不难看出，不等式的求解对拓展思维的提升要求较高，学生在思考的同时可以结合不等式的缩放技巧，有针对性地分析问题，也可结合数学中的归纳方法，归纳总结求证问题。本文对于不等式的证明与分析，从纵向（次数升高）和横向（参数增加）两个方面进行推广，此类求解方法对同类不等式的解决有着重要的参考作用。