高速电主轴转子-轴承系统动力学特性分析
2021-05-07贾伟涛
高 峰, 贾伟涛, 李 艳
(1.西安理工大学 教育部数控机床及机械制造装备集成重点实验室, 陕西 西安 710048;2.西安理工大学 陕西省制造装备重点实验室, 陕西 西安 710048)
高速加工是一种先进制造技术,广泛应用于航空航天、模具等高端装备制造业,极大地提高了生产率和加工精度,降低了生产成本[1]。电主轴作为高速数控机床核心部件,将原动力-传动装置-执行器-控制系统集成为一体,实现高速运行。主轴单元是影响电主轴系统稳定性的关键部件,轴承刚度对电主轴转子-轴承系统动态特性有着重要影响[2-5]。
文献[6-7]建立了考虑预紧的高速角接触球轴承动力学模型,以7012/CD轴承为例,分析预紧对高速角接触球轴承动态刚度的影响。Zhang等[8-10]建立了角接触球轴承在不同预紧机制下的刚度分析模型。结果表明:在固定位置预载荷作用下,该轴承具有较好的刚度稳定性。采用时程图、相图和Poincaré图分析了不同支承下,转子轴承系统的动力学特性,结果表明,系统的动态特性随轴承刚度及转速的变化呈现出倍周期、准周期和混沌运动特性,可用于预测转子轴承系统的动力学响应[11-14]。文献[15-18]建立不同支承下高速转子系统的非线性模型,通过求解Floquet乘子矩阵的对数确定原系统的稳定性,并得到系统稳定极限曲线。基于稳定性理论[19],给出了二维动力系统在不动点处的局部稳定性[20-21]。高速旋转电主轴,由于质量偏心诱发的离心力是主要的激励源之一[22-23]。由于电主轴轴径较小,出厂前又做了很好的动平衡,因而很多学者[24-25]在进行动力学分析时,通常忽略轴系离心力对主轴系统动力学特性的影响。实际上在高转速状态下,轴系离心力的影响是客观存在的。Wang等[26]研究了高速电主轴系统在离心力和轴承刚度软化效应下的动态性能。结果表明:上述因素对电主轴的动态性能影响较大。
考虑离心力及轴承刚度软化效应,以150MD25Z7.5电主轴为研究对象,建立电主轴转子-轴承系统的非线性动力学模型,分析不同运行参数下,电主轴系统动力学响应,并讨论了动力系统不动点处的局部稳定性。
1 动力学模型
高速电主轴由转子、定子、转轴、前后支承轴承、壳体等基本机械部件组成。图1为高速电主轴的基本结构形式,转子和定子置于主轴前后轴承之间。
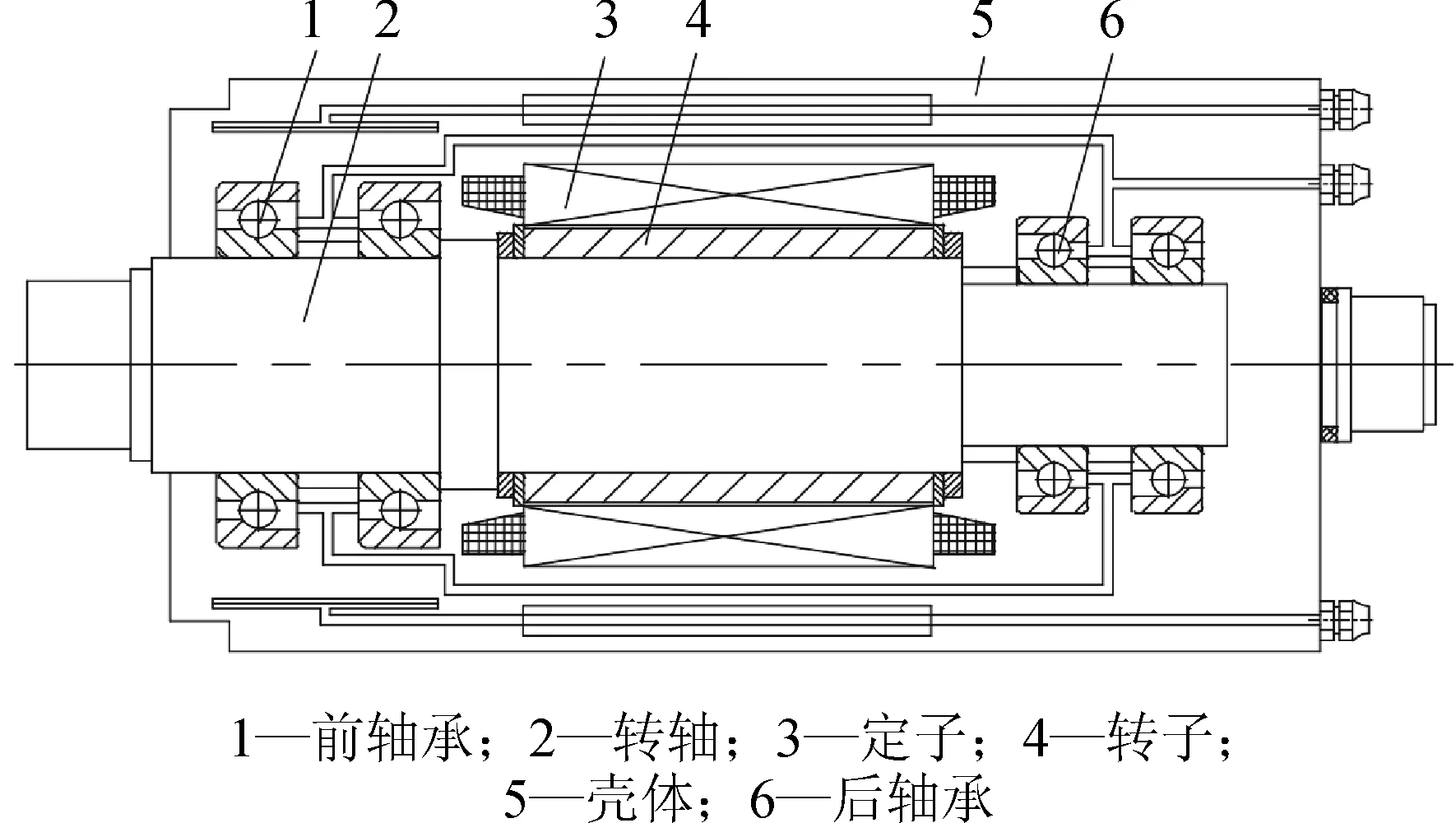
图1 电主轴结构简图
对于高速电主轴,根据其转子系统的结构特点,将其简化为包含质量不平衡的转子-轴承系统模型,见图2。其中,S为圆盘几何中心,G为圆盘质量中心,e为偏心距。模型中转子两端由角接触球轴承B7008支承,转轴长为310 mm,转轴质量为3.699 kg。
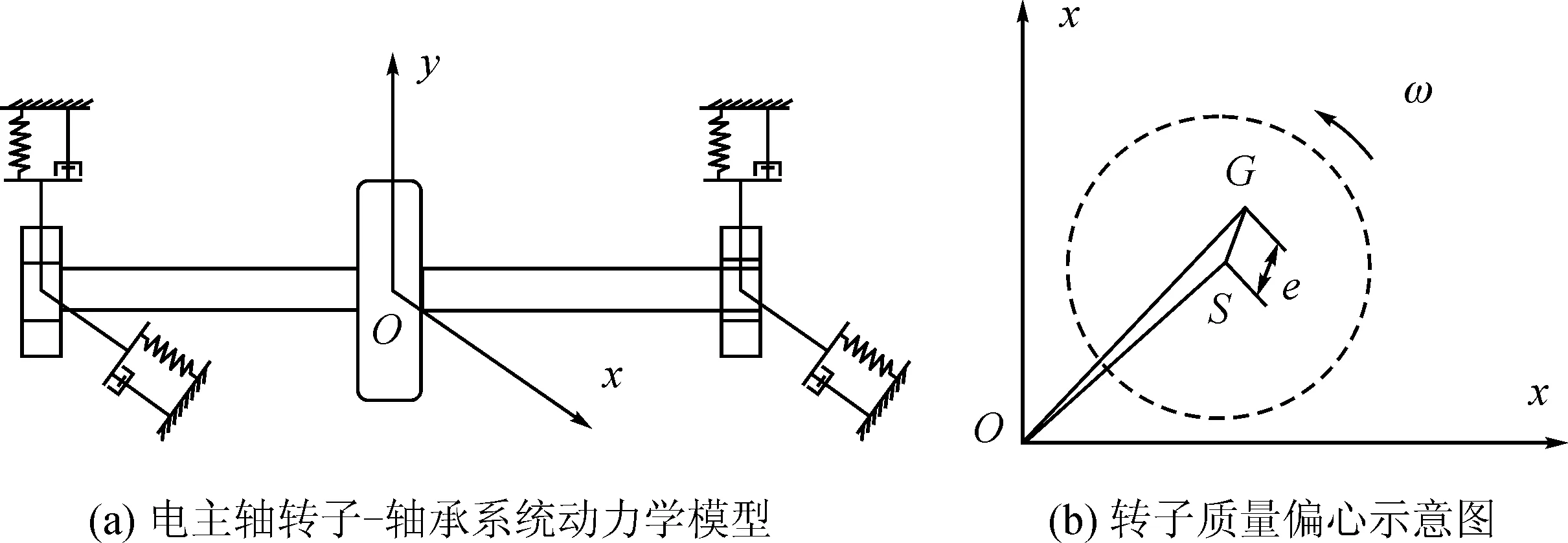
图2 角接触球轴承支承下不平衡转子动力学模型
角接触球轴承的径向刚度k1可近似按下式计算[27]:
(1)
式中:z为滚动体数目;Db为滚动体直径;α为轴承接触角;F0为轴承预紧力。
计算可得:k1=2.248 8×109N/m。
利用等效弹簧和阻尼建立具有非线性支承的电主轴转子轴承模型。在不平衡质量激励下,电主轴转子-轴承系统的运动方程如下:
(2)
式中:m,e和ω分别是转子的质量、质量偏心率和转速;c,k1和k3分别代表转子支承的阻尼、线性和非线性刚度。
由于式(2)中无耦合项,平面y的振动与平面x的振动相同,只是存在一个相位差,所以本文只研究一个方向上的振动状态。
高速磨削主轴系统是一种机电耦合系统,由于系统存在电磁刚度,转子-轴承系统表现出软特性。将式(2)写为:
(3)
式中:ξ=c/m,=|k3|/m。
将式(3)改写为:
(4)
式中:
λ=ω/ωn;ωn表示固有频率。
对于高速磨削电主轴的转子-轴承系统,r≪1,f≪1,所以将r,f认为是小参数。
2 结果与讨论
采用数值分析法求解系统动力学方程,分析电主轴转子-轴承系统动力学行为。
2.1 不同转速下的响应(k1=2.248 8×109 N/m)
轴承刚度为k1=2.248 8×109N/m,以ω作为控制参数,系统时程图、Poincaré图分别见图3~6。
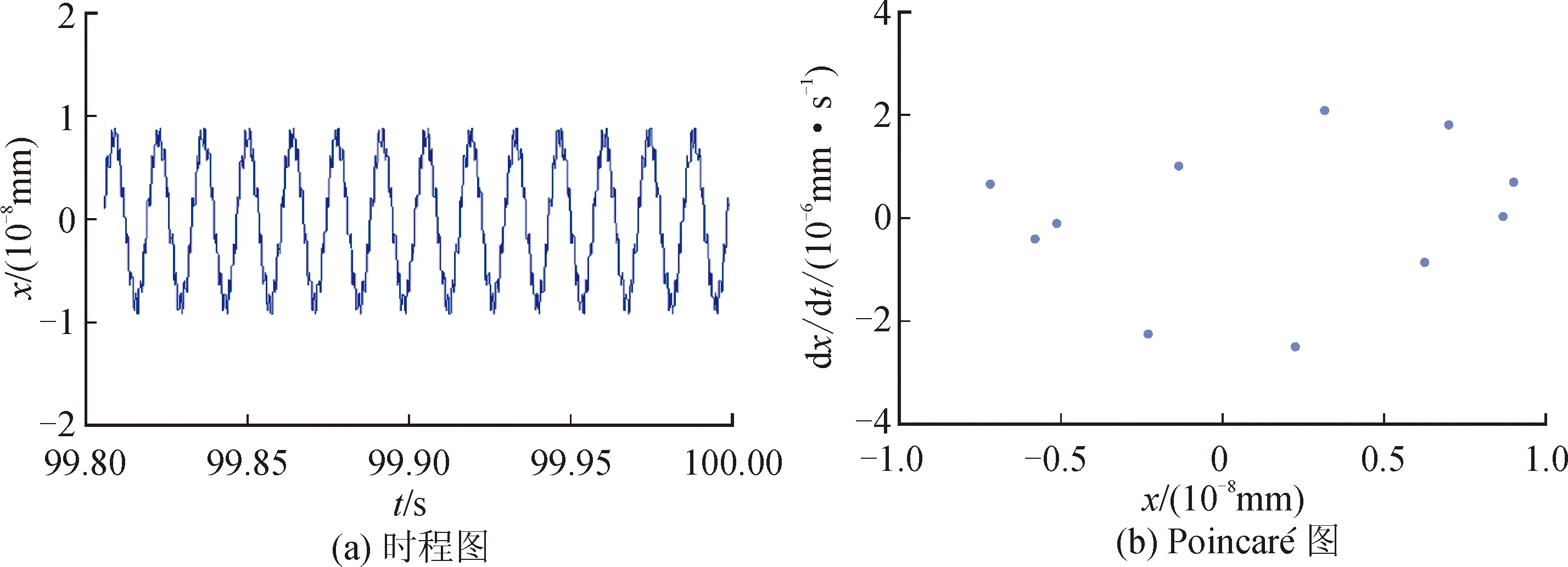
图3 转速ω=5 000 r/min时的系统响应
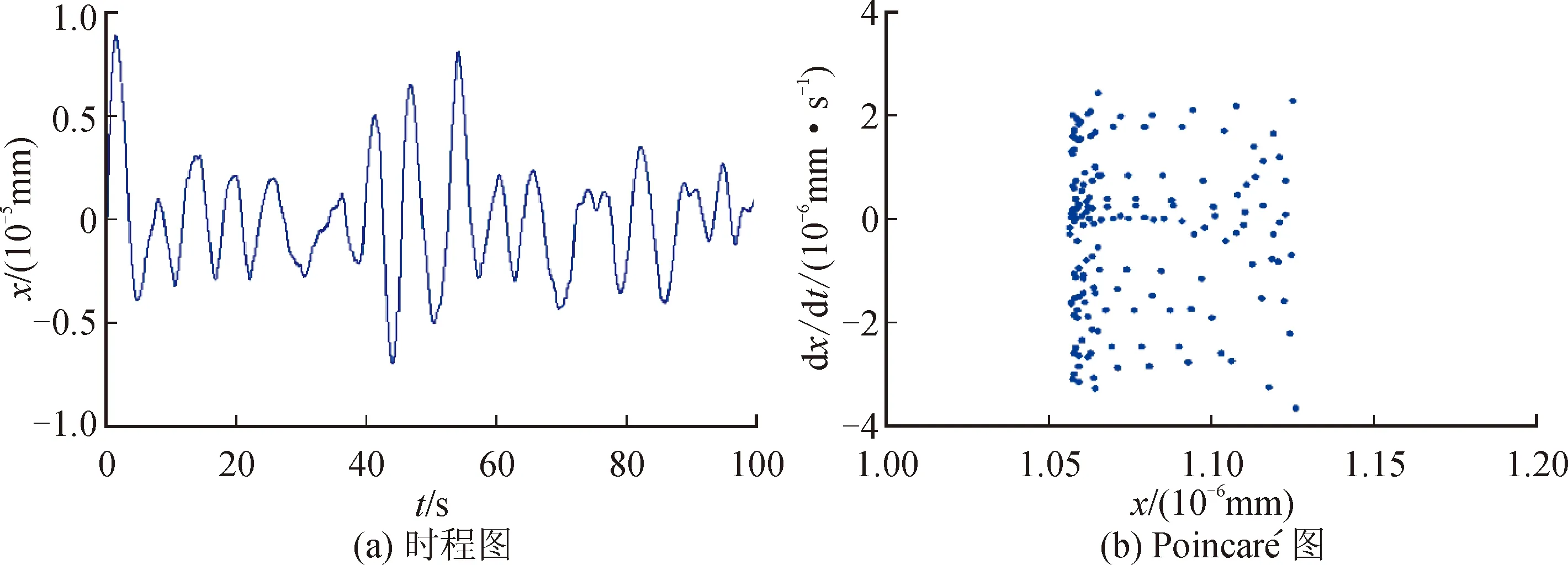
图4 转速ω=10 000 r/min时的系统响应
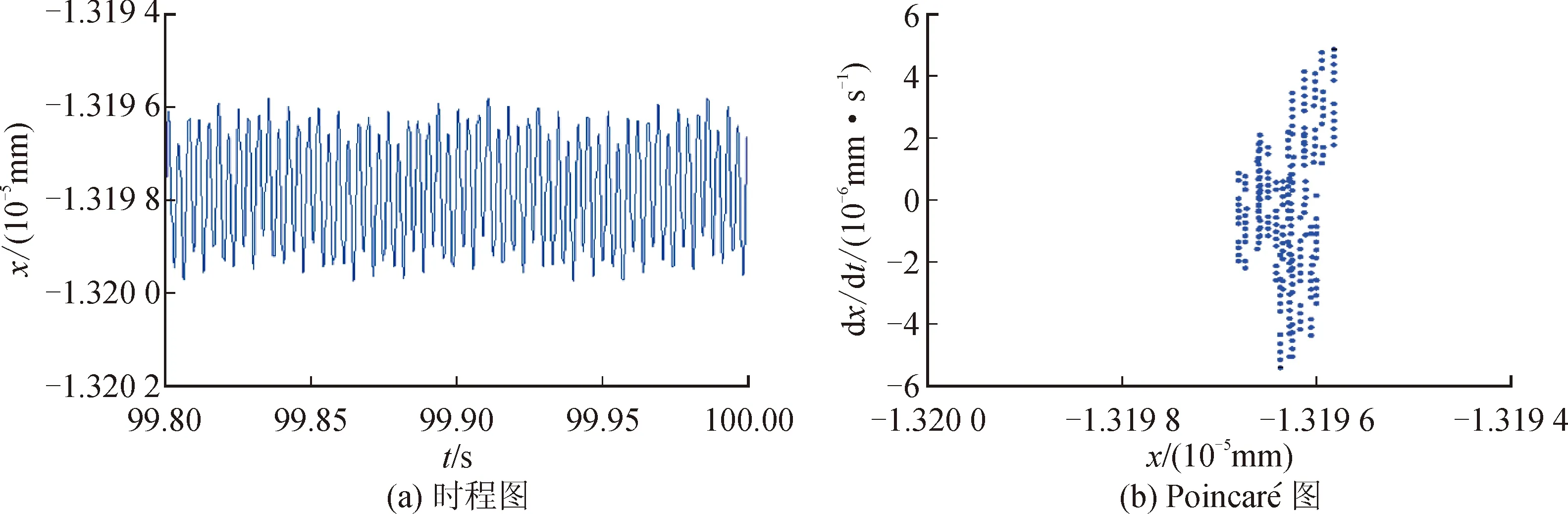
图5 转速ω=15 000 r/min时的系统响应
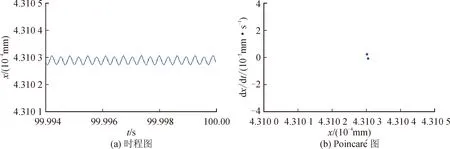
图6 转速ω=20 000 r/min时的系统响应
由图3~6可知,当转子转速为5 000 r/min时,系统时程图呈周期性变化,且Poincaré图上为11个孤立的点,则系统为周期11(P11)运动,此时系统最大振幅达到9×10-9mm。当转子转速升高为10 000 r/min时,时程图历程杂乱无章、无规律可循,且Poincaré图上出现了大量无序的点。因此,此时系统处于混沌(chaos)运动状态,且最大振幅达到8×10-6mm。同理,当转速为15 000 r/min时,系统仍处于混沌(chaos)状态,此时系统最大振幅达到1.32×10-5mm。当系统转速升高为20 000 r/min时,Poincaré图上出现了2个孤立的点,则系统处于周期2(P2)运动状态,且系统最大振幅为4.31×10-4mm。
由上可知,电主轴转子-轴承系统的主轴振幅随转速变化的变化趋势为: 9×10-9mm→8×10-6mm→1.32×10-5mm→4.31×10-4mm。可知,主轴振幅随转速的增加而增加。原因在于,转速的增加使得不平衡质量引起的离心力显著增强,导致系统振幅增加。当转速为5 000 r/min、20 000 r/min时,系统时程图表现为周期变化的趋势,且Poincaré图上存在若干孤立的点,则表明系统处于周期运动状态。转速为10 000 r/min、15 000 r/min时,Poincaré图出现大量无序的点,系统为混沌运动,随着转子转速的升高,系统运动特性为P11→chaos→P2。
2.2 不同转速下的响应(k1=2.248 8×1010 N/m)
轴承刚度为k1=2.248 8×1010N/m,以ω作为控制参数,系统时程图、Poincaré图分别见图7~10。
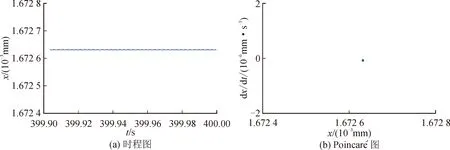
图7 转速ω=5 000 r/min时的系统响应
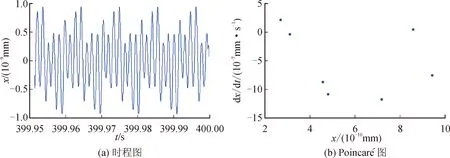
图8 转速ω=10 000 r/min时的系统响应
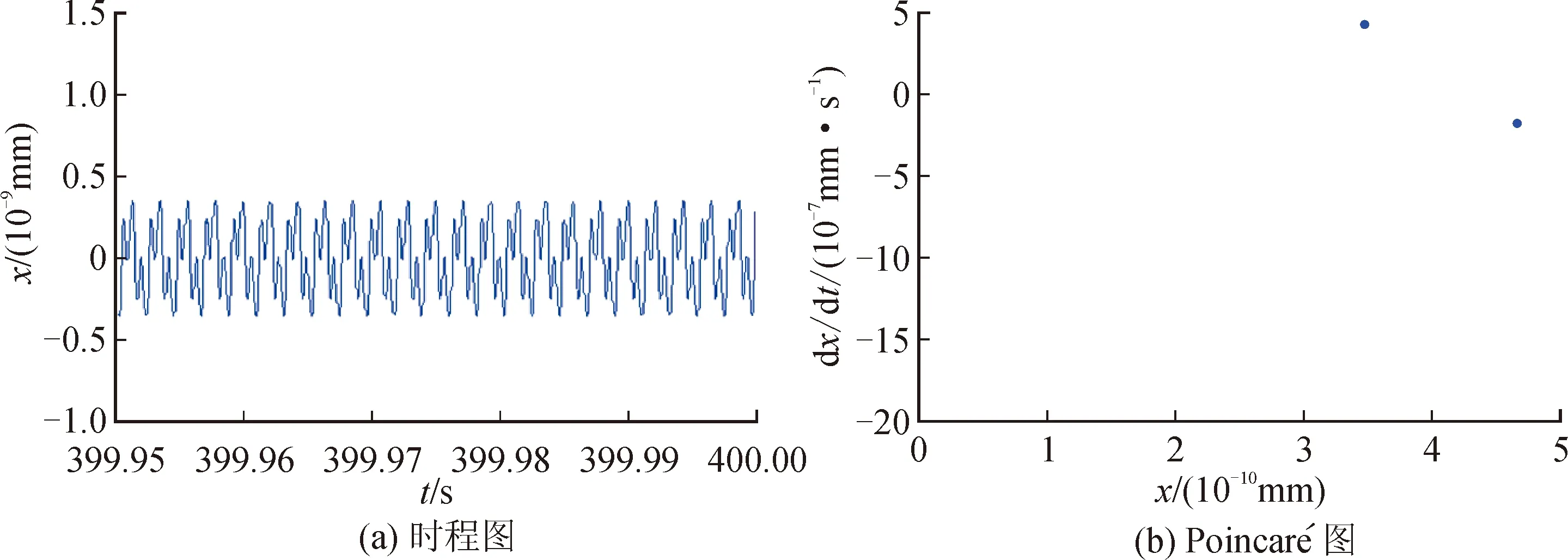
图9 转速ω=15 000 r/min时的系统响应
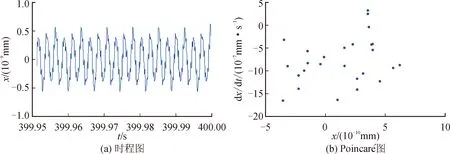
图10 转速ω=20 000 r/min时的系统响应
由图7~10可知,当转子转速为5 000 r/min时,系统时程图呈周期性变化,且Poincaré图上存在1个孤立的点,则系统运动为周期1(P1)运动,此时系统最大振幅达到1.672 6×10-3mm。当转子转速升高为10 000 r/min时,Poincaré图上出现可数个孤立的点,则此时系统为周期7(P7)运动,此时系统最大振幅达到1×10-9mm。同理,当转速为15 000 r/min时,系统为周期3(P3)运动,此时系统最大振幅达到4×10-10mm。当系统转速升高为20 000 r/min时,Poincaré图上出现可数个孤立的点,则系统处于周期n(P-n)运动状,此时系统最大振幅达到5×10-10mm。
分析图7~10可知,主轴振幅随转速的变化趋势为:1.672 6×10-3mm→1×10-9mm→4×10-10mm→5×10-10mm。同时可以看出,转子轴承系统始终处于周期运动状态,即P1→P7→P3→P-n。
电主轴转子-轴承系统的动力学特性见表1。

表1 不同刚度下电主轴的运动特性
由表1可知,当k1=2.248 8×109N/m时,系统的运动状态随转速的增加而变化,从周期运动到混沌运动,最后再回到周期运动。当k1=2.248 8×1010N/m时,系统处于周期运动状态。由此可见,刚度的增加抑制了混沌的发生,改善了电主轴轴承-转子系统的振动特性。
电主轴转子-轴承系统的振动幅值见表2。

表2 不同刚度下电主轴系统振幅(单位:mm)
从表2可以看出,随着轴承刚度的增加,系统振幅呈现明显的下降趋势。文献[6]给出了转速为3 000 r/min时,不同刚度作用下转子振动响应幅值变化曲线,随着轴承刚度的增加,转子的径向振动幅值逐渐降低。理论仿真结果与文献结果具有相同的趋势,验证了文中模型的正确性。
3 稳定性分析
基于微分方程稳定性理论,式(4)可用一阶常微分方程组表示:
(5)
在系统不受外力的情况下,则:
(6)
首先,得到系统式(6)的不动点:
(7)
因此,该系统有3个不动点:(0,0),(1,0)和(-1,0)。
将式子(7)写为矩阵形式:
(8)
a) 检查固定点(0,0)的稳定性:
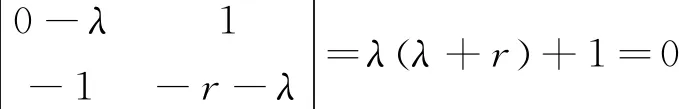
(9)
上式的解为:
(10)
1) 当r>0时,在固定点(0,0)处,λ1,2< 0,则该不动点是渐近稳定的;
2) 当r=0时,在固定点(0,0)处,λ1,2=± i,则该不动点是线性稳定的;
3) 当-2 4) 当r=-2时,在固定点(0,0)处,λ1,2=1,系统有两个正根,则该不动点是失稳的; 5) 当r<-2时,在固定点(0,0)处,λ1,2>0,则该不动点是失稳的。 b) 检查固定点(±1,0)的稳定性: (11) 上式的解为: (12) 由式(12)的第一个方程知,系统方程总是有一个正根,所以该不动点是不稳定的。 由式(4)可知,r=c/(m·ωn) > 0,所以在固定点(±1,0)附近,系统是失稳的,在固定点(0,0)附近,系统是渐近稳定的。 本文主要研究质量偏心及“负刚度”作用下,转速变化对电主轴转子-轴承系统动力学行为的影响。合理的转速能够避免系统进入混沌运行状态,为电主轴长期处于周期运行提供理论依据,指导实际加工中工艺参数的优化选择。 1) 系统支承刚度为k1=2.248 8×109N/m时,随着转速的增加,系统动力学特性经历了周期运动和混沌运动。当支承刚度增加到k1=2.248 8×1010N/m时,系统不出现混沌现象,呈现良好的系统稳定性。由此可知,系统刚度的增加抑制了混沌现象的发生,使得系统始终处于周期性运动状态。随着轴承刚度的增加,系统振幅呈现明显的下降趋势。 2) 系统稳定性分析表明,系统在不动点(±1,0)附近的运动是不稳定的;在不动点(0,0)附近的运动是渐近稳定的。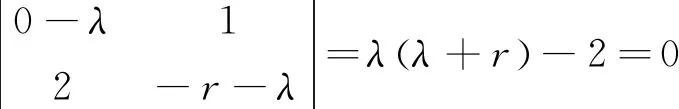
4 结 论
