时变时滞广域电力系统稳定性分析
2021-05-07
(湖南工业大学 电气与信息工程学院,湖南 株洲 412007)
1 研究背景
在自然界中,系统未来的发展趋势由当前状态和过去状态共同决定,这类系统称为时滞系统[1]。随着电力系统的发展和扩大,以及基于相量测量单元(phasor measurement unit,PMU)的广域量测技术(wide area measurement system,WAMS)的应用[2],导致信号传输的距离变远,然后产生延时,影响电力系统的稳定性。因此,研究时滞对电力系统稳定性的影响以及获取对应的时滞上界,有重要的现实意义。
目前,广大国内外学者对时滞系统稳定性判据推导的研究已经取得了许多成果。积分不等式被广泛地应用于时滞系统稳定性判据的推导中,主要有Jensen不等式、Wirtinger 不等式等。文献[3]指出,获取更大的时滞上界主要采取两种方法:其一为构建合适的L-K(Lyapunov-Krasovskii)泛函,其二为运用保守性更低的方法来处理泛函求导后产生的积分项。文献[4]在Wirtinger 不等式的基础上,提出了一种新的积分不等式,它比以往的更为严密,求得的时滞上界更大,并且可以用来对含有离散分布时滞的线性系统稳定性进行研究。文献[5]选用单机无穷大系统为算例系统,分析出励磁放大系数中的扰动项与系统时滞上界之间的变化关系,并且通过引用自由权矩阵积分不等式的方法来得到更大的时滞上界。文献[6]讨论了含扰动的时滞电力系统稳定裕度求解方法,提出了双层优化的追踪算法,可用于求解含扰动的时滞电力系统的时滞上界。文献[7]提出了一种新的改进型积分不等式,其中包含了Jensen 不等式,稳定性判据结论得到了很大的提高。文献[8]在考虑广域电力系统多条回路存在时滞的情况下,建立了含有多个时滞的系统模型,在构建L-K 泛函时舍掉了一些冗余项,然后加入二重积分项使系统保守性大大降低。文献[9]设计了一个含区间变时滞的广域电力系统控制器,采用扩展型积分不等式和凸组合等方法来降低稳定性判据的保守性。文献[10]根据广域电力系统测量的一些特点,考虑到本地信号传输时没有时滞,而区域间的信号传输有多个时滞,建立了含有多个时滞的电力系统模型,并根据Lyapunov 理论和线性矩阵不等式(linear matrix inequality,LMI)理论求出系统能承受的时滞上界。文献[11]先取得二次型积分项的极大值,再采用“时滞分割”的思想来获取稳定性判据,其计算效率更高,获得的结果也更好。文献[12]通过Pade 近似方法,可以将时滞部分转换成状态空间形式,然后建立含时滞的电力系统线性化模型,设计了一个阻尼控制器,能有效地减小系统时滞对阻尼控制效果的影响。文献[13]对时变时滞系统的稳定性问题进行了研究,通过提出一个基于广义自由权矩阵的积分不等式,得到了较大的时滞上界。文献[14]提出了一种基于改进自由权矩阵的时滞上界求取方法,在求解导函数时加入了一些必要的松散项,使得系统保守性降低。文献[15-16]研究了时变时滞电力系统的稳定性,但在处理泛函导数产生的积分项时,采用的方法过于保守,导致所求的时滞上界较低。
本文通过引入一个关于时变时滞的二次函数,以典型的二阶系统和四机十一节点系统为算例,再构建出新的Lyapunov 泛函,引用文献[4]和文献[7]的积分不等式和二次型稳定性判定方法,使得时滞电力系统稳定性判据的保守性明显降低。最后,通过仿真实例,说明采用本文方法得到的稳定裕度具有更低的保守性,证明所提方法的可行性和优越性。
标号注释:Rn×m表示n×m阶矩阵空间;上标-1为矩阵的逆,T 为矩阵转置;R>0 表示矩阵R对称且正定;I表示合适维度的单位矩阵,0 表示零矩阵;sym{X}=X+XT。
2 系统建模
一般情况下,时变时滞电力系统模型可用如下微分方程组表示:
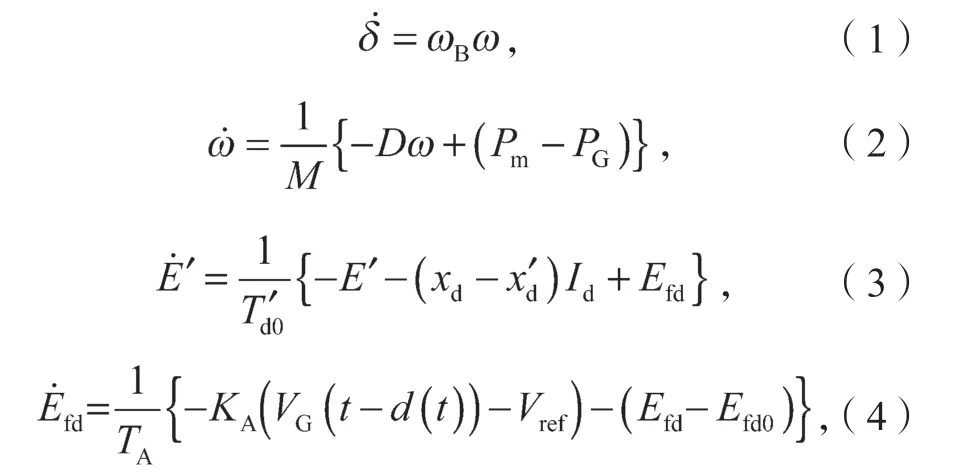
式(1)~(4)中:ω为发电机功角;
ωB为发电机角速度;
M为惯性时间常数;
D为阻尼系数;
Pm为原动机输出电磁功率;
T′d0为发电机定子开路时间常数;
E′为电抗后电势;
xd为发电机稳态电抗;
x′d为发电机暂态电抗;
KA为励磁回路放大系数;
TA为自动调节器的时间常数;
Efd为线路励磁电势;
Efd0为励磁电势的参考值;
Vref为机端电压参考值;
Id为纵轴输出电流,且
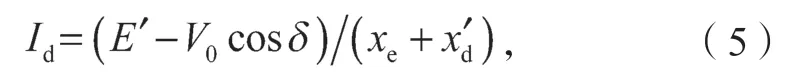
其中,V0为无穷大母线端电压,xe为线路电抗,δ为系统额定角速度;
PG为发电机输出功率,且
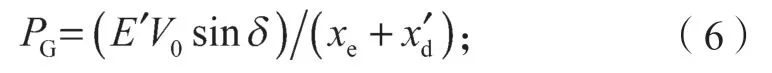
VG为发电机机端电压,且
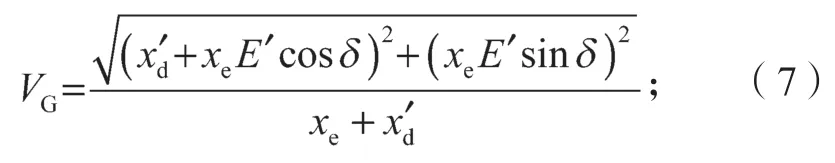
将式(1)~(4)进行线性化处理,可以得到如下含时变时滞的系统模型:
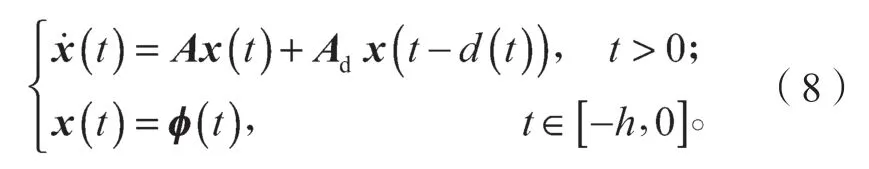
d(t)是一个连续函数,且满足
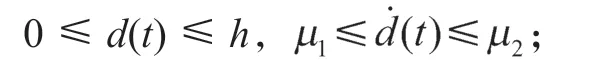
A、Ad为系统矩阵。
引理1定义x在区间[α,β]→Rn上是可导函数,当对称矩阵,N1,N2,N3∈R4n×n时,则有以下不等式成立[4]:
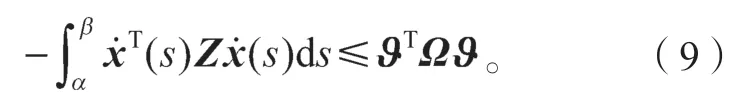
其中,τ=β-α;
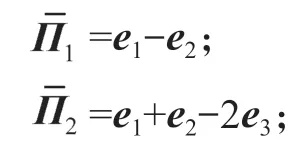
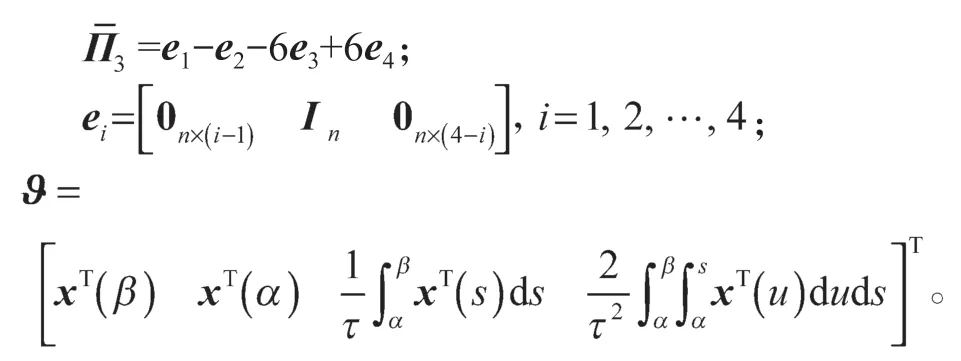
引理2考虑二次函数f(x)=a2x2+a1x+a0,其中x∈[h1,h2],a2,a1,a0∈R。对于给定一个非负整数N,假设i=1,2,…,2N,满足以下条件[17]:
Ⅰ)f(h1)<0,
Ⅱ)f(h2)<0,
则f(x)<0。
注释文献[7]给出的条件仅使用一条切线约束二次函数,引理2 与文献[7]的方法相比较,使用了2N+1 条切线约束二次函数,随着N的增加,引理2给出的条件保守性越低。
3 主要结论
本节先给出以下向量和矩阵的定义:
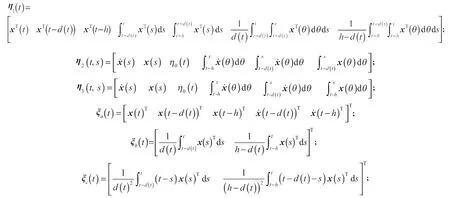
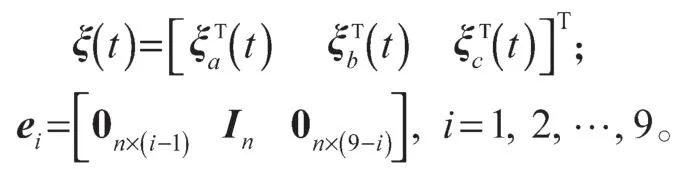
下面给出本文定理:
定理1给定标量μ1<μ2<1,h>0,如果存在矩阵任意矩阵N1、N2、N3、M1、M2、M3∈R9n×n,对于满足约束条件0≤d(t)≤h、μ1≤≤μ2时,使得LMIs(10)~LMIs(12)有可行解,则系统(8)是渐近稳定的。

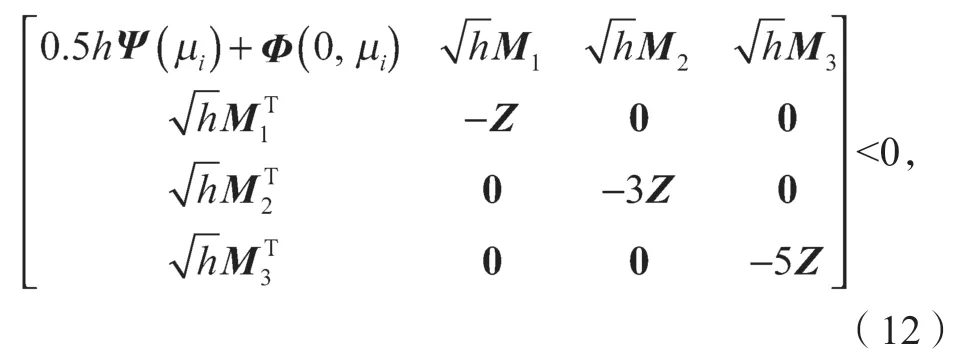
这里i=1,2,且式(10)~(12)中:
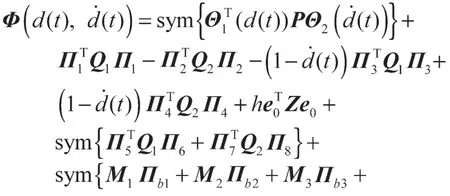
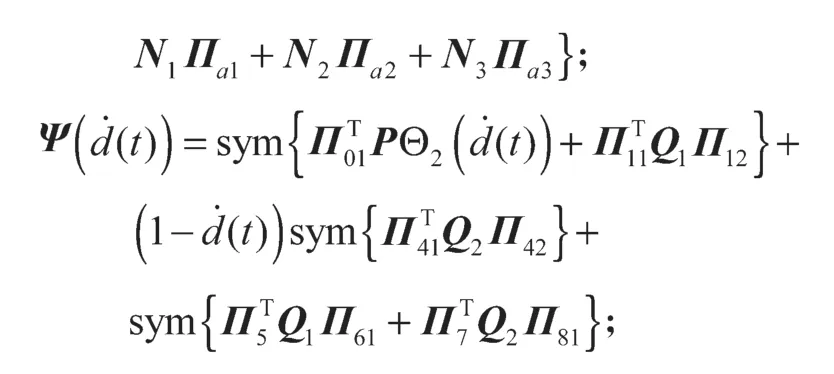
其中:
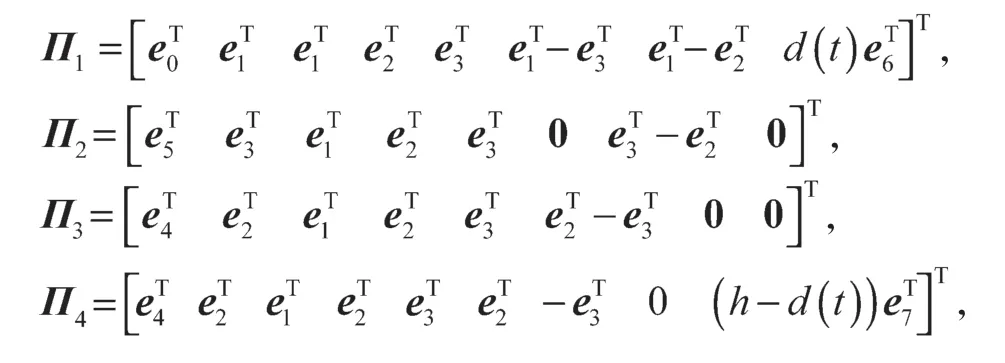
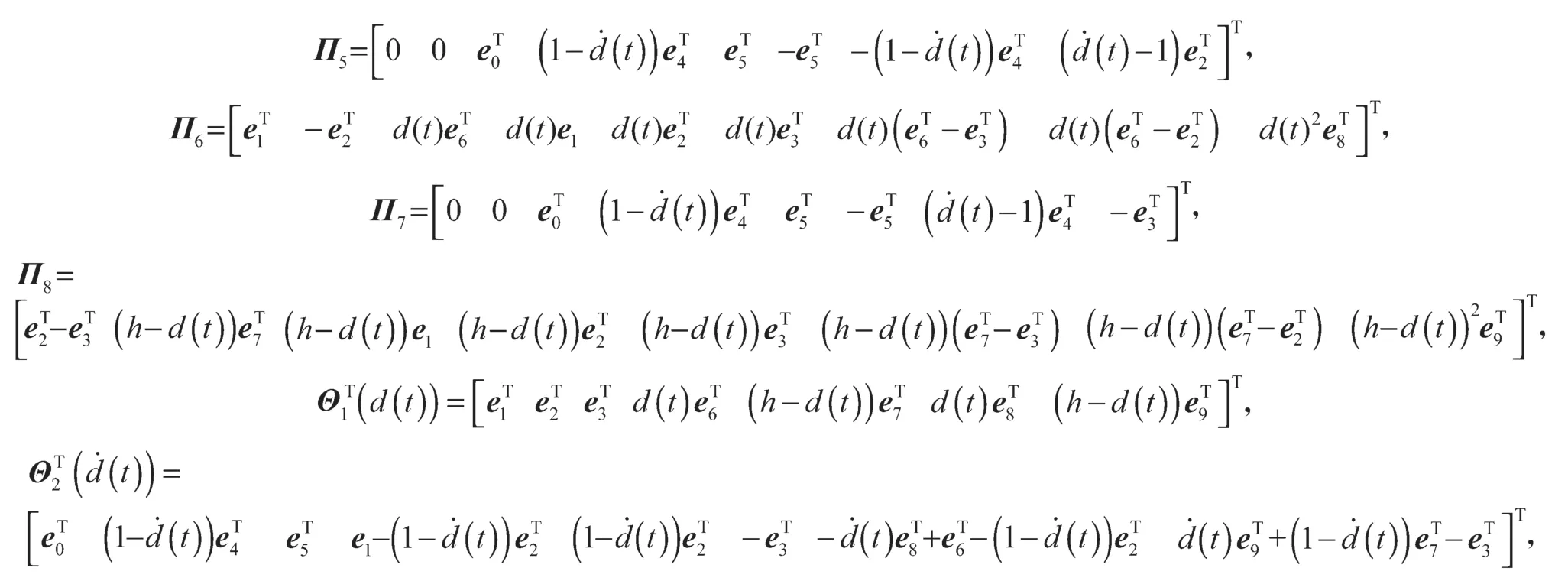
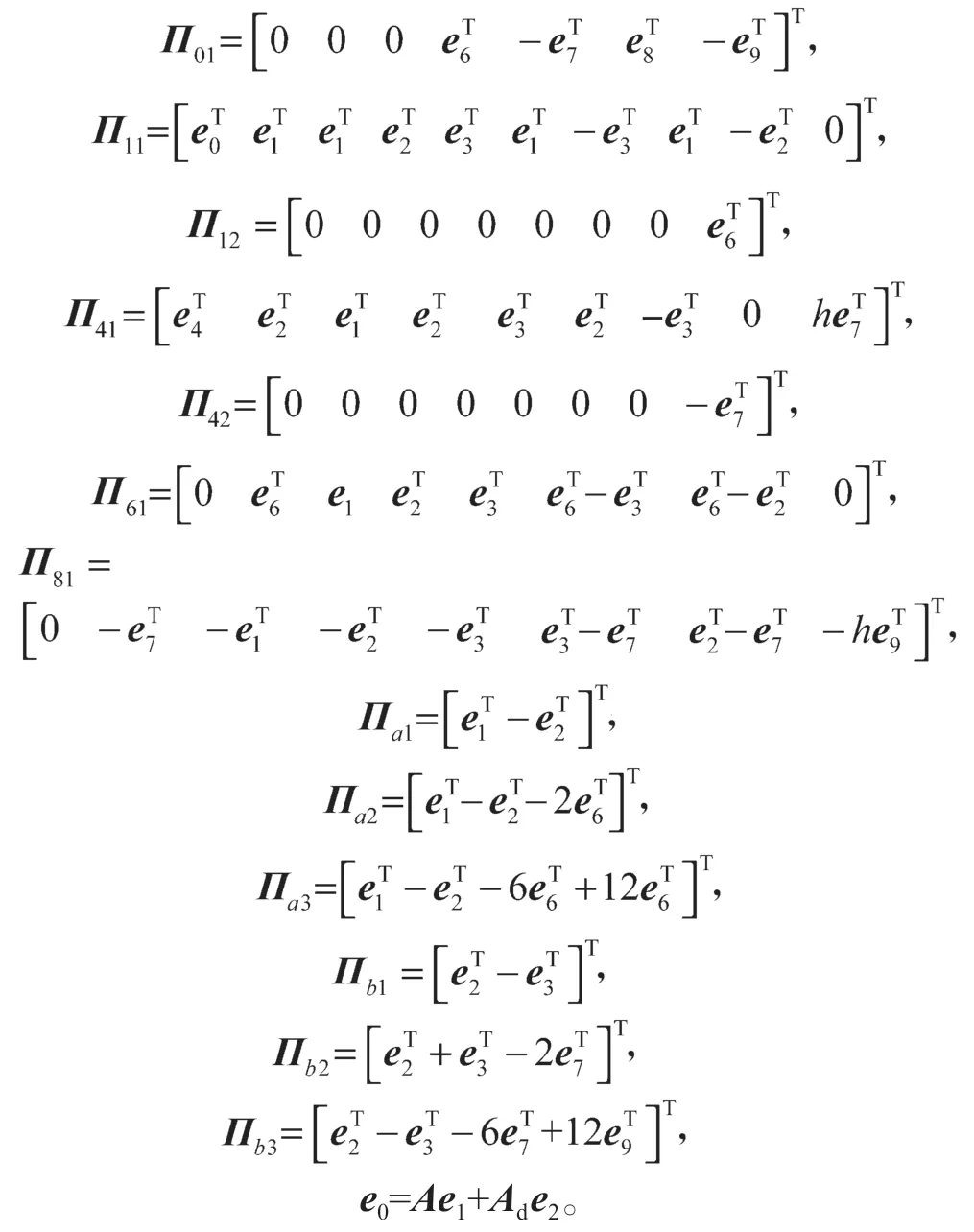
证明构建如下Lyapunov-Krasovskii 泛函:
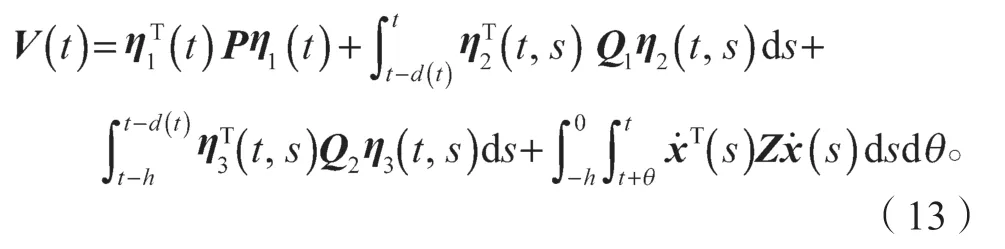
对式(13)求导,可得:
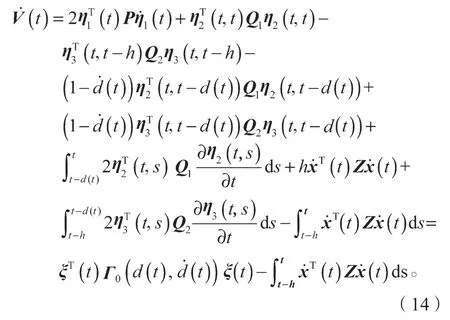
式(14)中:
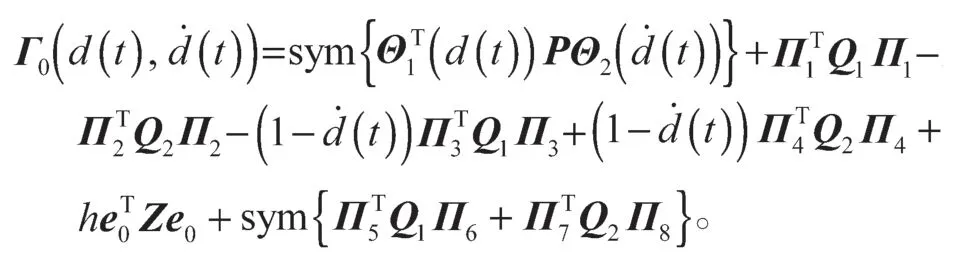
然后把式(14)中[t-h,t]分为[t-h,t-d(t)]和[t-d(t),t]两个区间,再对两个区间分别运用引理1 可得:
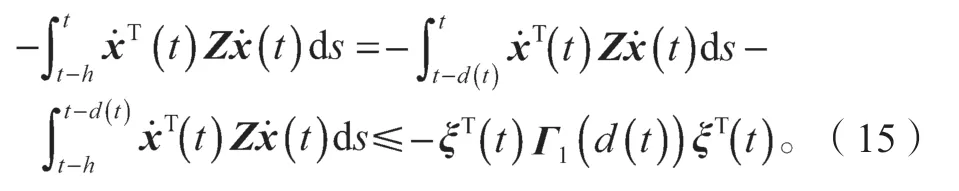
式(15)中:
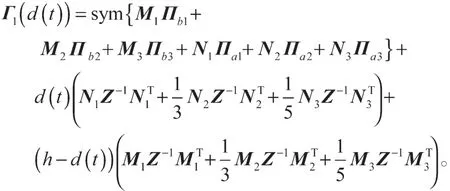
结合式(14)和(15)可得:
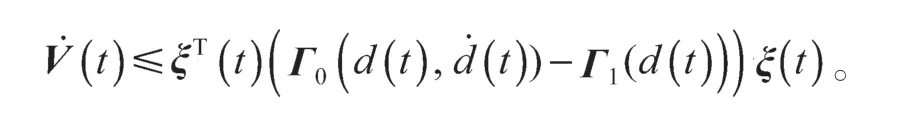
应用引理2,当N=0 时,结合Schur 补定理,得到式(10)~(12)。如果存在矩阵,,,,任意矩阵N1、N2、N3、M1、M2、M3∈R9n×n,当满足约束条件0≤d(t)≤h,μ1≤≤μ2,且式(10)~(12)成立时,则。再根据李雅普诺夫稳定性理论,得到系统(8)为渐近稳定的,证毕。
4 算例分析
4.1 典型二阶系统
本节采用典型的二阶时滞系统进行仿真分析,并将仿真结果与文献[7]、[13]和[15]中的结果进行比较,取μ=μ2=-μ1时,得到在不同μ值下时滞上界的大小,如表1所示。
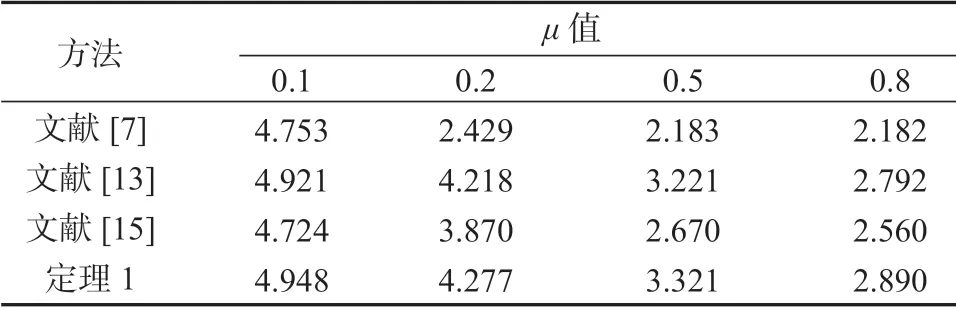
表1 不同μ 值时求得的时滞上界Table 1 Upper bound of time delay for different valuess
分析表1中的数据可知,根据定理1 得到的不同μ值下的时滞上界比相关文献得出的数据大,即定理1 可以得到更大的时滞上界,说明相比已有研究,本文给出的方法获得的结果具有一定的优越性。
4.2 四机十一节点系统
本节采用四机十一节点系统进行仿真分析,并将仿真结果与文献[14]~[16]的结果进行比较,系统模型如图1所示。
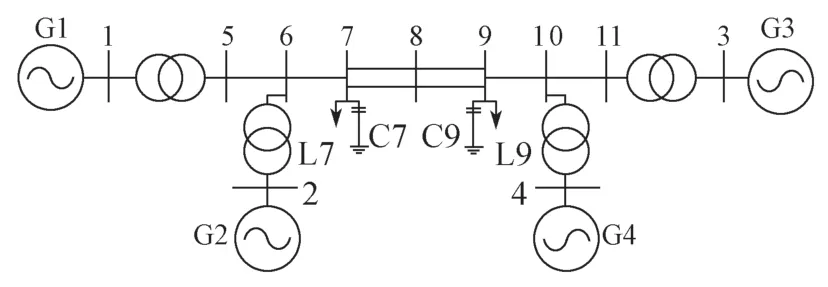
图1 四机十一节点系统示意图Fig.1 Four-generator eleven-bus power system
接下来采用文献[15]中降维后的状态矩阵A、时滞矩阵Ad进行仿真分析获得结果,A、Ad描述如下:
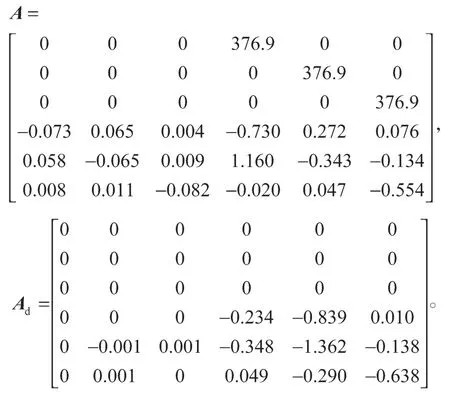
根据定理1,当μ=0 时,得到如表2所示结果,从表中数据可以得知,本文方法所得时滞上界相比其他文献的时滞上界更大、保守性更小,进一步说明了本文方法的可行性和优越性。

表2 不同方法获得的四机十一节点系统的时滞上界Table 2 Upper bound of time delay obtained by this method with other literature methods
5 结语
本研究以典型的二阶系统和四机十一节点系统为算例,研究了含时变时滞的电力系统稳定性判据。首先,建立含有时变时滞的广域电力系统模型,构建出新型L-K 泛函;然后,通过引入一个关于时变时滞的二次函数和积分不等式,得到一种保守性更小的稳定性判据;最后,通过仿真分析,并与已有文献方法比较,得知本文给出的方法能够获得更大的时滞上界,说明了本文方法的可行性和优越性。
