Investigation of cavitation bubble collapse in hydrophobic concave using the pseudopotential multi-relaxation-time lattice Boltzmann method∗

Minglei Shan(单鸣雷), Yu Yang(杨雨), Xuemeng Zhao(赵雪梦),Qingbang Han(韩庆邦), and Cheng Yao(姚澄)

1Jiangsu Key Laboratory of Power Transmission and Distribution Equipment Technology,Hohai University,Changzhou 213022,China

2College of Computer and Information,Hohai University,Nanjing 210000,China

Keywords: cavitation bubble,hydrophobic concave,lattice Boltzmann model,pseudopotential model

1. Introduction

Cavitation is an important phenomenon accompanied by extreme physical situations, which means high velocity, high pressure, and high temperature occurring in local domain.When cavitation happens in the vicinity of solid surfaces, it can cause damage to materials,which is called cavitation erosion.However,there are some applications utilizing cavitation properties,such as material surface modifications and medical fields. Thus,some general issues can be extracted from these applications, i.e., the study of the interaction between cavitation and solid surface with different properties.

The interaction between cavitation and solid surface has been discussed in many researches from different aspects,including the geometry of the surface, interfacial wettability,and the roughness of the surface. Li et al. studied the effect of nozzle inner surface roughness on the cavitation erosion characteristics of high-speed submerged jets through physical experiments.[1]Their finding showed that geometric characteristic of the surface has great effects on cavitation erosion intensity at standoff distances around or exceeding the optimum.Li et al.[2]investigated the effect of Venturi tube geometry on the hydrodynamic cavitation for the generation of microbubbles. They found that the cavitation inception is determined by flow resistance, which significantly depends on the geometrical design of the Venturi tube. Additionally, Belova et al.studied the controlled effect of ultrasonic cavitation on hydrophobic/hydrophilic surfaces.[3]They developed a selective control scheme of ultrasonic cavitation to explore the effect of wettability on cavitation. Their finding showed that the cavitation prefers to dominate on the hydrophobic surfaces due to the low nucleation barrier.The above experiments investigated the interaction between cavitation and solid surface at the macro level. However,the microcosmic mechanism of them has not been discussed in their work due to the limitations of the experiment.

The lattice Boltzmann method (LBM) has been rapidly developed in recent years due to its convenience for multiphase and fluid–solid surface modeling.[4–7]The LBM has high potentials to simulate complex physical phenomena such as the multiphase flows in complex geometries. Moreover,the LBM fully considers the liquid–liquid and liquid–surface interactions during the phase change processes. Therefore, the LBM is favored by scholars who study the multiphase flow including heat transfer,droplet dynamics,and cavitation.[8–11]By virtue of the LBM’s high efficiency and simplicity in describing wettability,Ezzatneshan discussed the effect of wettability on cavitation.[12]It shows that the pseudopotential LBM is efficient to simulate the cavitation inception. However,their works did not involve the effect of geometry and wettability on cavitation,which is critical for the interaction between the cavitation and solid surface.

The difficulty of simulation of the cavitation in the vicinity of the solid surface is the stability of the lattice Boltzmann (LB) model. The stability of the model can be simplified to keep the thermodynamic consistency. Many works have been made for this issue. Recently, Shan et al.[13–16]studied the effect of the wettability on collapsing cavitation bubble near solid surface by multi-relaxation-time(MRT)lattice Boltzmann model. They added the improved Li’s forcing scheme[17,18]for the thermodynamic consistency and the fluid–solid interaction into the simulation model for wettability interfaces to establish the collapsing bubble model. It demonstrated that the pseudopotential MRT-LB can successfully simulate the collapsing cavitation bubble near the solid surface with different wettabilities.But the combined effect of solid surface wettability and geometry on cavitation is still an open topic.

In order to study the combined effect of solid surface wettability and geometry on cavitation, we set up an MRT-LB model to investigate the hydrodynamics of a single cavitating bubble near rough surface. In our scheme, the rough surface is simplified as concave corner to characterize the pits of rough surface. Moreover, the improved pseudopotential multiphase model,which is modified by Li’s forcing scheme[13,14]is adopted to simulate the whole flow field.The adhesive force of solid surface is considered to tune the wettability of surface.

The rest of this paper is arranged as follows. Section 2 shows the fundamental theory about the pseudopotential MRTLB. Section 3 explores the effect of concave corner and the wettability on the cavitation. Section 4 is the conclusion and mechanism analysis.

2. Pseudopotential MRT-LB model

The pseudopotential LB model with MRT operation collision was employed in the present work.[19–21]The evolution equation can be given as

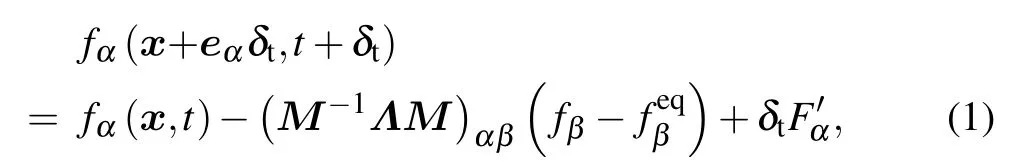
In the pseudopotential LB model, the intermolecular interaction force is defined via a pseudopotential ψ, which depends on the local density. It is given as[22]

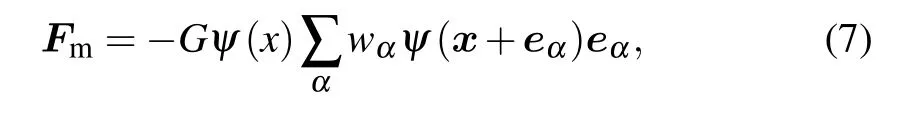
According to Yuan and Schaefer,[27]the pseudopotential ψ is taken as

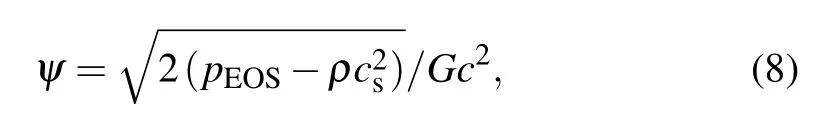
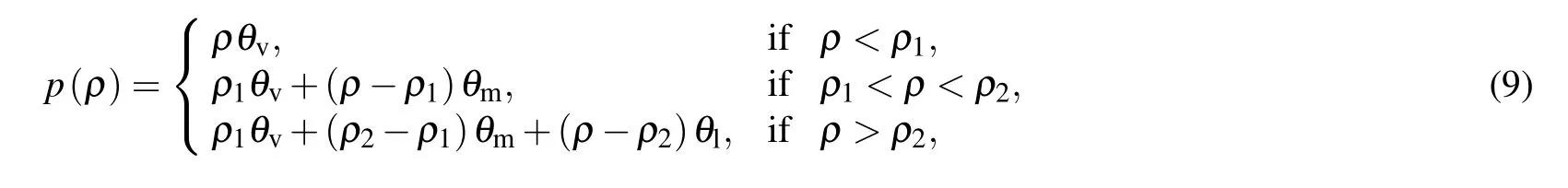
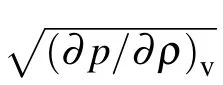
and the other is ensured for chemical equilibrium

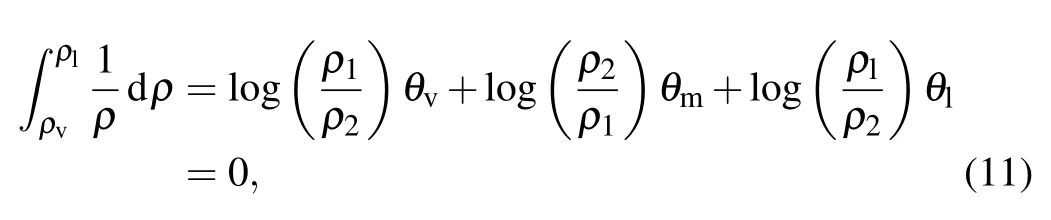
where ρland ρvrepresent the density of liquid and vapor,respectively.

With the pseudopotential ψ, the pseudopotential LB model usually undergoes thermodynamic inconsistency. Subsequently, Li et al.[14]found that the thermodynamic consistency can be approximately achieved by adjusting the mechanical stability condition via an improved forcing scheme[13]

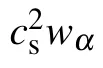
In this paper,the lattice units for LB are adopted. The basic units of length,time,and mass are lu(lattice unit),ts(time step),and mu(mass unit),respectively. Thus,the units of velocity,pressure,and density are expressed as lu/ts,mu/(ts2·lu),and mu/lu2,respectively.

3. Simulation and analysis

3.1. Laplace law and the contact angle

Laplace law is the validation of the multiphase model.For the case of the cavitation bubble,the Laplace law can be given as

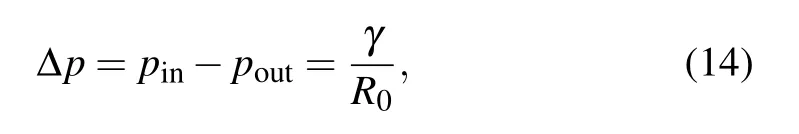
where the pinand poutare the pressures inside and outside of the bubble,respectively. R0is the radius of the bubble,γ is the surface tension. In a 700×700 lattice computational domain,the periodic boundary condition is applied in two directions of the boundary. A vapor bubble is initialized at the center of the computational domain(x0,y0)as[7]

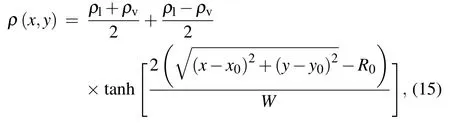
where W is the prescribed width of the phase interface and it is 5 in the present work. The‘tanh’is a hyperbolic tangent function. The density ratio is set as 500 in all cases in the present work with ρl=500 and ρv=1. Additionally, other parameters in the present work including ρ1,ρ2,θv,θm,and θlare set as 1.36,481.04,0.2133,−0.01333,and 0.33333,respectively.The lattice constant c and the time step δtare both set as 1.

Figure 2 shows the linear relationship between the ∆p and 1/R0. It indicates that the simulation results agree well with Laplace law and verify the pseudopotential MRT-LB model adopted.

In this paper, the wettability of the surface is measured by the achievable contact angle. It is a general practice that the wettability is obtained by measuring the contact angle of a droplet on the solid surface. The contact angle θ >90◦means the surface is hydrophobic and θ < 90◦means the surface is hydrophilic. For the contact angle measurement, a 400×400 lattice system computational domain is adopted, and the open boundary condition is employed at the top boundary.[30]In our model, open boundary is applied to the flat single solid wall cavitation bubble collapse model,and its main function is to construct semi-infinite physical boundary in the single solid wall cavitation bubble collapse model. The nonslip boundary scheme[31,32]is applied at the bottom boundary as f5= f7−0.5(f1−f3)−0.25δt(Fx+Fy),f6= f8+0.5(f1−f3)+0.25δt(Fx+Fy), and f2= f4. The density field was initialized as[14]

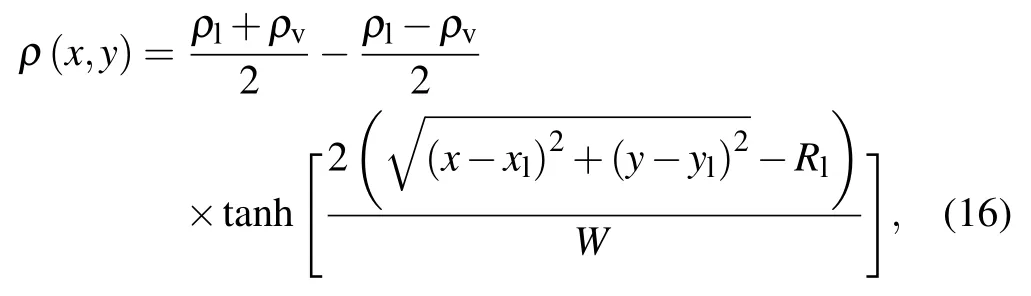
where (xl,yl) is the center of the droplet. The parameter Rlwhich represents the radius of the droplet is initialized as 40.

In the simulations, the intermolecular interaction force and the fluid–solid interaction force are used at the solid surface. Consequently, a contact angle of θ =90◦can be analytically achieved when Gwis 0 which represents the neutral wettability. The results of contact angles corresponding to different Gware shown in Fig.3. The obtained contact angle θ is 91.5◦when Gwis set as 0. This means that the numerical result is in good agreement with the analytical solution. As is shown in the results, the contact angle is approximately proportional to the parameter Gw. In other word, the wettability of the solid surface can be adjusted by Gwin the simulation.

安顺煤矿所出产的原煤在地面筛分厂经过三台振动筛四层筛面筛选为5个粒度等级，依次为粉煤(1cm以下)、粒煤(1-3cm)、小块煤(2-5cm)、中块(5-8cm)、大块煤(8cm以上)。

3.2. Verification of the collapsing bubble in concave corner

Using the above improved pseudopotential MRT-LB model and the fluid–solid force scheme, the collapsing cavitation bubble in concave corner model is constructed in this section. The computational domain for the collapsing bubble is established in 700×700 lattice system. As shown in Fig.4,the nonslip boundary scheme is adopted to describe the orthogonal solid wall which constructs a concave corner.R is the initial radius of cavitation bubble and is set as 70 in the follow cases. p∞and pvrepresent the external pressure and internal pressure of cavitation bubble, respectively. b1and b2represent the distance from the center of cavitation bubble to the solid wall,respectively,and b1=b2=80 in the follow cases.λ =b1/R is defined as the nondimensional position offset parameter and λ =1.14 in this case. The constant pressure difference ∆p=p∞−pvis 18.334 to ensure the cavitation bubble collapse. The parameter Gwin fluid–solid interaction is 0.

For the nonslip boundary,the unknown distribution function components of the bottom can be obtained as

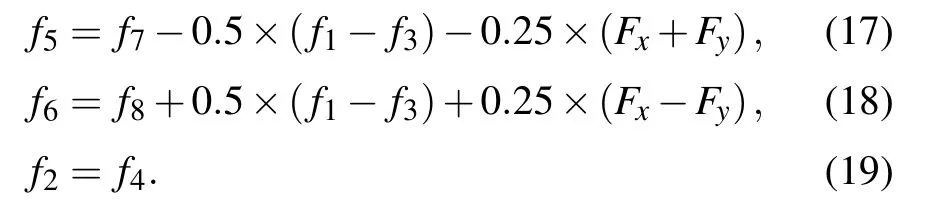
For the left wall

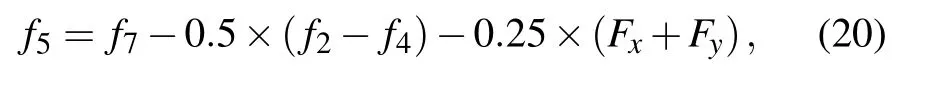
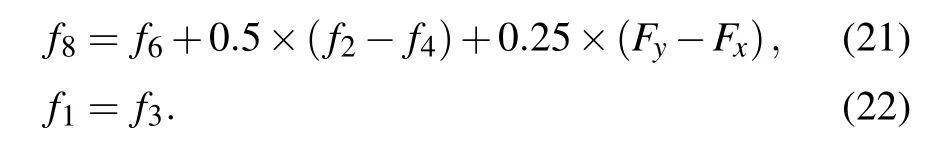
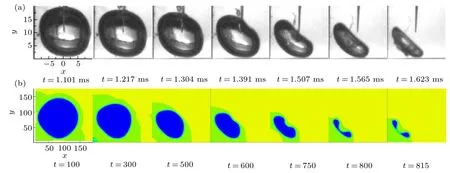
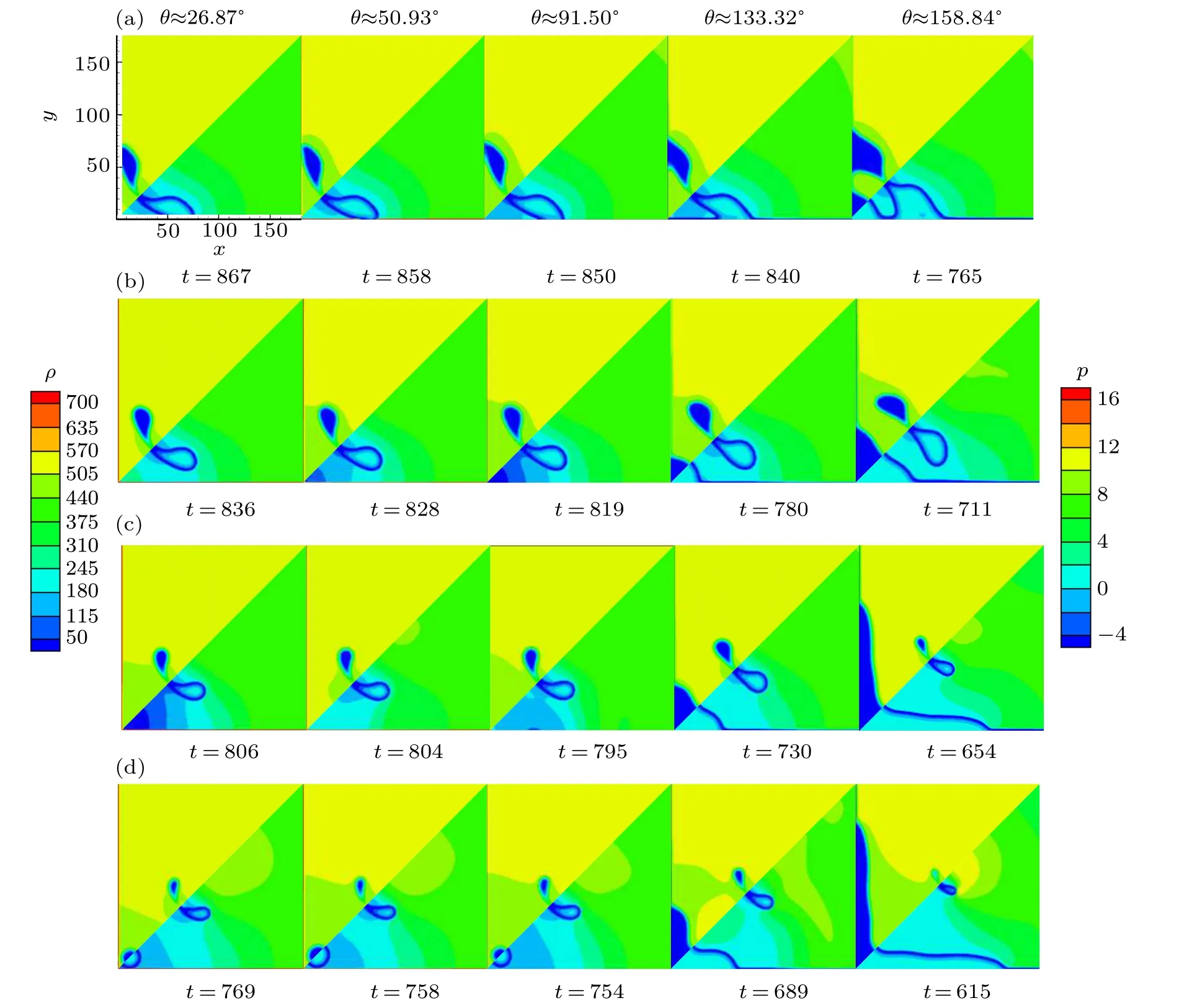
The numerical results of the evolution for cavitating bubble in concave corner are compared with the experiment ones in Fig.5.In the cavitation bubble collapse,the shape of cavitation bubble is symmetric about the diagonal. First,the spherical cavitation bubble begins to collapse in the initial state,followed by the formation of collapse depression in the diagonal direction of the spherical cavitation bubble. Then the extent of the depression becomes larger, gradually forms an oblique bowl of the depression.Finally,the cavitation bubble collapses like a bowl(a ring in three dimensions)above the diagonal direction. The comparison between the physical experimental results of group (a) and the numerical simulation results of group (b) indicates that the numerical simulation results are with the experimental results.

In addition, the bubble evolution from the initial state to collapse at different grid resolutions can be observed in Fig.6.The criterion for the interface between the bubble and liquid is that the density of the point is equal to(ρv+ρl)/2.We adopted 300×300, 500×500, and 700×700 lattice regions, respectively. According to the same proportion principle,the initial bubble radius is R0=30,50,and 70. Moreover,a dimensionless time T∗is defined, which represents the time from the initial state to the first collapse. We extracted bubble profiles at 0, 0.2T∗, 0.4T∗, 0.6T∗, 0.8T∗, and T∗under various grid resolutions, and normalized the acquired coordinate points in the x and y directions.

The normalized profiles of the cavitation bubble collapse in concave corner almost coincide with one another under different grid resolutions. In order to focus on physical evolution processes in a more detail,the simulation was carried out in the 700×700 lattice region in the manuscript. The effectiveness of the collapsing cavitation bubble in concave corner model is verified.

3.3. Density,pressure,and velocity fields result and mechanism analysis

The effect of wettability on the collapsing cavitation bubble in concave corner may be further analyzed from the density,pressure and velocity of collapsing bubble. In the following,we investigate the effect of solid surface wettability on the collapsing cavitation bubble in terms of density,pressure,and velocity.

As shown in Fig.7,the number of rows in the figure represents different contact angles. Each row shows the process of collapsing cavitation bubble with the same wettability. The number of columns represents the time step which is 200,400,600, and 700. Each column shows the process of collapsing cavitation bubble with different wettabilities.

Figure 7 shows that cavitation bubble always collapses diagonally from the sphere.First,the bubble gradually collapses from the diagonal direction above the cavitation bubble, then the cavitation bubble is compressed into a bowl placed diagonally,and finally the cavitation bubble collapses.

The evolution of cavitation bubble does not change much when the orthogonal solid surface is hydrophilic. When the contact angle of the solid surface θ≈133.32◦, new bubbles gradually appear in the lower left corner, and their shape is merged from two micro-arch bridge bubble into a quarter circle bubble. With the collapse of bubble, the newly formed bubble gradually becomes larger. When the solid surface contact angle θ ≈158.84◦,the new bubble in the lower left corner of the solid surface becomes more obvious. Meanwhile, the new bubble gradually squeezes the collapsing cavitation bubble,making the former cavitation bubble collapse into barbelllike bubble. At the same time step,the area of collapse bubble under the condition of hydrophobic is smaller than that under the condition of hydrophilic. In addition,the cavitation bubble under the condition of hydrophobic collapses faster than that under the condition of hydrophilic,and the bubble is squeezed harder. It is demonstrated that the hydrophobic concave surface can accelerate the cavitation bubble collapse, while the hydrophilicity has little effect. Moreover, the hydrophobic concave surface tends to generate new cavitation bubble from the concave. The expanding new cavitation bubble squeezes the collapsing cavitation bubble and accelerates its collapse.The above results indicate that the surface wettability significantly affects the characteristics of cavitation bubble collapsing.

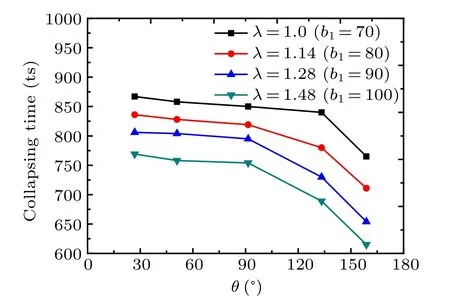
In order to study the effect of wettability on collapse time,the collapse time diagram of cavitation bubble with different wettabilities of concave corner is shown in Fig.8. It shows that with the strengthening of hydrophobicity, the collapsing time decreases sharply. As the cavitation bubble moves away from the solid surface,its collapsing time becomes shorter and the collapse speed becomes faster. In conclusion, as the hydrophobicity of solid surface increases,the collapsing time of cavitation bubble becomes shorter and the evolution of cavitation bubble is accelerated. Meanwhile,the farther away from the solid surface,the faster the collapse speed is.

3.3.2. Pressure field of the first collapse

Wettability affects not only the evolution of density field,but also the evolution of pressure field during the cavitation bubble collapse. Figure 9 shows the comparison of density and pressure fields at time of the first collapse of cavitation bubble in concave corner. The density field is at the top left and the pressure field is at the bottom right.In Fig.8,each row represents collapsing cavitation bubble diagram with different position parameters. Each column represents the collapsing cavitation bubble with different contact angles.

As can be seen from Fig.9, when the concave surface is hydrophilic, the pressure field and density field of collapsing cavitation bubble change little with different λ. When the solid surface is hydrophobic,the high-pressure area in the upper right becomes more concentrated and the pressure becomes larger. The pressure of the low-pressure area decreases,and the low-pressure area becomes more dispersed. This phenomenon becomes more pronounced as the cavitation bubble moves away from concave corner. Moreover,in this case,the new cavitation bubble in concave corner squeezes the original cavitation bubble and accelerates the cavitation bubble collapse.

3.4. Jet velocity evolution

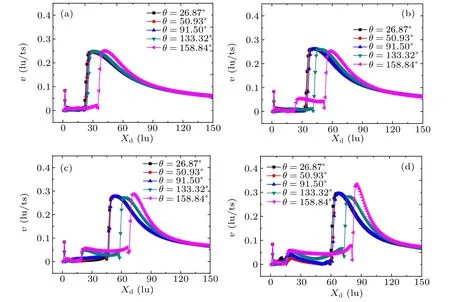
Wettability affects the jet velocity of collapsing cavitation bubble in concave corner.To explain the impact on jet velocity better, the jet velocity of perpendicular bisector of collapsing cavitation bubble on the diagonal symmetric line is discussed separately. In Fig.10,panels(a),(b),(c),and(d)show the jet velocity diagrams with different λ. The x axis represents the axisymmetric length of the bevel angle, which is represented by Xd. The y axis is the jet velocity of perpendicular bisector of x axis in the y direction.

As can be seen from Fig.10, the change trend of the jet velocity of perpendicular bisector of x axis in the y direction is first from around 0.1 to around 0. As the number of Xdincreases, the speed suddenly increases to an extreme value.Then the jet velocity of the perpendicular bisector of x axis in the y direction decreases slowly and becomes stable. When the solid surface is hydrophilic, its velocity change curve is not large. When the solid surface is hydrophobic,the velocity rises to the extreme value when Xdis larger, and the extreme value of the velocity increases. This phenomenon becomes more obvious as the cavitation bubble is away from the concave corner.

3.5. Mechanism analysis of wettability and geometric effects

When the surface is hydrophobic,the hydrophobicity increases the repulsive force between solid wall and fluid, and decreases the density(as shown in Fig.7)and the pressure(as shown in Fig.9) at the interface. As a result, the cavitation threshold is decreased,so cavitation nuclei are formed and developed more easily at hydrophobic surface. Further,because of geometric effect of concave corner,the cavitation regeneration is easier to occur in the hydrophobic concave corner than near the plane solid wall[11](as shown in Figs.7 and 9). The growth of the regenerated bubble further squeezes the original cavitation bubble and accelerates the evolution of cavitation bubble collapse. So, the collapse time is decreased with the same λ as concave surface is hydrophobic(as shown in Figs.8 and 9). Additionally,the regenerated bubble pushes the original cavitation bubble away from the concave corner and makes λ larger.

As we know, the role of solid wall on cavitation bubble collapse is the retarding effect on fluid. Due to the nonslip effect, the closer the cavitation bubble is to the solid wall, the more obvious the retarding effect is. Because of geometric effect of concave corner, this retarding effect is exacerbated.So, the cavitation bubble collapse is significantly lengthened when λ is smaller in concave corner (as shown in Figs. 7, 8,and 9). In addition,with the surface hydrophobicity,the concave corner gets stronger capillary effect which can push the cavitation bubble away from the corner and makes λ larger.Superimposed with theλ increasing effect of the regenerated bubble in the corner,the collapse time decrease faster with increasing contact angle(as shown in Fig.8).

Meanwhile, the jet velocity mode is affected by surface wettability. The more hydrophobic the surface is, the farther the bubble is from the concave corner. However, the effect of the distance on the growth amplitude of jet is not obvious when the initial λ is small. The reason is that a new cavitation bubble is generated at the concave corner. The growth direction of the new bubble is opposite to that of the jet(as shown in Fig.8),which reduces the growth amplitude of jet. Although a new cavitation bubble are generated when the initial λ is large,the deceleration effect of jet is weak,and the maximum velocity of jet increases significantly due to the long distance from the bubble collapsing point. In summary, the geometric effect of concave corner and surface wettability results in this jet mode together.

4. Conclusions

In this work, the pseudopotential MRT-LB model is adopted to model a single cavitation bubble in concave corner, and the effect of solid surface wettability and geometry on cavitation is investigated. It can be found that the wettability of concave surface has obvious effects on the evolution of cavitation bubble. When the concave surface is hydrophobic,it affects the evolution of cavitation bubble significantly on the density field,pressure field,collapse time,and jet velocity.

With the superimposed effect of surface hydrophobicity and concave geometry, the cavitation bubble collapse is accelerated. The stronger the hydrophobicity of concave is, the more significant the acceleration effect is. It is worth noting that it is easier to generate new cavitation bubble in the hydrophobic concave, which may lead to subsequent persistent cavitation. In addition,both the hydrophobicity of surface and the concave geometry bring positive effects to λ increasing.And the λ increasing effect not only accelerates the cavitation bubble collapse, but also increases the maximum jet velocity. So, we can conclude that the hydrophobic concave can enhance the cavitation effect.

On the other hand, we find that the mechanism for the effect of hydrophobic concave on cavitation bubble collapse can be directly and effectively analyzed and explained in the framework of the pseudopotential LBM.As a valid tool to simulate the cavitation bubble,LBM plays an important role in the study of cavitation bubble collapse mechanism.