可重复使用运载器多约束鲁棒预测校正制导
2021-05-06都延丽唐明明王玉惠
都延丽, 刘 武, 唐明明, 王玉惠
(1. 南京航空航天大学航天学院, 江苏 南京 211106;2. 南京航空航天大学自动化学院, 江苏 南京 211106)
0 引 言
可重复使用运载器(reusable launch vehicle, RLV)能够多次往返于天地之间运输载荷,在军事及民用航天领域越来越受到关注,其制导与控制技术代表了未来空天运输系统的发展方向[1]。然而,RLV再入过程中存在诸多复杂约束,如制导终端约束,热流密度、动压、过载等过程约束,禁飞区、航路点等地理约束,倾侧角约束,同时还须考虑再入参数不确定性,这些问题对RLV的再入制导系统设计提出了严峻的挑战。
针对过程约束等常规约束,通常采用预先设置约束走廊对阻力加速度或倾侧角进行限制的方式[2-4],以使飞行器不突破再入约束,保证再入过程的安全性。例如文献[2]将过程约束转化为阻力-能量走廊,通过设计标称阻力加速度剖面,并利用其二阶导数得到倾侧角幅值。Lu[3]提出统一适用的再入预测校正制导方法,较好解决了轨迹高度震荡和过程约束问题。标称轨迹与优化算法的结合也被用来解决此类问题,如凸优化算法[5-6]等方法被应用于再入轨迹的在线规划与跟踪,但是优化算法的引入同时也增加了系统调参的复杂性。
对于地理约束问题,如航路点、禁飞区等,快速生成满足该约束的再入轨迹并对其进行跟踪是研究思路之一[7-9]。高斯伪谱法[10-11]作为再入制导的热门方法被广泛研究,其与预测校正法结合的混合制导也成为解决此类问题的一种思路[12]。人工势场法[13-14]、虚拟触角探测[15-16]等机器人避障领域的算法被应用于再入制导实现禁飞区的规避。Wang等[17]将禁飞区和航路点转化为一系列参考点,采用模糊逻辑在参考点间寻找合适的倾侧角翻转位置。文献[18]通过定义航路点的航迹方位角可达域和控制集,给出满足航路点约束的倾侧角翻转策略,并进一步将其应用于末端方位角约束[19]。虽然上述方法在解决地理约束问题上较为有效,但是再入环境复杂多变,当存在一定程度的参数不确定时,飞行器的机动能力会受到很大影响,可能无法满足地理约束,甚至影响再入任务的完成。
关于参数不确定性的鲁棒制导问题,基于标称轨迹的跟踪优化方法多采用神经网络[20]、干扰观测器[21-22]等方法来在线估计不确定性。而预测校正制导方法对初始误差不敏感以及较高的制导精度等优越性令其在鲁棒制导研究领域具有广阔前景。根据测量到的升阻力对气动参数进行修正是增强系统鲁棒性的一种方法[3,23-24]。文献[25]通过渐消记忆最小二乘法建立环境参数预测模型,对其进行在线估计和修正,基于在线环境参数模型进行落点预测,以克服扰动对制导精度的影响,增强了系统的鲁棒性。但是,尽管在可以修正气动参数的情况下,飞行器实际升阻比的改变仍导致其纵程和横程能力都受到影响,因此还需要进一步对制导指令进行调整。
同时,考虑控制系统的执行能力,有必要对倾侧角的翻转速率进行约束,但一般方法仅对制导系统输出的倾侧角幅值指令施加限制[4],并未将速率约束转化到预测校正过程之中。另外,从制导的验证模型来看,大多数文献采用体积小、质量轻、侧向机动能力强的CAV-H模型[7],但是RLV作为运载工具,其体积和质量较大,侧向机动能力偏弱,横向制导难度较大,因此有必要针对中大型RLV模型来验证复杂多约束条件下的再入鲁棒制导算法的有效性。
基于以上分析,本文选择具备完整横侧向气动参数数据的HORUS-2B[26]作为验证模型。以预测校正制导方法为基础,利用改进准平衡滑翔条件将常规约束转化为倾侧角幅值约束,并进行了如下创新工作。
(1) 提出了一种基于二分法快速迭代搜索满足航路点约束的倾侧角翻转策略,在此过程中将倾侧角最大翻转速率约束转化为关于能量变化的速率约束,参与预测校正的计算过程;
(2) 为了进一步增强制导系统的鲁棒性,在考虑再入参数不确定的情况下,提出了基于标称升阻比和剩余能量剖面自适应调整迎角和横程误差走廊的鲁棒制导策略;
(3) 通过充分的仿真验证了所提出方法在中大型RLV模型上的可行性和实用性。
1 问题描述
考虑地球自转的影响,建立RLV的三自由度无量纲化制导方程[3]如下:
(1)

(2)
式中,ρ表示大气密度;Sref是机翼表面积;m为飞行器质量;g0=9.8 m/s2是地球重力加速度;CL和CD分别代表升力系数和阻力系数,其值与迎角α(再入制导的另一控制量)和马赫数相关。
在此基础上,参考文献[3]引入能量变量e(e=1/R-V2/2),e对无量纲时间τ的导数为
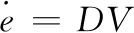
(3)
同时引入待飞航程s关于能量的导数:
(4)
式中,s表示飞行器当前星下点位置(θ,φ)到目标点星下点位置(θf,φf)之间的大圆弧长度。进一步将式(1)转化成关于能量e的无量纲方程[3]为
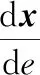
(5)

2 再入约束及其转化
2.1 过程约束及其转化
再入过程中RLV主要受到热流密度、过载、动压的过程约束以及平衡滑翔条件的限制。过程约束[3]具体形式如下:
(6)

常规的平衡滑翔条件对于再入问题来说要求过于严苛,有可能造成RLV热流约束段轨迹有比较严重的震荡。为抑制震荡,采用改进的平衡滑翔条件[27](modified quasi-equilibrium glide condition, MQEGC),具体形式为

(7)

(8)
式中,Rcrd=R0+hcrd;hcrd和Lcrd分别为当前速度V对应的再入走廊下边界高度和升力加速度。
2.2 航路点约束、终端约束和倾侧角速率约束
航路点约束可以描述为再入过程中RLV需要通过的某些特定的经纬度点,以进行载荷释放、对地监测、技术验证等特殊任务,即
φ=φ1|θ=θ1
(9)
式中,(θ1,φ1) 代表预先设置的航路点经纬度。
终端约束包括高度、速度与末端目标点经纬度约束,其中前两者可以转化成末端能量约束。终端约束以及倾侧角速率约束的表达式如下:
(10)
(11)

3 初始下降段制导
初始下降段的高度较高,空气稀薄,无法满足平衡滑翔条件,一般采用常值倾侧角飞行,不对制导系统进行指令校正。同时在此阶段,为使RLV快速通过热流密度段,通常以大迎角再入,从而使飞行器高度快速下降,减小总吸热量,为热防护系统减小压力。该段制导过程中会一直判断RLV是否满足平衡滑翔条件,满足此切换条件后,立刻切换至滑翔段制导,即
(12)
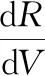
4 滑翔段多约束鲁棒制导
4.1 航路点约束的任务评估
由于航路点是预先设定的任务点,而飞行环境复杂多变,对于飞行器是否有足够的侧向机动能力完成此任务,应该给出一种简便可行的在线评估方法,因此本文将航路点任务转化为判断不等式是否成立的问题。假设存在航路点任务(θ1,φ1),当前状态点经纬度为(θ0,φ0),那么,飞行器在θ0到θ1中间某处θr倾侧角发生一次翻转后到达经度θ1处的纬度可以表示为关于翻转位置θr的函数φ(θr)。在不同的θr处发生翻转后,到达θ1处的纬度φ(θr)不同。通过对式(5)进行积分可以预测在不同翻转位置θr处发生翻转后RLV到达航路点处的纬度φ(θr),则航路点任务预测得到的纬度误差可以表示为
E(θr)=φ(θr)-φ1
(13)
在飞行器的侧向机动能力能够满足航路点任务需求的情况下,必然满足:
E(θr=θ0)E(θr=θ1)<0
(14)
如果此不等式成立,那么必定存在一个位于θ0到θ1之间的θr,使得在θr处发生倾侧角翻转时,E(θr)=0,具体分析如图1所示。

图1 不同翻转位置对航路点任务的影响
4.2 航路点侧向制导
航路点侧向制导的任务首先是确定倾侧角的翻转位置,在保证末端航向角或横程误差满足要求的同时准确通过预先设定的航路点。基于第4.1节的评估方法,可以将航路点约束转化成寻根问题。本文通过改进快速二分法迭代寻找满足要求的θr,即假设倾侧角在θ0到θ1中间的θr处翻转,那么以此侧向逻辑进行制导,当飞行器到达航路点,将使纬度误差满足
|E(θr)|≤μ
(15)
式中,μ为允许误差常数,此式即为二分法迭代终止条件,满足此条件的θr即为所求翻转点。
进一步给出迭代流程如下。
步骤 1首次确定航路点任务的倾侧角翻转位置θr,二分法迭代初始点选为当前点经度θ0和航路点经度θ1,迭代求得满足精度要求的θr。
步骤 2当需要再次校正倾侧角翻转位置时,不再直接以当前状态点作为二分法的初始点进行迭代,而是首先计算3个翻转位置θ0,θ1和θr到达航路点的纬度误差E(θ0),E(θ1)和E(θr),通过选择与E(θr)符号相反的另一个翻转点作为二分法的起始点,重新校正θr,由此可以大大减小迭代积分次数,加快系统指令的解算。
步骤 3通过判断飞行器实时经度是否到达步骤2迭代得到的翻转点θr,若到达,则进行一次倾侧角翻转,并在保证到达航路点之前,倾侧角符号不变,若未到达,则继续重复步骤2。
步骤 4判断航路点任务是否全部完成,若已完成,则进行常规末端制导,若未完成,则转向步骤1。
航路点侧向制导的下一步是确定倾侧角的符号。以再入过程的经度θ单调递增为例,在上述迭代过程下,给出倾侧角符号的确定策略为
(16)
式中,sgnz(σ)为开始执行航路点任务时的倾侧角符号;f(Z)表示横程误差走廊Z的策略函数。

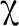
(17)

s=arccos(sinφsinφf+cosφcosφfcos(θf-θ))
(18)


(19)

(20)


(21)
然后,对于Z采用收敛的横程误差走廊:
Z=k1s
(22)
式中,k1为横程误差走廊的斜率。进一步,如果简单判断每一时刻的横程超过走廊边界就立刻进行倾侧角符号翻转,则会发生如图2所示的错误情况,横程在上一次倾侧角翻转后正在向走廊内偏转时,又进行倾侧角符号判断,导致其符号发生混乱。
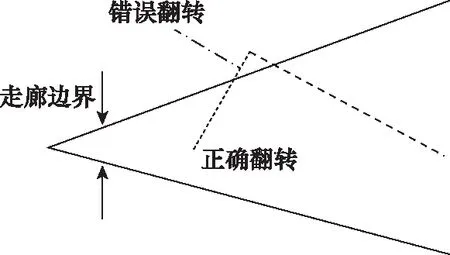
图2 倾侧角错误翻转示意图
针对此情况,本文给出翻转逻辑:

(23)
式中,pre_sgn(σ)表示前一时刻的倾侧角符号。由于在执行航路点任务期间不依靠横程误差走廊对横程进行约束,因此一般执行完航路点任务后飞行器的横程是超过走廊边界的,采用此翻转逻辑同样可以保证后续倾侧角符号不发生紊乱。
4.3 纵向制导
侧向制导已经确定了倾侧角的翻转位置和符号,纵向制导的任务则是确定并不断积分校正倾侧角的幅值。以末端待飞航程的偏差为校正准则,当再入能量e=ef时,记末端待飞航程为
f(σ)=s(ef)
(24)
只要在每一个制导周期内给定倾侧角初值σi,就可以不断对式(5)积分,积分步长为Δe,并采用割线法进行迭代,快速寻找满足精度要求的倾侧角幅值,具体迭代策略为
(25)
由于常规的线性倾侧角模型在制导周期较长时会出现倾侧角指令不连续的情况,导致控制系统的压力变大,进而影响制导精度,因此本文的倾侧角幅值模型采用文献[27]提出的二次函数模型,并使其满足式(8),可得
(26)
通过迭代寻找满足末端待飞航程精度要求的c值,则a,b的值可以由下式得到:
(27)
式中,e0和σ0为当前状态的能量和倾侧角;σf为末端倾侧角值,取值在60°~70°。在积分过程中,若航路点任务的倾侧角还未翻转,则倾侧角的符号由航路点任务的侧向制导方法确定,反之,则由式(22)的横程误差走廊确定。本文设计的考虑航路点约束在内的再入预测校正制导确定倾侧角的整体流程图如图3所示。

图3 航路点制导确定倾侧角流程图
4.4 倾侧角速率约束转化
在实际应用中,由于控制系统的执行能力有限,不能立刻在迭代得到的倾侧角翻转点进行翻转,即翻转速率有一定约束限制,如式(11)所示。此约束对航路点任务的执行精度有一定影响,而且速率限制越小,导致航路点任务的精度越差。但是若不限制翻转速率,实际姿态控制系统将很难准确跟踪制导指令。因此,本文对该约束进行了一定处理,引入到预测校正制导律当中。
预测校正制导算法通常对关于能量e的方程进行积分,故需要对式(11)进行转化。假设无量纲时间τ对时间t的转换关系为
(28)

根据式(3)和式(28)可将式(11)变换为
(29)
当需要做σ翻转机动时,其值可由式(30)确定,表示为
(30)
式中,σpre表示前一时刻的倾侧角幅值;σ(e)是用于预测校正过程中倾侧角翻转机动的数值;Δe代表预测校正的积分步长;σ(t)是实际过程中的倾侧角翻转机动值;Δt为实际的积分步长;sgn(σcmd)表示翻转机动的目标倾侧角符号。
通过以上转化,此约束可以直接应用于预测校正的过程当中。在进行步骤1~步骤4迭代时,直接考虑带有倾侧角关于能量变化的速率约束后,能够使迭代得到的翻转点更加准确,进一步提高了制导精度。另外,此转化方法不限于航路点制导,同样适用于常规预测校正制导。
4.5 再入鲁棒制导

(31)

(32)
(33)
式中,k1为走廊的斜率常数;(L/D)和(L/D)c代表实际升阻比和标称升阻比。根据不同升阻比差异调整横程误差走廊的宽度,从而保证倾侧角不会过多(或过少)地翻转,提高末端制导精度。
当升阻比减小时,飞行器的横程和纵程能力都会下降。那么在执行航路点任务时,根据上文提出的任务评估方法,可能在当前经度点θ0到航路点经度θ1之间并不存在满足航路点精度要求的翻转点θr,即式(14)不成立,则会直接导致航路点甚至再入任务的失败。通常,再入迎角的变化对升阻比有影响。本文根据HORUS-2B的气动参数模型给出了不同马赫数(Mach)下升阻力系数之比随迎角的变化关系如图4所示。

图4 升阻比随迎角的变化情况
从图4可以看出,升阻比随着迎角的减小先增大后减小,其临界点为最大升阻比迎角。为增强航路点制导系统的鲁棒性能,考虑自适应调整迎角剖面。本文首先参考文献[29]设计了基于能量的标称迎角剖面,由于再入过程中马赫数和剩余能量均为单调递减的变量,故为了描述标称迎角剖面和最大升阻比迎角的关系,将其转换在马赫数-迎角坐标系下进行对比,如图5所示。

图5 迎角剖面情况
如果直接依据升阻比差值,当升阻比小于标称升阻比时减小迎角,那么再入后期当标称剖面与最大升阻比迎角边界比较接近时,一旦调整后的迎角值小于最大升阻比迎角,则可能导致飞行器的升阻比快速降低,飞行器横程和纵程飞行能力急剧下降,反而因减小迎角造成相反的效果。
进一步地,单独以升阻比差值作为调整基准,会造成飞行器迎角的调整值过于固定,末端制导精度不高。因此,本文在此基础上引入剩余能量Se,由于能量在再入过程中为一个单调递增的量,故Se的具体形式如下:
Se=ef-e
(34)
式中,ef代表末端能量。
整个再入过程实际为一个能量耗散的过程,当迎角大于当前马赫数下最大升阻比迎角时,迎角越大,能量耗散越快,反之,能量耗散越慢。而一旦迎角小于最大升阻比迎角,则能量耗散速率的变化与上述逻辑相反。当升力减小,阻力增大时,飞行器会因为剩余能量不足,不能完成航路点任务;升力增大,阻力减小,飞行器剩余能量过多,飞行器的横程和纵程能力均增强,若不对其进行处理,则会导致飞行器飞过末端点,使得落点精度变差。基于以上分析,为了减小控制系统的压力,仅在飞行器升阻比减小(即横程纵程能力变差)的情况下对标称迎角进行调整,而对升阻比增大的情况,通过式(33)增大横程误差走廊斜率就可以消耗掉多余的能量。
根据标称升阻比和剩余能量剖面,本文提出如下迎角调整策略:
(35)
式中,Δα为迎角调整量;k2和k3是调整增益;(L/D)c和Sec为标称情况下的升阻比和剩余能量剖面。须注意的是,当调整量使调整后的迎角小于图4的最大升阻比迎角边界时,则以最大升阻比迎角飞行,不再继续减小迎角,即实际α为
(36)
式中,αc表示预先设计的标称迎角剖面;amax(L/D)表示最大升阻比迎角。
总体来看,第4部分设计了针对航路点约束的改进预测校正制导算法,同时将倾侧角翻转速率约束转化为关于能量的约束,并提出自适应调整迎角及横程误差走廊的方法以增强了预测校正制导方法的鲁棒性能。
5 仿真结果与分析
本文以HORUS-2B飞行器为研究对象[26],其初始和终端状态的设置如表1所示。

表1 初始状态和终端状态约束
5.1 倾侧角翻转速率约束下的航路点制导仿真
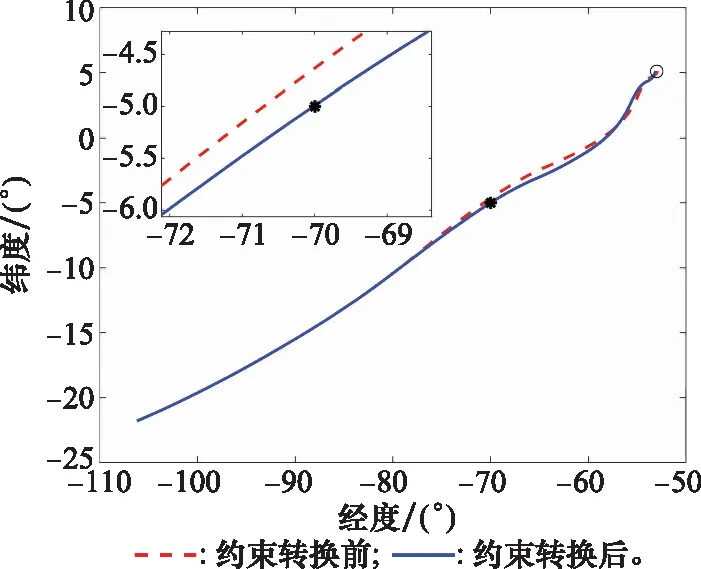
图6 倾侧角翻转速率约束下的轨迹对比

图7 倾侧角翻转速率约束下的倾侧角对比
从图6可以看出,倾侧角翻转速率约束对航路点的精度有一定影响。由于实际情况下倾侧角不能立即翻转,因此理论计算得到的倾侧角翻转位置在实际情况中已经滞后,通过应用本文提出的约束转化方法,可以在预测过程中考虑倾侧角翻转速率,将理论计算的翻转位置提前,如图7中圆圈所示。提出的方法依然保证了很好的航路点任务精度,同时也为后续控制系统的指令跟踪减小了负担,具有一定的工程实用性。
5.2 标称情况下的航路点鲁棒制导仿真
对两种极限情况下(情况1:CD+15%,CL-15%;情况2:CD-15%,CL+15%)的航路点任务进行仿真。方法1采用文献[3]中的预测校正方法,仅将其倾侧角符号确定逻辑更换为式(22)的横程走廊。由于提出的倾侧角翻转速率约束转化方法已在第5.1节验证过其有效性,因此为了单纯验证本文所提出方法的鲁棒性,对文献[3]的方法进行了改进,将倾侧角翻转速率约束的转化方法也应用于方法1。方法2即本文提出的方法。首先在飞行器横程和纵程能力最差的情况(情况1)下,对两种方法的航路点任务完成与标称情况作对比结果如图8和图9所示。从图8中可以看出,当升阻比减小导致飞行器纵程和横程能力下降时,在方法1作用下,飞行器虽然能够完成航路点1的任务,但是剩余能量已经不足以完成接下来的航路点2和末端制导任务。通过本文的调节方法,在方法2下飞行器能够较为精确地完成两个航路点任务和最后的末端制导任务。
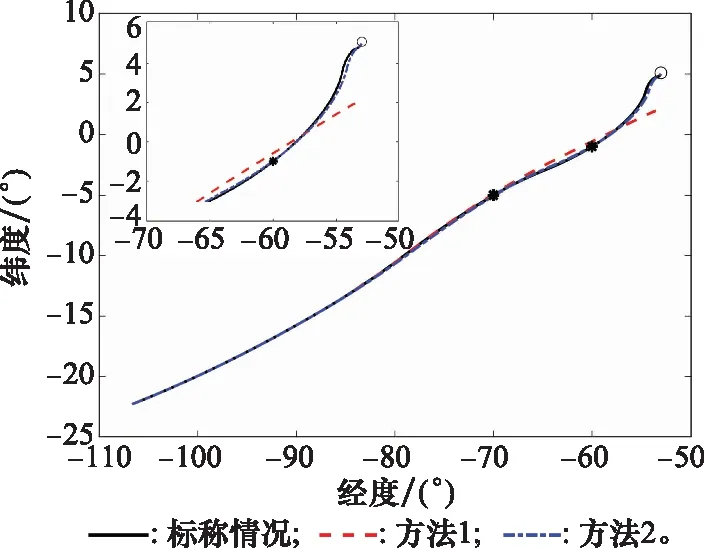
图8 再入轨迹对比情况(情况1)

图9 剩余能量对比情况(情况1)
通过本文的方法调整,从图9(情况1)可以看出剩余能量足够完成再入制导任务,并且在末端点趋近于0,满足再入任务的要求。只要飞行器横程和纵程的最短极限情况下能够有足够的剩余能量完成再入任务,那么其余情况下不会出现剩余能量不足的情况。
在情况2下,相应对应结果如图10和图11所示。

图10 再入轨迹对比情况(情况2)

图11 倾侧角对比情况(情况2)
从图10所示的再入轨迹情况来看,在情况2下,两种方法的飞行器都能够完成再入任务。当升阻比变大时,飞行器的升力增大,横程变化率加快,飞行器的剩余能量变多。如果依然采用标称的横程误差走廊,虽然航路点任务能够较好完成,但是飞行器必然需要通过更多的倾侧角翻转去消耗剩余的能量(方法1),而通过增大误差走廊的斜率,可以在航路点任务完成的末端制导阶段,通过增加横程的方式消耗能量,从而减少倾侧角翻转,减小控制系统的压力。如图11所示,在本文的调整方法下(方法2),末端倾侧角的翻转次数相比于未调整之前减少一次,但是并不影响整个制导过程的精度。
5.3 扰动情况下的蒙特卡罗仿真
为了充分模拟再入过程的随机干扰和不确定性,本文在标称情况下对一些不确定量施加符合高斯分布(3σ)的随机干扰,如表2所示。

表2 蒙特卡罗仿真的高斯扰动
由于大气密度是高度的函数,故式(6)能够转化成速度与高度相减(h=R-R0)的函数,根据此函数可确定RLV在V-h空间内的再入走廊下边界,如图12所示。
大气密度模型采用US-76标准大气模型,扰动模型采用文献[30]提出的大气密度扰动模型。在此条件下对本文制导算法进行了300次的蒙特卡罗仿真实验,具体结果如图12~图16所示。图12和图13给出了再入过程的高度-速度以及经纬度轨迹。从图上可以看出,在多种扰动条件下,飞行器能够精确完成两个航路点任务,到达预定末端目标区域,并满足预先设置的再入走廊约束。图14进一步给出两个航路点的纬度误差分布,其误差不超过±0.1°。

图12 速度-高度剖面情况

图13 轨迹情况

图14 航路点误差分布情况
从图15来看,再入过程约束也未突破,保证了制导的安全性。图16的大多数倾侧角翻转次数为5次,其中第1次为初始下降段与平衡滑翔段切换的倾侧角翻转,第2次和第3次分别为执行航路点任务的倾侧角翻转,在末端制导过程中,倾侧角翻转次数基本控制在2次以内,并且不影响落点精度。综上所述,本文提出的方法对再入过程中的不确定性具有较好的鲁棒性。

图15 约束变化情况
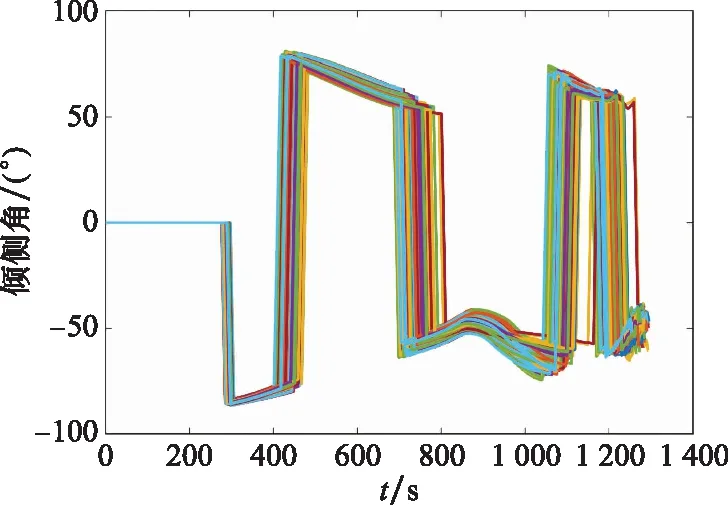
图16 倾侧角
6 结 论
本文针对RLV再入过程中存在参数不确定的航路点飞行任务,提出了一种多约束鲁棒预测校正制导方法,主要的结论如下:
(1) 针对航路点约束,提出一种航路点任务评估方法,能够将任务转化为不等式问题,通过判断不等式是否成立来对航路点任务进行评估;
(2) 基于评估方法,将航路点约束转化成寻根问题,通过改进二分法快速迭代寻找满足要求的倾侧角翻转位置,并将倾侧角翻转速率约束转化为关于能量的速率约束,在预测校正过程中进行计算,有效提高了航路点任务的精度;
(3) 考虑再入参数的不确定性问题,提出一种根据标称升阻比和剩余能量对迎角和横程误差走廊进行在线调整的方案,增强了多约束预测校正制导系统的鲁棒性能;
(4) 对提出的方法进行了充分的蒙特卡罗仿真实验,验证了方法的有效性和鲁棒性。
