基于修正滑移线场模型的倒棱刀具切削力预测

2021-05-06庄可佳浦栋麟

中国机械工程 2021年8期

庄可佳胡诚代星浦栋麟丁汉

1.武汉理工大学机电工程学院, 武汉, 4300702.武汉理工大学数字制造湖北省重点实验室, 武汉, 430070 3.华中科技大学数字制造装备与技术国家重点实验室, 武汉, 4300744.华中科技大学无锡研究院, 无锡, 214000

0 引言

金属材料实际切削加工过程表明,相较于传统尖刃口刀具，倒棱型刃口的刀具具有更佳的刃口强度和更长的服役寿命[1]。然而，倒棱会导致切削径向力和刀具后刀面磨损的激增，进而影响加工精度和刀具性能[2]。与此同时，刀具刃口尺度较小且该区域材料变形及流动情况复杂，这都使得微刃口条件下材料流动机理仍缺乏系统而深入的理论解释和试验研究。

早期学者从切削试验中发现刀具主负倒棱附近形成了稳定的材料滞留区域[3]，这一区域也被称为死区(dead metal zone, DMZ)，同时被认为是积屑瘤(build-up edge, BUE)形成的主要原因。DMZ产生的主要原因是工件材料流动受阻，负倒棱刃口对材料流动的阻碍作用会使得这一现象更加明显[4]。为了定量描述这一现象，USUI等[5]建立了接触受限刀具上的BUE模型，并采用LEE等[6]提出的滑移线方法来求解应力场、速度场以及刀具受限接触面上的摩擦因数。从此，由塑性变形理论演变出的滑移线场方法开始应用于不同的切削工况，并受到广泛关注[7]。ZHANG等[8]采用三区模型来研究DMZ对剪切角的影响，同时分析了DMZ和工件已加工表面在挤压作用下的能量损耗。在考虑BUE形成和切屑卷曲效应的基础上，FANG等[9]提出了一种改进滑移线场模型，该模型能够有效预测BUE和部分切削过程参数。KIYOTA等[10]通过控制BUE的状态，研究它在保护刀尖以及抑制毛刺和沟槽磨损方面的积极作用，并基于滑移线场方法建立了BUE状态与刀具刃口几何形状之间的定量关系。KARPAT等[11]在倒棱刀具刃前滑移线场模型基础上，根据镜像热源理论建立了倒棱刀具切削过程温度场解析预测模型。

航空零件高精度高质量加工的需求使得滑移线场模型在考虑刀具微观刃口效应的机械加工领域的应用越来越广[12]。罗翔等[13]在常规3个变形区理论基础上加入切屑和工件侧的应力过渡区域，构建了由5个变形区组成的刃口钝圆滑移线场模型。WALDORF等[14]用滑移线场方法来解释磨削加工中刚性楔状磨粒作用下的犁耕现象，推导出了考虑刀尖圆角半径的犁耕力预测模型。FANG[15]总结前人关于刀尖圆角塑性变形的研究，建立较为通用的滑移线场模型，进一步应用于微加工铣削力建模领域[16]。JIN等[17]依据滑移线场方法研究了微正交切削加工中第一、第二和第三变形区的应力变化规律，并基于Johnson-Cook材料本构模型考虑了应变率和温度变化的影响。WAN等[18]借助滑移线方法对圆刃口刀具刃前材料分离进行了研究，量化了圆角作用下的剪切和犁耕效应，并据此提出了新的微铣削力预测模型。

虽然采用有限元方法(finite-element method, FEM)建立的数值模型在切削求解时耗时较长，但有限元模型能够同时输出力、应力、应变、热传递和材料流动状态等多种复杂切削过程量，使得其相对解析模型来说更加全面和方便[19]。WAN等[20]运用有限元软件ABAQUS中的任意拉格朗日- 欧拉(arbitrary Lagrangian Eulerian, ALE)方法进行了倒棱刀具正交切削仿真，结果表明DMZ面积随切削速度增加而减小。AGMELL等[21]利用ABAQUS/Standard研究微刃口几何形状对刀具上应力分布的影响，结果表明在刀具切入时，倒棱下DMZ的形成会使刀具承受的最大主应力降低近两成。以上基于FEM的研究工作在一定程度上分析了DMZ的变化规律，但缺少对倒棱刃口条件下DMZ形成机理的分析，因此，本文从材料刚塑性变形假设着手，提出了一种适用于倒棱刃口刀具负前角切削过程的修正解析滑移线场模型。

1 基于刚塑性理论的滑移线场建模

1.1 考虑刃口微几何形状的滑移线场模型

在切削DMZ研究方面，FANG[22]采用滑移线场方法对尖刀大负前角切削时的DMZ形貌进行了建模。HU等[23]在此基础上改进得到了考虑DMZ的大负前角切削修正滑移线场模型，并通过有限元方法进行了验证。本文在以上模型基础上，进一步考虑DMZ和材料预剪区作用，提出了一种适用于倒棱刀具切削过程的修正滑移线场模型，如图1所示。

图1 倒棱刀具切削滑移线场模型示意图Fig.1 Schematic view of slip-line field model forcutting with chamfered inserts

由图1可以看出，在未变形切屑厚度(uncut chip thickness, UCT)大于倒棱刃口长度时，刀具微刃口将被切屑流完全覆盖。此时，改进滑移线场模型包含以下5个主要区域。

(1)由DEFGHC围成第一变形区，其中三角形区域DEF表示预剪切区，该区域由工件材料进入主剪切面(DC)前受切屑挤压变形所致。预剪区上表面(DE)的倾斜程度用船首角ρ表示。

(2)类三角形区域ABC为材料滞留区，即DMZ。在切削加工中，这一区域被认为是稳定存在于倒棱刃口下的刚体[24]，C点为滞止点，该点以上材料形成切屑，而该点以下材料被DMZ挤压形成工件已加工表面。

(3)直角三角形区域AHC为第三变形区，即受挤压工件材料区。该区域边界假定为绝对直线，且在死区-工件交界面(AC)上无工件材料垂直流动，即认为该区与DMZ无材料交换，交界面局部流动剪切应力可通过摩擦因数角ξ1表征。

(4)扇形区域DBC为主滑移线场，其中圆心D是应力奇异点，通过该区域，第一变形区的剪切速度逐渐滑移成为切屑流速。

(5)直角三角形区域JBI为第二变形区，该区域由摩擦因数角ξ3表征，同时该角度也可表征刀具-切屑接触面(BJ)间的滑动摩擦接触，BC为静摩擦接触面[25]。DMZ(图中ABC)与刀具倒棱面(AB)的接触由摩擦因数角ξ2表征，在DMZ稳定存在于刃口前端条件下，该角度可以表示为0°[22]。

1.2 模型表达与求解

为了保证第一变形区速度的连续性，预剪区的顶点D的上升高度应该与死区-工件接触面的上升高度保持一致，即点D到工件未加工表面的高度要等于点C到已加工表面的高度，因此船首角可通过下式计算[26]：

(1)

式中，α为DMZ下表面AC与工件已加工表面间的夹角，称为死区角；ξ1为死区-工件交界面(AC)上的摩擦因数角。

各交界面上的局部流动剪切应力与对应摩擦因数角有如下关系：

(2)

式中，τdw、τdt和τct分别为死区-工件交界面(CA)、死区-刀具交界面(AB)和刀具-切屑交界面(BJ)的流动剪切应力；k为工件流动剪切应力。

为了简化计算过程，交界面CA和BJ上的流动剪切应力可以认为相等，即ξ1=ξ3[27]。

由式(1)中假设已知变量和所得船首角ρ，可顺序推导出图1中其他滑移线场角度[28]：

(3)

通过以上角度可进一步确定图1中滑移线场各长度为[28]

(4)

式中，lsh、ldw、lcm分别为主剪切面(DC)、死区底边(CA)和倒棱面(AB)的长度；lst、lsl分别为圆弧(BC)和刀具-切屑接触面(BJ)的长度；ε、tch分别为主剪切区和切屑的厚度。

本文中假设顶点J为刀具与切屑分离点[29]，因此，刀具-切屑接触长度可以表示为静接触区BC和滑动接触区BJ的长度之和。在本模型中，通过计算得到的刀具-切屑接触长度约为未变形切屑厚度的两倍[30]。

如前所述，DMZ稳定存在于倒棱刃口下[24]，作用在刀具上的力如图2所示[27]。

图2 倒棱刀具受力分析示意图Fig.2 Force diagram of chamfered insert

作用在死区-工件交界面上的挤压力可以分成法向和切向两个组分力(FN1和F1)；作用在静接触区(弧BC)和滑动接触区(线段BJ)上的力可表示为分力FN2、F3和FN3[27]。值得注意的是，组分力FN2代表的是作用在弧面BC上的简化法向合力，而圆弧BC处为静接触，切向组分力F2忽略不计；由此，作用在刀具上的切削力Fc和进给力Ft可通过叠加各组分力得到：

(5)

其中，各组分力表示如下[31]：

(6)

其中，w为切削宽度。由于w和k这两个量都是未知的，因此本文引入量纲一的量Fc/(kw)和Ft/(kw)进行计算。

由式(1)～式(6)可以发现，由于刀具前角γ2、倒棱长度lcm和倒棱角度θcm均已知，滑移线场中其他几何参数均可以通过死区角α和摩擦因数角ξ1推导获得，所以图3所示迭代方法的目的就是在α和ξ1许用取值范围内，找出使切削力比Fc/Ft和切厚比tch/h的预测结果与输入测量结果ΔD1之间误差最小的一组角度组合：

(7)

式中，下标p、m分别表示计算预测结果和试验测量结果。

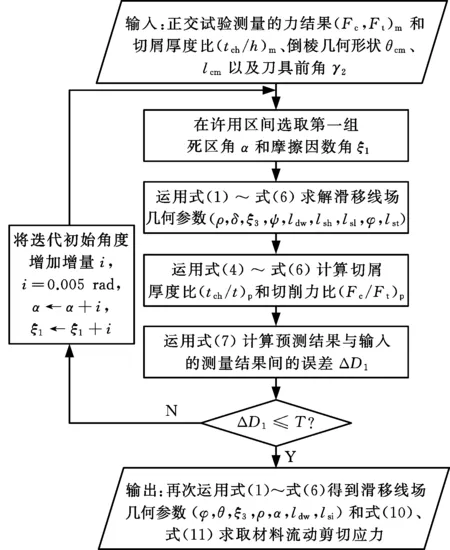
图3 滑移线场几何参数迭代求解流程图Fig.3 Flow chart of the iterative determination ofslip-line filed geometry

图3中T是公差，在本文中设定为0.5。死区角α和摩擦因数角ξ1许用取值范围通过Hill过应力准则[31]确定，即在变形区内应力线(切屑上表面)和刚性线(图2中DB)的夹角η需在限定范围以避免过应力。则有

(8)

其中，η为偏转角度，该角度在π/4到3π/4之间变化；pD为刚性顶点D处的静压力，可通过下式求解[17]:

pD=k(1+2θ+2δ)

(9)

在确定了死区角α和摩擦因数角ξ1之后，其他滑移线场角度均可以根据式(1)～式(4)求解，联立式(2)、式(5)、式(6)可以反求出材料流动剪切应力：

(10)

(11)

在计算结果中k1和k2有少许误差，为减少误差取平均值，即k=(k1+k2)/2。

2 滑移线场模型验证

2.1 有限元仿真设计

为了验证所提出的修正滑移线场模型的合理性，采用有限元仿真软件DEFORM-2D/3D进行切削仿真[32]。具体而言，设定工件材料为304不锈钢、刀具材料为硬质合金；改变刀具倒棱刃口几何形状和切削工况参数，提取仿真结果中的切削力和切屑厚度数据，按照图3所示的求解流程进行迭代求解；对比仿真滑移线场角度、DMZ等结果与对应模型预测结果，验证修正滑移线场模型的适用性。

正交切削有限元仿真参数见表1。切削宽度w=2.5 mm和切削速度vcu=100 m/min保持不变，刀具前角设计为-7°以贴近实际切削加工[33]。

表1 切削仿真参数和切削力结果Tab.1 Parameters of cutting simulations andcutting force results

为了显示倒棱刃口的加入对刀具切削加工的影响，表1中加入了一组倒棱角为0°的参数，编号为0，即尖刀负前角切削。各组仿真得到的切屑厚度tch、切削力Fc和进给力Ft结果也在表1中对应列出。

2.2 模型验证与仿真结果讨论

将表1的后三列数据处理为切屑厚度比和切削力比，按图3所示的方法迭代，结果如图4所示。

图4 切削力比和切屑厚度比的预测值和仿真值Fig.4 Values of results of predictions and simulationsof cutting force ratio and chip thickness ratio

由图4可以看到，预测值与仿真值误差较小。误差主要体现在切削力比的预测，而且迭代预测切削力比小于仿真切削力比，造成这一现象的原因在于滑移线场模型的刚塑性变形假设未考虑材料应变硬化和热软化等作用。相比之下，切屑厚度比的预测结果与仿真结果匹配度很高，这说明本文所提出的滑移线场模型在材料流动几何参数和切屑形态预测方面具有很高的准确性。

图5给出了仿真测试编号1所对应工况下的仿真速度场结果。图中红色线条为根据速度场提取出的仿真滑移线场轮廓。可以看到，在倒棱刃口下方出现了深蓝色类三角形区域，即死区，并且其左侧边界呈现出本文模型预期的圆弧状，死区下边界也与水平线成一定夹角(图5中α)。

图5 仿真速度场举例(仿真测试编号1)Fig.5 An example of simulated velocity contours(simulation test 1)

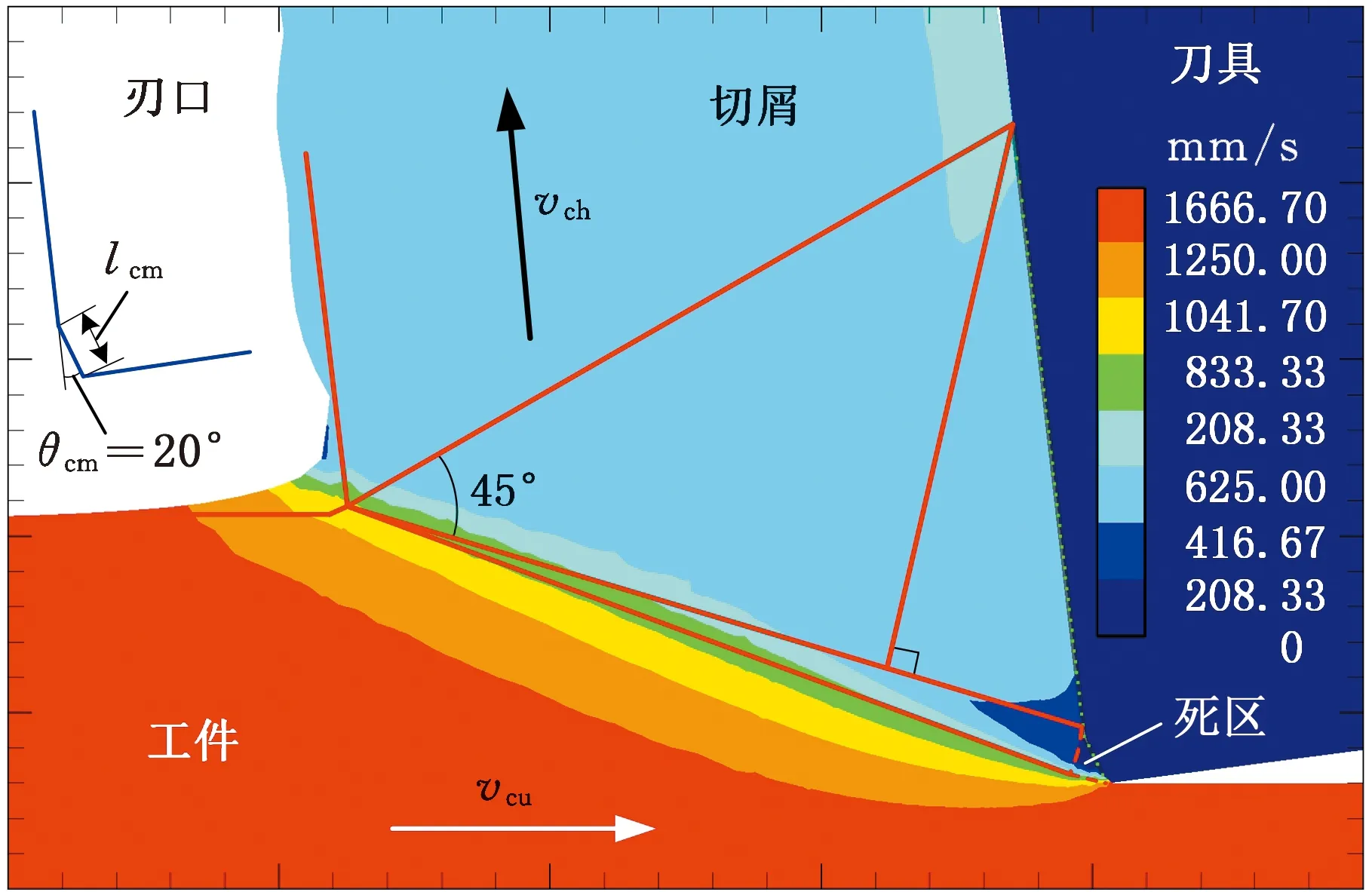
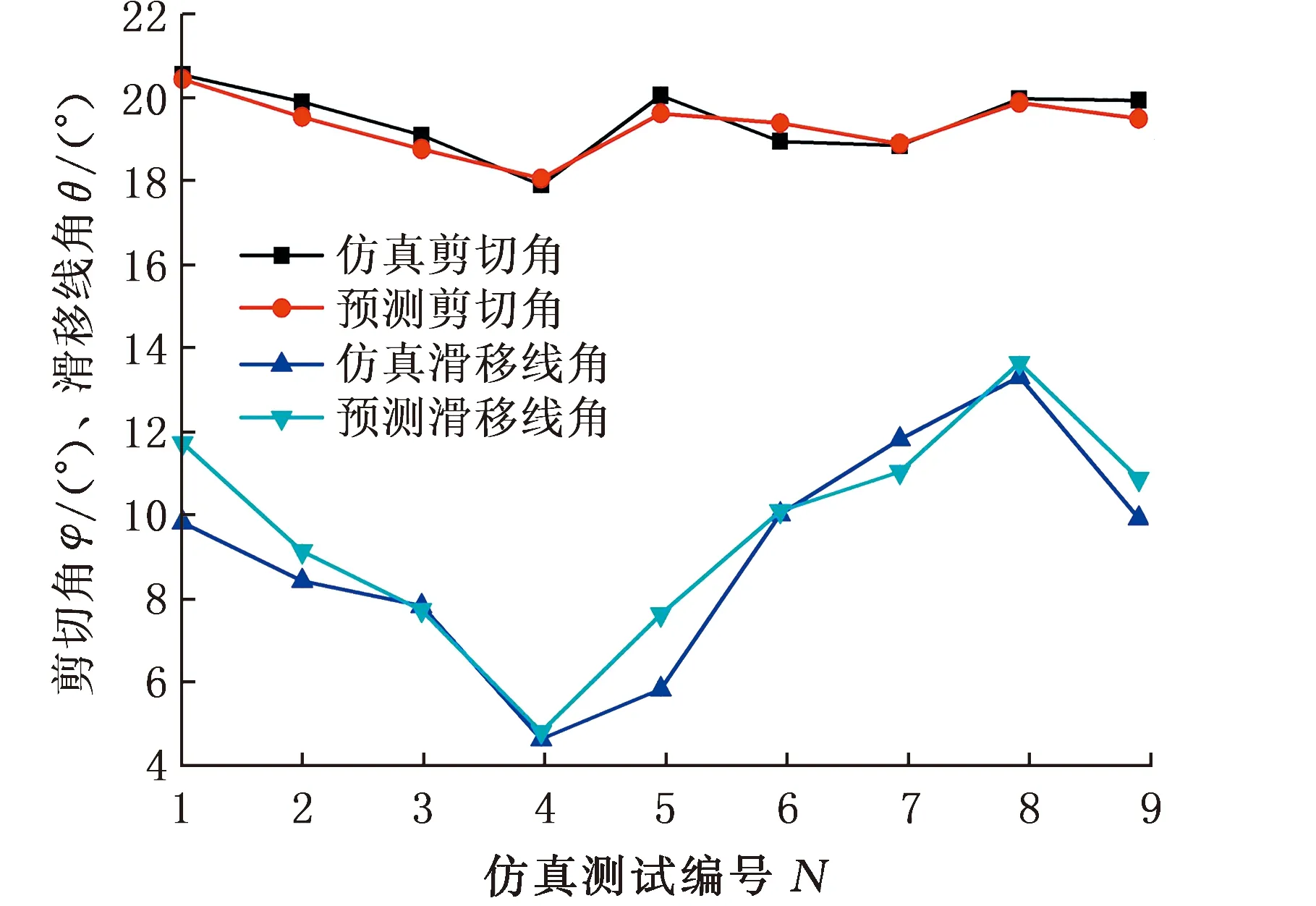
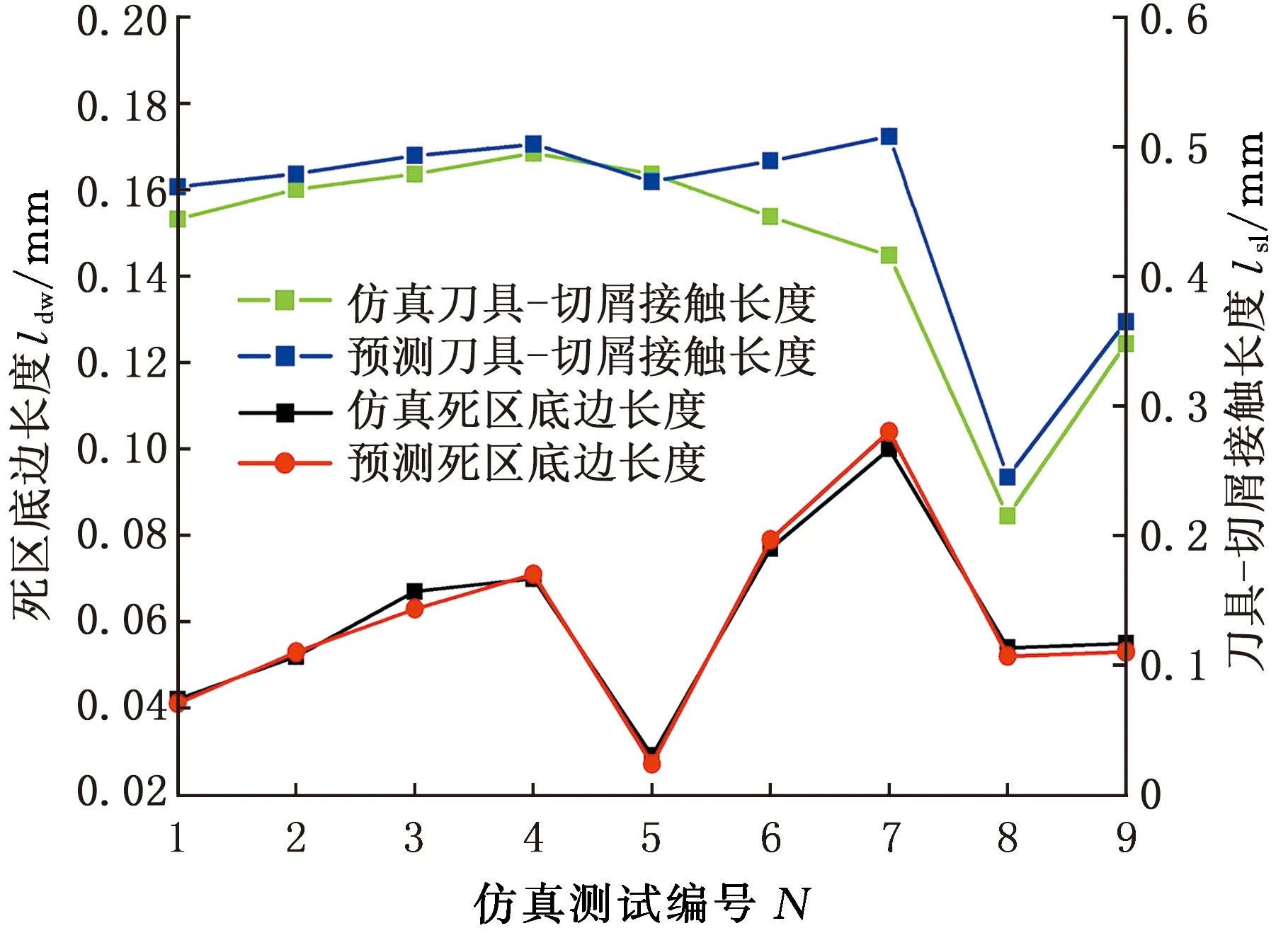
为了进一步验证所提出的滑移线场模型在预测刃前材料流动状态的可靠性，还提取了不同倒棱角度、倒棱长度和切削厚度作为仿真条件的速度云图对模型进行验证(图6～图8)。按照图5所示滑移线场辨识方法，在仿真速度场云图上添加辅助滑移线，将图6～图8仿真结果中包括剪切角、滑移线角、死区角、船首角以及死区在内的详细滑移线场几何参数提取出来，并与模型预测结果进行对比，结果如图9所示。

由图9a可知，随着倒棱几何形状和切削厚度的改变，滑移线角呈现明显的波动，而剪切角变化相对平稳，主要集中在18°～21°之间。图9b中，对于编号1～7的变倒棱刃口几何形状工况，仿真结果中船首角、摩擦因数角和死区角的波动幅度分别为2.5°、6.5°和4.5°，由此可见摩擦因数角和死区角相对船首角受刃口几何形状影响更加明显，这说明倒棱刀具刃口对第二变形区和第三变形区的影响明显大于对第一变形区的影响。由图9c可以发现，在变倒棱长度(即仿真测试编号5、2、6和7)工况下，刀具-切屑接触长度预测值与仿真值有较大差异，尤其是对于仿真测试编号6和7，仿真接触长度呈现递减趋势，而预测结果却在递增，这一现象可归结于模型中的死区顶点与倒棱顶点重合假设(图1中的B点)，因此当倒棱长度增加，由于自由应力边界存在，模型预测刀屑分离点位置会急剧上升，而仿真得到分离点却增加缓慢，从而使得仿真值比预测值小。但整体来看，9组仿真中DMZ与解析模型迭代预测值大多匹配良好。

3 倒棱刀切削力预测模型

3.1 仿真滑移线场几何参数分析

图9可以进一步拆解为变倒棱角度、变倒棱长度和切削厚度的滑移线场几何参数变化。为便于叙述，此处以倒棱角和倒棱长度影响下的滑移线角和摩擦因数角变化为例。

从图10和图11中可以发现，在给定变化范围内，滑移线角和摩擦因数角均随着倒棱角度、倒棱长度以及切削厚度的变化表现出较明显的线性变化趋势，且拟合直线与原预测结果的相关系数均在97%以上。同时还发现，滑移线角与倒棱角度成正相关，而与倒棱长度成负相关，这是因为倒棱面的高度直接影响DMZ的左边界(弧BC)的长度，从而影响滑移线角；相反，摩擦因数角随着倒棱角的增大而增大，根据摩擦因数角与摩擦因数的关系[22]：

(a)仿真测试编号1(θcm=10°)

(b)仿真测试编号2(θcm=20°)

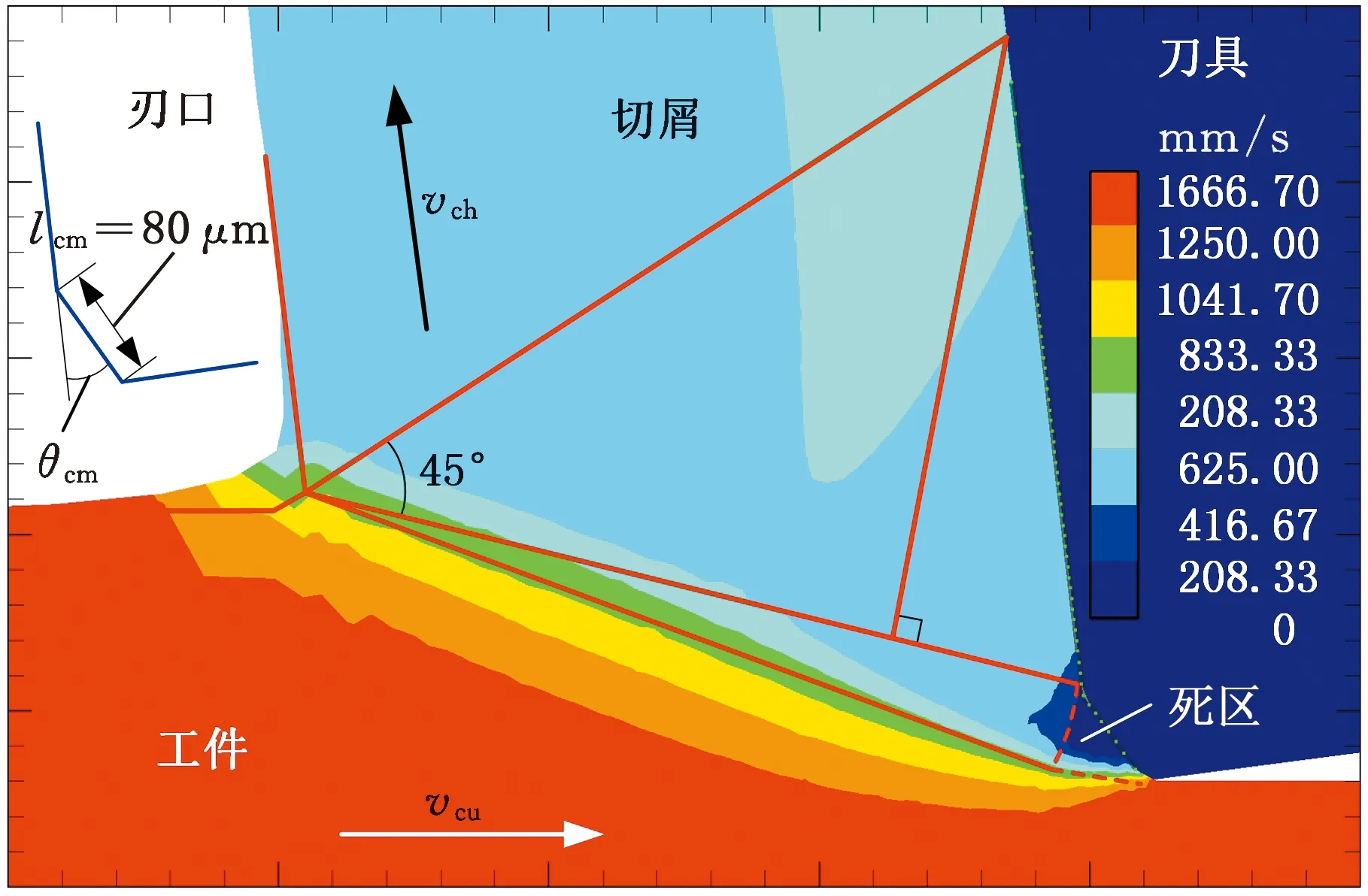
(c)仿真测试编号3(θcm=30°)

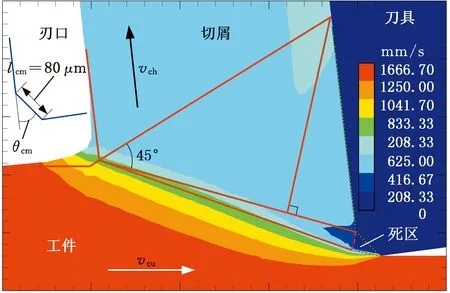
(d)仿真测试编号4(θcm=40°)图6 变倒棱角度仿真死区附近速度场(lcm=80 μm,h=0.2 mm)Fig.6 Simulated velocity contours near DMZ withvarying chamfer angles(lcm=80 μm,h=0.2 mm)

(a)仿真测试编号5(lcm=40 μm)

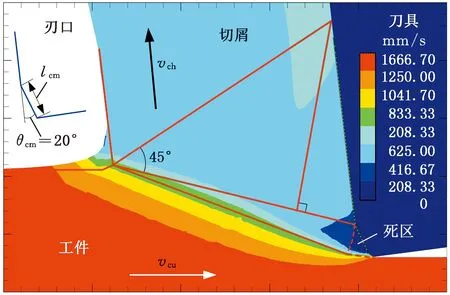
(b)仿真测试编号2(lcm=80 μm)

(c)仿真测试编号6(lcm=120 μm)

(d)仿真测试编号7(lcm=160 μm)图7 变倒棱长度仿真死区附近速度场(θcm=20°,h=0.2 mm)Fig. 7 Simulated velocity contours near DMZ withvarying chamfer lengths(θcm=20°,h=0.2 mm)

(a)仿真测试编号8(h=0.1 mm)

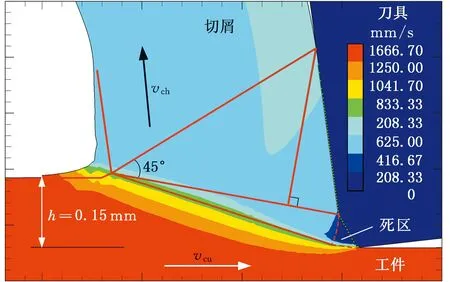
(b)仿真测试编号9(h=0.15 mm)

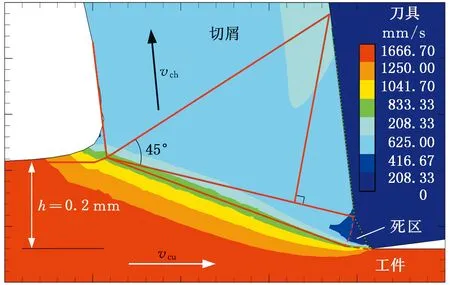
(c)仿真测试编号2(h=0.2 mm)图8 变切削厚度仿真速度场(lcm=80 μm,θcm=20°)Fig.8 Simulated velocity contours with varying UCTes(lcm=80 μm,θcm=20°)

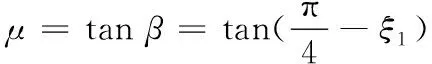
(12)

可以知道界面间的摩擦因数也随之增大。这可能是由于随着倒棱面高度降低，刃口下滞留的材料减少，死区-工件交界面的挤压作用随之减小。而随着倒棱长度的增加，滞留材料变多，挤压作用增加，摩擦因数增大，从而导致摩擦因数角减小。值得说明的是，其他滑移线现场几何参数也有此规律。

(a)剪切角和滑移线角

(b)死区角和摩擦因数角

(c)死区底边和刀具-切屑接触长度图9 部分滑移线场几何预测与仿真结果对比Fig.9 Comparison of some slip-line field geometriesfrom predictions and simulations

图10 滑移线角和摩擦因数角随倒棱角度变化Fig.10 Slip-line angle and friction factor angle withvarying chamfered angles

图11 滑移线角和摩擦因数角随倒棱长度变化Fig.11 Slip-line angle and friction factor angle withvarying chamfered lengths

3.2 正交切削力预测

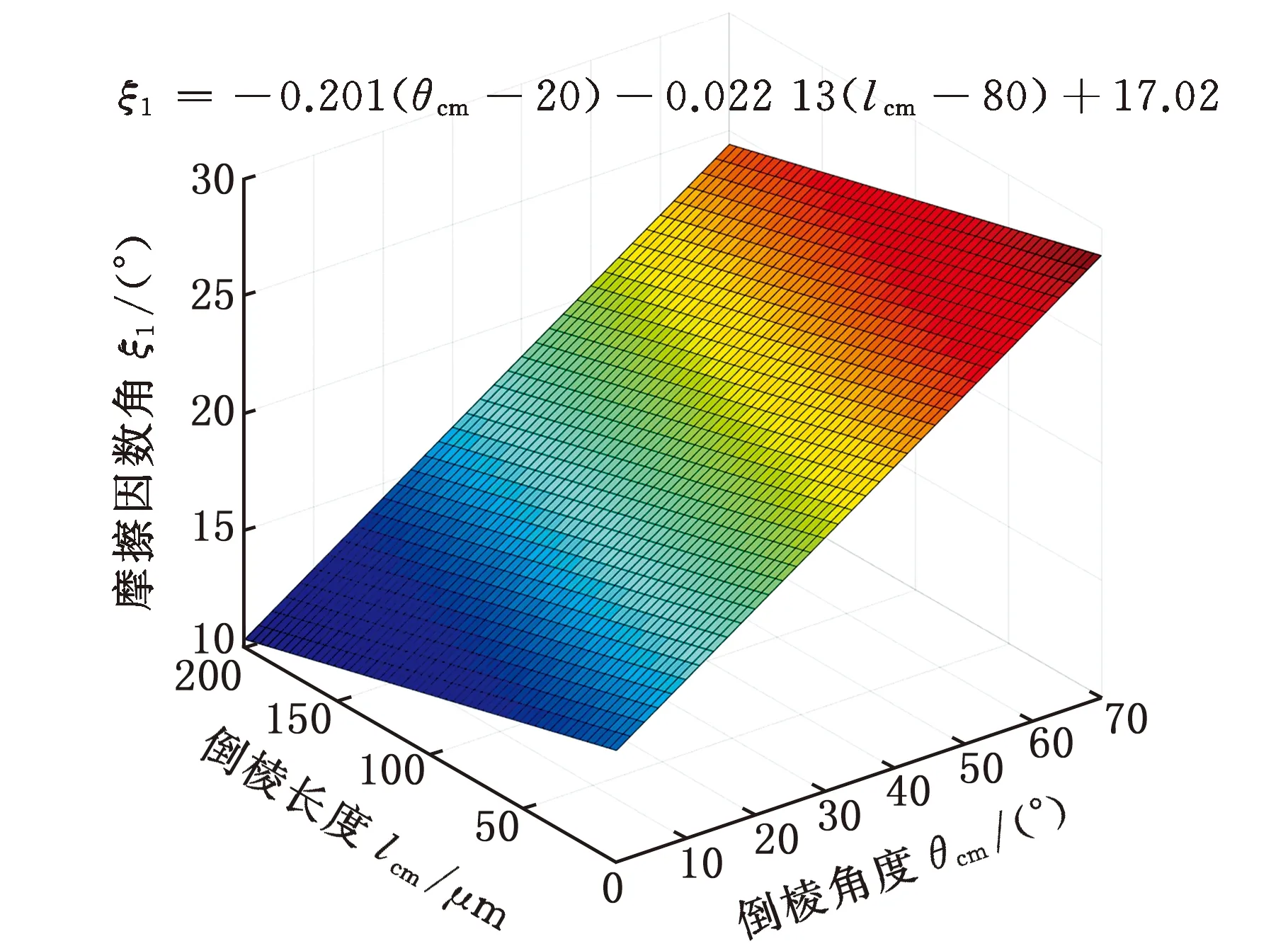
在4.1节推导的线性表达式的基础上，本节通过空间平面求解方法，得到滑移线角和摩擦因数角与倒棱刃口几何形状的对应平面，如图12所示。通过滑移线角和摩擦因数角即可由图3中的迭代方法推算出整个滑移线场，进而可以计算切削力。

图12a显示在倒棱角度大于53°且倒棱长度小于65 μm时，计算得到的滑移线角为负值(图中未显示负值)，这说明在小倒棱长、大倒棱角情况下，刃口区域材料流动不符合滑移线场方法的刚塑性变形假设，此时本文提出的滑移线模型不适用，但是在图中显示区域，仍可以通过上述方法，获得不同倒棱刃口下的滑移线场。

(a)滑移线角

(b)摩擦因数角图12 滑移线角和摩擦因数角与倒棱几何形状对应关系Fig.12 Determined correlations of both slip-line angleandfriction factor angle with chamfer geometries

图13 不同条件下模型预测材料流动剪切应力变化Fig.13 Variation of the predicted material shear flowstresses in different cutting conditions

图13给出了9组仿真结果各自迭代求得的304不锈钢材料的流动剪切应力，可以看到模型预测值随着切削条件改变而在525～570 MPa区间内波动变化，为了简化后续求解过程，本文取9组仿真结果的平均值k=545 MPa作为工件材料的流动剪切应力，即可在前述滑移线场的基础上，结合材料流动剪切应力确定该条件下的切削力。

4 切削试验验证

4.1 正交试验设计

为验证所提出的倒棱刀具正交切削力预测方法的准确性，设计了正交切削试验，试验台如图14所示。

图14 正交切削试验台Fig.14 Set-up of the orthogonal cutting experiment

圆柱工件材料为304不锈钢，其前端设计成直径120 mm、宽度2.5 mm的栅格。刀具选用三角形硬质合金，其型号为TCMT110204，刀杆型号为STCCR2020K11，并具有-7°前角，二者被定制夹具固定在Kistler9257B三向测力仪上。数控车床型号为CAK5085nzj，切屑厚度通过KEYENCE VHX-100超景深三维立体显微镜测量获得。试验选用刀具刃口具有4种配置，均通过Alicona Infinite Focus G5三维表面测量仪确定(图15)。

图15 倒棱刃口图像及几何形状测量结果Fig.15 Image of chamfered edge and measuredgeometry results

4组切削试验参数如表2所示，试验时切削速度为100 m/min，进给量为0.2 mm/r，切削宽度(即栅格宽度)为2.5 mm，所有试验均为干切条件，且每组工况均包含2次重复，试验测量结果为3次试验取平均值。

表2 正交切削试验设计Tab.2 Design of orthogonal cutting experiments

4.2 试验结果对比与讨论

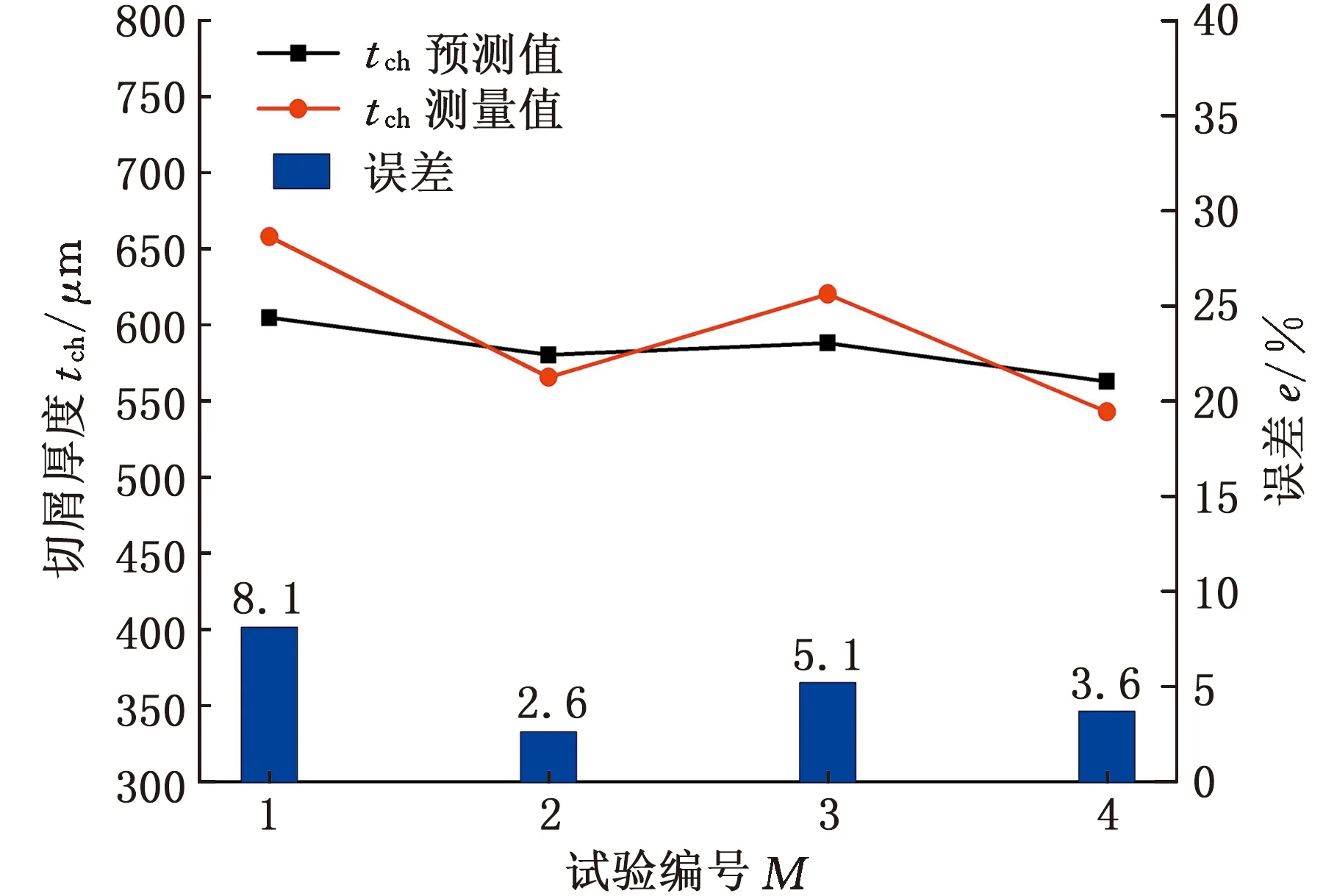
根据推导得到的滑移线场与倒棱刃口的对应关系以及计算出的304不锈钢材料的流动剪切应力，输入表2中的试验参数(刃口几何形状和切削工况)，得到了切削力和进给力以及切屑厚度的预测值，并与对应试验测量值进行对比，见表3和图16。

表3 切削试验测量结果与模型对应预测结果Tab.3 Results from cutting experiments and predictions

(a)切屑厚度

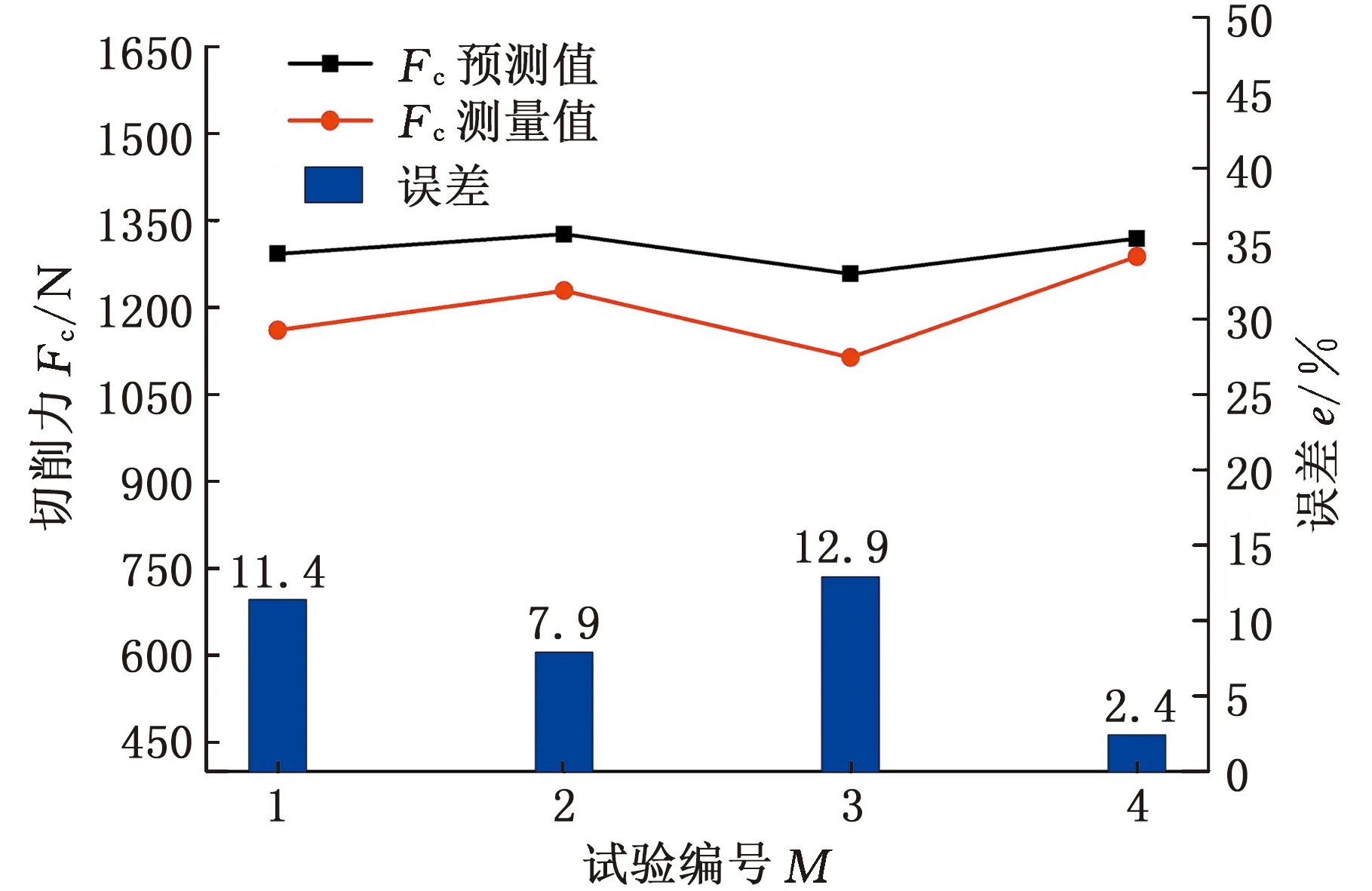
(b)切削力

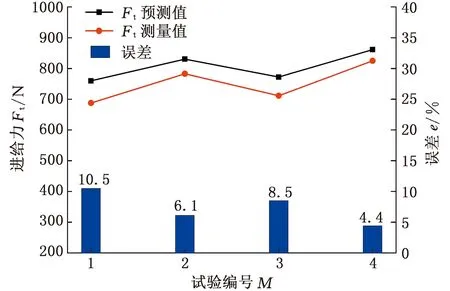
(c)进给力图16 切削试验测量结果与模型预测结果对比Fig.16 Comparison of obtained results from cuttingexperiments and predictions

由图16可以看出，模型预测值均与试验测量值吻合良好。图16a中，切屑厚度的平均预测误差为4.9%，随着倒棱角度和倒棱长度的增加，切屑厚度均有所减小，这主要是因为DMZ面积在增大，倒棱处滞留材料增多，使得更多材料被挤压进入工件已加工表面，流入切屑部分减少。图16b中，预测切削力均高于测量结果，这可能是由于在较低切削速度下，刀具刃口处容易形成BUE，从而使得刀具前角增大，切削力下降。在图16c中，进给力测量值也比预测值小，造成这一现象的原因是实际切削加工中切屑存在卷曲效应，使得刀具-切屑接触长度较模型预期更短，同时BUE未能被及时带走，减缓了DMZ下材料挤压进程。