CUPT 2019循环摆研究

2021-05-06钟粤文刘姝含孙宇飞

物理与工程 2021年2期

钟粤文刘姝含孙宇飞房毅

(华东理工大学理学院,上海 200237)

“循环摆”描述了一个在生活中常见却物理原理深刻的现象:将一重一轻两个物体通过水平杆上的一根绳子相连,并拉轻物以吊起重物。释放轻物,它将绕着杆转动,从而阻止重物载落到地面。生活中习以为常的现象,但其中的物理原理仍停留在猜想阶段,鲜有人去探究各参量对其的影响。笔者通过对三大中文文献数据库以关键词“循环摆”为题名,进行检索,只有一篇命中。该文“探究循环摆各变量对环绕圈数的影响”[1]研究性不够。此前部分视频网站上也曾演示过循环摆,但只是从能量的角度泛泛而谈,而对隐藏在现象背后的物理原理却未作探究。本文将以实验与理论相结合的方式,探究循环摆现象。

1 理论分析

所谓循环,指的能够旋转一周以上,因此本文中对循环摆的约定是:如果m(本文公式中的m代表轻物体的质量,叙述中的m指的是轻物体,下同,略)最终能绕杆旋转一圈以上,则认为形成了循环摆(见图1)。实验观测发现:当m到达最高点时M(本文公式中的M代表重物体的质量,叙述中的M指的是重物体,下同,略)还在运动的情况,没有出现。且如果m能越过最高点,则可绕杆一圈以上。

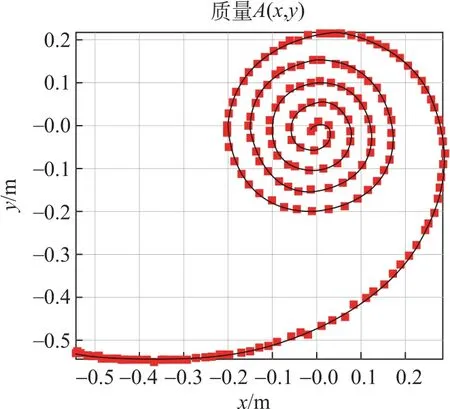
图1 循环摆m 的运动轨迹

由以上实验事实,我们可以认为m在第一次到达最高点之前就已经进入渐开线运动,因此可以将m的运动轨迹分为两部分,第一部分为M停止运动之前(即m做循环摆运动);第二部分为M停止运动之后(也就是m做渐开线运动)。本文中将第一部分运动结束、第二部分运动开始时的时刻称为临界时刻。渐开线的数学形式已经很清晰,根据临界时刻的各个物理量,运用能量守恒也很容易写出第二部分的运动方程,因此本文着重探究m第一部分的运动。

记连接m和杆的那段绳子长度为l,与杆的切点为P;连接M和杆的那段绳子与杆的切点为Q;Pm与水平面的夹角为θ(逆时针为正,顺时针为负);杆的圆心为O;两切点与圆心连线的夹角为ψ;绳子与杆的摩擦因数为μ;杆半径为r;M运动的速度为vM;Pm段绳子的张力为Fm;QM段绳子的张力为FM;沿mP指向P的单位矢量为eτ,将eτ顺时针旋转记为矢量eφ(显然eτ,eφ随着m位置的变化而改变);重力加速度为g。为表示清晰,图2中将杆的比例放大,但事实上,杆半径一般在0.004～0.01m 之间,而释放轻物时的l一般在0.5～1.1m 之间。

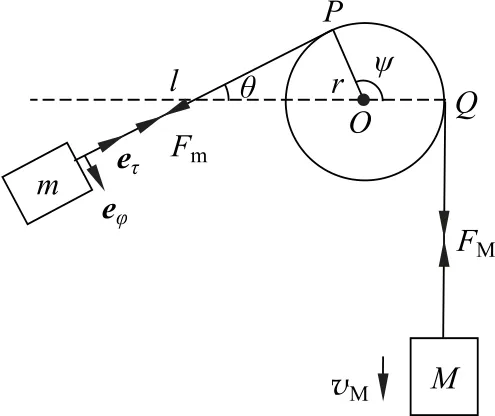
图2 运动分析图

先对题目进行简单的分析,可以看到M应该是做直线运动,对应的运动方程应该较为简单,而m做二维运动,如果通过极坐标来描述的话,需要同时建立θ和l所满足的方程式,根据绳子是刚性的这一条件,可建立l与M的方程。

然而θ所满足的方程,较难得出,也是本文的重点。面对这样复杂的物理问题,通常先假设摩擦因数为μ=0,由此写出系统的拉格朗日量,然后根据拉格朗日运动方程来求解。再考虑μ≠0时,对有耗散情形的修正。但是,作者通过尝试,发现这种思路反而使问题无法分析。因为在μ=0的条件下,不会出现临界时刻。究其原因,不难发现:如果μ=0,M加速度和速度同时为0 的时刻不会出现,因此M不会停止运动,而是往复运动。同时,连接m与杆的那段绳子,也不能保证一直处于拉直状态。

如何描述θ所遵循的物理规律,笔者运用叠加原理,将任一时刻m的运动看作重力场中:m作渐开线运动与以P点为瞬轴的“定轴”转动的合成。由此可将所满足的规律看作由三部分加速度叠加而成:与重力相关部分、与渐开线相关部分、与绕瞬轴“定轴”转动相关部分。为此,笔者在1.1.2节分析过程中,分别分析上述3种因素对的贡献,基于叠加原理,得到循环摆所满足的方程。这一方程正确性在随后的实验中也得到了进一步证实。

1.1 分析临界时刻前m 的运动[2,4,5,7]

在实验中,鉴于m的形状;空气阻力和绳子质量对系统的影响甚小,因此在推导中将其忽略。

1.1.1的表达式

首先,根据几何关系可得ψ=+θ,代入绞盘方程[2]可得

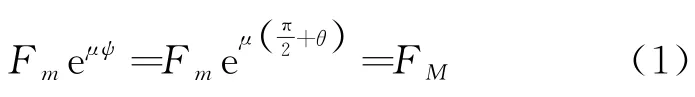
对M应用牛顿第二定律可得

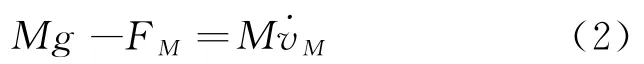
将m的加速度在eτ和eφ上分解,因为绳子只能提供eτ方向的拉力,任何时刻P点都为m的瞬心,m对P点的角速度为,所以在eτ方向上有

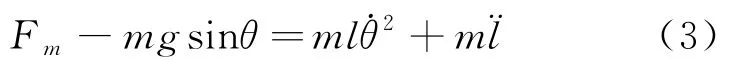
上式左边为m在eτ方向所受的合外力,右边第一项为沿eτ的速度方向改变产生的加速度,右边第二项为沿eτ的速度大小改变所产生的加速度。

在临界时刻之前,M不断下坠和m绕杆旋转,模型中假设绳子为理想刚性绳,因此可得式(4)

上式左边为Pm变化的速度,因为l随时间减小,所以加一个负号。右边第一项为绳子缠绕在杆上致使l缩短的速率,第二项为M向下运动致使l缩短的速率。将式(4)两边同时对时间求导,可得式(5),注意,˙l对时间求导时会出现一个负号。

联立式式(1)、式(2)、式(3)、式(5)可得式(6)

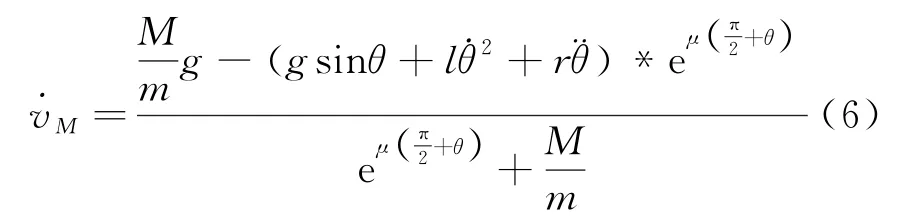
1.1.2的表达式[9-11,14]

第三部分为沿eτ方向上的平动所导致的角加速度记为β3。通过受力分析,β1的表达式容易得到

为求得β2的表达式,将β2的成因抽象成当质点做渐开线运动时的角加速度,所以首先推导渐开线运动的规律,仅考虑质点做渐开线运动引起绳长变化,质点对于瞬心的角加速度。

如图3所示选取绳长和绳子与水平面的夹角为广义坐标,则

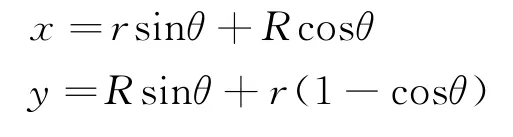
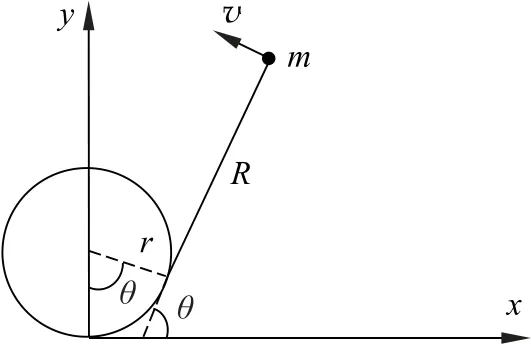
图3 渐开线运动

对t求一次导,并代入约束条件的微分形式得

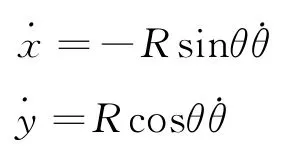
则体系的拉格朗日量为

式(9)中左边为渐开线运动所导致的角加速度,记为β2,右边出现了l,r等物理量,正是描述渐开线运动所需的物理量,体现出杆半径r对此系统的影响。而且如果让r趋向于0,则β2也趋向于0,符合实际情况

仿照β2的推导过程,推导β3:β3成因于质点绕轴旋转时,由于旋转半径改变所产生的角加速度。下面仅考虑质点旋转半径改变,质点对于瞬心的角加速度。

如图4所示选取绳长和绳子绕过的角度为广义坐标,则

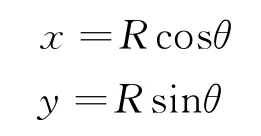
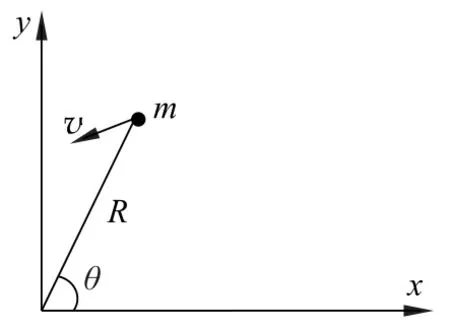
图4 “定轴”转动

对t求一次导得

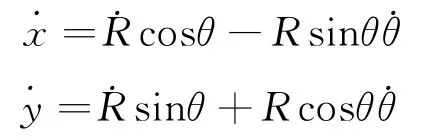
则体系的拉格朗日量为

根据我们先前的分析β3是由于m沿eτ方向的平动而产生,之所以m会沿eτ方向有平动,是因为M的拖拽,式(11)中左边出现vM这一项,反映了M的运动对m运动的影响,当临界时刻以后,M停止运动vM=0,则β3=0,于是m便在重力场下做渐开线运动了。与实验事实相符合。

因为β1,β2,β3的方向相同,因此=β1+β2+β3,将式(7)、式(9)、式(11)代入得

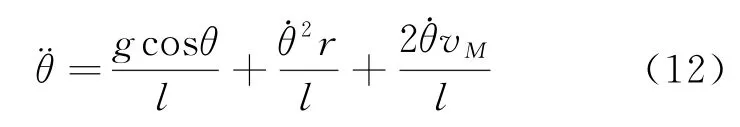
1.1.3 m 运动的微分方程组

根据1.1.1节和1.1.2节的分析所得到的式(6)和式(12)还不能构成一个可解的微分方程组,需要加上约束条件式(4),由式(4)、式(6)、式(12)所构成的微分方程组的总微分阶数为4,因此需要四个定解条件,分别为、vMt=0、θt=0、lt=0,由于是静止释放,所以=0,vMt=0=0,而θt=0与lt=0可以由实验得到,将初始时刻的θ与l记为θ0,l0。通过求解微分方程组,便可得到m运动的信息。

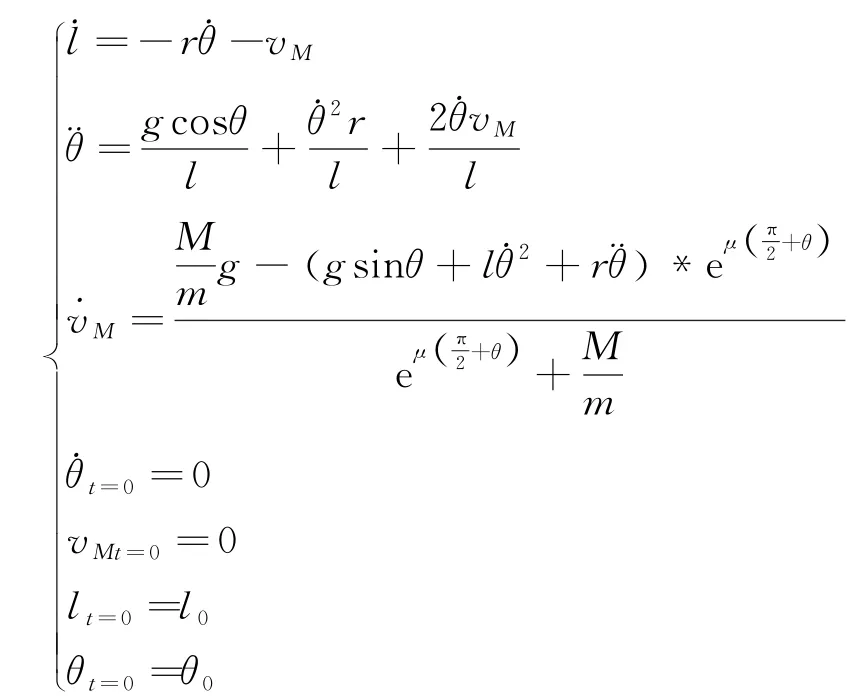
1.2 形成循环摆现象的条件

临界时刻的所有物理量均加角标“变”表示,如θ变,l变(下同,略)。由实验得到,如果m能越过最高点,则可绕杆一圈以上。因此,我们将m是否能越过最高点作为是否形成循环摆的判据。设m运动到最高处时所有物理量均加角标“最高”表示,如图5 所示,最高处的角速度为(下同,略)。

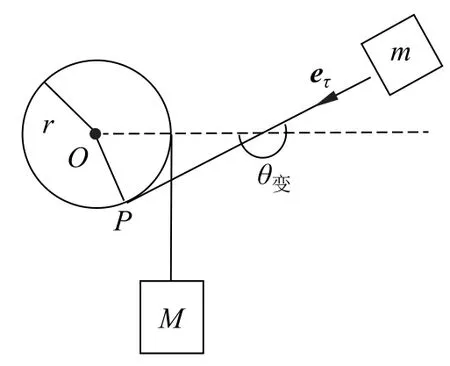
图5 临界时刻的系统状态

临界时刻过后绳子与杆不再发生相对滑动,因此体系不再有能量耗散,临界时刻过后,在重力场下m做渐开线运动,机械能守恒。以杆中心O所在高度为零势能,则临界时刻m的机械能可表示为

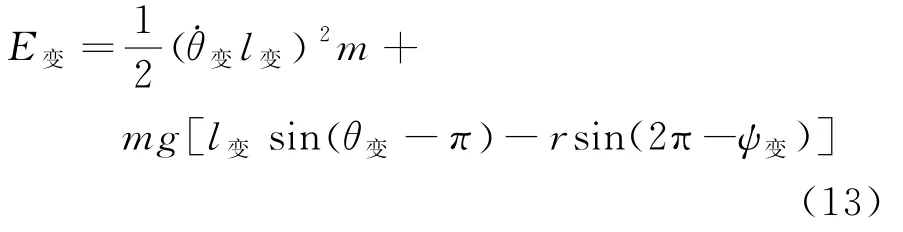
最高处的机械能可表示为

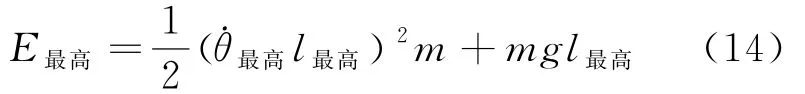
因为临界时刻之后m能量守恒,因此E最高=E变,而且m在运动过程中任意时刻都有θ,联立式(13)、式(14)可得

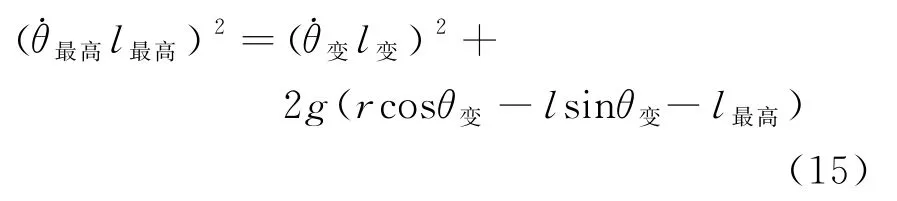
m在最高点处沿eτ(此时eτ方向为竖直向下与g同向)方向的加速度为

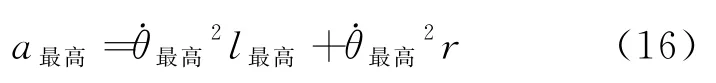
式(16)右边第一项为速度方向改变所产生的加速度,第二项为速度大小改变所产生的加速度。要想能越过最高点,只有满足式(17),才能保证越过最高点时绳中有张力。根据绳不可伸长可得

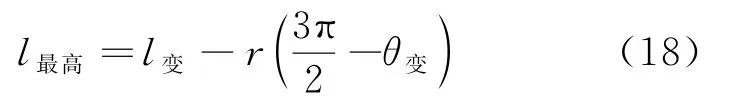
联立式式(15)、式(16)、式(17)、式(18)得

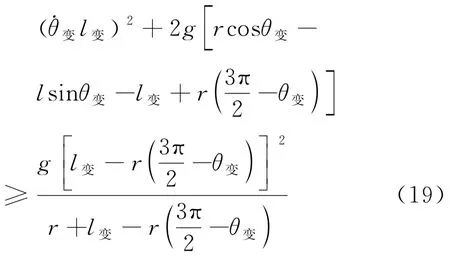
当满足式(19)时,m在最高点时绳能绷紧,意味着m可以越过最高点,也就是能形成循环摆。不等式中r,g为常数,根据θ变,l变可判定不等式是否成立,而θ变,l变,可通过求解定初值的微分方程来确定。结合1.1.3节中的微分方程和式(19),便可通过初值判断能否形成循环摆。

2 数值求解

因为m做循环摆运动的速度极快,整个过程通常小于1秒,实验准确记录困难。笔者曾尝试用相机直接记录m轨迹,再与理论值对比,发现误差较大。进而调整策略,选择验证不同初始条件下的临界时刻的各物理量实验值是否与(数值求解得出的)理论值相符合的方案。

将θ,lvM的实验值与理论得到的数值解对比分析,可验证理论分析中的假设是否合理、理论模型是否正确,进而可验证形成循环摆判定条件式(19)是否正确。

由于变量较多,所以可以先在其他条件不变的情况下,研究某一个参量对循环摆的影响。我们对各变量赋值如下14,杆半径r=0.0042m,摩擦系数μ=0.2,初始角度θ0=0,初始线长l0=1m,通过控制单一变量的方法,逐一探究该变量对循环摆的影响。

3 实验验证

3.1 实验方案

根据理论分析,可知影响体系的变量主要有5个,分别为杆半径r,摩擦系数μ,质量比,初始角度θ0,初始线长l0。因涉及到变量较多,所以笔者采用控制单一变量法,研究某一变量对体系的影响。但在研究过程中发现即便是材质相同的杆与线,由于表面光滑程度不一样也会导致摩擦系数不一样,而在改变杆半径r时,势必要更换杆,因此会导致摩擦系数μ也发生改变,无法达到控制单一变量的要求,从而无法得出正确的结论。因此,在本实验中不改变杆半径和摩擦系数,所采用的杆与细线的摩擦系数为0.2086±0.0022,半径为(0.420±0.003)cm 的钢杆,在改变某一参数时,其余的参数为l0=(1.0000±0.0004)m,θ0=(0.00±0.04)rad=14.000±0.002。在其他条件相同时,分别设计不同θ0,l0的数值,先用视频记录,后使用Tracker分析实验视频,最后用Origin分析处理实验数据,并与理论模拟所得曲线进行比较。

3.2 实验装置

图6为我们采用的实验装置,由于摩擦系数μ与杆半径r在图中比例太小,难以标出,其余的各个物理量已经在图中标出。

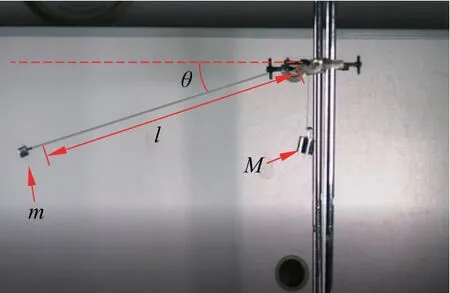
图6 实验装置

3.3 利用临界时刻的各个物理量验证微分方程组

我们采用如下方法从视频中分辨出临界时刻。因为,仅仅看m的运动轨迹是无法分辨的。可是分析M运动,不难发现,在临界时刻时,vM为0(vM=0后m便做渐开线运动,也就是说虽然初始时刻时也有vM=0,但不满足=0,因此舍去t=0),因此M速度为零时的各物理量便是临界时刻的各个物理量。显然M仅做直线运动,而且速度相对于m较缓慢,既容易从视频中确定M速度为零的时刻,而且误差又小。比对临界时刻各个物理量的实验值与理论值,以此来验证本文的理论是否正确。

图7中实线均由理论值得出(下同,略)。图中所标的极限角度、极限线长、极限角速度、极限时间的意义分别为θ变、l变、t变。

从图7中可以看到,理论值与实验值符合的较好。证明微分方程模型与实际情况较为贴合,在推导微分方程组时做作的假设合理。

为了进一步对图7中的各图进行对比分析、归纳总结,

首先要明确θ变、l变、t变反映了体系的何种性质,以及、l0、θ0对系统的影响:

(1)θ变和l变,表征临界时刻m的位置信息。

(2)t变,间接表征系统整体运动快慢:t变越小,循环摆的时间越短,运动越快。

(7)θ0间接表征了体系的初始能量,在其他条件不变的情况下,θ0越小,体系总能量越大。

其次,从图7中各图变化趋势来看:发现图7中(a)、(b)、(c)显示:θ变与、l0、θ0呈正相关。

对比图7中(d)与(g)、(e)与(h)、(f)与(i),发现两两变化趋势均相反。而且经过理论计算和实验验证,(f)与(i)的极值点相同(l变与在相同的θ0下取到极值),此结果表明,改变、l0、θ0中的任一个,l变与的变化趋势总是相反。而两者乘积在表征了在临界时刻m单位质量的角动量的大小,又因为两者变化趋势相反,可知,不同条件下的临界时刻m的角动量应该相差不大。基于上述分析,我们可以得到以下结论:

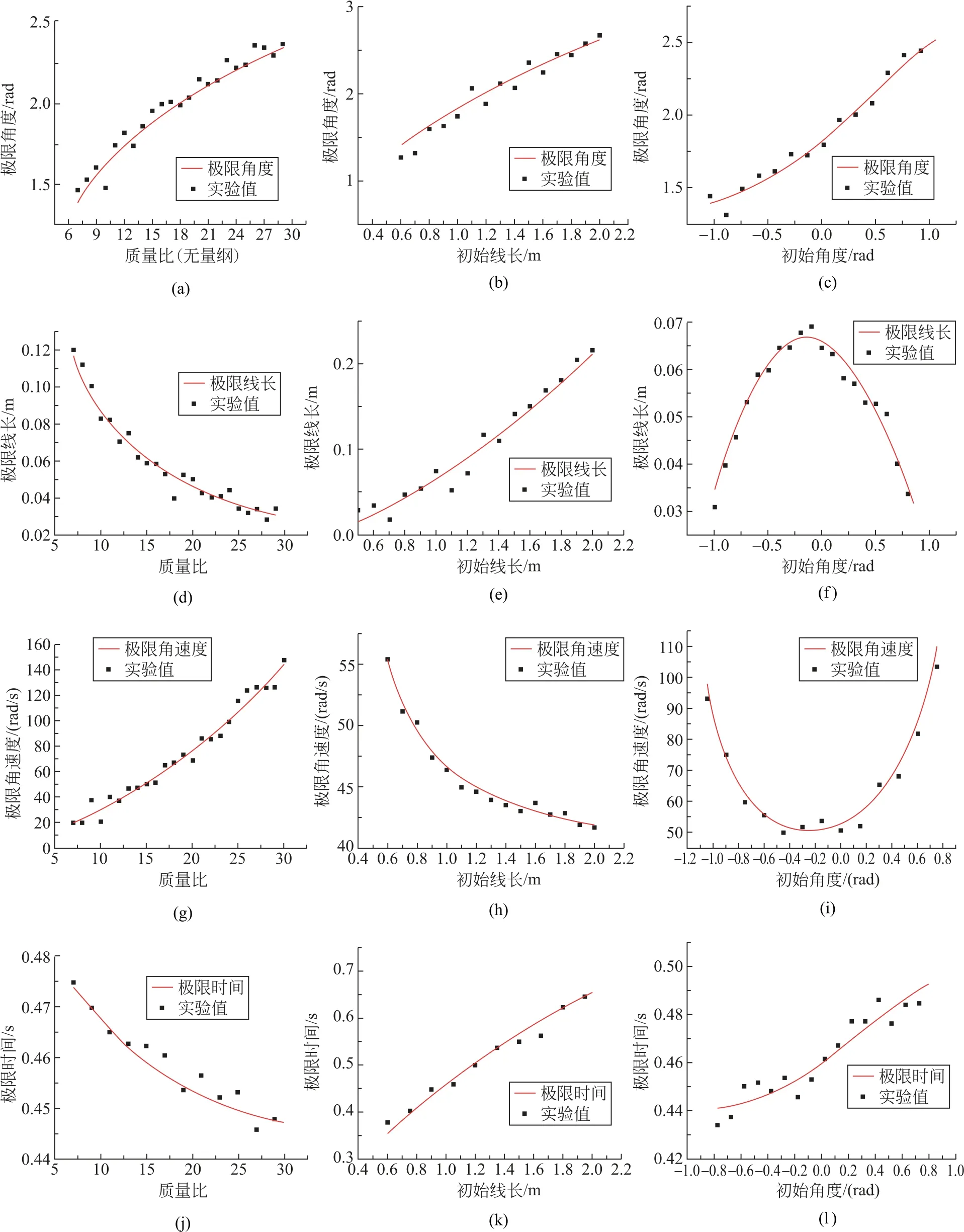
图7 初始条件对临界时刻物理量的影响

有了上述分析后,接下来分析12幅图的变化所代表的物理规律:

其次,分析图7中(b)、(e)、(h)、(k)。根据3.3节(6)的分析,随着l0增大,体系运动应该是减缓的,相比较上一段所分析的令体系运动加快,图7中(b)、(e)、(h)、(k)与图(a)、(d)、(g)、(j)的变化趋势本应全部相反,事实上图(b)并不符合此规律。图(b)中θ变与l0呈正相关,缘于改变l0时t变的增加速度比˙θ的减小速度要快。所以,t变对θ变的影响比l0对θ变的影响更大。

最后,分析图7中(c)、(f)、(i)、(l)。图7(l)表明t变与θ0呈正相关关系,因为θ0越大,体系总能量越小,体系运动越慢,t变变长。理论计算显示:图(f),(i)中存在一阶导数为零的点,图(c)中存在二阶导数为零的点,且上述所有阶导数为0的点在同一个θ0下取到。

图7中(f)、(i)这两图表明l变和与θ0并不是简单的正、负相关关系。这是因为当θ0较小时,m相对位置较高,体系能量较大,因而体系运动相对较快,导致l变较小较大;而当θ0较大时,体系能量较低,导致体系运动较慢,所以t变比较大,因此也导致l变比较小。综上所述,l变存在一个极大值。而与l变的变化趋势相反,因而存在一个极小值。

图(c)中θ变,在二阶导数为零的点之前,随着θ0增大减小且t变增大,所以在此阶段θ变对θ0的变化率越来越大,而在二阶导数为零的点之后随着θ0增大也随之增大,因此θ变对θ0的变化率越来越小。

3.4 通过实验验证循环摆判据的正确性

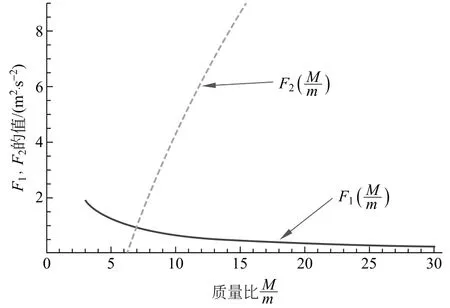
图8 不同质量比下F1,F2的变化

3.4.1 用验证循环摆的判据

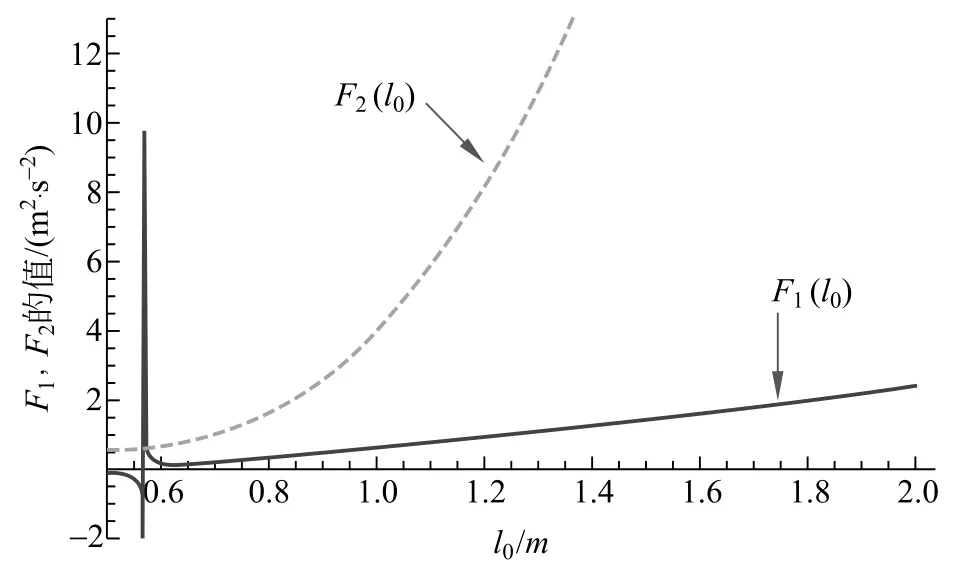
图9 不同l0下F1,F2的变化

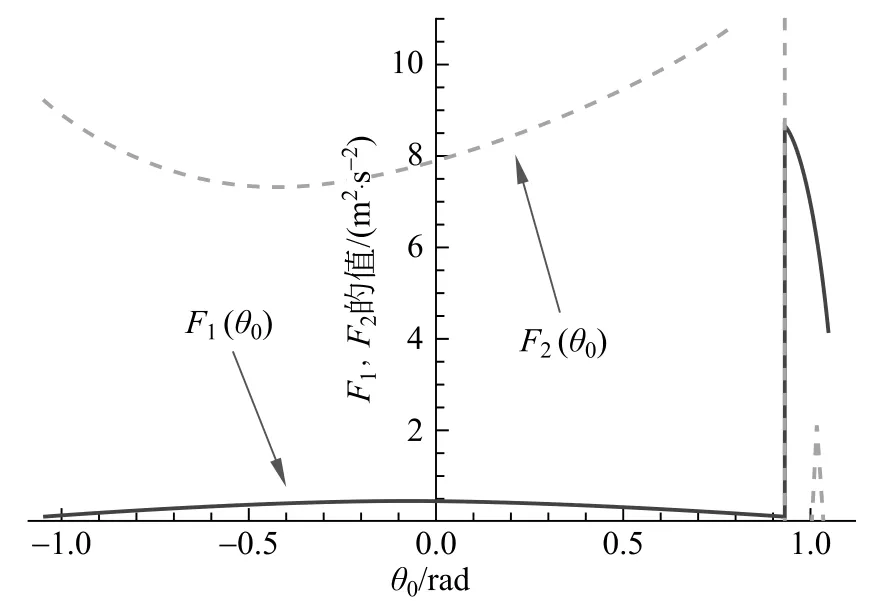
图10 不同θ0下F1,F2的变化

首先改变质量比,通过Mathematical作图得到图8,根据图8 可以得到,只有当质量比大于6.992时,才满足F1＜F2。

而在实验中,在其他条件不变的情况下,取质量比为6.000±0.002,无法形成循环摆。而质量比为7.000±0.002时,刚好能形成循环摆,与理论相符合。

3.4.2 用l0 验证循环摆的判据

看到图9中在l0=0.56处F1存在突变,当l0＞0.561m 时,有F1＜F2,这意味着当l0＜0.561m时,无法形成循环摆。

在实验中观察到当l0=0.5000±0.0004m时,m未绕杆一圈便会与杆碰撞,此现象正是图9中突变的原因,因为当撞击时m的运动规律就不能用1.1.3节中的微分方程组描述,因此方程的数值解在那一点会发散,反应到图上就是突变。l0过小,在临界时刻前便会与杆碰撞。当l0=(0.6000±0.0004)m 时,在与杆相撞之前,m恰好能到达最高点附近。实验与理论符合较好。

3.4.3 用θ0 验证循环摆的判据

看到图10 中在θ0=0.92 处F1,F2存在突变,且θ0＜0.92 时,有F1＜F2,意味着当θ0＞0.92≈0.3π便无法形成循环摆。

实验中测得,当θ0=(0.79±0.04)rad能明显形成循环摆现象,而当θ0=(1.05±0.04)rad时,不能形成循环摆。在此条件下,当m运动到大于1.2π时,无法使绳子绷直,此后做斜抛运动下落。因此,这一点之后的时刻便不能用1.1.3节中的微分方程组描述,数值解在这一点发散,体现到图中便是突变,图10与理论相符合。