基于可靠度的输电塔维修决策研究

曾德森，王松涛，夏 谦

（1.电力规划设计总院，北京100120；2.中国电力工程顾问集团中南电力设计院有限公司，湖北 武汉430071）

0 引言

输电杆塔是重要生命线工程之一的电力系统的重要组成部分，对输电线路的良好运行起着举足轻重的作用。但是输电杆塔属于对风荷载作用敏感的高耸结构，组成杆塔的构件在服役期内长期处于风力作用下难免产生疲劳损伤，导致杆塔结构的性能退化，抵抗极端环境作用的能力降低以致最后发生事故。如何避免结构因疲劳损伤累积造成事故，是值得探索和研究的课题之一。

曾超和奚绍中［1］根据Virkler 的试验结果，结合中心极限定理，推导出钢构件的疲劳寿命概率分布函数以及考虑了初始缺陷的构件疲劳可靠度函数；李臻［2］介绍了疲劳裂纹起始寿命起主导作用时试件的变幅疲劳寿命估算方法，并通过实验验证该方法的准确性；在输电杆塔维修决策方面，韩富春等［3］针对运行20年以上的输电杆塔的运行状态提出了良好状态、注意状态和不良状态的具体标准。国内外学者研究主要集中在构件的疲劳可靠性分析层面，针对结构系统的疲劳可靠性分析方面的文献较少。

基于此，本文对既有输电杆塔的维修决策进行研究，旨在建立一套基于疲劳可靠度的输电杆塔的预防维修决策方法，实现维修时机的预测，以保证结构的疲劳可靠性，同时考虑维修的经济相关性，优化维修计划降低维修成本，以避免结构因疲劳损伤累积造成的重大事故。

1 重要构件选择两步法

通过大型有限元软件ANSYS 建立输电杆塔结构模型，施加等效风荷载计算，根据各构件的应力挑选出必须监测的构件和建议监测的构件；运用灵敏度分析，考察各构件变化对一阶振型的影响确定出构件的相对重要性，实现必须监测构件全监测、建议监测构件按相对重要性选择性监测的目的。

1.1 输电杆塔的有限元模型

本文以某输电杆塔为原型，利用大型有限元软件ANSYS 建立了有限元模型，该塔总高度为108 m。采用BEAM188梁单元来模拟输电杆塔的构件，材料特性简化为线弹性材料，弹性模量为2.06 GPa，泊松比0.3，不考虑基础预埋部分，将支座视为固定支座。

图1 有限元模型图Fig.1 Finite element model

图2 塔体节段模型Fig.2 Tower body segment model

1.2 等效风荷载下应力分析

1.2.1 等效风荷载计算

在进行输电杆塔的应力分析之前，需要进行风荷载的计算。风荷载可以分解为平均风和脉动风，平均风的大小和方向基本不随时间变化，相当于静力荷载，其作用在输电杆塔上的响应仅与杆塔的刚度和风荷载的大小有关；而脉动风会随时间随机变化，相当于随机动力荷载，其作用在输电杆塔上会引起结构的振动，是一个与杆塔的刚度、动力荷载、质量和阻尼等相关的随机变化量。在工程实际应用中，可以按照杆塔响应最大值一致的原则将脉动风荷载等效为静力荷载，将脉动风荷载对杆塔的动态作用转化为简单的准静态作用。

输电杆塔高度z处的等效风压设计值和风荷载可表示为：

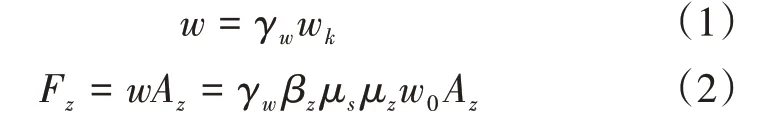
式（1）、式（2）中，γw为风荷载分项系数，取1.4；Az表示高度z处垂直于风向的挡风面积；w0为基本风压；μz为风压高度变化系数；μs为风荷载体型系数；βz为输电杆塔风振系数。

1.2.2 输电杆塔的应力分析

在90°大风工况下，将1.2.1 节中确定的等效风荷载施加在输电杆塔上，可以分析出各构件的应力。

从应力图图3 中可以看出，本文工况下最不利受力杆件为对角上的主要承受压力和主要承受拉力的塔身主材，其在整个杆塔高度范围内都具有较大的应力，尤其是在五六节段的变坡度处，压杆和拉杆的应力很大，因此建议将整个高度范围内的杆塔塔身主材作为必须监测的构件。

除了塔身主材外，从应力图中还可以看到六段以上（含）的连接塔身主材的斜材、横担上下弦杆和各段连接塔身主材的水平杆件具有较大的应力，作为建议监测的构件。基于应力的构件重要性分析只能定性地判断哪些构件受力大，是必须监测的构件。但是除塔身主材外，其余构件的应力水平相差并不是很大，需要进一步对这些构件的重要性进行分析，以便当技术经济条件不允许对这么多数量的构件同时监测时，能将有限的资源用在重要性级别较高的构件上。

1.3 基于灵敏度分析的构件重要性分析

1.3.1 结构的灵敏度分析

从灵敏度在动特性修改领域的应用来看，灵敏度分析可以较好地估计待修改的参数对结构特性的影响，因此本文利用灵敏度分析来确定出构件的重要性。

图3 各段应力图Fig.3 Stress diagram of each section

考虑一个离散线性系统的固有振动问题，若不考虑结构阻尼，则该n 自由度离散系统的固有振动方程可以表示为：

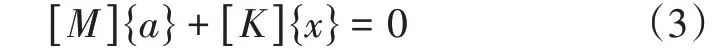
式（3）中，［M］、［K］分别为离散系统的质量和刚度矩阵，为实对称的n×n阶矩阵；{a}、{x}分别为离散系统的加速度和位移响应，为n× 1的列向量。

上述的振动方程的求解可以转化为求广义特征值的问题，有：

式（4）中，λi为第i个本征值，等于系统第i阶固有频率ωi的平方。φi为第i个本征向量，由于各本征向量之间是线性独立的，因此亦可将其看成n维空间的一个正交基，作为该离散系统的第i阶模态。

若系统中各构件的设计参数为pm，根据矩阵求导的基本理论，对式（4）进行求导，可得：

2）各阶振型对设计参数的一阶灵敏度分析

根据Fox［4］提出的可以将特征向量导数表达为截尾模态组的线性组合的理论，第i阶振型关于设计参数的一阶灵敏度可以表示为：

式（8）中，αr表示第r个本征向量的组合系数，φr为第r个本征向量。

若对式（5）左乘{φj}T，将式（8）代入，式（8）中的线性组合系数取值如下：

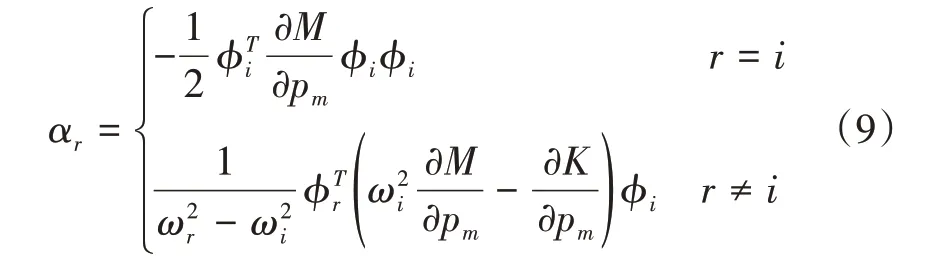
在进行灵敏度分析时，由于实际工程中构件的损伤主要表现为构件的刚度降低，而作为单元刚度矩阵组成部分的弹性模量可以反映构件的刚度变化，因此本文取构件的弹性模量E作为设计参数。将第m个构件的弹性模量设为Em，代入式（6）、式（7）、式（8）得到系统模态参数对构件弹性模量的灵敏度方程，如式（10）所示。

1.3.2 输电杆塔的灵敏度分析

考虑到输电杆塔具有顺风向和横风向两个振动方向，故对两个方向计算出来的归一化灵敏度值进行加权平均计算以综合考虑两个振动方向的灵敏度指标，进而挑选出全局意义上的重要构件，本文将顺风向和横风向两个振动方向的权重均设为0.5。对该有限元模型进行灵敏度分析时，首先提取出各构件的单元刚度矩阵、塔架结构各阶平动模态的频率和振型，再代入式（10）计算一阶振型顶部节点值对构件弹性模量的灵敏度。本文模态顶点取第88号节点，该节点位于输电杆塔主塔杆的顶端。输电杆塔前三阶平动模态的固有频率如表1 所示，输电杆塔X、Y 方向前三阶平动模态的振型图如图4所示。

表1 各阶模态的固有频率（单位：Hz）Table 1 Natural frequency of each mode(Unit:Hz)

图4 输电杆塔X、Y方向前三阶平动模态振型Fig.4 The first three translational modes of transmission towers in X and Y directions

X、Y 方向一阶模态固有频率和模态振型第88 节点处对各构件弹性模量变化的归一化灵敏度值，如图5 和图6 所示。综合考虑X、Y 两方向的加权平均归一化灵敏度值，如图7 所示。各构件弹性模量的变化对振型顶部节点值的影响是不同的，且相差很大，通过对比有限元模型图可以看出影响较大的构件主要是输电杆塔的塔身主材和连接塔身主材的斜杆、横担上下弦杆，与基于等效静风荷载分析的结果是一致的，验证了提出的基于灵敏度方法的重要构件选取是有效的。

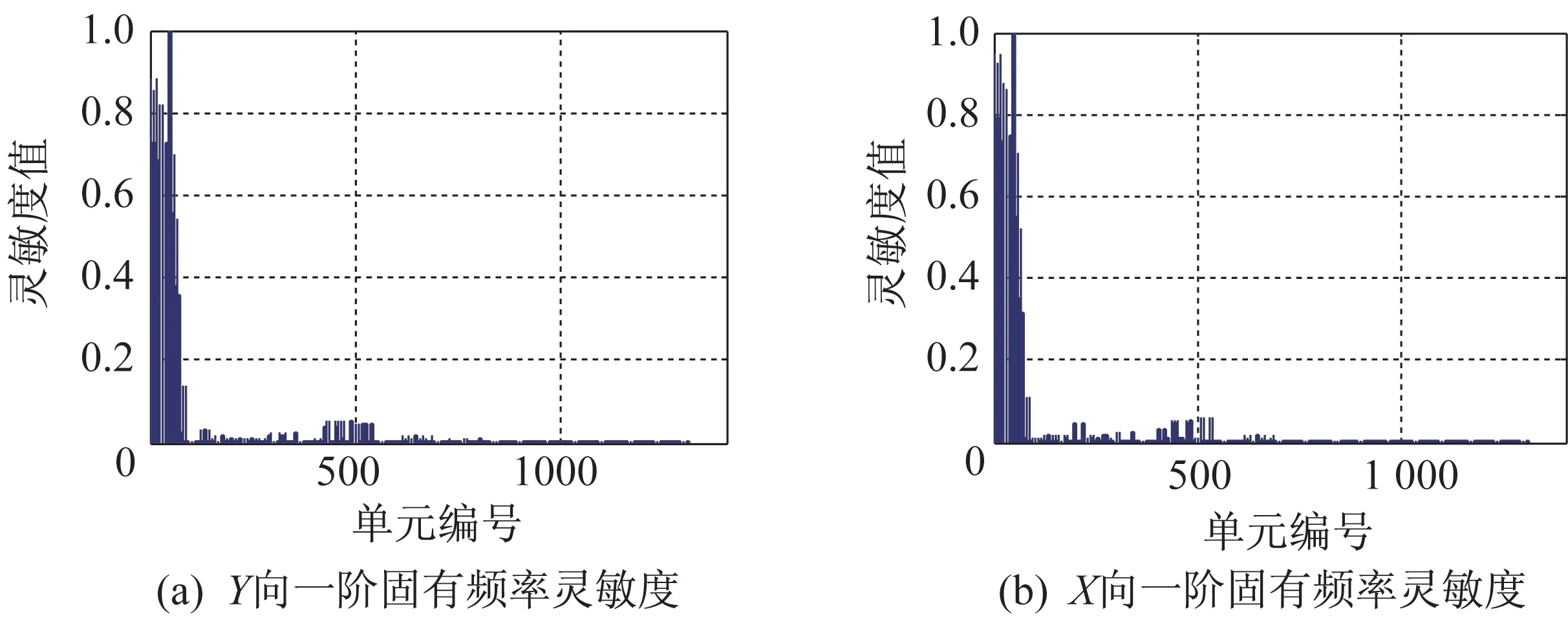
图5 输电杆塔X、Y方向第一阶固有频率对构件弹性模量的灵敏度Fig.5 Sensitivity of first-order natural frequencies in X and Y directions of transmission towers to elastic modulus of components

图6 输电杆塔X、Y方向第一阶振型第88节点处对构件弹性模量的灵敏度Fig.6 Sensitivity to the elastic modulus of members at the 88th node of the first mode shape in the X and Y directions of the transmission tower

图7 综合考虑X、Y两方向的一阶振型顶部节点加权平均归一化灵敏度值Fig.7 Comprehensive consideration of the weighted average normalized sensitivity value of the top node of the first-order mode in the X and Y directions

只要确定出构件材料的P-S-N 曲线三参数幂函数估计式中的各参数和构件的变异系数，即可利用式（11）计算出构件在应力幅为S条件下的疲劳失效函数和可靠度函数。

张春涛［6］博士对材料的疲劳性能进行了系统研究，根据重庆地区降雨情况建立了酸雨腐蚀模型，考察Q345 钢材随酸雨PH 值、腐蚀方式和腐蚀时间的不同所出现的腐蚀现象及材料性能的退化规律，建立相应的P-S-N曲面模型。

2 重要构件的维修决策

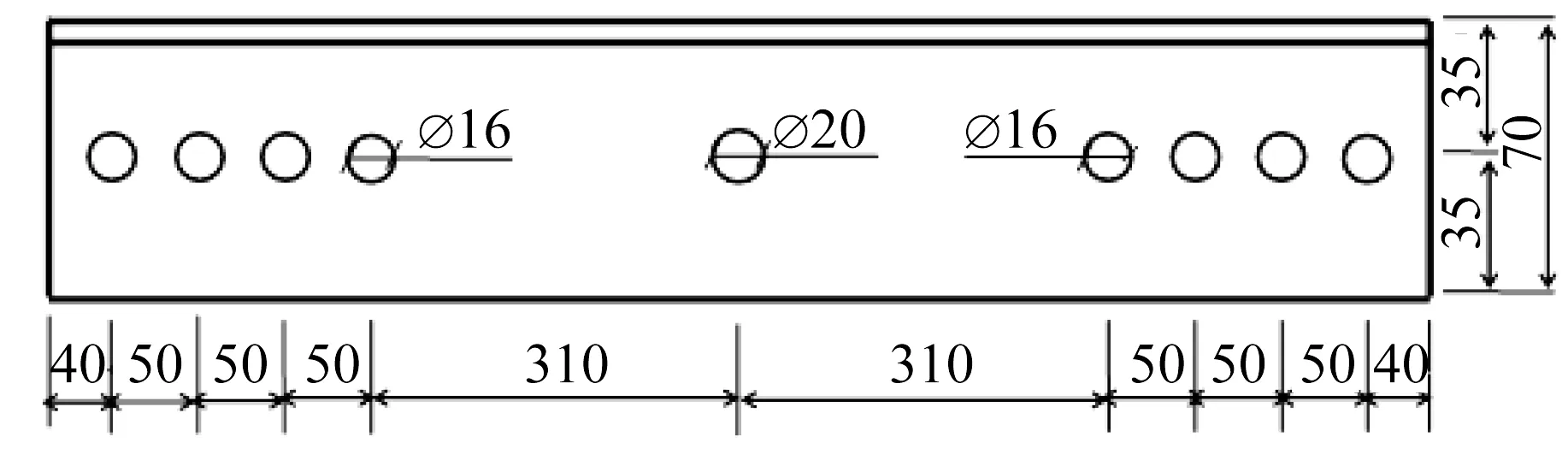
图8 试件几何尺寸Fig.8 Geometric size of test member

2.1 疲劳失效函数和可靠度函数的确定

根据文献［5］给定应力脉S后构件的疲劳失效函数和疲劳寿命可靠度函数为

从表2 中数据可以看出：1）构件的疲劳寿命随疲劳振动荷载Smax的增大而减小；2）间隔疲劳振动条件下构件的疲劳寿命明显比连续疲劳振动条件下的疲劳寿命长，且疲劳振动荷载较大时疲劳寿命延长比例较高。

由上述试验结果，并考虑单点小子样试验的离散性，可以得到考虑可靠度置信水平的γ-P-S-N曲线表达式参数［7］，如表3所示。

表2 疲劳寿命试验结果Table 2 Fatigue life test results

表3 不同置信水平和不同可靠度的纯疲劳S-N曲线参数Table 3 Pure fatigue S-N curve parameters with different confidence levels and different reliability

为了使用方便，本文计算疲劳失效函数和可靠度函数时采用γ= 95%，P = 50%情况下的S-N表达式，

2.2 重要构件的维修决策

2.2.1 重要构件维修时机决策模型

假定构件正常工作时要求其疲劳可靠度不小于R0，即疲劳可靠度阈值为R0，由式（11）有

图9 R-N曲线Fig.9 R-N curve

图10 故障率演化模型Fig.10 Failure rate evolution model

图9反映了构件的疲劳可靠度与疲劳寿命之间的关系，横坐标为构件的疲劳寿命N，纵坐标为构件的疲劳可靠度R。可以看出，当构件的疲劳可靠度小于R0或构件已经运行的时间超过Nr时，需要采取措施对构件进行维修［8-9］。

2.2.2 重要构件维修方案决策

为保证输电杆塔结构在设计基准期内的疲劳可靠度始终处于可接受的范围，对重要构件实行疲劳可靠度满足一定疲劳可靠度阈值的不完全维修。鉴于组成输电杆塔的各构件随着杆塔运行时间的延长其维修频率会增大的事实，采用改进因子法建立重要构件的不完全维修模型。文献［10-12］故障率的演化模型如图10所示。

混合模型中每次预防性维修前后构件的失效概率函数有如下的关系［13-14］：

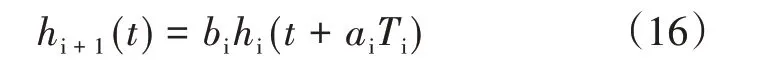
式（16）中，ai为役龄回退因子，其值处于0 和1 之间；bi为故障率递增因子，其值大于1，ai和bi要根据历史维修数据得到；h1（t）为构件刚刚投入使用时的失效概率函数，i为预防性不完全维修的周期数，相应的hi（t）和hi+1（t）分别为构件的第i次和第（i+1）次预防性维修；Ti为两次维修之间的维修间隔。

3 算例分析

以1.3.2节中建立的输电杆塔结构为研究对象，选取4根杆件为例进行基于疲劳可靠度的输电杆塔预防性维修决策。首先本文进行如下几个假定：

1）构件的疲劳寿命概率密度函数服从威布尔分布［15-17］，P-S-N曲线服从三参数幂函数，曲线中参数采用3.2.2 中的取值。构件均采用Q345 级钢材，可靠度置信水平均取0.95，P-S-N 曲线中各参数P、m、m'、S0、Cp'统一取为0.5、4.40、-0.049、65.531、3.552e13。

2）构件在进行监测前，即建立预防性维修决策系统之前已经存在损伤，损伤量由检测结果确定。

3）输电塔架各构件所处环境差异不大，假设各构件的役龄回退因子和故障率递增因子相同［18-20］。选取的4根构件的分析参数如表4所示。

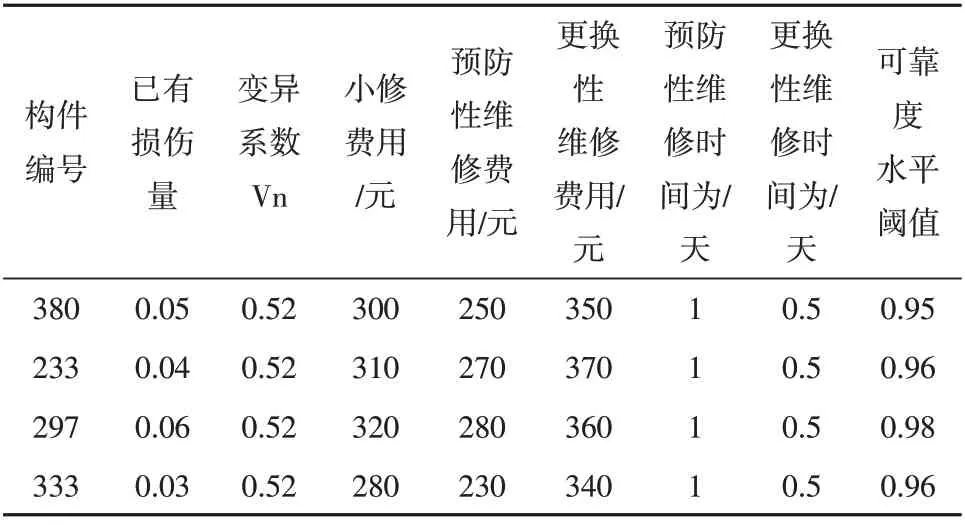
表4 各构件的分析参数Table 4 Analysis parameters of each component

根据以上参数结合编制基于疲劳可靠度的输电杆塔预防性维修决策计算程序，设定机会维修阈值为0，可以计算出不考虑机会维修情况的总维修费用为35 674元。采用基于机会维修的成组维修方法进行优化，将机会维修阈值设为3 a，增量为0.25 a，计算结果如表4 所示。从表中可以看出，基于机会维修的成组维修方法最小的总维修费为28 457 元，成本节约了20.23%，表明该方法是有效的。表5 列出了当机会维修阈值取3 a时的维修计划，表中的0、1、2分别表示不进行维修、进行预防性维修和进行更换性维修，如在第80.09年，应当对380号构件进行更换、对233号构件进行预防性维修，297号和333号构件不进行维修。可见基于机会维修的成组维修方法可以实现输电杆塔服役期内的多构件预防性维修决策，实现保证输电塔架结构的可靠性和维修费用最低。

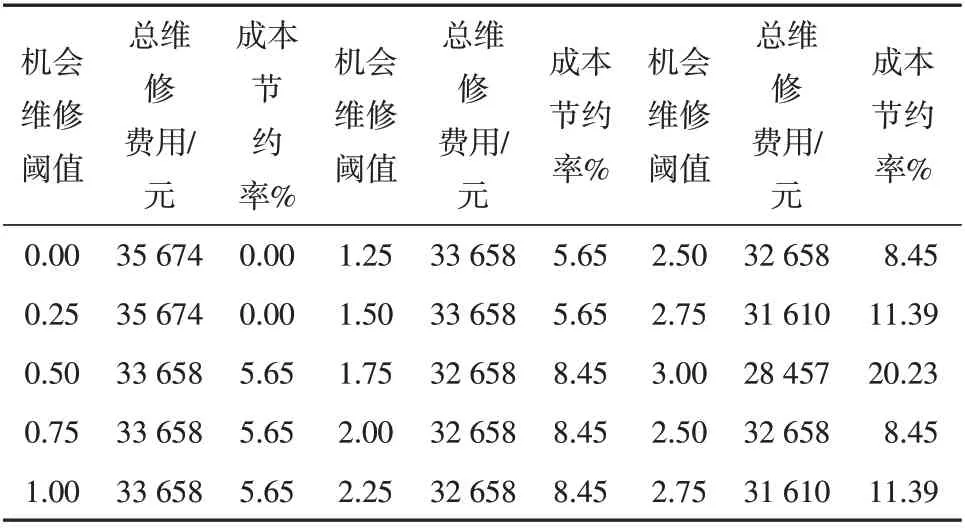
表5 基于机会维修的成组维修方法计算结果Table 5 Calculation results of group maintenance method based on opportunistic maintenance

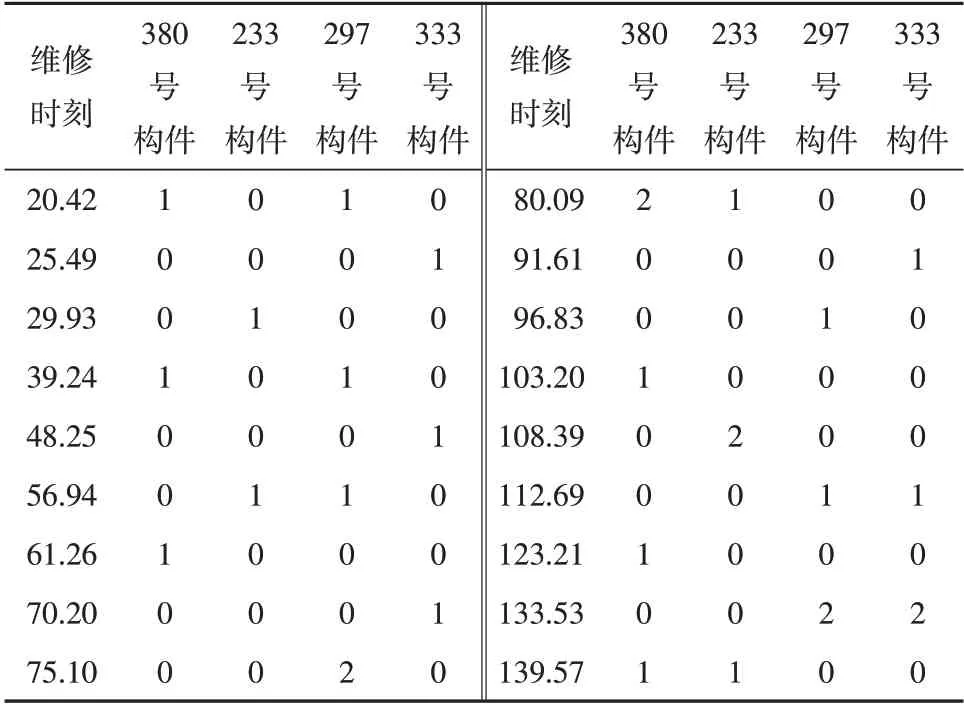
表6 最优维修计划表Table 6 Optimal Maintenance Schedule

4 结语

本文提出了一种基于等效风荷载作用下应力分析和灵敏度分析的重要构件确定两步法，即利用大型有限元软件ANSYS建立输电杆塔结构模型，对其施加等效风荷载，根据构件的应力水平确定为必须监测构件以及建议监测构件；在此基础上运用灵敏度分析，按照构件变化对杆塔一阶振型的影响程度确定构件的相对重要性，从而实现了必须监测构件全监测、建议监测构件按相对重要性选择性监测的目的，则在实际工程中可根据经济条件和实际需要合理地确定重要构件。

在构件层次实现了维修决策，假定构件的疲劳寿命服从威布尔分布，基于试验获得的P-S-N 曲线推导了构件的疲劳可靠度函数。杆塔的重要构件应力幅大、疲劳寿命相对较短，一旦发生疲劳失效后果严重，对这类构件建立了预防性不完全维修决策模型，在保证构件疲劳可靠度的基础上以单位时间内维修成本最小为目标确定了重要构件的维修方案。

针对输电杆塔结构体系建立了基于机会成组维修的预防性维修决策模型，在保证构件可靠度的要求下，以杆塔服役期内总维修费用最小为目的，通过调整机会维修阈值，制定了最优维修计划。