聚焦操作思辨 理解概念本质——《分数的初步认识（二）》教学实践与思考

文|林小平

《分数的初步认识（二）》是苏教版三年级下册第七单元第一课时的教学内容。学生在三年级上册已经认识了一个物体或一个图形的几分之一和几分之几，认识一个整体的几分之一是对分数含义的进一步丰富，同时为今后抽象出分数的意义、理解分数的性质奠定基础。对于学生来说，理解一个物体的几分之一比较容易，但理解一个整体的几分之一却有一定难度。这是因为把一个整体平均分之后，分数表示的仅仅是部分与整体的关系，其表达形式与一份的实际数量完全不同，学生原有的认知经验会对其用分数表示平均分的结果造成干扰。

如何实现认知的突围和生长？瑞士心理学家皮亚杰的认知发展理论中有两个重要的概念：同化和顺应。学生学习一个物体的几分之一，是概念同化的过程，而学习一个整体的几分之一，则要经历概念顺应的过程。本次教学，笔者设计了丰富的操作与思辨活动，让学生经历同化、顺应的过程，从而对分数概念的理解逐步加深，对数学思考的表达拾级而上，顺利实现从具体到抽象的意义建构，为将来进一步抽象分数的意义提供有力的支持。

一、复习一个物体的二分之一

师：瞧，两只小猴正在玩耍，孙小圣来了，带来了它们最爱吃的桃。把一个桃平均分给2 只小猴，每只小猴分得这个桃的几分之几？

生：把一个桃平均分给2 只小猴，就是把一个桃平均分成2份，每只小猴分得这个桃的

师：在以前的学习中我们知道，把一个物体平均分成2 份，每份是它的

【思考：创设“把一个桃平均分给2 只小猴”的问题情境，能唤醒学生对原有分数的认识，激活已有活动经验，为接下来学习一个整体的二分之一做好铺垫。】

二、认识一个整体的二分之一

师：吃完了这个桃，两只小猴直呼不过瘾，于是孙小圣又拿来了一盘桃（课件出示一盘盖好的桃）。想一想，如果把一盘桃平均分给2 只小猴，每只小猴分得这盘桃的几分之几？

生：因为把一盘桃平均分给2只小猴，每只小猴分得这盘桃的一半，一半就是它的

师：很有想法！现在《学习单》上就有一盘桃，请你先数一数，再分一分，然后涂一涂，表示出你的这盘桃的

学生在《学习单》上操作后，实物投影展示并交流。

课件呈现：

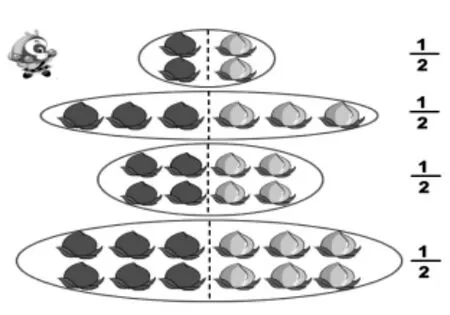
师：这四个同学在分桃的时候，有什么相同的地方？又有什么不同的地方？

生：相同之处都是将盘子里的桃平均分成2 份，每一份都是这盘桃的不同的是每盘桃的表示的实际个数不同。

师：每盘桃的总数不同，每一份的个数也不同，为什么都可以用表示？

生：我们发现，不管一盘桃有几个，都可以把这盘桃看作一个整体，只要平均分成2 份，那么每份都是这盘桃的

师：同学们真厉害，从这么多的“不同”中找到了“相同”的地方。继续思考，你还能把多少桃看作一个整体？

学生举例：20 个桃、99 个桃、一篮桃、一筐桃……

【思考：本环节承上启下抛出操作任务：表示出你的这盘桃的二分之一。因为每个人的一盘桃虽有具体个数，但个数又不尽相同，所以操作具有挑战性，结果又兼具个性化。学生经历独立操作、合作交流、同中求异、异中求同、抽象与不完全归纳等探究活动，深刻理解了“一个整体的二分之一”的含义，凸显了分数的本质。】

三、认识一个整体的三分之一

师：小猴欢欢、乐乐和圆圆在用分数表示涂色部分，谁的表示是正确的？

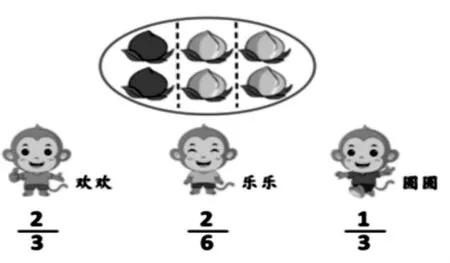
生：把6 个桃看作一个整体，平均分成3 份，涂色部分是这个整体的

师：欢欢和乐乐的错误是受到了什么的影响？你想提醒同学们注意什么？

生：不受个数的影响，重点看清平均分成几份，涂了几份。

【思考：在“三只小猴学分数”的问题情境中，以辨析题的形式引领学生认识“一个整体的三分之一”。这样设计，既突出重点，又寓教于乐，通过质疑、反思、提醒等教学活动，使得分数的本质更加凸显，学生的理解更加深刻。】

四、认识一个整体的几分之一

师：想知道孙小圣送来的这盘桃到底有多少个吗？（出示“试一试”）看，这12 个桃除了可以平均分成2 份，得到它的二分之一，还能平均分成几份，得到它的几分之一呢？先分一分、填一填，再和同学交流。看看你能找到几个分数？

学生在《学习单》上操作后，实物投影展示交流。

师：都是分12 个桃，每一份为什么用不同的分数表示？

生：因为平均分的份数不一样。

生：把一个整体平均分成几份，每份就是它的几分之一。

师：同学们真了不起！从“相同”中又找到了“不同”。

【思考：引导学生通过操作和思辨，自主认识“一个整体的几分之一”。这样设计，便于学生由特殊推及一般，比较时侧重同中求异，突出平均分的份数不同，表示每份与整体的关系的分数也不同，发展学生的数学思考。】

五、回顾总结，内化新知

师：今天我们再次认识了几分之一，和以前的几分之一比较，你有什么新的认识？

生：前后比较，平均分的对象发生了变化。以前都是把一个物体平均分，现在是把一些物体组成的一个整体平均分。

生：不管是分一个物体，还是分一个整体，几分之一表示的都是总份数与每一份之间的关系。

【思考：通过对新知与旧知的深刻比较，丰富了分数的内涵，凸显几分之一内在本质的一致性，即分数表示部分与整体相互依存的数量关系。同时，对数学知识和方法的溯源反思，能帮助学生有效建构知识结构，对学生数学综合素养的提升大有裨益。】

六、综合应用，拓展提升

1.看图写分数。

师：接下来，我们跟着孙小圣去寻找更多的分数。首先来到果园，一起来解决果园里的数学问题吧！请你用分数表示涂色部分。

学生先在《学习单》上填一填，再集体交流。

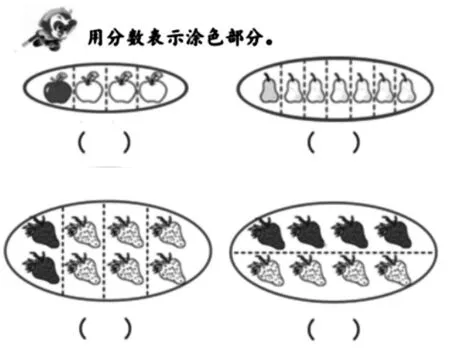
师：观察图三和图四，每个整体都有8 个草莓，为什么图三用表示，图四用表示？

生：虽然一个整体包含的个数相同，但是平均分的份数不同，每一份表示的分数也不相同。

2.“想想做做”第3 题。

师：出了果园，来到农场。农场里也有数学问题。请你在每个图里分一分，并涂色表示它右边的分数（图略）。

学生独立涂色，集体交流时先说说分数的含义，再说说分、涂的方法。

3.变式拓展题。

师：最后，我们跟着孙小圣来到了花果山。小猴们出了道题想考考大家，愿意接受挑战吗？一起来听！（播放录音：我俩占我家小猴总数的，你知道我家有多少只小猴吗？）

师：看，18 只小猴出来欢迎大家了。除了能找到18 只的是2只。你还能找到它的几分之一是几只？在找的过程中，你还发现了什么?

生：同样一个整体，由于平均分的份数不同，就能得到不同的分数。

4.趣味思考题。

师：同学们的表现太出色了，老师想给大家一些奖励。看，这是智慧星。

生：因为一个整体的个数在发生变化，所以每次拿走的颗数就不一样。

师：（小结）总数发生了变化，每份的个数也会发生变化。分数真是太神奇了！今后我们还会继续研究这种神奇的数。

【思考：基于对一个整体的几分之一的理解和应用，用有趣的故事情境串联起习题，通过深度挖掘和加工，使得习题既突出针对性和层次性，又强调挑战性和趣味性。让学生深刻理解“一个整体”概念的丰富性，初步体会分数之间内在的关系以及关联性，感悟分数的本质意义和价值。】