发动机喷流对飞机阻力伞性能的影响
2021-05-06冯传奇孙建红喻东明许常悦寇泽普
孙 智,冯传奇,孙建红,3,喻东明,许常悦,寇泽普
(1.南京航空航天大学航空学院飞行器环境控制与生命保障工信部重点实验室,南京210016;2.中国飞行试验研究院,西安710089;3.南京航空航天大学民航学院,南京211106;4.航空工业航宇救生装备有限公司航空防护救生技术航空科技重点实验室,襄阳441003)
飞机阻力伞是一种由柔性织物制造的气动减速设备,通常折叠放置在飞机尾部的伞仓内,在飞机着陆时被抛出并打开从而辅助机轮制动,阻力伞产生的气动阻力能够有效缩短飞机滑跑距离,增加飞机减速制动的安全性。研究表明,阻力伞可使飞机着陆滑跑距离缩短30%~40%,有效延长了机轮外胎的使用寿命,保障了飞机的着陆安全[1]。然而,随着航空部队训练的需求以及航空技术的发展,对战斗机的着陆安全提出了更高的要求,在战斗机中断起飞以及着陆过程中,飞机发动机往往会处于未完全停机状态,此时发动机喷流产生的高速射流会对阻力伞工作流场产生较大的影响,进而影响阻力伞的气动性能。因此,亟需对发动机喷流作用下的阻力伞工作过程进行研究,探究发动机喷流影响下的阻力伞气动性能,为喷流作用下阻力伞的性能评估提供理论基础。
对于单独阻力伞的研究起步较早。在20 世纪70 年代,国外就己经开始对降落伞工作过程进行数值模拟研究。降落伞的工作过程涉及非常复杂的气动弹性问题,人们从早期对降落伞充气过程的机理研究,逐步发展到对阻力伞相关流-构耦合的研究。例如,郭亮等[2]针对无人机伞回收进行了动力学分析,对无人机的整个回收过程进行仿真研究。程涵等[3]采用流-构耦合方法对某型伞低速气流下的充气过程进行了数值模拟,并对充气过程中伞衣应力、流场速度矢量、压力以及伞衣半径变化等结果进行了分析。陈猛等[4]对某五环锥伞进行了无限质量情况降落伞充气过程的流-构耦合数值模拟并进行了相关飞机减速过程开伞试验。包进进等[5]对降落伞伞包拉出过程进行了仿真研究,分析了拉出过程的载荷变化。孙建红等[6-7]采用质量阻尼弹簧模型分析了阻力伞拉直过程的引导伞阻力面积、伞系统弹性模量以及线密度等影响因素,也采用流固耦合方法对重装空投降落伞充气过程进行了仿真分析。Kimata 等[8]采用浸没边界法(Immersed boundary method,IBM)结合质量弹簧阻尼对半球壳形伞衣进行了马赫数为2 的二维和三维流固耦合数值模拟,指出二维模拟的阻力系数振荡幅度与试验相比较小,三维模拟的流场中包含分离流和重建流两种不同的流动模式。Borke 等[9]采用嵌入边界法(Embedded boundary method,EBM)对二维伞衣进行马赫数为2 的流固耦合研究,其中流场采用基于欧拉顶点的有限体积方法进行模拟,并将流场网格用自适应网格细化方法进行实时加密,结果表明在伞衣变形过程中,伞衣前方的激波能够被准确地捕捉到。薛晓鹏等[10-11]采用IBM 研究了伞绳对拖曳比为2.38 的超声速降落伞系统的影响,并采用这种方法对半球壳形伞衣进行了马赫数为2 的流固耦合数值模拟,研究了伞衣攻角和前体攻角对降落伞性能的影响。Huang等[12]采用EBM 对2 马赫的二维降落伞进行了充气过程模拟,伞绳采用主从运动学进行模拟,发现初始的折叠状态会显著改变伞衣阻力系数和最大主应力。高兴龙等[13]采用多材料任意拉格朗日-欧拉方法研究了前体的存在对超声速盘缝带伞充气过程流场的影响,得到了前体尾涡结构和伞衣周围的激波分布。蔡志军等[14]采用流固耦合方法对战斗机阻力伞载荷进行了仿真计算。杨品等[15]采用流固耦合方法对飞机阻力伞放伞过程进行了数值仿真,并对阻力伞拉直力及开伞过载等进行了分析。
上述研究主要针对阻力伞,而并未考虑发动机尾流的影响。对于发动机尾流场的研究主要关注于发动机本身以及喷流高温尾流影响区域。例如,姚金华等[16]研究了固体火箭助推器产生的高温燃气尾流场对地面发射架造成的冲刷影响。李茂等[17]针对氢氧火箭发动机地面水平试车时尾流燃气对地面热防护的影响进行了研究,并采用数值模拟方法研究了尾流场温度变化的趋势。在飞机发动机尾流场计算方面,目前的研究主要侧重于温度场模拟、测量与对流场内设备的影响及防护。如于芳芳等[18]对某型发动机尾流流场及温度场进行了数值计算,分析了不同发动机状态下的温度场特性,并研制了一套用于测量高温条件下的尾流测温系统。吴沿庆等[19]采用CFD 方法对飞机发动机尾流流场进行了数值模拟,采用反向蒙特卡洛方法对气体红外辐射特性进行了计算。黄烁桥等[20]采用试样的方法,研究了喷流对飞机尾流涡的影响。
综上可见,尽管国内外已有不少关于阻力伞和发动机喷流的研究,但鲜有对两者相互影响的相关研究,特别是针对发动机喷流作用下阻力伞的流固耦合研究。因此,本文针对不同发动机喷流速度对阻力伞的气动性能影响进行了数值仿真研究,分析了喷流速度对阻力伞阻力特性、稳定性以及流场特性的影响,为发动机喷流作用下的阻力伞性能评估和阻力伞设计提供参考。
1 数值方法
1.1 控制方程
针对发动机喷流工况下的飞机阻力伞开伞过程,本文采用了时-空守恒元解元方法(CE/SE)方法对其进行求解。其N-S 方程可以写成如下形式

式中:ρs为织物材料密度,xsi为结构单元位移。
1.2 耦合方法
文中飞机阻力伞织物间的接触以及织物结构与流场间的耦合作用基于罚函数来实现,采用具有二阶时间精度的中心差分格式对流场与结构体进行显示耦合计算,并对流体节点和结构体节点的速度以及位移进行求解,具体公式如下
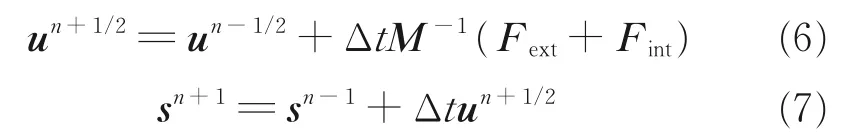
式中:u 为速度矢量;M 为质量对角矩阵;Fext为外力矢量,Fint为内力矢量,它们与体力和边界条件相关联;s 为位移矢量。
本文在流体/结构体耦合计算中使用准约束方法,对于流体部件,解算器基于欧拉方法进行求解,而对于结构部件,则基于拉格朗日方法求解。界面边界位置和速度由拉格朗日结构决定,并将该信息作为流体求解时每个时间步的界面条件,通过追踪结构和流体之间的相对位移,计算出界面力,并作为外部力的一部分对耦合区域的速度、位移进行迭代,从而实现耦合计算。
2 模型与网格
为了对发动机喷流尾流场影响下的阻力伞阻力性能进行研究,文中选取某型飞机阻力伞进行研究[14-15],阻力伞模型如图1 所示。图中,纵横交错的线条为伞衣上的加强带,伞衣臂上分布有狭小的开缝结构,缝两侧使用连接绳相连接,伞绳与加强带在伞衣底边相连,4 根加强带在伞衣顶孔处汇聚为一点。根据十字伞实际折叠过程,得到简化的十字形伞折叠模型,如图1 所示。伞衣采用SHELL 单元,伞绳及加强带采用BEAM 单元。

图1 折叠状态的阻力伞模型Fig.1 Model of drag parachute in folded state
这里以阻力伞名义直径D 为参照,选取17D(流向)×10D(展向)×10D(法向)的矩形计算域进行计算。为了准确捕捉喷流流场以及阻力伞阻力特性,对发动机喷流位置以及阻力伞位置进行局部加密,流体域网格总数约为500 万,网格如图2所示。

图2 发动机喷流中心垂直截面网格(充气状态)Fig.2 Grid of vertical section at engine center(Inflated state)
对于军用发动机,以某典型军用发动机为例,其工作状态主要可以分为:最大状态(全加力状态)、过渡状态(不加力最大推力)、额定/最大连续状态、慢车状态等工作状态。其中,额定/最大连续状态下推力为最大推力的85%~90%,连续工作时间小于30~60 min,该工作状态主要用于起飞/爬升及高速飞行;慢车状态推力为最大推力的3%~5%,主要用于下滑/进场着陆、地面滑行、地面待机等情况。某型号发动机喷流参数如表1 所示。发动机喷流作用下的阻力伞开伞主要包括中断起飞开伞和发动机未停机地面滑行开伞,这些工况下发动机一般处于慢车状态至额定状态之间。文中主要针对发动机慢车状态至额定状态下的阻力伞特性进行研究,选取对应发动机喷口的出口速度uj范围为250~500 m/s。
为了模拟发动机飞机滑行过程中发动机喷流对阻力伞阻力特性的影响,文中空气来流以及发动机喷流采用速度入口边界条件,来流速度为78 m/s,发动机喷流速度uj分别为0、250、350、500 m/s。地面为滑移壁面边界条件,滑移速度与来流速度保持一致。其余各边界均为无反射边界条件。伞绳末端节点约束在喷流入口上方位置,该位置由实际发动机喷口中心与伞系统连接点的距离决定。

表1 发动机喷流参数Table 1 Parameters of engine nozzle jet
3 计算结果与分析
3.1 发动机喷流对阻力伞阻力特性的影响
这里以飞机滑行速度78 m/s 为例,分别对发动机喷流速度分别为0、250、350、500 m/s 的喷流影响进行仿真研究。充气过程伞衣外形变化如图3 所示,来流气体在伞衣顶部聚集,随后带动伞衣迅速膨胀。经过一段时间的耦合作用后达到稳定充满状态,充满后的外形不再有大幅度变化。阻力伞充满状态不同喷流速度下的伞衣表面应力分布云图如图4 所示。由图4 可知,随着喷流速度的增大,伞衣表面应力也随之增大。
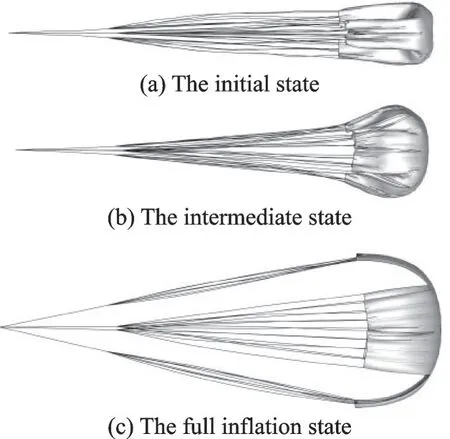
图3 阻力伞充气过程伞衣外形变化Fig.3 Changes in shape of drag parachute canopy dur-ing inflation process
为了进一步定量研究发动机喷流对阻力伞阻力特性的影响,图5 给出了不同喷流速度下阻力伞开伞过程中阻力动载F 随时间的变化曲线,表2 给出了不同喷流速度下阻力伞动载峰值Fmax以及充满状态稳态载荷(稳态平均值)F-的变化情况。通过分析可知,当无喷流时,阻力伞动载峰值出现在0.089 s,动载峰值约为126.4 kN;当喷流速度为250 m/s 时,动载峰值出现在t=0.080 s,动载峰值约为142.0 kN;当喷流速度为350 m/s 时,动载峰值出现在t=0.074 s,动载峰值约为143.4 kN;当喷流速度为500 m/s 时,动载峰值出现在t=0.070 s,动载峰值约为162.2 kN。在无喷流情况下,阻力伞充满后,稳态载荷约为64.1 kN,有发动机喷流影响时,阻力伞稳态载荷有所增大,但当喷流速度为250 m/s 时,稳态载荷约为77.8 kN,稳态载荷增加了21%;当喷流速度为350 m/s 时,稳态载荷约为97.0 kN,稳态载荷增加了51%;当喷流速度为500 m/s 时,稳态载荷约为114.8 kN,稳态载荷增加了79%。可见,随着发动机喷流速度的增大,阻力伞开伞动载峰值不断增大,并且动载峰值出现的时间不断提前,充气时间减小,稳定充气阶段的动载值也会随之增大。同时在充气初始阶段(t=0.05 s之前),开伞动载变化曲线因伞绳拉直的原因出现小幅度波动,并且喷流速度越大,其动载曲线在峰值前后的波动变化更剧烈,这会对阻力伞充气的稳定性和安全性产生一定的影响。因此,在阻力伞设计过程中,需要充分考虑发动机喷流带来的影响。
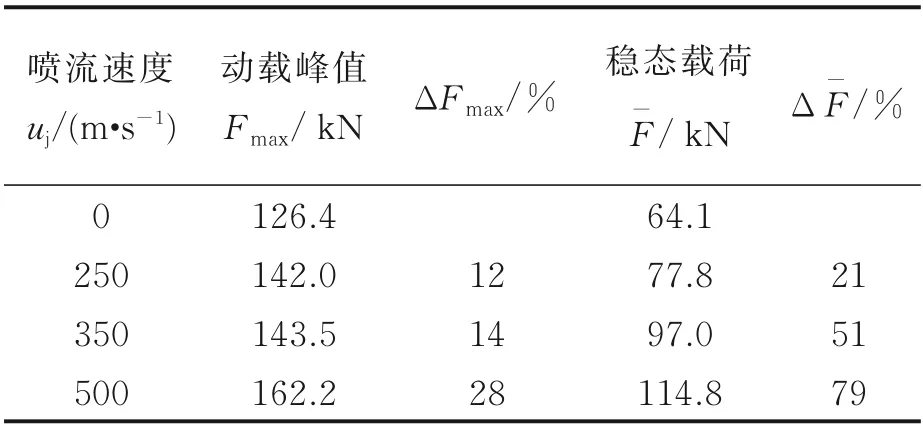
表2 发动机喷流影响下的阻力伞阻力特性Table 2 Drag characteristics of drag parachute under different jet velocities
3.2 发动机喷流对阻力伞稳定性的影响
稳定性是阻力伞的另一个重要性能参数,如果工作过程中阻力伞的摆动幅度过大,可能会使得阻力伞拖地,进而出现破损。因此,文中选取阻力伞在垂直方向的摆动距离进行分析研究。图6 给出了不同喷流速度下,十字形阻力伞顶点(即径向加强带在伞顶孔处的交汇点)在开伞充气过程中垂直方向(Y 方向)上的位移随开伞过程的变化曲线。从图中可以看出,由于发动机喷流的高速吹袭作用,阻力伞会向下偏斜,当喷流速度为250 m/s 时,阻力伞顶点向下偏斜位移为0.41 m;当喷流速度为350 m/s 时,阻力伞顶点向下偏斜位移为0.65 m;当喷流速度为500 m/s 时,阻力伞顶点向下偏斜位移为0.73 m 。通过对比发现,由于发动机喷流喷口中心位置高度H 为1.85 m,喷口位置在阻力伞下方(阻力伞初始中心位置高度H 为3 m),高速的发动机喷流气流主要吹袭到十字形阻力伞靠近地面的伞衣区域,伞衣靠近地面内侧压力偏大,伞衣会产生向下的偏向力。同时,高速气流流经伞与地面中间时,会产生一定的“狭管效应”,使得靠近地面伞衣外侧的压力降低,进一步增加伞衣向下的偏移。在阻力伞顶点向下位移到最大位置后,在伞绳向上分力的作用下又迅速向上偏移,形成一种上下往复的周期性振荡,并且摆动的幅度随着喷流速度的增大而增大,同时偏斜发生的时间也随着喷流速度的增大而前移。所以发动机喷流速度对阻力伞的稳定性有一定的影响,喷流速度越大,阻力伞摆动振幅越大,阻力伞稳定性越差。
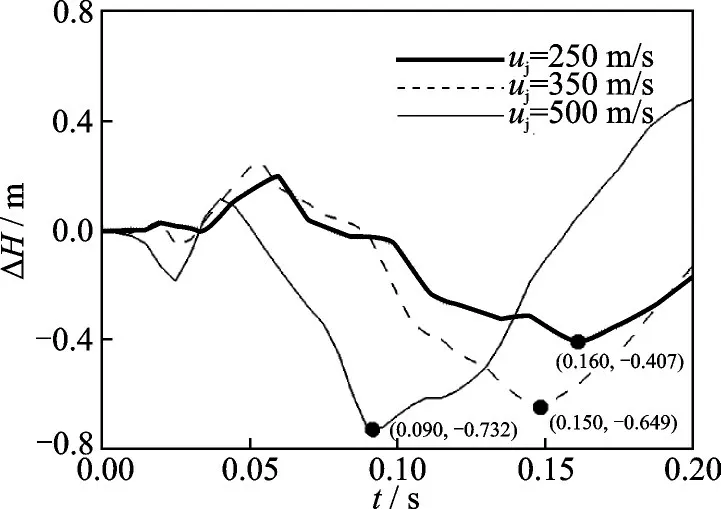
图6 不同喷流速度下阻力伞垂直方向摆幅随开伞过程的变化Fig.6 Change of vertical displacement of drag para-chute during inflation process under different jet velocities
3.3 发动机喷流作用下的阻力伞流场特性分析
为了进一步研究发动机喷流对阻力伞阻力特性以及摆动稳定性的影响,文中对不同发动机喷流情况下的阻力伞充满状态流场特性进行研究。图7 为充满状态t= 0.2 s 时刻不同喷流速度中心截面上的速度分布。由图可知,当发动机尾喷存在时,阻力伞伞前流场的速度比无发动机尾喷时要大,并且随着喷流速度的增加,阻力伞前的流场速度也逐渐增大。发动机喷流吹袭到阻力伞伞衣偏下位置,会导致阻力伞伞衣膨胀程度更大。同时,喷流气流在流经阻力伞伞衣与地面形成的狭小通道时被加速,产生一定的“狭管效应”,使得伞衣向地面偏移,这种气流加速的“狭管效应”会随着发动机喷流速度的增加而越发明显。
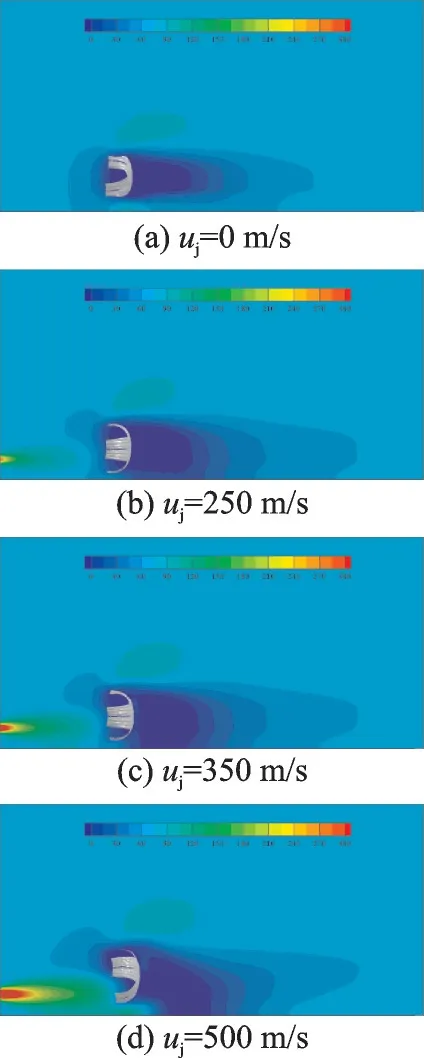
图7 不同喷流速度下阻力伞充满状态垂直中心截面速度云图Fig.7 Velocity distribution of vertical center section of drag parachute in inflated state under different jet velocities
通过阻力伞充满状态垂直中心截面上的速度分布云图可以对发动机喷流对阻力伞流场特性的影响有一个定性的认识。为了进一步定量分析阻力伞流场特性,文中选取了发动机喷流中心线(H=1.85 m),阻力伞初始中心线(H =3 m)以及阻力伞前x=3、6、9 m 三条垂直线进行分析,具体位置如图8 所示。不同喷流速度下发动机喷流中心线上的速度uce分布如图9 所示。由图可知,高速的气流从发动机喷出后快速衰减,经过阻力伞后速度出现负值,产生一定的回流区,随后速度又逐步回升,最后与来流速度基本一致。通过不同喷流速度之间的对比可以发现,喷流速度越大,阻力伞之前的来流速度也越大,这也是喷流状态下阻力伞阻力增大的原因。
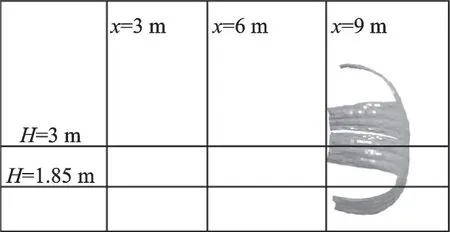
图8 阻力伞充满状态垂直中心截面特征线位置示意图Fig.8 Schematic diagram of characteristic line position of vertical center section in inflated state
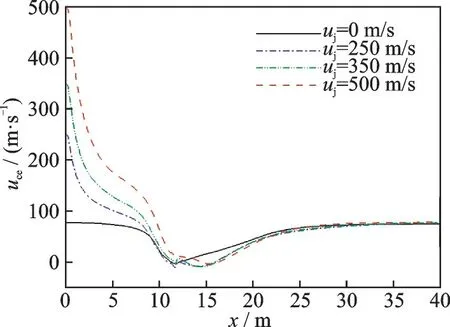
图9 阻力伞充满状态下发动机喷流中心线上的速度变化曲线(H=1.85 m)Fig.9 Speed curve on centerline of engine nozzle in inflated state(H=1.85 m)
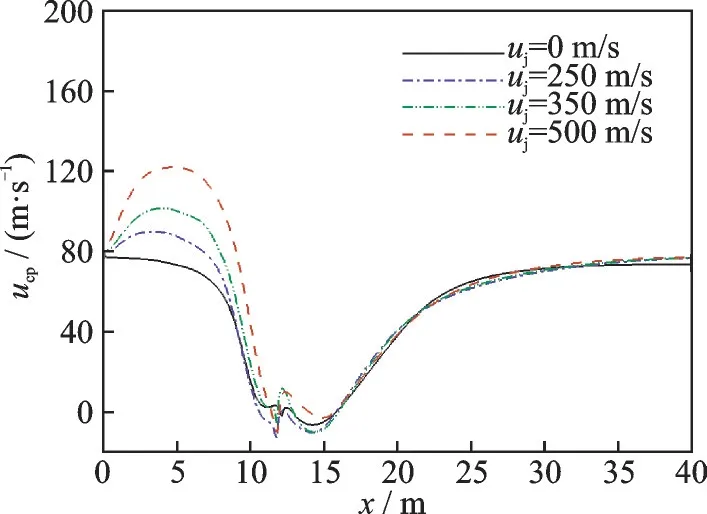
图10 阻力伞充满状态下伞中心线上的速度变化曲线(H =3 m)Fig.10 Speed curve on centerline of drag parachute in inflated state(H =3 m)
不同喷流速度下阻力伞中心线上的速度ucp分布如图10 所示。由图可知,起始速度为来流速度,随后由于高速喷流的卷吸作用,速度逐步升高,随后又快速衰减,经过阻力伞后同样会出现回流区,最后气流速度逐步回升至来流大小。此高度上的阻力伞前来流速度会略小于喷流中心线上的气流速度,但总体上仍大于无喷流状态下的伞前速度。
阻力伞伞前不同垂直线上(x=3、6、9 m)上的速度分布如图11 所示。由图可知,喷流速度沿喷流中心衰减,且随着流向距离的增加,喷流的速度也逐步减小,喷流的影响区域主要集中在0~4 m的范围内,阻力伞大部分伞衣都在该范围之内,因此,喷流对阻力伞的性能会产生影响。通过x=9 m 处气流速度随高度的变化曲线可以发现,在靠近地面(阻力伞与地面之间)部分的气流速度有明显提升,这进一步佐证了气流使得伞衣向下偏转。
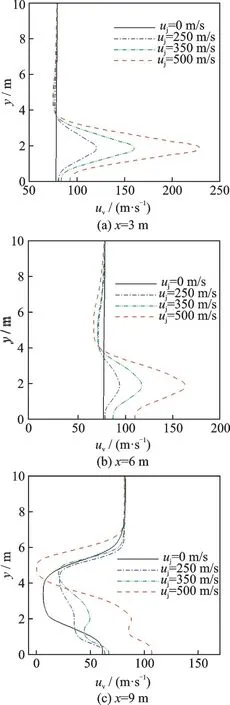
图11 阻力伞充满状态时不同垂直线上的速度变化曲线(x=3,6,9 m)Fig.11 Speed curve at different distances in inflated state (x=3,6,9 m)
图12 给出了充满状态t=0.2 s 时刻不同喷流速度中心截面上的压力分布。由图可知,在阻力伞工作过程中,伞衣内侧压力升高,阻力伞后方会形成一定的低压区,当存在发动机喷流时,阻力伞内侧的高压区压力变大,且伞衣内侧下方的压力偏高,随着喷流速度的增大,这种效果更加明显,这种上下不对称的伞衣压力分布使得阻力伞产生向下偏转力,使得阻力伞出现上下偏转的现象。图13~14 分别给出了发动机喷流中心线和阻力伞初始中心线上的压力(Pce,Pcp)变化曲线。由图可知,气流经过阻力伞后,压力急速降低,出现一定的低压区。通过对比不同喷流速度下的压力分布可知,在伞前以及伞内侧的压力会随着喷流速度的增大而增大,从而使得伞衣的阻力更大,伞衣充满程度更明显。
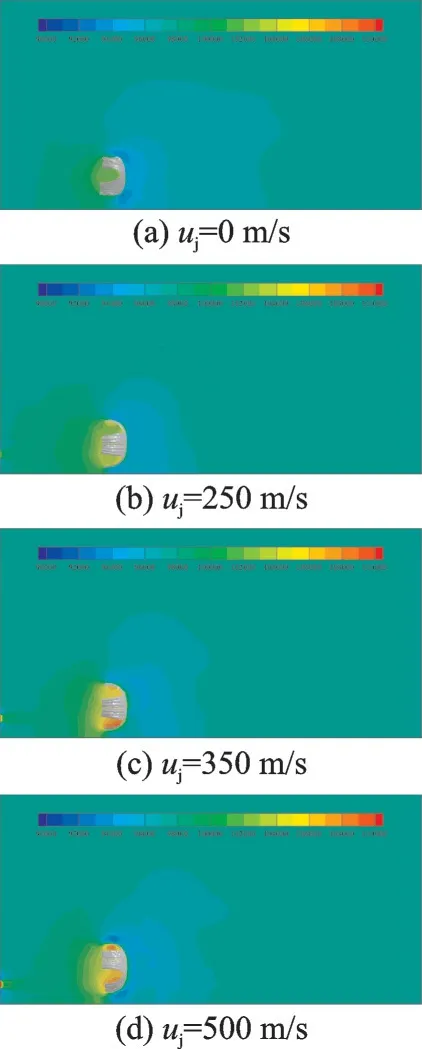
图12 不同喷流速度下阻力伞充满状态垂直中心截面压力云图Fig.12 Pressure distribution of vertical center section of drag parachute in inflated state under differ-ent jet velocities
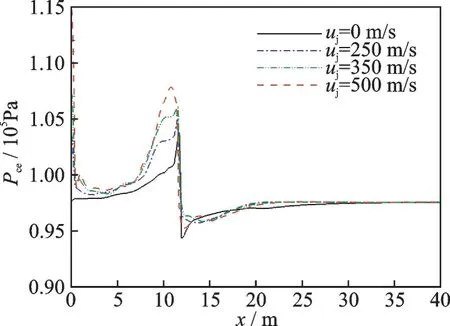
图13 阻力伞充满状态时发动机喷流中心线上的压力变化曲线(H=1.85 m)Fig.13 Pressure curve on centerline of engine nozzle in in-flated state(H=1.85 m)
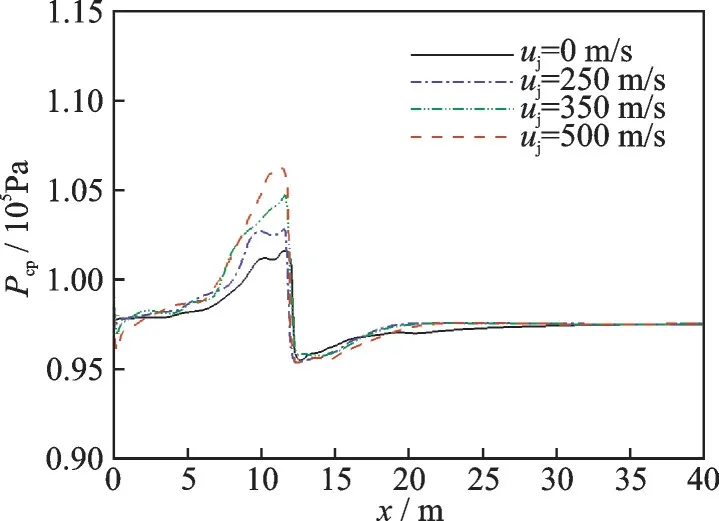
图14 阻力伞充满状态时伞中心线上的压力变化曲线(H=1.85 m)Fig.14 Pressure curve on centerline of drag parachute in in-flated state(H=1.85 m)
4 结 论
本文对不同发动机喷流速度下的阻力伞开伞过程进行数值仿真研究,分析了不同喷流速度对阻力伞阻力特性、阻力伞稳定性以及流场特性的影响,主要结论如下:
(1)发动机喷流会使得阻力伞伞前的流体速度变大,导致阻力伞开伞动载峰值出现时刻前移,开伞动载峰值变大,充满状态的阻力伞稳态载荷变大。
(2)喷流速度为250 m/s 时,稳态载荷增加21%;当喷流速度为350 m/s 时,稳态载荷增加51%;当喷流速度为500 m/s 时,稳态载荷增加79%。
(3)发动机喷流会使得伞衣内侧下方的压力偏大,伞衣压力分布不对称,从而使得阻力伞发生上下摆动,且喷流速度越大,阻力伞摆动振幅越大,阻力伞稳定性越差。
