高山松单木地上生物量模型不确定性研究

王柯人 舒清态 赵洪莹 谭德宏 袁梓健

（西南林业大学林学院，云南 昆明 650233）

森林作为“地球之肺”，其生物量的估测、监测和评价一直是学术界的关注热点，其中生物量估测的建模发挥着重要作用。国内外关于森林地上生物量估算的方法众多：基于单木水平生物量模型构建[1-2]、基于林分生物量模型构建[3-5]。在建立单木地上生物量模型时，为评价模型拟合优度，国内外学者采用确定系数（R2）、估计值的标准差（SEE）、平均系统误差（MSE）及总相对误差（TRE）等[6]。

关于单木地上生物量模型建立过程中的不确定性来源一般分为三方面：抽样误差、模型误差和测量误差[7]。Shettles等[8]认为，模型误差在3种误差来源中所占比重最大。鉴于此，本研究重点为模型误差的分析。模型误差来源分为四方面：变量本身的误差、残差变异性、参数估计产生的误差、所选择模型的误差[9-10]。当前国内外关于模型的误差分析集中于多个模型精度评价和比较[1,11-12]，变量本身的误差分析，也就是测量过程中误差分析[13-14]，关于模型参数不确定性及残差变异性分析常被忽略。王仲锋等[15]认为采用非线性最小二乘回归法求解单木地上生物量幂函数的参数及参数协方差矩阵，可获得较高精度，对模型参数不确定进行分析。傅煜等[16-17]认为对于非线性模型，运用泰勒级数一阶展开项度量非线性模型的参数误差可以取得较好的效果。如何计算量化多种多样的不确定性以提高森林地上生物量估算的精确度已成为当前研究的重要挑战。

本研究以云南省香格里拉市为研究区，基于香格里拉市2016年森林资源二类调查数据，通过建立一元、二元地上生物量模型来估算高山松（Pinus densata）单木地上生物量[18-19]，并分析了2种模型的不确定性，以期为提高高山松森林地上生物量估测精度提供参考。

1 研究区概况

香格里拉市位于云南省西北部（99°23′06.08″～

100°18′29.15″E，26°52′11.44″～28°50′59.57″N），总面积114.2万hm2，东、南、西三面被金沙江环绕，是滇、川、藏三省区交界地，也是世界自然遗产“三江并流”景区所在地。主要地貌类型为山地，地形总趋势西北高、东南低，海拔为1 503～5 545 m。区域内高山松作为我国西南部香格里拉地区及青藏高原地区的特有森林建群种，起源于油松（Pinus tabuliformis）与云南松（Pinus yunnanensis）的天然同倍体杂种，在高山地区形成大面积纯林，对保持高原森林生态环境有十分重要的意义[19]。

2 材料与方法

2.1 高山松单木数据

研究所使用的113株高山松地上部分生物量数据通过收获法获取，并测量单木胸径（DBH）、树高（H）以及木材、树皮、树枝及树叶鲜质量，分别抽样带回实验室，在85 ℃下恒温烘干至恒质量，称量样本干质量，换算得出样木各组分干质量，汇总得出立木地上生物量。高山松单木建模数据统计特征见表1。单木各部分生物量数据中，单木胸径在每个径阶分布不均，单木地上生物量最大值为2 058.5 kg，最小值为4.03 kg。单木各个部分生物量平均值及标准差差异显著，干材生物量平均值及标准差最高，树叶生物量平均值及标准差最低。

表 1 高山松单木建模数据统计特征Table 1 Statistical characteristics of modelling data sets

2.2 生物量模型的构建

已有研究表明，幂函数在针叶林生物量模型构建中效果较好[1-3]。本研究基于幂函数进行高山松单木地上生物量模型构建，分别采用胸径单变量和胸径−树高进行拟合，并采用最小二乘法求解公式中的参数采用最小二乘法求解公式中的参数，计算公式由式（1）、（2）表示。

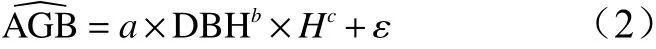
2.3 模型误差变异不确定性分析

回归模型建立过程中，利用残差值表示回归分析中测量值与方程预测值的差值来反映生物量模型拟合的效果[18]，如式（1）、（2），则模型误差可表示为：

研究发现，残差的标准差随单木地上生物量的增加而增加，呈线性关系[9]。即：

式中：μ为残差值的标准差，β为拟合参数。

在计算μ时，本研究采用六步法计算[20]，将单木地上生物量的实测值AGB进行升序排列，计算预测值及残差值ε，再以n个样本为一组，若最后一组不足n，则计入上一组，n取5、8、10。最后计算每组数据生物量预测值的平均值及残差的标准差με，此时，对于生物量预测值的平均值、残差值的标准差和拟合参数可通过下式计算：

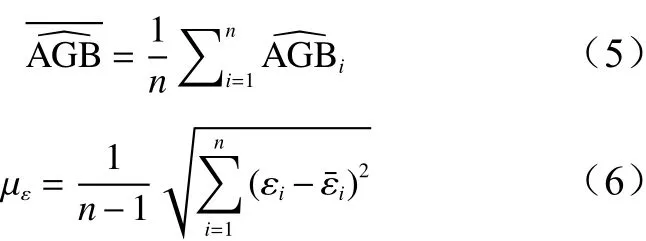
2.4 模型参数对生物量模型估计不确定性分析

采用非线性最小二乘法的原理求解单木高山松地上生物量模型参数a、b、c。参数引起的不确定性，可以采用泰勒级数对式（1）、式（2）展开[9-10,16]。则有：

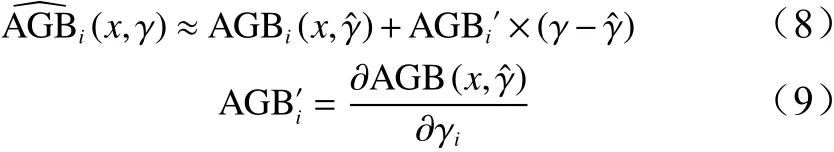
式中： AGBi(x,γ)中参数γ可反映最近似真实值的

2.5 模型不确定性合成

模型误差指在生物量模型估计中的误差，其中最主要的是模型残差变异不确定性和模型参数估测误差。由已有研究可知，生物量模型估测中不确定性来源于抽样误差和单木生物量外推时传播并累计下来的误差，并具有传递性[17,21-22]。因此高山松单木地上生物量估测模型综合不确定性（ξ）可通过模型残差变异性和模型参数估测误差来表示：

式中：β为模型残差不确定值，δF为地上生物量模型参数引起的模型估测误差。

3 结果与分析

3.1 生物量模型评价

本研究以高山松单木胸径以及树高和胸径组合分别构建一元和二元回归模型，结果见表2。由表2可知，2个模型回归系数以及调整后的回归系数（Radj2）均大于0.9，说明模型拟合效果较好；二元地上生物量模型调整回归系数、均方根误差（RMSE）均优于一元地上生物量模型。根据生物量建模数据绘制单木地上生物量、胸径及树高散点图见图1～2。由图1可知，高山松单木建模数据集中于胸径0～30 cm，高山松胸径小于20 cm时，地上生物量增长缓慢，当胸径大于30 cm，地上生物量呈上升状态，且增长速率增大。由图2可知，单木树高、胸径和地上生物量呈明显的线性关系。

表 2 单木生物量模型的构建Table 2 Construction of individual biomass model

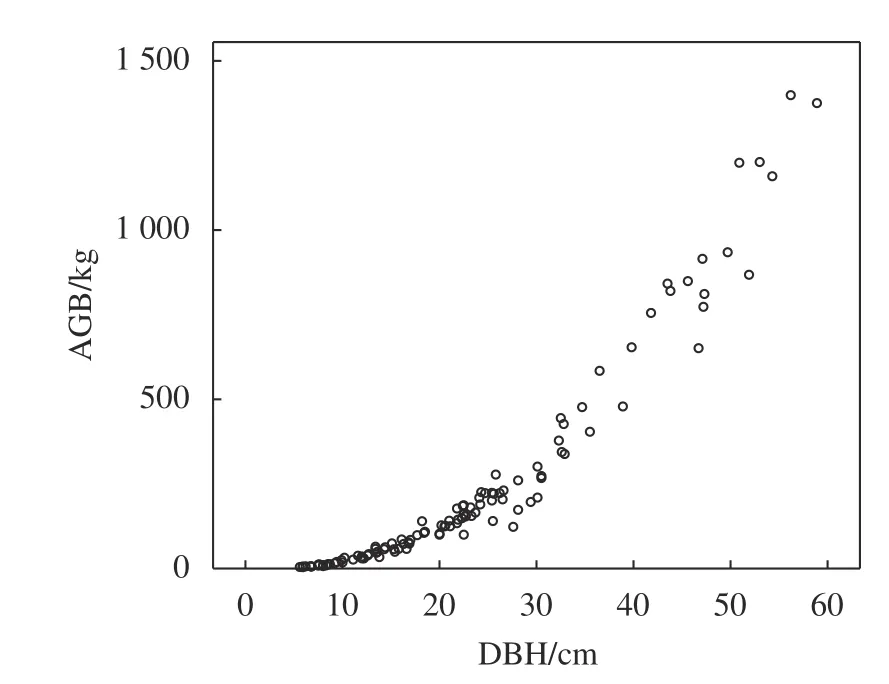
图 1 高山松一元地上生物量模型Fig.1 Univariate biomass model ofP. densata

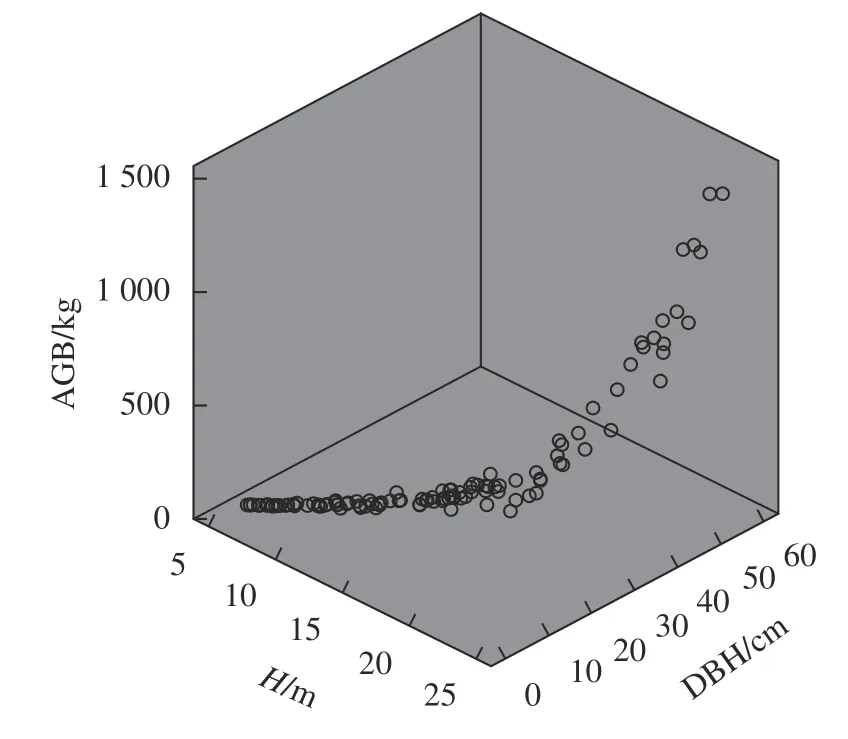
图 2 高山松二元地上生物量模型Fig.2 Binary biomass model ofP. densata

3.2 一元地上生物量模型的不确定性分析

3.2.1 模型的残差变异不确定性分析

根据模型残差标准差与预测值的散点图（图3），一元单木地上生物量模型残差变异引起的不确定性可表示为：0.615。对于一元地上生物量模型，由模型残差变异引起的不确定性约为6.20%。

图 3 残差值的标准差与高山松生物量预测值的关系Fig.3 The relationship between the SD of the residuals and biomass prediction

3.2.2 模型参数对生物量模型估计不确定性分析

一元地上生物量模型参数对生物量模型估计的不确定性在MATLAB下将一元地上生物量回归模型经过泰勒级数展开后求得灵敏度系数矩阵，也就是参数的协方差矩阵，可求得参数不确定性。其中，一元模型参数的协方差矩阵为可求得一元模型中由于模型参数带来的不确定性δ=30.20%。根据残差变异不确定性及参数不确定性进行不确定性合成，因此高山松单木一元地上生物量模型的综合不确定性约为30.83%。

3.3 二元地上生物量模型的不确定性分析

3.3.1 模型的残差变异不确定性分析

根据二元模型残差值的标准差与预测值的变化，由图4可知，从图中可看出残差值的标准差随着单木地上生物量预测的增加而增加，与一元地上生物量模型的残差标准差与单木地上生物量变化的趋势相同。其变化规律可表示为：因此对于二元地上生物量模型而言，由模型残差变异引起的不确定性约为5.17%。

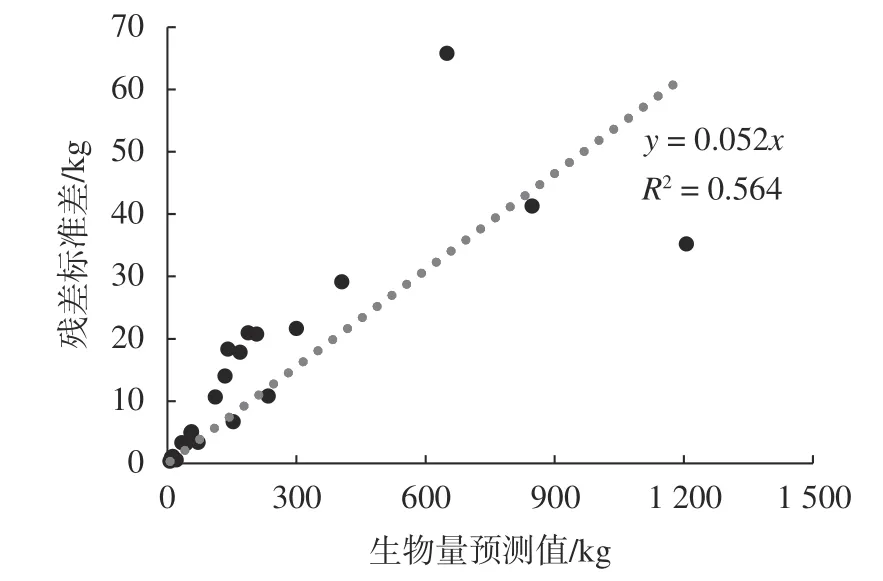
图 4 残差的标准差与高山松生物量预测值的关系Fig.4 The relationship between the SD of the residuals and biomass prediction

3.3.2 模型参数对生物量模型估计不确定性分析

将二元地上生物量回归模型经过泰勒级数展开后求得灵敏度系数矩阵得到二元模型参数的协方差矩阵可

求得二元地上生物量模型的参数不确定性δ=3.12%。根据参数不确定性进行不确定性及残差变异不确定性合成，因此高山松单木二元地上生物量模型的综合不确定性约为6.04%。

3.4 建模样木数量及分组方式对模型不确定性的影响

由于建模样本数量一定程度反映了模型的适应性和可拓展性，本研究使用了113株样木数据建模，为探究建模样本数对模型构建的影响，本研究总样本数（N）为113，随机抽取了N/3、2N/3的样本量，计算不同样本量条件下的模型参数不确定性。其次，对比相关研究来看，不同分组样本数对模型残差的不确定性也有一定影响，为探究不同分组数据对模型残差变异的影响，本研究还探讨了5株一组、8株一组、10株一组的分组方式进行残差不确定性变化分析，结果见表3。

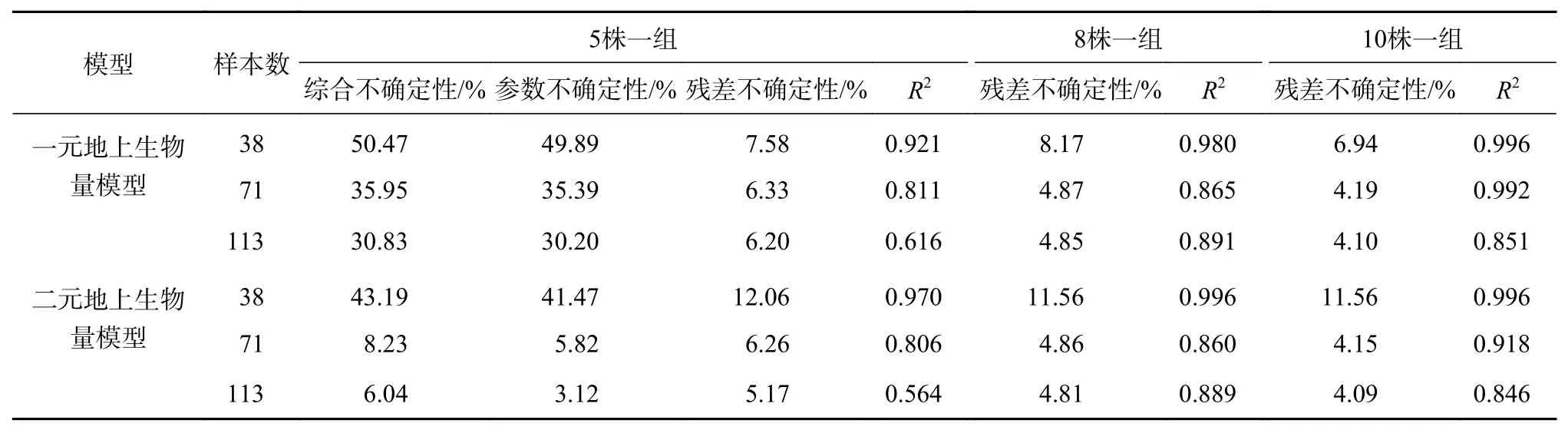
表 3 不同建模样木数量及分组方式对模型不确定性影响Table 3 Model uncertainty influence of different modeling sample quantity and grouping methods

由表3可知，当分组样本数为5时，二元地上生物量模型的残差变异不确定性、参数不确定性及综合不确定性均优于一元模型，且模型参数引起的不确定性大于模型残差变异不确定性。基于113株高山松单木生物量构建一元地上生物量模型中由模型参数引起的不确定性为30.30%，模型残差变异引起的不确定性约为5.17%，综合不确定性约为30.83%；二元回归模型中由模型参数不确定性为3.12%，残差变异引起的不确定性约为6.18%，综合不确定性约为6.94%；随着样本量的增加，模型的参数不确定性及残差变异不确定性逐渐减小，当建模样本量从38增加至71时，模型的不确定性变化显著，一元模型的参数不确定性和残差变异不确定分别由49.89%和7.58%降低至35.39%和6.33%，综合不确定性减少14.52%；二元模型参数不确定性和残差变异不确定分别由41.47%和12.06%降低至5.82%和6.26%，综合不确定性减少34.96%；当样本数量大于71以后，模型不确定变化逐渐减小。分析得出一元地上生物量模型由单一变量构建，没有考虑到树高对于生物量估测的影响，因此一元地上生物量模型参数误差引起的不确定性显著高于二元地上生物量模型。

上述结果表明随着样本量的增加，模型的残差变异不确定性逐渐减小；同时，随着分组样本数的增加，无论一元地上生物量模型和二元地上生物量模型，其模型的残差变异不确定性也逐渐减小，虽呈现出一定的规律，但差异并不是很明显，当分组样本数分别为5株一组、8株一组、10株一组，一元地上生物量模型残差变异不确定性分别为6.20%、4.85%、4.10%，二元地上生物量模型残差变异不确定性分别为6.18%、4.81%、4.09%。分析得出，样本数量较少时，分组的数量对于模型残差变异不确定性有所影响，但影响较小，在计算模型残差变异不确定性进行分组时应考虑样本总量。

4 结论与讨论

本研究基于113株香格里拉高山松单木地上生物量实测数据建立一元、二元地上生物量模型，并通过六步法计算模型残差变异不确定性，泰勒级数展开式对模型参数不确定性进行计算，进行模型的参数及残差变异的不确定性量化。通过分析得出以下结论：

1）二元地上生物量模型的残差变异不确定性、参数不确定性及综合不确定性均优于一元模型，且模型参数引起的不确定性大于模型残差变异不确定性，随着样本量的增加，模型的参数不确定性及残差变异不确定性逐渐减小，当样本数为113时，生物量模型的不确定性最小。

2）随着分组样本数的增加，无论一元地上生物量模型和二元地上生物量模型，其模型的残差变异不确定性也逐渐减小。

3）模型残差变异不确定性和参数不确定性是单木地上生物量模型构建中不确定性的主要来源，增加模型参量能有效降低单木地上生物量模型中参数引起的不确定性。

本研究所使用的单木建模数据来源于香格里拉2个高山松天然林样地，单木胸径范围为5.6～58.9 cm，胸径均值为23.3 cm，标准差为13.03 cm，单木胸径在每个径阶分布不均。在计算一元、二元模型残差变异不确定时，当单株预测生物量介于500～1 500 kg时，残差的标准差值产生较大波动，对残差变异不确定性计算产生较大影响。本研究结果中的参数误差引起的不确定性高于傅煜等[16,22]、Chen等[23]的研究，其原因主要为傅煜等使用了150株杉木作为建模样本，并在模型分析法中引入了Monte Carlo法对模型进行了1 000次模拟，其有效降低了参数协方差矩阵的变异性，对参数残差引起的不确定性度量更为准确；Chen等[23]采用了4 004株样木进行建模，远高于本研究，说明当样本量足够大时，参数误差引起的不确定性趋近于零；其次，本研究基于113株高山松为样本对高山松地上生物量估算不确定性分析，并在此基础选取了总样本量的1/3、2/3进行对比分析，可看出当建模样本量从38增加至71时，模型的综合不确定性变化显著，而当建模样本数量大于71以后，模型的综合不确定变化趋于平缓。说明样本量的增加能显著降低模型残差变异不确定性，参数不确定性以及模型综合不确定性，该结果与秦立厚等[9,21]的研究结果一致，但建模最优样本量还待今后进一步分析。

模型误差来源分为四个方面，其中变量本身的误差和所选择模型的误差已有较多研究。赵平安等[13]基于临安市森林资源清查样地数据和临时样地调查数据得出对于地上碳储估算，误差占比最大的为抽样误差和遥感影像坐标校正定位误差。曾伟生等[24]的研究基于150株落叶松和马尾松的立木生物量实测数据，对地下生物量模型的一元、二元回归模型方案进行对比分析，得到马尾松地下生物量模型估测精度可达90%以上，落叶松可达85%以上。本研究仅对残差变异性和参数估计产生的误差进行了计算，未对另外两方面进行分析，今后还需进一步研究。