多管火箭武器箱式复合材料定向器长期堆码贮存吸湿- 蠕变耦合行为预测

孙同生， 朱隽垚， 于存贵， 杨文超， 徐强

(1.南京理工大学 机械工程学院, 江苏 南京 210094；2.湖北江山重工有限责任公司 火箭炮研究院, 湖北 襄阳 441057；3.江西长江化工有限责任公司, 江西 九江 332006)

0 引言

为了提高多管火箭武器的快速响应能力和连续作战能力，现役以及在研的多管火箭武器大多都采用储运发射箱式复合材料定向器。纤维增强环氧树脂基复合材料具有高的比强度、比刚度、优良的耐腐蚀性能和相对低廉的价格等优点[1-2]，可以满足储运发射箱减重、节约资源和成本的要求。然而，聚合物基体的存在使得纤维增强聚合物基复合材料的力学行为具有强烈的时间和环境依赖性，表现出黏弹性力学特性，当应力超过线性阈值时或在高温、高湿环境中会呈现非线性特征[3]。因此，箱式复合材料定向器在仓库长期带弹堆码贮存过程中，受载荷和环境的综合作用会出现蠕变变形，从而对火箭弹的发射产生不利影响。

在各种服役环境中，湿热是普遍存在且对复合材料力学性能影响最大的环境因素[4-6]。聚合物基体以及纤维- 基体界面吸收环境中的水分，不仅会引起准静态强度和弹性模量的下降，还会显著增加蠕变速率[7]。刘建华等[8]在实验室模拟海洋大气环境进行加速老化试验，发现玻璃纤维增强环氧树脂基复合材料的拉伸、压缩和层间剪切强度随吸湿率的增加而下降，并且当吸湿率达到一定程度后，力学性能基本保持不变，反映出力学性能与吸湿率之间存在一定的对应关系。Haddar等[9]研究了短切玻璃纤维增强聚酰胺复合材料在湿环境中的老化行为，发现复合材料的弹性模量和强度随着吸湿率的增加而下降，下降规律与吸湿规律相对应。

关于吸湿对复合材料黏弹性性能的影响，许家宝等[10]通过热机械动力学分析(DMTA)方法研究了吸湿率对玻璃与亚麻纤维混杂复合材料动态黏弹性性能的影响，结果表明：储能抗弯刚度随着吸湿率的增加而降低，而耗散抗弯刚度随着吸湿率的增加而增加；在吸湿前期储能抗弯刚度的下降速度较大，在吸湿后期下降速度减缓，这一现象与复合材料的吸湿增重规律类似。高禹等[11]研究了湿热老化对HT280双马来酰亚胺树脂蠕变性能的影响，结果表明长期湿热老化会导致树脂抗蠕变性能下降。Kontaxis等[12]对比了干态和湿态试样的弯曲蠕变- 回复行为，发现蠕变应变随着吸湿时间的增加而增加。Wang等[13]通过试验研究发现湿环境暴露对基体主导的黏弹性性能有显著影响。Guedes等[14]研究发现吸湿对复合材料小试样的初始刚度和黏弹性力学行为有显著影响，并且当吸湿温度低于玻璃化转变温度时，吸湿温度不会明显影响试样的力学性能。

复合材料结构在实际服役过程中的长期力学行为是一个复杂的多场耦合问题，吸湿、力学性能退化以及蠕变同时进行，相互影响。随着多场耦合有限元建模技术的发展，越来越多的研究人员利用有限元方法预测结构的长期服役力学行为[15-17]。本文通过理论推导、试验研究和有限元数值模拟相结合的方法，研究箱式复合材料定向器长期带弹堆码贮存的蠕变变形问题。首先，在Schapery单积分型非线性蠕变模型中引入与吸湿率相关的移位因子，表征吸湿对复合材料蠕变行为的影响，建立三维正交各向异性非线性蠕变本构模型。其次，制备E-玻璃纤维/6509环氧树脂复合材料层合板，开展吸湿老化试验和短期拉伸蠕变- 回复试验，获得复合材料吸湿特性参数、力学性能退化规律以及Schapery非线性参数随吸湿率和应力的变化规律；最后，将本构模型转换为增量迭代形式，编写用户自定义材料(UMAT)子程序和用户自定义场变量(USDFLD)子程序，建立吸湿- 蠕变耦合三维有限元模型，预测箱式复合材料定向器长期贮存15 a后的蠕变变形。

1 理论模型

1.1 考虑吸湿效应的Schapery非线性模型

根据不可逆热动力学理论，Schapery推导出等温条件下单轴载荷作用时的单积分型非线性蠕变模型[18-19]为

(1)

式中：ε(t)为t时刻的总应变，t为时间；D0为瞬时弹性柔量；σ(t)为t时刻的应力；σ(τ)为0～t时间段内与τ时刻对应的应力，τ为积分时间符号；ψt和ψτ为折算时间，

(2)

ξ为积分符号；g0、g1、g2和aσ为与应力相关的非线性参数，通常表示为基体八面体剪应τo的函数[4]，当g0=g1=g2=aσ=1时(1)式退化为线性模型； ΔD(·)表示线性瞬时蠕变柔量函数，可以根据广义Kelvin模型来获得[20]，

(3)

N为Kelvin单元的总个数，Dn为第n个Kelvin单元的弹性柔量，λn为第n个Kelvin单元的阻尼系数，Df为稳定流动分量。

在构建考虑吸湿响应的非线性蠕变本构模型之前，作出如下假设：1)吸湿不会影响线性瞬时蠕变柔量，仅通过与吸湿率相关的移位因子对非线性黏弹性产生影响；2)吸湿率相关的移位因子与应力相关的Schapery非线性参数之间不存在耦合关系。

基于以上假设，忽略吸湿引起的溶胀应变，得到考虑吸湿效应的Schapery非线性模型如下：

(4)

式中：

(5)

非线性参数g0m=g0a0m，g1m=g1a1m，g2m=g2a2m，aσm=aσaσm，a0m、a1m、a2m和aσm为与吸湿率相关的移位因子，对于干态材料，a0m=a1m=a2m=aσm=1.

1.2 三维正交各向异性非线性蠕变本构模型

通常认为单向纤维复合材料内部的纤维呈均匀分布，即单向复合材料为正交各向异性材料。则在局部材料坐标系下，考虑蠕变应变的三维正交各向异性本构模型为

σ=D(ε-εc)，

(6)

式中：σ为应力矩阵；D为弹性刚度矩阵；ε为总应变列阵；εc为非线性蠕变应变列阵。

由于玻璃纤维不具有黏弹性，复合材料纵向力学行为与时间无关，而基体性能主导的横向和剪切方向上的力学性能与时间相关，表现出黏弹性效应。因此，

(7)

(8)

2 试验设计

2.1 试验材料

试验用原材料为G20000型E-玻纤/6509环氧树脂单向预浸料，名义厚度为0.17 mm，单位面积质量为200 g/m2，纤维体积含量约为65%，由威海光威复材有限责任公司提供。

复合材料层压板采用模压工艺制备，固化工艺为：120 ℃，2 MPa条件下保温、保压2 h后，冷却至室温脱模。切割得到复合材料试样的种类及尺寸如表1所示。其中，采用100 mm×100 mm方形试样测试复合材料的吸湿性能。

表1 试样种类及尺寸Tab.1 Types and sizes of GFRP specimens

2.2 试验方法

2.2.1 吸湿试验

吸湿称重试验按照美国材料试验协会标准ASTM D5229-14聚合物基复合材料吸湿性能和吸湿平衡条件的标准测试方法[21]开展。试验前将试样放入南京沃环科技实业有限公司产WH101-2A(S)型电热鼓风干燥箱，在50 ℃条件下烘干96 h后保存在铝塑封袋中备用。吸湿试验在南京环科试验设备有限公司产GDJS-010A型恒温恒湿试验箱中进行，试验工况如表2所示。根据国家军用标准GJB 2770—1996军用物资贮存环境条件[22]，以一般条件军用仓库(Ⅲ级仓库)作为箱式定向器的长期贮存场所，选择该等级仓库最高温、湿度条件设为工况C1，测试定向器材料的湿扩散系数和平衡吸湿率。工况C2为加速试验环境，目的是对蠕变- 回复试样进行吸湿预处理。

表2 试验工况Tab.2 Test conditions

试验过程中，每间隔一定时间取出试样，用奥豪斯仪器有限公司产AR124CN型高精度(0.1 mg)电子天平称重，并根据(9)式计算吸湿率，

(9)

式中：Mt为t时刻吸湿率(%)；wt为t时刻试样的质量(g)；w0为试样烘干后的初始质量(g)。

根据Fick第二扩散定律，利用吸湿曲线的初始直线段计算得到湿扩散系数，计算公式[6]如下：

(10)

式中：D为湿扩散系数；h为试样厚度；Mm为平衡吸湿率；M1、M2为吸湿曲线初始线性段上对应t1、t2时刻的吸湿率。

2.2.2 静态力学性能测试

分别按照美国材料试验协会标准ASTM D3039/3039M-14 聚合物基复合材料拉伸性能试验方法[23]和ASTM D3518/3518M-13 用±45°层合板拉伸测定聚合物聚合物基复合材料面内剪切性能试验方法[24]，在深圳三思纵横科技股份有限公司产UTM5105-G型电子万能材料试验机上，针对不同吸湿量的复合材料试样开展拉伸和面内剪切试验，加载速度为2 mm/min. 利用汉中精测电气有限责任公司产BF120-3AA型电阻应变片、江苏联能电子技术有限公司产YE3818C型动态应变仪、YE29003A型桥盒、美国国家仪器有限公司产NI9215型数据采集器测试并记录试样的应变值，采样频率为10 Hz. 每组试样测5个，取其平均值。试验测试系统如图1所示。

图1 试验测试系统Fig.1 Experimental testing system

2.2.3 拉伸蠕变- 回复试验

参考日本工业标准JIS K 7078—1996碳纤维增强塑料拉伸蠕变试验方法[25]，在室温环境下，采用1 h蠕变/1 h回复的方式开展短期拉伸蠕变- 回复试验，其中，横向上共包括7个应力水平，分别为横向干态拉伸强度的35%、41%、47%、53%、60%、66%和72%；面内剪切方向上共包括8个应力水平，分别为干态剪切强度的19%、25%、31%、37%、43%、49%、56%和62%. 蠕变- 回复试验测试系统与静态力学性能试验测试系统相同，蠕变加载时采用试验机最大许用加载速度250 N/s来加载，所有试样均在15 s之内完成加载，与图5和图6中的蠕变- 回复时间相比，加载时间足够短，可近似认为是瞬时加载。

3 试验结果分析

3.1 E-玻纤/6509环氧复合材料的吸湿性能

根据(9)式计算吸湿率，绘制复合材料在30 ℃、相对湿度80%条件下吸湿率- 时间曲线如图2所示。从图2中可以看出，吸湿曲线可以分为两部分，满足Fick第二扩散定律。在吸湿初始阶段，曲线斜率较大，且吸湿率与吸湿时间的平方根之间近似满足线性关系。这是因为Fick扩散定律描述的是浓度梯度驱动的介质扩散行为，在吸湿初期，材料内部浓度梯度较大，水分子扩散速率较大；吸湿一段时间后，材料内部浓度梯度逐渐减小，宏观上表现为吸湿曲线的斜率逐渐减小，经过足够长时间的吸湿后，吸湿曲线最终会趋于平稳，材料达到平衡吸湿状态，平衡吸湿率Mm约为0.54%. 根据(10)式求出扩散系数D为6.92×10-4mm2/h.

图2 吸湿曲线Fig.2 Moisture absorption curves

3.2 随吸湿率变化的静态力学性能

根据作者前期研究结论[26]，试样在55 ℃、95%相对湿度环境中达到饱和吸湿状态(0.8%)需要40 d以上。因此，为了排除长时间吸湿状态调节引起附加老化的影响，选定0%(干态)、0.3%(吸湿约4 d)和0.6%(吸湿约12 d)3个吸湿率，并假设试样内部的湿浓度沿厚度方向是均匀分布的，测试得到复合材料的静态力学性能如图3和图4所示，图中公式采用线性拟合方式得到，自变量x表示吸湿率，y表示弹性模量。由图3和图4可以看出，横向和面内剪切方向的力学性能均随吸湿率的增加而降低。这是因为吸湿引起基体开裂，并同时降低了纤维- 基体界面粘结强度。

图3 横向力学性能Fig.3 Mechanical properties in the transverse direction

图4 面内剪切性能Fig.4 Mechanical properties in the in-plane shear direction

单向复合材料的纵向力学性能主要受增强纤维控制，通常认为纵向力学性能不受环境因素影响。因此，只测试纵向试样的干态力学性能，得到纵向弹性模量El=41.71 GPa，纵向拉伸强度Xt=929.8 MPa.

3.3 非线性黏弹性性能

3.3.1 Schapery非线性黏弹性参数

图5和图6所示为不同应力、不同吸湿率条件下，E-玻纤/6509环氧树脂复合材料横向和面内剪切方向上的蠕变- 回复应变随时间的变化曲线。由图5和图6可以看出，两个方向上都表现出明显的黏弹性力学行为，且当横向应力超过26 MPa、面内剪切应力超过15 MPa时，两个方向上都呈现出非线性特征。另外，尽管横向和剪切方向的蠕变应变都随着吸湿率的增加而增加，但是吸湿并没有明显改变线性阈值。对于0.6%吸湿率的横向试样，由于吸湿降低了拉伸极限强度，在最大应力水平下47 min后发生蠕变断裂。

采用解析法辨识复合材料在不同应力水平下的Schapery非线性参数。其中，干态试样的非线性参数值随应力的变化规律如图7所示。图7中，g0t、g1t、g2t、aσt为横向非线性参数，g0s、g1s、g2s、aσs为剪切方向非线性参数。对于线性情况，非线性参数赋值为1. 利用Origin曲线拟合得到非线性参数随基体八面体剪应力的函数关系如表3所示。依据理论模型，利用干、湿态试样的非线性参数对比获得不同应力水平下的湿移位因子，发现湿移位因子基本不随应力发生变化，验证了构建理论模型过程中所做假设的合理性。将不同应力水平下的湿移位因子做平均化处理，结果如图8所示。对于干态试样，湿移位因子赋值为1. 通过线性拟合得到湿移位因子与吸湿率的函数关系如表4所示。从非线性参数和湿移位因子的变化规律可以看出，E-玻纤/6509环氧复合材料面内剪切方向上的非线性黏弹性比横向更为显著，也更容易受吸湿率影响。

图5 不同应力下横向蠕变- 回复应变随时间变化曲线Fig.5 Creep-recovery strain curves in the transverse direction

图6 不同应力下面内剪切蠕变- 回复应变随时间变化曲线Fig.6 Creep-recovery strain curves in the in-plane shear direction under different stresses

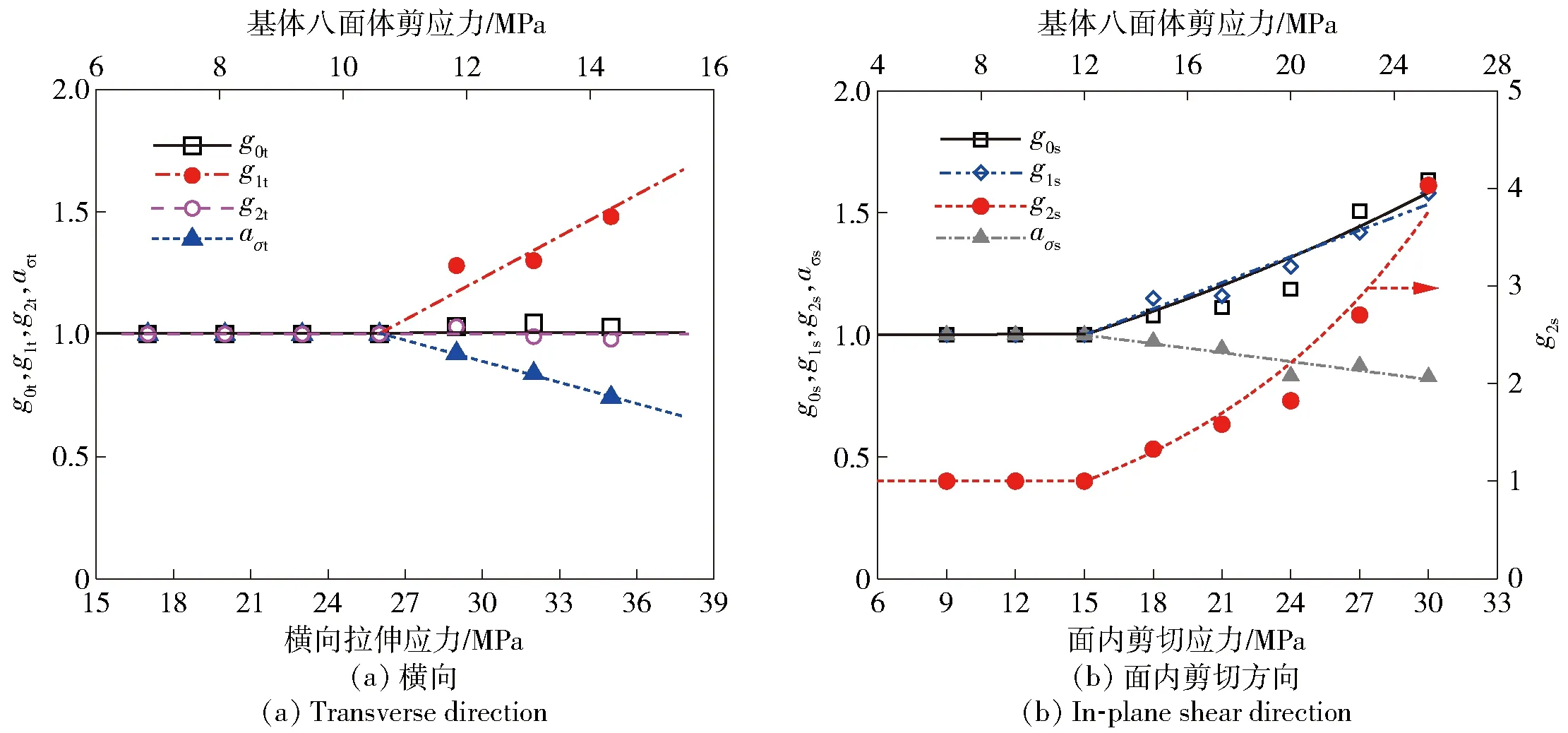
图7 E-玻纤/6509环氧复合材料非线性黏弹性参数随应力的变化规律Fig.7 Nonlinear viscoelastic parameters of unconditioned E-fiberglass/6509 epoxy composite

表3 非线性参数拟合函数Tab.3 Fitting functions of nonlinear parameters

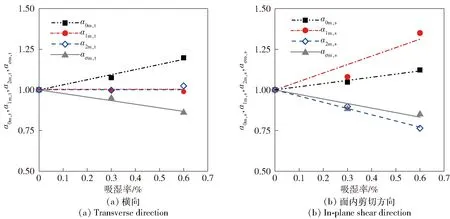
图8 湿移位因子随吸湿率的变化规律Fig.8 Moisture shift factors of the E-fiberglass/6509 epoxy composite

表4 湿移位因子拟合函数Tab.4 Fitting functions of moisture shift factors

3.3.2 线性瞬时蠕变柔量参数

根据时间- 应力等效原理(TSSP)[27]，以最低应力水平为参考，在对数时间坐标系内对短期蠕变柔量曲线移位，获得长期线性蠕变柔量主曲线如图9所示。为了验证TSSP的适用性，对E-玻纤/6509环氧树脂复合材料开展36 h的蠕变试验，采用北京钢铁设计研究总院有限公司产YYU-10/100型引伸计测量记录试样的蠕变应变。从图9中可以看出，基于TSSP获得的主曲线与试验曲线一致性较好。

由于在对数时间坐标系内很难用(3)式直接拟合主曲线，首先用指数函数在对数时间坐标系内匹配主曲线，然后用(3)式拟合相应的指数函数曲线，从而获得线性瞬时蠕变柔量参数，如表5所示。

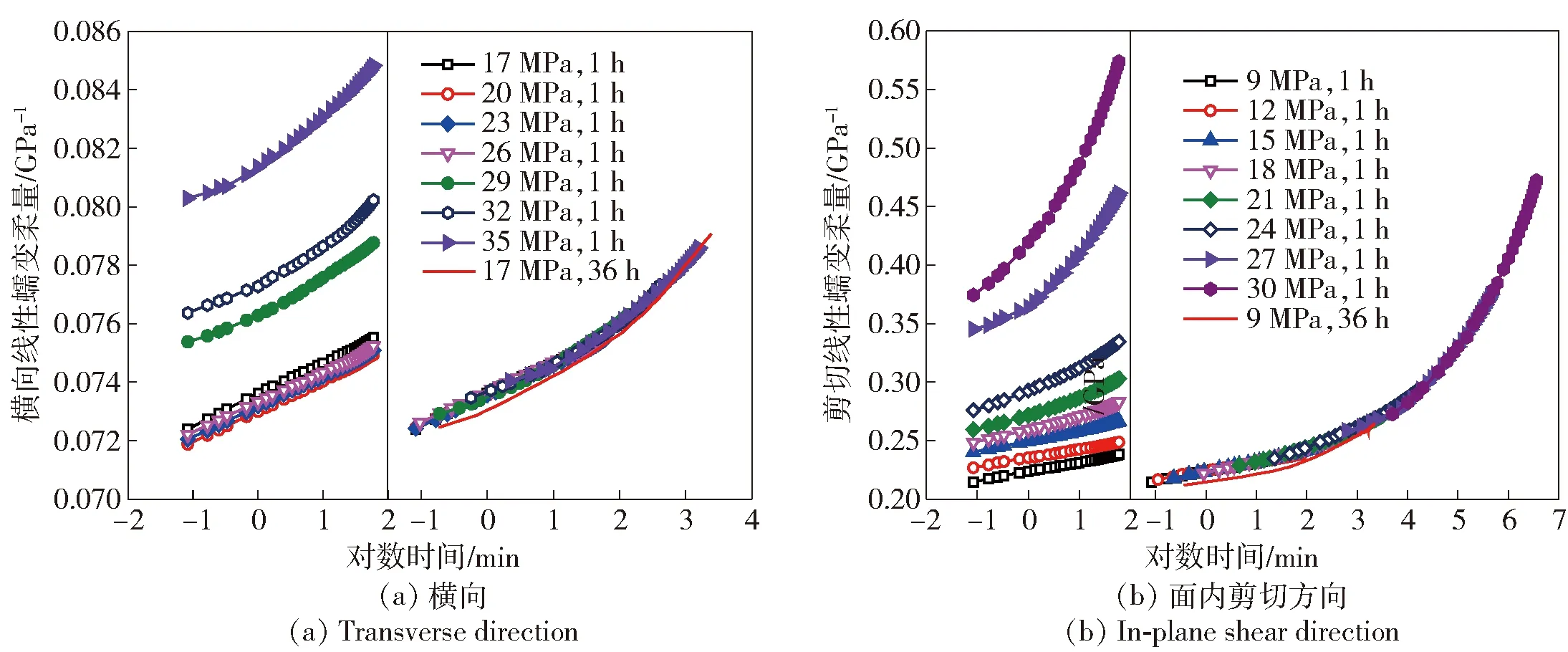
图9 不同应力和时间下线性蠕变柔量主曲线Fig.9 Master curves of linear creep compliance under different stresses at different times

表5 线性瞬时蠕变柔量参数Tab.5 Parameters of long-term linear transient creep compliance

4 定向器长期堆码贮存蠕变变形预测

4.1 有限元模型

4.1.1 网格划分

利用Abaqus软件对箱式复合材料定向器进行简化和离散建模，简化后的有限元模型主要包括箱体框架、20根复合材料定向器和20发火箭弹，用集中质量点代替不影响结构刚强度的附属机构，通过刚性单元与相近节点连接模拟真实的质量分布。箱体框架和火箭弹(包含前、中、后3个定心部)用六面体减缩积分单元(C3D8R)离散。由于需要同时模拟水分扩散过程，沿定向器壁厚方向需要包含多层网格以满足有限元计算的要求。根据复合材料定向器的实际铺层方式[90/(±53.7)5/90]，采用网格偏置方法沿定向器厚度方向创建12层网格，并赋予六面体热力耦合单元(C3D8T)，定向器的局部网格模型如图10所示。与实际结构不同的是，有限元模型中定向器本体与安装定位环分别建模，通过绑定约束。箱式定向器整体网格模型如图11所示，共包含1 505 855个网格。

图10 定向器局部网格图Fig.10 Local view of director mesh

图11 箱式定向器有限元模型Fig.11 Finite element model of box-type directors

4.1.2 分析步、材料、载荷及边界条件

1)分析步。考虑到热传递和质量扩散过程的相似性，采用Abaqus软件中的热- 力耦合分析模块模拟复合材料中的吸湿- 蠕变耦合行为。共设置3个分析步，分别用于模拟堆码加载、长期堆码贮存和移除上层两个箱式定向器的卸载过程。其中，长期堆码贮存分析步长度为15 a，控制最大增量步长度为360 h，以保证足够的计算精度。

2)材料。尽管金属材料室温下的黏弹性远不如聚合物基复合材料明显，但是在载荷的长期作用下也会出现缓慢的蠕变变形。因此，在有限元模型中考虑了金属箱体框架材料的蠕变行为，利用Abaqus软件自带的时间硬化模型赋予蠕变材料属性。作者前期针对箱体框架材料开展蠕变试验，获得了相关的材料参数[28]。复合材料定向器通过湿法缠绕成型，壁厚为3.0 mm，根据实际铺层方式，逐层对离散网格定义局部材料方向，并赋予吸湿和非线性蠕变材料属性。

3)载荷及边界条件。根据各部件之间的实际装配关系，有限元模型中采用链接单元模拟火箭弹与定向器在轴线方向上的闭锁挡弹力，火箭弹前、中、后3个定心部与定向器内表面之间定义面- 面接触关系，第1、2、3定位安装环(每根定向器共包含4个，从前端开始依次编号为1,2,3,4)与箱体框架相应位置之间定义面- 面接触关系，第4定位安装环与箱体框架相应位置设置绑定约束。箱式复合材料定向器以三层堆码的方式长期贮存，以受载最大的底层发射箱为研究对象，将上面两个发射箱的质量(约4 t)简化为均布载荷施加到箱体框架的相应位置上。对箱体底面与堆码工装接触区域施加边界条件，约束3个平动自由度U1=U2=U3=0. 另外，为了模拟吸湿过程，对定向器所有暴露表面施加归一化水分浓度边界条件。载荷及边界条件示意图如图11所示。

4.2 子程序流程

根据理论模型，采用Abaqus软件提供的子程序接口UMAT和USDFLD编写用于计算复合材料吸湿- 蠕变耦合响应的子程序，其流程图如图12所示。

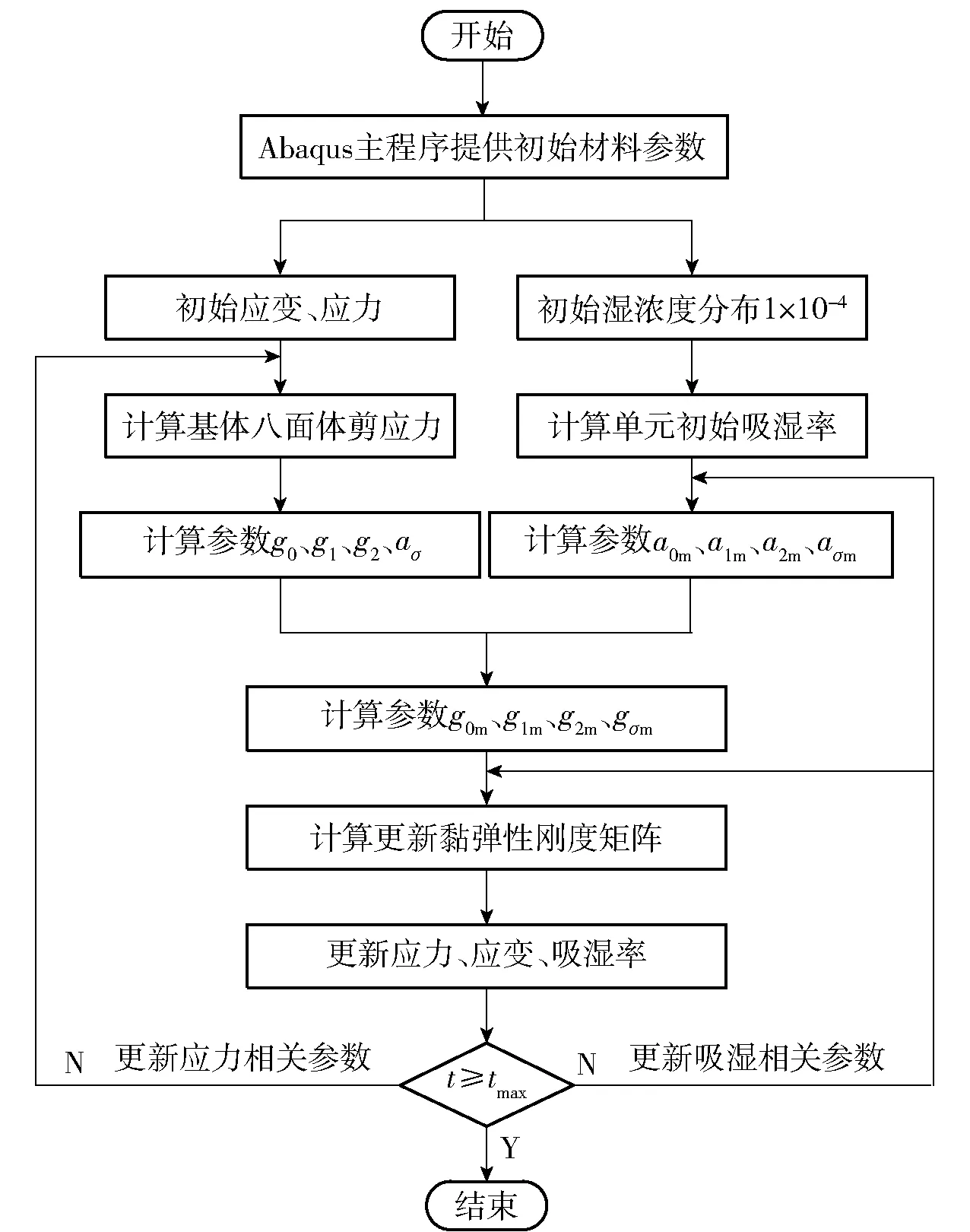
图12 程序流程图Fig.12 Program flow chart

编程总体思路如下：

步骤1利用USDFLD子程序接口将吸湿量定义为场变量。

步骤2在UMAT子程序接口中计算与应力相关的非线性参数，并计算更新与场变量相关的湿移位因子和准静态弹性模量。

步骤3新刚度矩阵，获得新的应力、应变。

步骤4循环进行步骤1～步骤3，直至达到设定的分析步时间。

4.3 结果分析

4.3.1 复合材料定向器的吸湿过程

采用归一化水分浓度对复合材料定向器中的水分分布进行无量纲描述，0表示完全干燥状态，1表示饱和吸湿状态。贮存不同时间后，定向器内部的归一化水分浓度分布如图13和图14所示。由图13和图14可以看出，贮存1 a后已经有水分存在于定向器的内表面，贮存8 a后定向器基本达到饱和吸湿，此时沿壁厚方向的水分浓度在宏观上呈现均匀分布状态。另外，从图14中可以看出，水分在定向器内部的扩散速度随着贮存时间的延长而逐渐降低，与试验曲线表现出的吸湿规律相一致。这是因为水分在复合材料内部的扩散行为主要是由浓度梯度驱动，随着定向器内、外表面浓度梯度减小，扩散速度会逐渐降低。

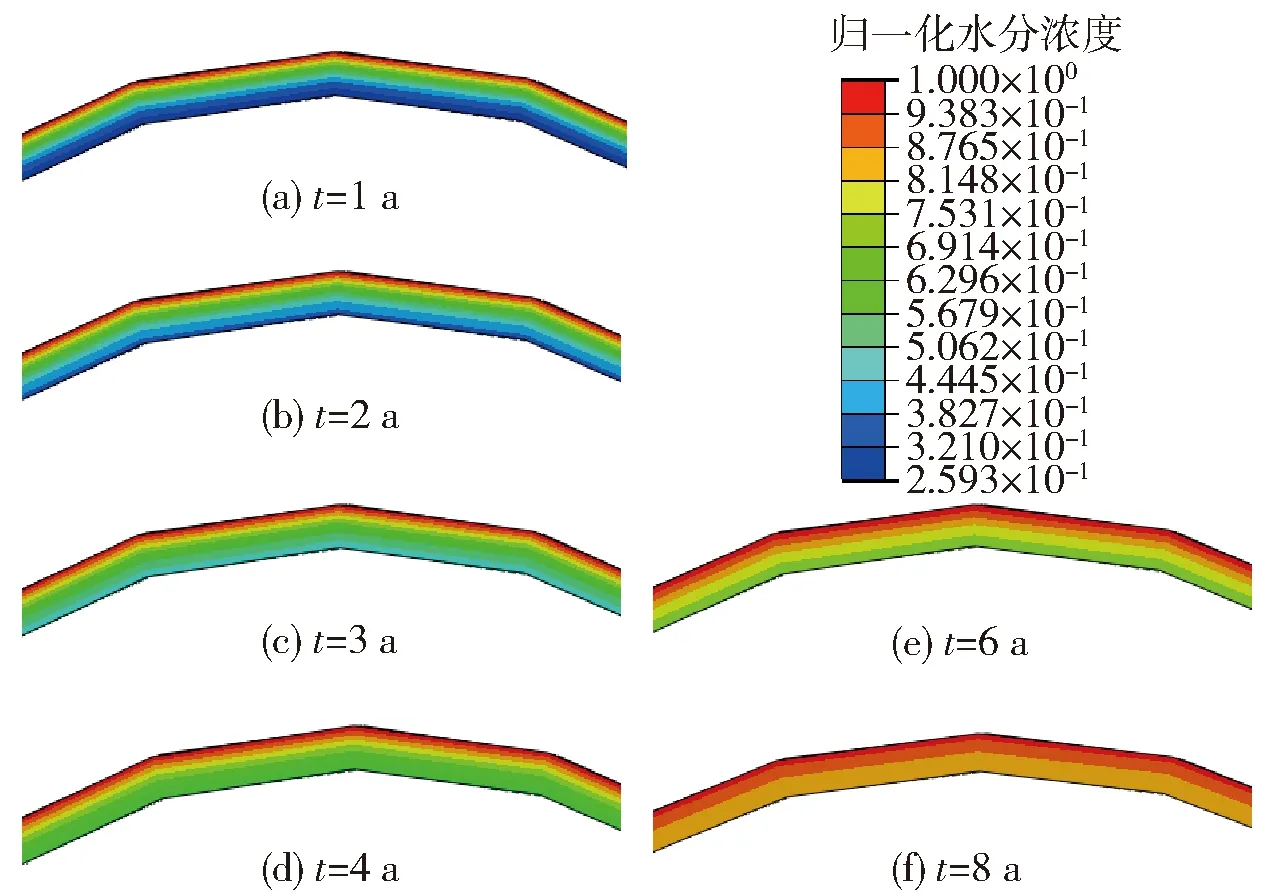
图13 不同时间后水分浓度分布云图(横截面局部)Fig.13 Moisture concentration distributions after different times of storage (local view of director)

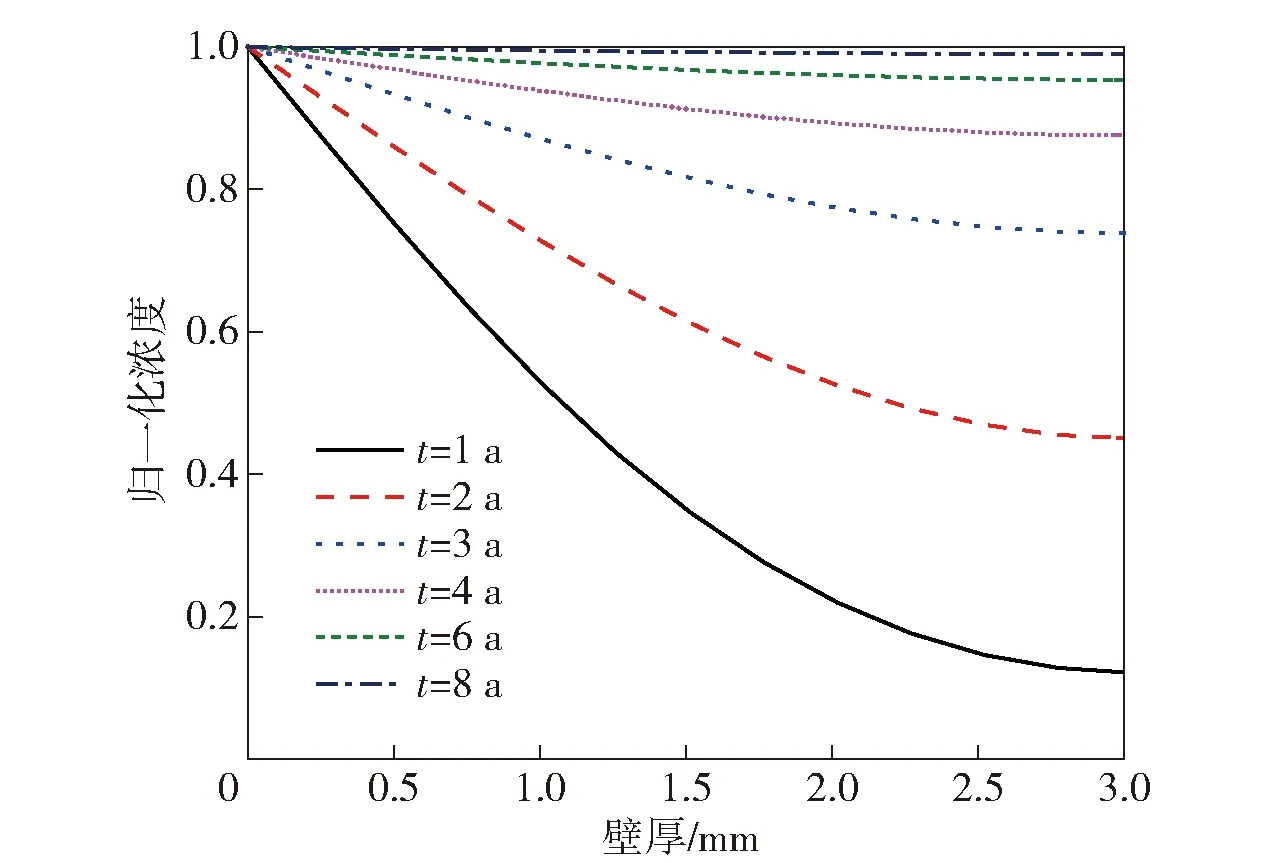
图14 不同贮存期下沿壁厚方向的水分浓度分布Fig.14 Moisture concentration distribution along the direction of wall thickness during the storage period

4.3.2 复合材料定向器的残余变形

定向器是火箭武器系统中与火箭弹直接接触的重要部件，发射时赋予火箭弹初始离轨速度和方向，而蠕变变形会引起定向器的直线度、管间平行度和箱体安装面的平面度等发生变化，直接影响火箭武器的射击密集度，甚至会导致发射安全事故。图15显示了在实际仓库环境中以3层堆码形式贮存15 a后，材料吸湿- 蠕变耦合作用引起底层箱式定向器的残余变形分布云图。由于火箭弹的质心以及前、中定心部位于第2、3安装定位环之间，该段定向器承受火箭弹的大部分质量，并且第2、3安装定位环之间的距离较大，所有20根定向器的最大变形位置都位于第2、3安装定位环之间。

图15 定向器的残余变形分布云图Fig.15 Residual deformation distribution of directors

分别提取20根定向器的最大残余变形作三维曲面图，如图16所示。由图16可以看出，定向器的最大残余变形在三维空间内近似呈现马鞍状分布，位于上、下两行中间位置定向器的残余变形最大，最大值约为0.38 mm，左右两列中间位置定向器的残余变形最小，最小值约为0.33 mm. 纵观整个箱式定向器，各定向器的最大残余变形位置、数值差异较小。

图16 定向器最大残余变形的空间分布规律Fig.16 Spatial distribution of maximum residual deformation of director

5 结论

本文推导了考虑复合材料吸湿效应的三维正交各向异性非线性蠕变本构模型，对箱式定向器采用的E-玻纤/6509环氧树脂复合材料开展了吸湿试验、静态力学性能试验和蠕变- 回复试验；通过有限元软件提供的子程序接口对本构模型进行二次开发，建立了复合材料湿扩散- 非线性蠕变耦合行为数值分析模型，预测了箱式复合材料定向器在实际仓库环境中长期堆码贮存蠕变变形规律。得出以下主要结论：

1)E-玻纤/6509环氧树脂复合材料的吸湿规律可以用Fick扩散模型描述，复合材料横向和剪切方向的弹性模量和强度随吸湿率的增加而逐渐降低。

2)当施加的横向拉伸应力超过26 MPa、面内剪切应力超过15 MPa时，E-玻纤/6509环氧树脂复合材料表现出非线性黏弹性特性；材料吸湿会导致蠕变应变增加，但是并不会明显改变线性黏弹性应力阈值。

3)以一般条件军用仓库(Ⅲ级仓库)作为箱式复合材料定向器的长期贮存场所，经过1 a时间后，水分扩散到定向器内表面，而定向器基本达到饱和吸湿状态需要8 a.

4)所有20根定向器的最大残余变形位置都位于第2、3安装定位环之间，并且在三维空间内近似呈马鞍状分布。上下两行中间位置定向器的残余变形最大，最大值为0.38 mm，左右两列中间位置定向器的残余变形最小，最小值为0.33 mm，各定向器的最大残余变形位置、数值差异较小。