浅议运输管理中表上作业法对物流管理学生能力的培养

党永龙

摘  要：运输管理中表上作业法的求解过程，有效地培养学生决策能力。文章首先介绍表上作业法的求解过程。然后采纳Excel解决以及划分问题时的使用办法和妙招，探讨了使用Excel估量决策题目时得到的结果之间的差距;再后，研讨了教育中学生学习Excel时经常或者说多频出现的错误，同时给予相应地解决方法;最后，将Excel在实际教育中的重点应用加入研讨。

关键词：表上作业法;最小元素法;Sumproduct;Excel

中图分类号：F712    文献标识码：A

Abstract： The solving process of table work method in transportation management can effectively cultivate students' decision-making ability. This paper first introduces the solving process of table operation method. Then it adopts the methods and tricks of using Excel to solve and divide problems， and discusses the gap between the results of using Excel to estimate and plan problems. Then， discusses the education of students learning Excel often or frequently errors， while giving relative solutions. Finally， the key use of Excel in practical education is discussed.

Key words： table operation method; minimum element method; Sumproduct; Excel

学生在学习运输中表上作业法时，运用最小元素法展开计算的时候频频出现问题，在开展教学活动的过程之中，进一步将Excel进行引进，并通过其进行规划求解，对学生来说有帮助同时可以很快得出结果，验证最小元素法在运行中的可行性，让计算更加的精简明了，学生对此的活跃度也会随之提升，同时在采纳Excel估量策划题目的时候，其展现规划模型的程度很理想。从教学和学生学习的层面来看，Excel在解决运输中的表格操作问题方面基本没有什么研讨。此文运用office2010 Excel解决交通问题的办法和技巧，针对性地就Excel计算规划问题过程之中结果差异的出现进行研究与分析。再次，就教学过程之中，学生使用Excel计算规划问题时出现的相关问题进行研究，并给予了与之对应的解决办法。最后研讨了引入Excel在教学中有什么重大意义。

1  表上作业法的简介

采取列表的办法求解线性规划题目中运输模型的计算办法即为表上作业法。开始初始方案，然后采取检验数开展检验当下方案，要么就得应用闭合回路法、位势法等方法开展调节，直至得到最优方案。

1.1  表上作业法步骤

步骤1：依据已知条件列出产銷平衡表和运价表。

步骤2：确定开始方案时采取最小元素法（就近供应原则）。

步骤3：通过闭合回路验证目前的方案是不是最优，假如验证数都为正实数，当下方案即为最优;只要有验证数为非正数，则得调节运量直到其为最优。

1.2  闭合回路法检验方案

所谓闭合回路，就是把一个表示非基本变量的空间（其分派量为零）的分派量调整为1。由于产销平衡的要求，必须将这个空间的闭环顶点的调度量增加或减少1。最后，我们计算这些变化给整个运输方案的总运输成本带来的变化。如果表示非基本变量的所有空间的检查数，即非基本变量的检查数，大于等于零，则得到最优解;否则，继续迭代寻找最优解。

闭合回路的特点：（1）每行每列至多有两个顶点;（2）折线必须平行或者竖直;（3）回路的转折位必须为一个基变;（4）每个非基不定量必须有同时仅仅为一条闭回路，与其方向无关。

1.3  现行方案的调整

在进行最优方案检验，如得到负检验数时，说明当下方案不为最优，此方案有必要展开修正，闭合回路是频频应用的解决办法。闭合回路的基本理解为：以空格作为转入，在有两个以上空格情况下，一般选择最小的空格号，以其对应的非基数变量作为转入变量。以转入网格为起点做一个闭环，依次标记+1和-1计算值。从封闭形道路的偶数顶点网格中选择运输量最小的数字网格作为标注网格，并以其对应的基变量作为标注变量;以闭环中最小的调度值作为调整数，调整后得到最优调度方案。

2  最小元素法在规划求解中的应用

2.1  问题提出

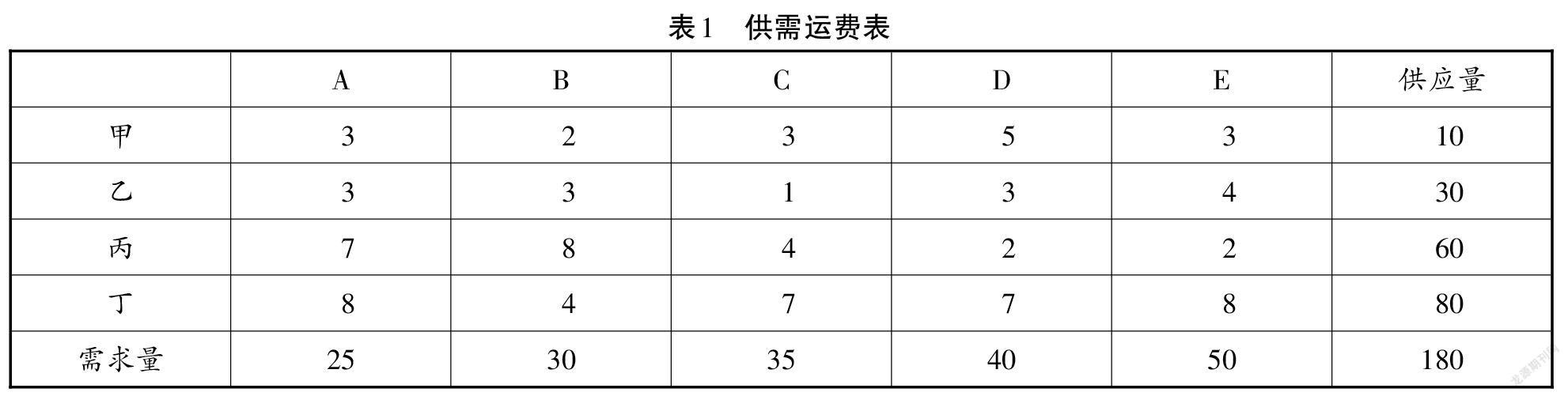
已知某厂每月可生产甲产品180吨，先运至甲、乙、丙、丁四个仓库，然后在分别供应A、B、C、D、E五个用户。已知仓库容量分别为10、30、60、80吨，各用户的需要量分别为25、30、35、40、50吨。已知从该厂经各仓库然后供应各用户的运费如表1所示，尝试找出一个让总运费最低的办法。

2.2  方案求解

利用最小元素法（就近原则）构建运输平衡中的表上作业法运输成本最低。数学模型为式（1），对于产销平衡的运输问题，总供应量等于其总需求量为公式（2）。

Z=xc                                                （1）

a=b                                                 （2）

S.T.

第一步：应用最小元素表构建运输平衡方案（就近原则），按照表2的顺序找出最小运价，完成初始方案如表3。

Z=xc=725

第二步：进行闭合回路检验（如表4）

闭合回路计算：3-2+4-8=-3。

7-2+2-8=-1。

闭合回路假如验证数都是正实数，则当下方案为最优;验证数只要有一个为非正实数，则有必要调节最终达到最优，调整量为其运量的最小值。调整新的运输方案如表5所示。

Z=xc=665

方案1与方案2相比较，节约60元，年复一年，日复一日，节约大量成本。

3  运用Excel求解运输中表上作业法

3.1  问题提出

如问题2.1。

3.2  方案求解

总成本最低，运用Excel达到最优，总成本为运量与运价的乘积。计算公式为：

Z=xc                                              （3）

第一步：在Excel表格中復制运输基本表，利用Sumproduct输入目标函数，将运量与价格相乘，点击确定，得到目标值（如图1）。

第二步：点击“文件”→点击“选项”→点击“加载项”→点击“规划求解加载项”→点击“转到”→选中“规划求解加载项”→点击确定。

加载项对话框如图2所示。

第三步：需对供应量、需求量求和，公式如下：

x=ax=ba=b                                     （4）

求和对话框如表6所示。

第四步：点击“数据”→点击 “规划求解”，输入规划求解参数，得到图3。

第五步：点击求解

规划求解结果对话框如图4所示。

输出对话框结果如表7所示。

4  高职学生在进行Excel求解运输规划问题时常见问题及改进办法

学生在运行Excel开展计算规划题目时，经常多次出现以下几方面错误：

（1）不能区分各个版本的规划求解，无法找到规划求解选项

如Microsoft Office版本，单点“文件”，单点“选项”，单点“加载项”，单点“规划求解加载项”，单点“转到”，点击“规划求解加载项”，单点“数据”，选择“线性规划”，找不到规划求解结果。如图5所示：

在WPS版本，表格中，点击“数据”，单点“模拟分析”，点击“规划求解”命令，找到规划求解功能。如图6所示：

（2）不能正确表示目标函数表达式和约束条件

在求解规划问题的过程之中，用单元格来表示规划问题中涉及的决策变量，与此同时，也通过这一方式进一步实现对目标函数和约束的左端表达式中的变量的表示。不过，在实际操作过程之中绝大多数的学生主要还是以数学表达式的方式为主，针对“规划解”尚未有效理解。通过Excel的使用，在进行规划问题解决的过程之中，约束条件中的目标函数、表达式必须用数值表示，让学生知道并理解，因为Excel只能针对数值进行计算，而不能针对带符号的表达式进行计算。

（3）不能熟练正确使用Excel中的函数Sumproduct和区分单元格的绝对引用和相对引用

学生不能正确使用Excel中的Sumproduct函数。由于每个单元格在表示表达式时使用的公式都是相似的，为了避免重新输入，需要区分单元格公式的绝对引用和相对应用。以实践训练的方式，实现数学对Sumproduct函数使用熟练度的提升，同时，要针对学生就Sumproduct的功能和使用方法进一步培训，在提升学生函数操作熟练度的同时，进一步使得其理解的深入化。有关单元格的绝对引用和相对引用的问题，能够安排学生在训练的过程之中借助某个单元格复制、粘贴方式进一步针对单元格变化进行比对。一般而言，公式是相对引用单元格的话，在向其他单元格进行复制粘贴的过程之中，公式中的单元格也会出现一定程度的变化，不过公式若是属于绝对引用的话，将会维持不变。在实践过程之中，学生能够进一步对这一特点加以发现。

（4）在进行相关设置时，不能正确反映不等式

进行规划设计时，约束条件中有出现等式与不等式两种可能。但是默认状态下，系统中是显示为“≤”，即不等式的。学生在使用时经常会忽略符号的更改，造成约束条件设置不正确。对于这一问题，按照教学经验，可以用下列办法加以解决。先是让学生了解Excel在进行规划计算时，需要对其选项进行必要的检查。接着要根据规划问题对计算问题多次重复，以养成使用前多加检查的习惯，这样一来就可以进行选项的正确设置。在学习过程中，还要鼓励學生之间多加讨论，并互为监督，跟上学习进度，互相查错，总结每次实践计算的不足之处，有利于降低错误率。

5  规划论教学中应用Excel的意义

使用Excel进行运输规划，可以帮助学生提高决策能力，解决现实中存在的运输优化问题;另外，规划问题在通过Excel进行求解时，结果显示为表格中出现的系数与不等号，从而得出规划模型。这一做法可以看作是电子表格建模。有的学生提出，在依据特定理论进行规划问题的计算时，因为涉及的计算较为复杂，对于计算结果难以做出对错与否的判断。但是如果学生熟练地掌握了Excel计算时，就能够很快地对结果进行判断，这时就可以轻松地对理论结果进行分析了。在教学中引入

Excel，提高了学生对理论的把握能力和对算法的应用能力。Excel可以对规划问题进行直接计算，而无须像理论上的标准算法那样，先得把规划问题进行标准化;而且可以快速地完成灵敏度分析，从而降低计算工作量，增强学生的学习动力。在教学过程中，让学生参与讨论，进一步对错误出现的根源进行深度挖掘，有助于学生提升实践能力、观察能力和提高学生之间的合作水平。

参考文献：

[1] 张孟飞，王铁旦，李建楠. 基于表上作业法的产销不平衡运输问题应用[J]. 价值工程，2018（23）：24-27.

[2] 张贵彬，王芸. 用表上作业法求解简单物流运输问题[J]. 中国外资，2014（6）：77-79.

[3] 李如兵，宗凤喜. 产销不平衡运输问题求解方法教学研究[J]. 曲靖师范学院学报，2015，34（3）：35-38.

[4] 李苑辉，刘李雅，芦海英，等. 高职学生科学决策能力的培养探索——以运输问题表上作业法为例[J]. 科教文汇，2017（4）：69-73.

[5] 张晓瑾，刘海生. 运输问题的表上作业法中初始方案的优化[J]. 华北科技学院学报，2014（6）：73-75，79.