疫情冲击下批发零售业SC 结构变动分析
2021-05-02张本飞
□文/ 张本飞
(乐山师范学院 四川·乐山)
[提要]本文使用18 个时期我国批发零售业增加值季度数据和CHOW检验模型对3 个可能的回归方程进行实证分析,检验我国批发和零售业增加值的SC结构变动冲击问题。当置信水平为95%时,疫情背景下我国批发和零售业增加值SC结构变动冲击不显著;在68.77%的置信水平我国批发和零售业增加值存在SC结构变动冲击;通过两个可能的回归方程残差平方和的比率构造统计量F,F 值小于显著水平为0.05 的临界值,此时我们不能拒绝使用CHOW检验模型以分析我国批发零售业增加值的SC结构冲击问题;在置信水平为89%时,F 统计量会大于临界值,即表明在分析我国批发零售业增加值的SC结构冲击问题时不能直接使用CHOW检验模型。
2020 新年以来,新冠肺炎疫情席卷全球,该疫情对我国批发零售业产生了较大的负面影响。在2020 年第一季度,我国第三产业增加值为123,008.5 亿元,同比下降3.7517%,其中批发零售业增加值为18,703.7 亿元,同比下降14.6382%;从2020 年第二季度开始,我国服务业明显好转,第三产业增加值为135,418.9 亿元,同比增加3.2636%,其中批发零售业增加值为23,641.6 亿元,同比增长2.5528%;2020 年第三季度第三产业增加值为142,821.7 亿元,同比增加5.9310%,其中批发零售业增加值为25,061.6 亿元,同比增长4.6540%;2020 年第四季度第三产业增加值为152,727.6 亿元,同比增加7.8558%,其中批发零售业增加值为28,279 亿元,同比增长5.7570%。为检验2020 年我国批发零售业是否存在统计学意义上的SC 结构变动,拟在下文结合国家统计局相关数据进行详细实证分析。
一、相关数据及数据处理
为了检验2020 年我国批发零售业是否存在统计学意义上的SC结构变动,我们对国家统计局官网中批发零售业增加值2016~2020 年季度数据进行处理,相关数据见表1。表中第五栏的指标“占比”表示该季度批发和零售业增加值在当季度GDP 中的所占百分比。(表1)
二、相关统计方法
2020 年新冠肺炎疫情对我国服务业增加值产生冲击,属于服务业增加值之中批发零售业增加值也受到疫情冲击,为了检验疫情对我国批发和零售业增加值的SC 结构变动冲击是否在统计学意义上显著的问题我们进行CHOW Test 统计检验(下文中简称CHOW 检验)。
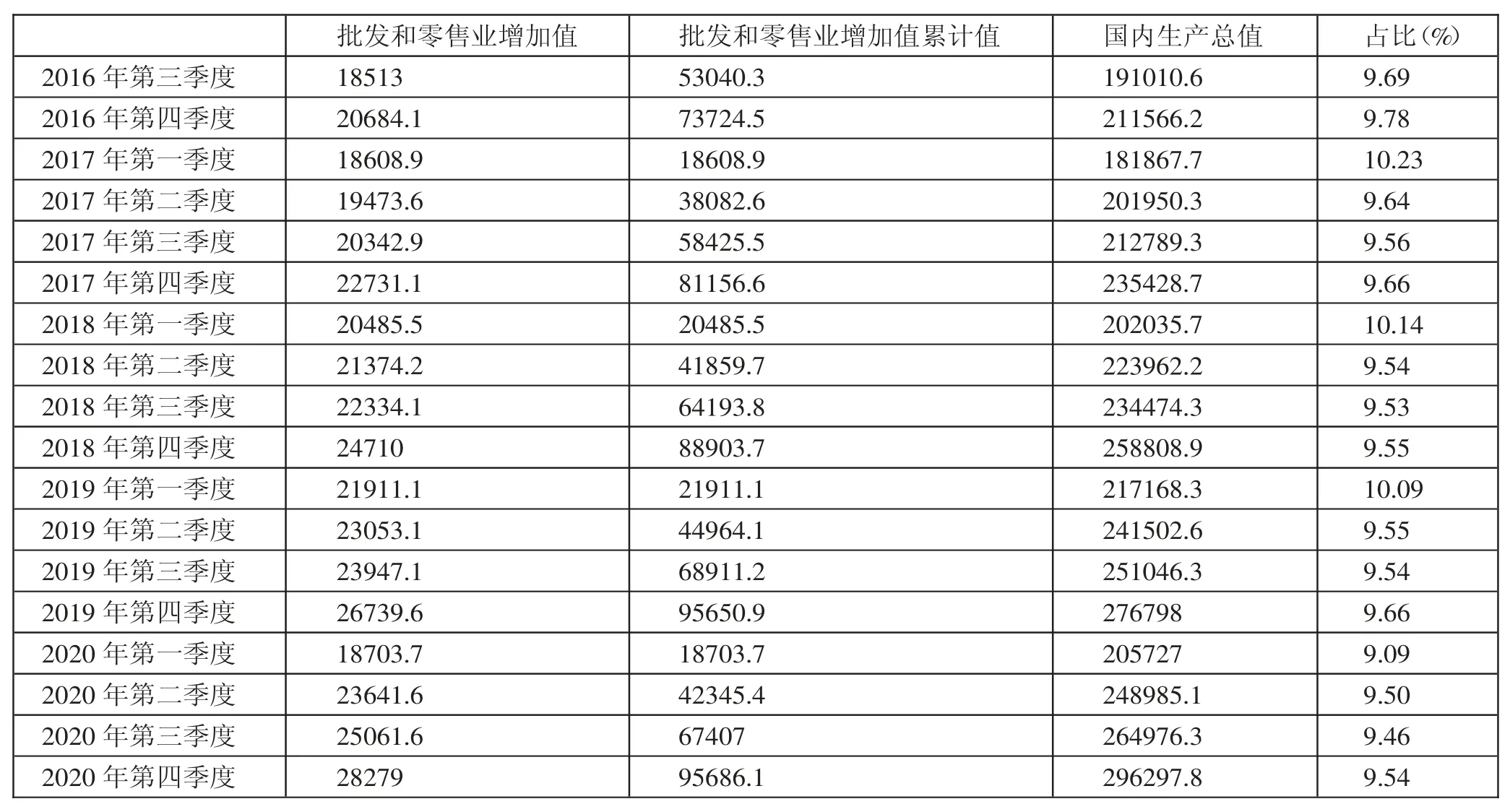
表1 批发和零售业相关数据分季度统计数据一览表(单位:亿元)
根据表1 中历年各季度GDP 和批发零售业增加值相关数据所作的描述统计分析我们可知,在置信度为0.95 时,批发零售业增加值在GDP 中的占比区间稳定在(0.09594,0.09888);在置信度为0.997 时,批发零售业增加值在GDP 中的占比区间稳定在(0.09497,0.09985)。在没有SC 结构变动冲击时批发零售业增加值在GDP 中的占比稳定在9%~10%之间。按照凯恩斯消费函数,GDP 的增加可以导致消费增加。当疫情来袭时,批发和零售业增加值SC 结构冲击会导致主要解释变量的解释力度出现较大结构变动。根据CHOW 检验我们可以列出如下3个可能的回归方程。
包含10 个时期的2016 年第三季度至2018 年第四季度可能的回归方程1 如下:
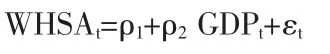
包含8 个时期的2019 年第一季度至2020 年第四季度可能的回归方程2 如下:
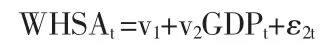
包含18 个时期的2016 年第三季度至2020 年第四季度可能的回归方程3 如下:
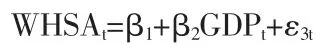
回归方程1~3 中WHSAt表示第t 期的我国批发和零售业增加值,GDPt表示第t 期的我国GDP(注:此处数据均为季度数据而非年度数据),如果回归得到的系数在三个回归模型中保持统计学意义上的不变,即当ρ1=v1=β1,则不存在我国批发和零售业增加值的SC 结构变动冲击。
三、CHOW 检验回归模型分析
根据上文CHOW 检验所列出3 个可能的回归方程和18 个时期我国批发和零售业增加值相关数据,我们将回归结果整理为表2。根据CHOW 检验基本原理,我们需计算F 统计量检验我国批发和零售业增加值的SC 结构变动冲击。
F=16(RSSR-RSSUR)/2RSSUR 样本统计量服从于自由度为2 和14 的F 分布,其中回归方程1~3 中约束残差平方和RSSR=4 300299;方程1~3 中无约束残差平方和RSSUR=1216503+2425048=3641551。F=14×(4300299-3641551)/(2×3641551),F=1.2663,所以p=FDIST(F,2,14),p=0.3123。选择显著水平a=0.05,即置信水平=1-a=0.95。我们在95%的置信水平不能拒绝原假设ρ1=v1=β1,即在统计学意义上我国批发和零售业增加值SC 结构变动冲击不显著;选择显著水平a=0.3123,即置信水平=1-a=0.6877。我们在68.77%的置信水平拒绝原假设ρ1=v1=β1,即我国批发和零售业增加值存在SC 结构变动冲击。(表2)
四、CHOW 检验误差方差分析
上文中CHOW 检验模型暗含的基本假定是回归方程1 和回归方程2 的误差方差相同;对此问题我们可以通过F 分布检验这两个误差方差是否相同。如果两个回归方程误差方差相同,即表明我们可以直接使用CHOW 检验分析我国批发零售业增加值的SC 结构冲击问题,否则我们需要修正CHOW 检验模型进行分析。
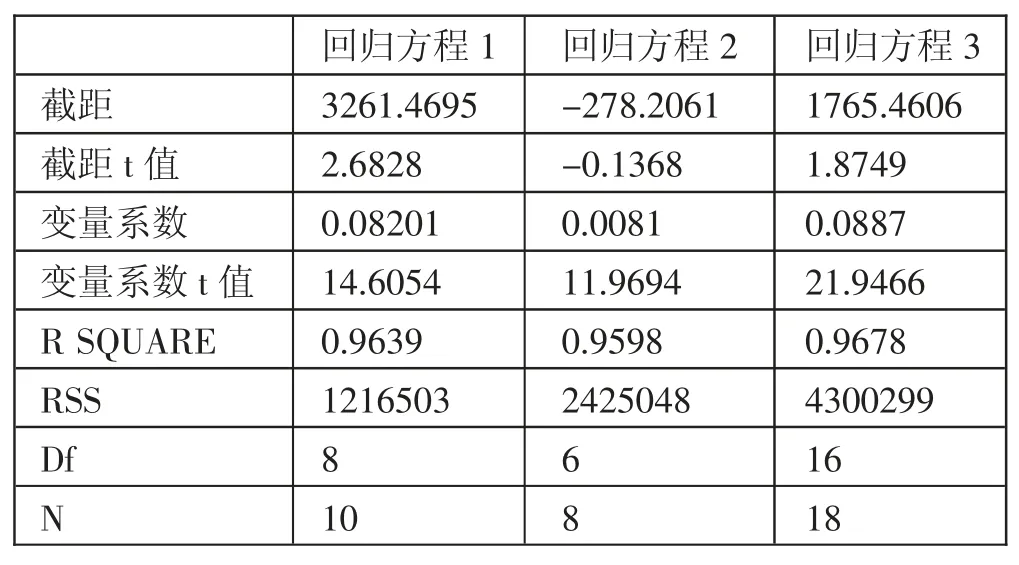
表2 批发和零售业增加值SC冲击分析一览表
我们通过回归方程1 和回归方程2 回归结果中的RSS 来计算两个回归方程的误差方差估计值。回归方程1 的观测次数为10,回归方程1 的误差方差1 估计值=RSS1/(10-2),其中RSS1=1216503,所以误差方差1 估计值为=1216503/8;回归方程2 的观测次数为8,回归方程2 的误差方差2 估计值=RSS2/(8-2),其中RSS2=2425048,所以误差方差2 估计值为=2425048/6。在两个回归模型总体方差相等的虚拟假设下我们可以通过两个误差方差估计值之比构建F 统计量,因为回归方程2 的误差方差2 估计值大于回归方程1 的误差方差1 估计值,按照较大的方差估计值置于分子的基本原理,我们的统计量F=(2425048/6)/(1216503/8),即F=2.6579443。分子分母自由度分别为6 和10,且显著水平为0.05(即置信水平为0.95)的临界值为FINV(0.05,6,8)=3.5805803,由于统计量F 值小于显著水平为0.05 的临界值,我们不能拒绝两个回归模型总体方差相等的虚拟假设,即此时我们不能拒绝使用上文中CHOW 检验模型以分析我国批发零和售业增加值的SC 结构冲击问题;由于p 值=FDIST(F,6,8),即p 值为0.1008582,在置信水平为89%时,F 统计量会大于临界值,我们拒绝两个回归模型总体方差相等的虚拟假设,即表明我们在分析我国批发和零售业增加值的SC结构冲击问题时不能直接使用CHOW 检验模型,而必须对CHOW 检验模型进行修正后才能更为有效地分析我国批发零售业增加值的SC结构冲击问题。
五、结语
本文使用我国批发和零售业增加值季度数据和CHOW 检验对3个可能的回归方程进行实证分析,以检验我国批发和零售业增加值的SC 结构变动冲击问题,在95%的置信水平我国批发和零售业增加值SC 结构变动冲击不显著;在68.77%的置信水平我国批发和零售业增加值存在SC 结构变动冲击。我们使用两个可能的回归方程残差平方和的比率以构造统计量F,来判断CHOW 检验模型在分析我国批发和零售业增加值的SC 结构冲击问题时是否需要修正。由于统计量F 值小于显著水平为0.05 的临界值,我们不能拒绝两个回归模型总体方差相等的虚拟假设,我们无需修正CHOW 检验模型以分析我国批发零售业增加值的SC 结构冲击问题;在置信水平为89%时,F 统计量会大于临界值,我们拒绝两个回归模型总体方差相等的虚拟假设,即在置信水平为89%条件下分析我国批发零售业增加值的SC 结构冲击问题时不能直接使用CHOW 检验模型,而必须对CHOW 检验模型进行修正后才能更为有效地分析我国批发零售业增加值的SC 结构冲击问题。
主要参考文献:
[1]贾俊平.统计学[M].北京:中国人民大学出版社,2019.
[2]古扎拉蒂.计量经济学基础[M].北京:中国人民大学出版社,2011.
[3]杨维忠.SPSS 统计分析与行业应用案例详解[M].北京:清华大学出版社,2019.
[4]薛薇.基于SPSS 的数据分析[M].北京:中国人民大学出版社,2019.
[5]曹宝明,冯睿,刘婷.互联网有助于降低交易成本吗?——以粮食批发价格为例[J].调研世界,2021(02).
[6]赵宇辉.力促国内网络零售业蓬勃发展 [N].中国财经报,2021-02-25(005).
[7]牛亮.数字经济新业态促进下的零售业态模式创新——基于组织韧性视角[J].商业经济研究,2021(04).
[8]赵娴,王丹莹.智能化驱动下零售业转型与发展路径研究[J].中国市场,2021(06).
[9]徐佳敏.“内循环”利好零售业,“用工难”成行业难题[J].人力资源,2021(03).
[10]余远坤.数字化下零售业的发展路径研究 [J].现代商业,2021(03).
