本征光学中弯曲情况下光纤温度测量传感器的应用

孙俊峰，赵 吉，吴明岳，贺会超

（吉林省计量科学研究院，吉林 长春 130103）

由于光纤很容易达到弯曲效果，因此，许多实验室已经研究了曲率对光纤测量响应的影响。在光纤中实现的光栅可提供测量，还研究了与弯曲有关的性能。因此，功率衰减系数弯曲光纤的长度是将光纤用作换能器必须确定的参数之一。在作者先前的论文中，描述了一种确定局部数值孔径和几何形状的几何方法，其可以仅在制造过程中在接近玻璃的温度下弯曲光波导时应用融化。在这种情况下，纤芯和包层的折射指数受温度影响独立修改曲率半径，本文描述了一组使用平面光波导作为通过弯曲测量温度换能器的方法，其中仅涉及一些透射光强度影响。目的是扩展分析平面光波导在光纤测量温度中的应用。

1 弯曲光纤中的光传播

弯曲光纤中的光传播阶跃折射率和光纤纤芯中的光路是笔直的，但几何形状的描述更为复杂。在弯曲的平面波导中，沿着给定的光路，光线在外部纤芯-包层界面上的入射角保持相同，并且对于所有的光路都适用。然而，在弯曲的光纤中，仅在包含该弯曲部分的子午平面内进入光纤弯曲部分的光线起作用。对于进入该平面的偏斜光线，由于光纤弯曲导致的不对称性，纤芯内的后续反射不会遵循简单的可重复模式。射线不变量的复杂形式和描述射线路径的微分方程式无法简化。因此，我们提出了一种数值技术，用于沿着弯曲的光纤分别跟踪每条光线。

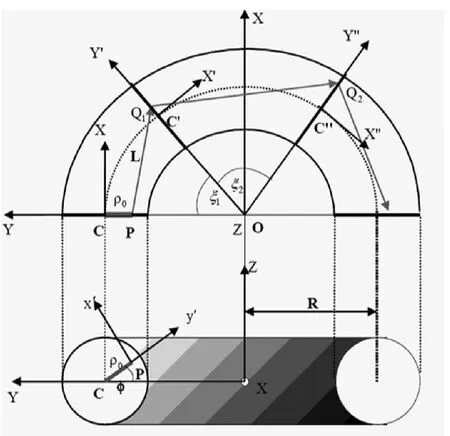
图1 光纤截面的示意图，该光纤的曲率遵循半径为R 的弧线

在图1 中，考虑了任意入射光线进入在弯曲部分开始处的点“P”处X'X 截面（ξ=0）。光纤的弯曲部分通过圆形横截面绕原点“O”以半径R 的旋转而形成圆环部分。轴系统OXYZ 的轴OX 直接指向纸张。局部坐标系ox'y'z'和oz'指向纸张，也以P 表示。入射到“P”的任意射线的方向余弦相对到ox'y'z'。

向量OP 由下式给出：

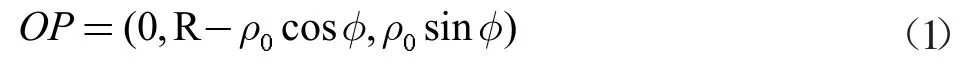
如果让r 为沿P 远离光线的点“L”，则点P 与纤维中心的距离为p，那么：

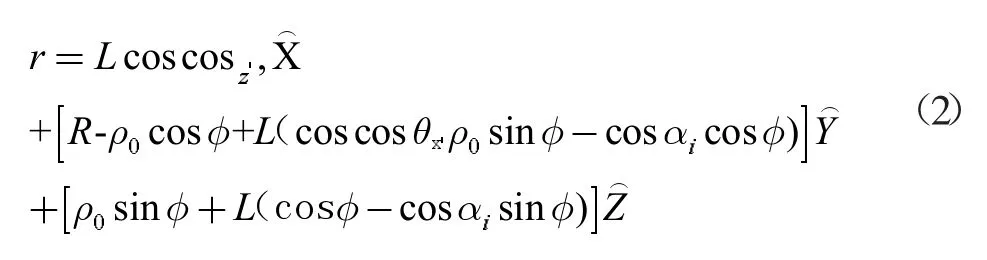
如果光线在“Q1”处遇到圆环，则可以写，其中“Q1”是第一个反射的位置。在“Q1”，我们有：

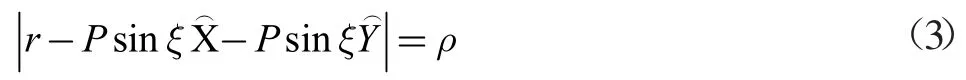
这给出了围绕弯曲的光纤曲率轴的角距离ξ：

ξ1对应于POQ。从等式（6），推导出一个方程，该方程将根据位置“L”提供具有弯曲的光纤纤芯-覆层界面的光线的截面。等式的最小实数正解表示距离“L1”。

从光纤圆环上第一个反射“Q1”的点开始，光线被反射到弯头周围圆环表面（纤芯-包层界面）上的另一个点。

在第一次反射之后，给出到下一次反射的距离“L”的所有解作为三次问题的解。为了获得三次方程，我们必须在二次方程式中ρ0替换为ρ。

确定了射线路径的几何形状之后，我们可以使用以下公式计算沿给定路径的每个折反射点的分数功率损耗：

其中γ 是每条光线的衰减系数，沿着弯曲的光纤从一次反射到下一次反射变化，由下式给出：

其中△ξ 是两次连续反射之间的角度间隔，而N 是反射的总数。然后，可以使用广义菲涅耳定律来计算沿给定路径的每个反射点处的透射系数Ti。

给出了折射光线（V垲1）的透射系数的代数表达式：

但是有些光线以接近θc的入射角到达界面最后，在光学器件弯曲部分角长度“ξ”末端的总强度通过四重求和找到波导式（7）在X'X 处的光纤横截面积（r，准）和射线角（θ，ψ）的分布的关系式：

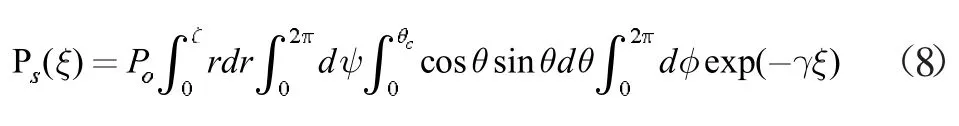
在图2 中绘制了阶跃折射率光纤的归一化功率衰减量与沿着弯曲光纤轴的归一化距离（z/ρ）的关系。其中“z”是曲率长度（z=R·ξ）。每条曲线显示相同的特征。最初，存在过渡区域，其功率损耗很快。该区域以折射系数最大的折射射线和隧道射线为主。光纤弯曲部分的行为类似于平面波导弯曲部分，但是过渡区域中的功率损耗并不那么重要，因为只有很少的光线靠近子午平面时损耗较大。

2 光纤温度测量原理

光纤传感器是一种固有的光纤传感器。敏感元件是光纤的弯曲部分（图3）。该传感器原理基于传感光纤输出光强度随光纤温度变化而变化。由光纤弯曲效应引起的光能损失将通过热效应进行动态补偿。因此，仅通过温度变化来调制输出信号强度。

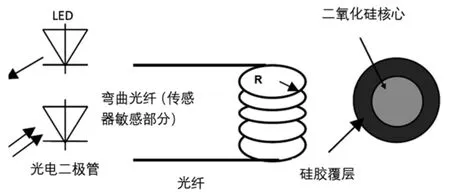
图3 温度传感器原理图

3 温度对弯曲光纤内部局部数字孔径的影响

对于给定的光纤曲率半径（R=R0），按以下方式写出光纤根据温度的弯曲部分内侧的局部数值孔径：

其中，根据温度（T）以以下方式写入芯折射率和包层折射率：

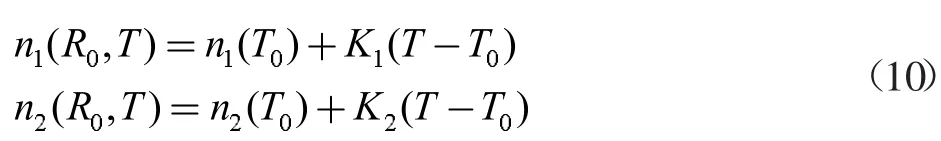
系数K1=dn1/dT 和K2=dn2/dT 分别是纤芯的热光系数和折射率的包层的热光系数。

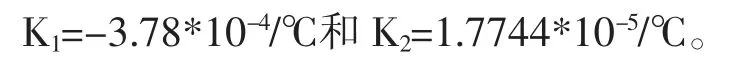
有机硅基的泊松剂使它们非常适合光学应用。出色的热稳定性（-115°C 至260°C）使该材料可用于高温传感应用。

在这种光纤中，通过使用构成包层的聚合物的负热光学系数抵消了用作芯的无机玻璃波导中小的正热光学系数效应。

对于施加的温度T，根据“ρ0”的值绘制光纤中的局部数值孔径。我们观察到，当施加的温度增加时，局部数值孔径增加。因此，在室温下未被引导的光线在大于T0的温度下被引导。

4 温度变化对弯曲光纤中光传播的影响

在本节中，分析了温度变化对弯曲光纤中光传播的影响。曲率半径对光纤温度响应的影响，为了进行该分析，给出了曲率半径R 和光纤弯曲部分的长度（ξ）。纤芯和光纤包层的折射率取决于温度。几何模型用于根据温度评估光输出功率。接收处输出功率换能器的光纤弯曲部分的末端由下式给出：

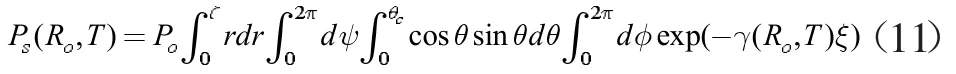
对于给定的曲率长度（ξ=2πR0），在图4 中绘制了传感器在多个R0值下对温度变化的归一化输出的光强度响应。在图4 中提出的用作温度传感器的光纤响应曲线类似于平面波导温度传感器。对于第一种方法，没有考虑过测量错误。当局部数字孔径响应于隧道效应引起损耗恢复而达到饱和时，传输速率（P/P0）会增加。可以说，温度感应范围取决于光纤的曲率半径。

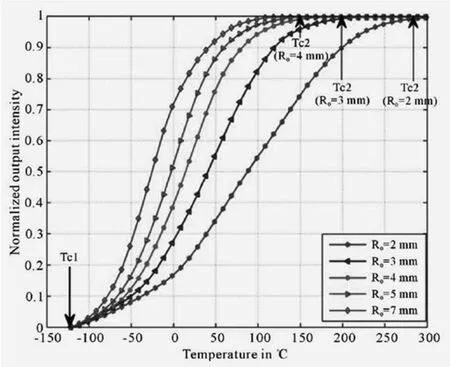
图4 各种曲率半径下根据温度的透射率

可以从图4 推断出：

Tc1和T0之间的响应曲线部分对应于仅由温度效应引起的强度损失。

T0和Tc2之间的响应曲线部分对应于仅由光纤曲率引起的强度损失。

当弯曲光纤的曲率半径减小时，光纤温度传感器响应的线性区域增大。传感器灵敏度由下式给出：

其中P（R0，T）是输出强度。从图4 得出，温度传感器的灵敏度与曲率半径成反比。

5 结束语

文章分析了温度变化对弯曲光纤曲率半径不同的多模光纤弯曲光功率损耗的响应。已经发现，当光纤弯曲角度增加，由于内部光纤数的孔径变化引起的弯曲损失增加。更为重要的损耗是由折射和隧道效应引起的。已经证明弯曲的光纤可用作温度传感器。在使用过程中弯曲光纤。其在高温下的制造可以最大程度地减少一些残留的机械效应，并可以严格使用几何方法来描述光的传播，评估光功率输出值的损失并校准温度传感器。如果使用例如二氧化硅、硅酮纤维作为换能器，则可以获得良好的性能，并具有出色的灵敏度和线性度到较大的温度测量范围，主要是因为对有机硅的热光效应值是负的且重要的。