带双时间窗约束的粮食专用车调度优化

唐丽敏　张雅茹　潘相君　张殿勇

摘要：

针对港口企业经营的粮食专用车调度问题，在传统的车辆调度问题上新增双时间窗约束，以粮食专用车周转率最大和港口企业经营粮食专用车的收入最大为目标建立双目标规划模型，并用算例验证模型和算法的有效性。结论如下：在运量与运距相矛盾的情况下，优先选择距离近、运量小的客户进行服务。此研究能够为粮食专用车调度决策提供参考。

关键词：

粮食专用车; 双时间窗; 优化模型; Gurobi求解

中图分类号：  U294.1+2; U294.8+91

文献标志码：  A

Scheduling optimization of special vehicles for grain

with double time window constraint

TANG Limin1， ZHANG Yaru1， PAN Xiangjun1， ZHANG Dianyong2

（1. College of Transportation Engineering， Dalian Maritime University， Dalian 116026， Liaoning， China;

2. Yantai Port Co.， Ltd.， Yantai 264000， Shandong， China）

Abstract：

Aiming at the scheduling problem of special vehicles for grain operated by port enterprises， the double time window constraint is added to the traditional vehicle scheduling problem， and the two-objective programming model is established with the objectives of the maximum turnover rate of special vehicles for grain and the maximum income brought by port enterprises to operate special vehicles for grain. The validity of the model and the algorithm is verified by examples. The conclusion is as follows： in the case of contradiction between transportation volume and transportation distance， customers with close distance and small transportation volume are preferred to serve. This research can provide reference for the scheduling decision of special vehicles for grain.

Key words：

special vehicle for grain; double time window; optimization model; Gurobi solving

收稿日期： 2020-06-08

修回日期： 2020-09-22

作者簡介：

唐丽敏（1963—），女，辽宁大连人，教授，博士，研究方向为交通运输工程，（E-mail）tlmin@dlmu.edu.cn

0 引 言

“北粮南运”是我国粮食物流的主要特征。为促进散粮高效运输，粮食码头或粮食物流企业备有铁路粮食专用车（以下简称“粮食专用车”）。粮食专用车的调度受到铁路和货主时间的限制，若在此双时间窗约束下实现对粮食专用车的合理调度，对提高粮食专用车周转率具有重要意义。

车辆调度的核心问题是车辆路径问题（vehicle routing problem，VRP）。1959年DANTZIG等[1]首次提出VRP，并给出一个基于线性规划的近似最优解的求解方法。很多学者为更快捷地得出较为精确的车辆调度方案，根据不同场景做了一系列研究，具体表现在对各种启发式算法的改进上：QIU等[2]面对分散的客户需求，提出具有特殊设计的数学模型和禁忌搜索算法，并通过对比证明该方法的优越性;LIAO等[3]在调度作业中加入对时间序列加权时滞的考虑，提出一种单机环境下具有竞争性的蚁群优化算法;胡云清[4]设计了适用于VRP求解的模拟退火算法，并提高了该算法的求解性能;李秀娟等[5]根据物流车辆调度系统自身和蚁群算法的特点，对蚁群算法进行了改进。随着研究的进一步深入，一些学者开始研究带时间窗的车辆路径问题[6]（vehicle routing problem with time windows ，VRPTW），如韩广等[7]针对VRPTW提出一种改进的粒子群优化算法，解决了普通粒子群优化算法收敛慢和精确度低的问题。部分学者结合多目标模型研究VRPTW：郭小乐等[8]针对高铁站公交时刻表与车辆调度综合问题，建立多目标综合优化模型，并设计遗传算法求解;庞燕等[9]建立了车辆最少和路程最短的双目标模型，并改进了两阶段禁忌搜索算法;范厚明等[10]为提高种群的多样性，设计了适合求解多目标VRP的混合遗传算法。铁路方面的车辆调度研究主要是从降低成本和提高客户满意度（即减少等待时间）等方面进行的，如任苹等[11]建立了多种旅客列车期望时间和运行时间最短的多目标模型，运用集成粒子群优化算法解决优化调度问题。

综上，既有文献对带时间窗的车辆调度模型和算法做了很多改进，但很少将其直接运用在铁路上[12]。文献[13]成为仅有的将车辆调度运用到粮食专用车上的文献。与道路车辆调度问题不同的是，港口或粮食物流企业拥有的粮食专用车在利用铁路进行粮食运输时，面临来自客户和铁路两方面的时间窗约束，加上铁路运输在一定时间内的容量限制，仅凭经验进行粮食专用车的调度，不仅达不到粮食专用车的高效周转，而且可能增加额外成本。因此，粮食专用车调度问题具有硬时间窗限制的特殊之处。

为解决粮食专用车调度问题，本文考慮铁路规定的硬时间窗和客户所规定的软时间窗的双重约束，建立混合整数规划模型。该模型以港口经营粮食专用车的收入最高和粮食专用车平均运行时间最短为目标，并考虑同一铁路线同一时间段所容纳车皮组数和同一车皮组前后服务时间的约束。设置“粮食专用车平均运行时间最短”的目的是让粮食专用车在周期内运转次数最多，即周转率最高。

1 问题描述

已知粮食专用车的类型、客户与港口之间的距离、客户所需运输的货量、铁路规定的港口与客户间线路的硬时间窗、客户的软时间窗、随运输距离发生变化的运价等，为得到每一车皮组服务客户的选择以及服务的顺序，以港口经营粮食专用车的收入最高和粮食专用车平均运行时间最短为双目标，以加权的方式将双目标转化为求单目标的最大值，对双时间窗约束的粮食专用车车辆调度进行优化，确定哪组车皮为哪家客户服务，以及服务顺序、去程时间段和返程时间段。

本文提到的一个车皮组指的是一组车皮（也称一列车皮），例如

车皮组A1指的是车型为A的第1组车皮;车皮数指的是一个车皮组中车皮的数量，例如车皮组A1的车皮数为40指的是车型为A的第1组车皮共有40节车皮;车皮组数指的是车皮组的数量。

本文提到的铁路规定的硬时间窗限制是港口粮食专用车服务某个客户的去程和返程所经过铁路线的时间窗限制，这个时间窗限制是必须满足的。客户j的第t个和第r个时间段是指在一定周期内，港口与客户之间铁路线开放的第t个和第r个时间段，其中t是粮食专用车从港口去往客户j选择的时间段，r是粮食专用车从客户j返回港口选择的时间段。每个客户选择的每个铁路开放时间段都是独立的，不受其他客户所选择的铁路开放时间段的影响，例如：客户1选择的第一个铁路开放时间段可以晚于客户2选择的第二个铁路开放时间段。

图1是粮食专用车服务客户的往返示意图，包括去程和返程。

图2是模拟一个车皮组为客户服务的状态，同一车皮组在一个时间段内只能为一位客户服务，而且同一车皮组必须在一位客户处装车完毕返回港口并卸车完毕后才能为另外一位客户

服务。假设该车皮组选择客户1的第t个时间段从港口出发，到达客户1所在地并装载完毕后，选择客户1的第r（r>t）个时间段返回港口;若卸车后客户2有需求，则该车皮组重新出发，为客户2提供服务。在此过程中，每次去程和返程均必须严格满足港口与此客户之间铁路线的时间段限制，也就是说即使车皮已经全部装车完毕或者全部卸车完毕也必须等到此线路的硬时间窗开启才能出发。

2 模型设计

2.1 模型假设与符号定义

通过调查，对模型作如下假设：①粮食专用车每节车皮的最大装载量为60 t;

②对于拥有粮食专用车的港口来说，向客户收取的租车费用按每节车皮的最大装载量计算;

③铁路给出的时间窗均大于粮食专用车从港口到客户（或从客户返回港口）所需的时间;

④根据铁路线的规定，同一时间在同一条线路（从港口至同一个目的地的线路视为一条线路）上的车皮组数有一定限制;

⑤以30 d（即720 h）为一个决策周期;

⑥不考虑固定成本、折旧成本和装卸时间;

⑦每段通行均在给出的时间段的开始时刻出发，若在一个时间段的中间某时刻装车完毕或者卸车完毕，则必须等待下一个时间段开始才能出发;

⑧每个客户在其软时间窗开启之前都已经备好货;

⑨根据实际的客户需求将列车车型

分为A、B、C等3种，这3种车型的车皮数分别为[30，40]、[40，50]、[50，60]。

定义模型参数如下：R为港口经营粮食专用车获得的收入;T为粮食专用车运行时间;O为港口集合，o∈O;K为车型集合，k∈K;I为车皮组的编号集合，i∈I;J为客户集合，j∈J;ki为车型为k的第i个车皮组;Nki为车型为k的第i个车皮组的车皮数;Doj为粮食专用车从港口o到客户j的运行时间;qj为客户j的货量;Voj为粮食专用车从港口o到客户j的运价（越远越低）;[Bj，Ej]为客户j允许服务的时间窗;[bojm，eojm]为港口o与客户j之间铁路开放的第m个时间窗，m∈M;t和r分别为粮食专用车从港口到客户和从客户到港口选择的客户铁路线的时间窗编号， t，r∈M;Cki为车型为k的第i个车皮组的装卸车费用;hj为与客户j软时间窗相关的惩罚系数。

定义决策变量为：xkij，若车型为k的第i个车皮组为客户j服务，则xkij=1，否则xkij=0;ykiojt，若车型为k的第i个车皮组从港口o出发为客户j服务，并选择客户j铁路线的第t个硬时间窗，则ykiojt=1，否则ykiojt=0;wkijor，若车型为k的第i个车皮组从客户j返回港口o，并选择客户j铁路线的第r个时间窗，则wkijor=1，否则wkijor=0。

2.2 模型建立

所考虑的问题可以用两个混合整数规划模型描述，其目标分别是使港口经营粮食专用车的收入最高和粮食专用车平均运行时间最短。模型如下：

式（1）～（16）中各参数下标的范围如下：

i，i′∈I，i≠i′; k，k′∈K，k≠k′; j，j′∈J，j≠j′

t′，t∈M，t≠t′;r，r′∈M，r≠r′;r≥t+1

式（1）表示模型目标为港口经营粮食专用车的收入最高，收入包括粮食专用车出租费用和装卸费用，但要减去因开始为客户服务的时间晚于客户规定的时间而产生的惩罚费用;式（2）表示模型目标为粮食专用车平均运行时间最短，平均运行时间最短是为了使周转率最高。平均运行时间等于所有的车皮组服务客户所花费的总时间与所服务的客户总数的商，总时间包括往返路上耗费的时间和在客户处停留的时间;式（3）表示每个客户至少被服务一次;式（4）表示在不浪费资源的条件下，每一车皮组至少为一位客户服务;式（5）和（6）表示车型为k的第i个车皮组为客户j服务，去程和返程时间均需满足客户j的时间窗约束;式（7）和（8）表示在同一时间段内港口与某一客户之间铁路线上的车皮组数应小于铁路线的最大承受能力;式（9）表示在某一车皮组为某一客户服务的过程中，车皮组从港口出发在客户的某一时间段到达客户所在地，就必须在此客户的另一时间段从客户处出发返回港口;式（10）表示在客户j的时间段顺序中，上一车皮组为其服务返回港口之后下一车皮组才能出发;式（11）表示在时间顺序中，某一车皮组如果之前为某一客户服务，就必须在从此客户处返回港口之后才能再次出发为同一客户或其他客户服务;式（12）表示某一车皮组同一时间只能服务一位客户;式（13）表示为某一客户服务的车皮组数的限制;式（14）～（16）表示决策变量的限制。

2.3 模型的改进

为便于求解，对模型进行改进[14]，步骤如下：

步骤1

求解各个单目标条件下的最优值。f1、f2均用C#调用Gurobi求解，f1在本模型中为式（1），f2在本模型中为式（2）。

步骤2 将多目标转化为单目标求解。由于模型中两个目标的量纲不一致，所以需要对其进行标准化处理。令标准化函数F1=f1/f″1，F2=f2/f″2，其中f″1、f″2分别为f1、f2的最大值，此时F1、F2的值域均为[0，1]。

步骤3

用线性加权和法求权重[12]。令F=α1F1-α2F2，其中α1、α2由下列方程组确定：

因此，新目标函数为

3 算例分析

3.1 应用数据

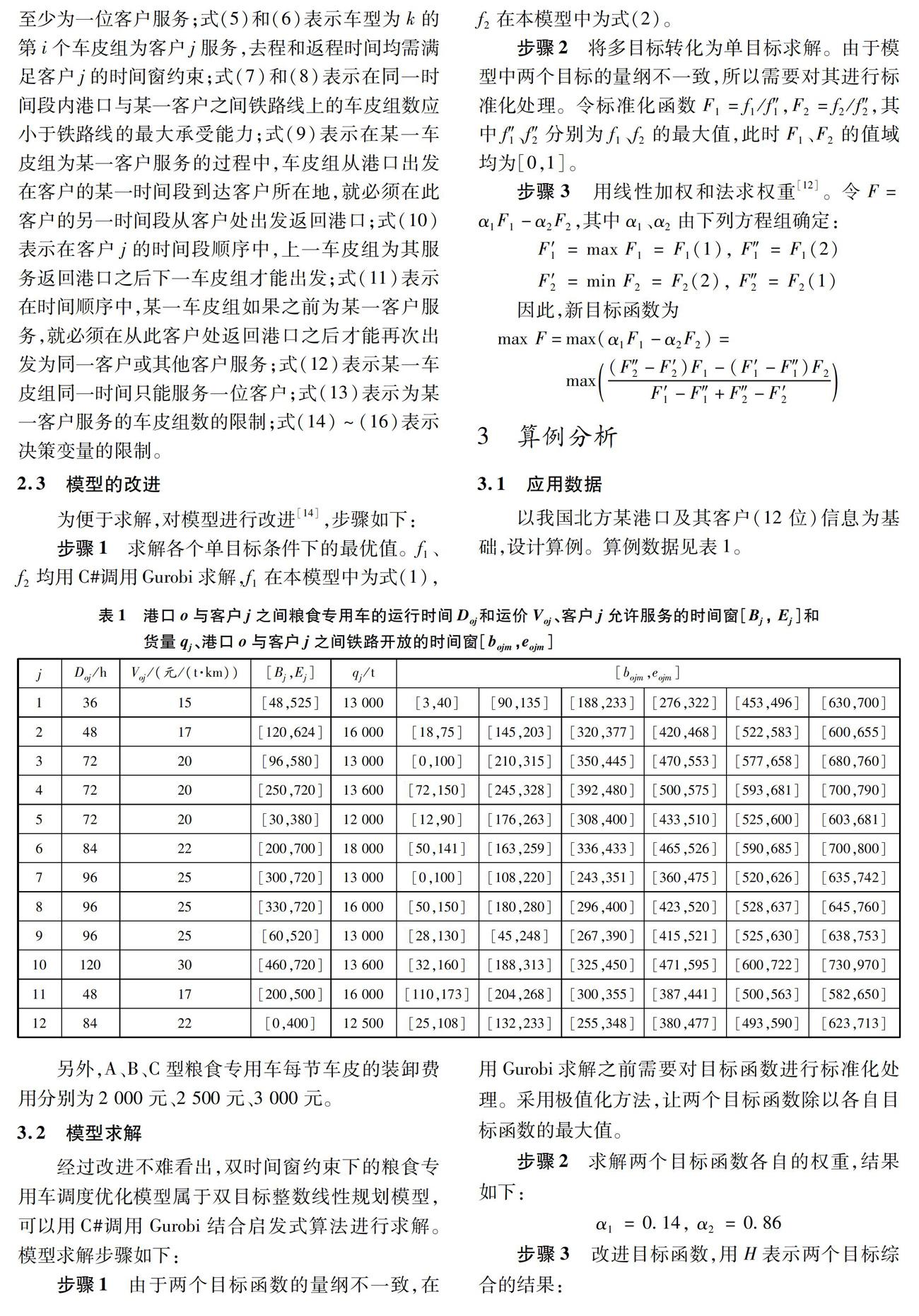
以我国北方某港口及其客户（12位）信息为基础，设计算例。算例数据见表1。

另外，A、B、C型粮食专用车每节车皮的装卸费用分别为2 000元、2 500元、3 000元。

3.2 模型求解

经过改进不难看出，双时间窗约束下的粮食专用车调度优化模型属于双目标整数线性规划模型，可以用C#调用Gurobi结合启发式算法进行求解。模型求解步骤如下：

步骤1

由于两个目标函数的量纲不一致，在

用Gurobi求解之前需要对目标函数进行标准化处理。采用极值化方法，让两个目标函数除以各自目标函数的最大值。

步骤2

求解两个目标函数各自的权重，结果如下：

α1=0.14， α2=0.86

步骤3

改进目标函数，用H表示两个目标综合的结果：

Hmax=0.14Rmax-0.86Tminj i k xkij

步骤4

利用C#调用Gurobi进行求解，输出的最终结果为8 071 133.92。这个数据表示的是一个综合的结果——在粮食专用车周转率最高的情况下使得港口经营粮食专用车的收入最高。

3.3 结果分析

为便于分析，将模型求解结果列于表2中。由表2可知，无论是哪个车皮组，均先服务完一个客户后再服务另外一个客户，服务过程遵循港口与客户之间铁路线的硬时间窗要求。

以粮食专用车第1次为客户1服务为例解读表2：客户1第一次被车型为A的第4个车皮组服务，所选择的去程和返程硬时间窗编号分别为1和2。对照表1可知，粮食专用车从港口到客户1选择的时间窗为[3，40]，从客户1到港口的返程时间窗为[90，135]。

本文使用同样的方法，单独求解标准化函数F2的最小值，将求得的车辆调度方案代入标准化函数F1进行求解，将两个结果分别乘以对应的权重，求得的结果为433 004.06;另外，单独求解标准化函数F1的最大值，将求得的车辆调度方案代入标准化函数F2进行求解，将两个结果分别乘以对应的权重，求得的结果为8 075 533.10。经过对比可知，本文使用的模型求解结果更优。另外，粮食专用车“成列”发车点集中在规模较大的十幾个站点，本文调用Gurobi求得最终的运行时间为1 100 s，能够应对实际运行的要求。

结果表明，运用优化模型进行粮食专用车调度能够使港口收入明显增加，并提高粮食专用车的周转率。

通过算例分析，还能得到3点启示：

（1）粮食专用车所挂车皮数影响粮食专用车周转率和港口的收入。本文的算例求解结果显示，相对于所挂车皮数为40节的粮食专用车来说，所挂车皮数为50节和60节的粮食专用车服务客户的频率更高。这表明在客户有足够运量需求的情况下港口应在不超过最大限制的前提下，尽可能多挂车皮。

（2）港口与客户的距离和客户运量需求对于粮食专用车服务客户的顺序有直接影响，这也决定了粮食专用车调度方案的形式。通过算例可以看出，所挂车皮数为40节的第4个车皮组先为距离573 km、运量需求为13 000 t的客户1服务，再为距离为1 449 km、运量需求为13 600 t的客户10服务。在时间窗限制下，当面对距离近、运量小和距离远、运量大的客户时，

粮食专用车会优先服务距离近的客户，这样可以有效增加一定周期内港口的收入，并且能提高粮食专用车的服务效率。

（3）所挂车皮数较少的粮食专用车会在最后进行调配，起补充作用。通过算例结果可以看出，受运费和资源的影响，为顾客提供最后一次服务的粮食专用车所挂车皮数大多为40节。

4 结 论

粮食专用车在铁路粮食运输的过程中发挥着重要作用，结合当前我国北方某港口现状，本文提出以港口

经营

粮食专用车的收入最高和粮食专用车周转率最高为目标的带时间窗的车辆调度问题，建立了混合整数规划模型，并用C#调用Gurobi求解算例。结果表明，本文所构建的混合整数规划模型是可行且有效的。

从本文的粮食专用车调度方案看，在客户运量需求较大的情况下，较为理想的是每列粮食专用车按照最大许可数量拖挂车皮。同时，面对运距不同、运量需求不同的客户，应在满足客户和铁路时间窗的情况下，尽量先考虑运距再考虑运量。另外，在求解方面，针对目前“北粮南运”粮食专用车的发车频率和规模，调用Gurobi运用启发式算法求解可以达到优化车辆调度的目的。下一步将尝试考虑大范围、多品种大宗物资的铁路专用车调运问题，使模型和算法更具普遍性。

参考文献：

[1]DANTZIG G B，RAMSER J H . The truck dispatching problem[J]. Management Science， 1959， 6（1）： 80-91. DOI： 10.1287/mnsc.6.1.80.

[2]QIU Meng，FU Zhuo， EGLESE R，et al. A tabu search algorithm for the vehicle routing problem with discrete split deliveries and pickups[J]. Computers & Operations Research， 2018， 100： 102-116. DOI： 10.1016/j.cor.2018.07.021.

[3]LIAO C J，JUAN H C. An ant colony optimization for single-machine tardiness scheduling with sequence-dependent setups[J]. Computers and Operations Research， 2007， 34： 1899-1909. DOI： 10.1016/j.cor.2005.07.020.

[4]胡云清. 求解VRP问题的混沌模拟退火萤火虫算法[J]. 包装工程， 2017， 38（7）： 216-221. DOI： 10.19554/j.cnki.1001-3563.2017.07.048.

[5]李秀娟， 杨玥， 蒋金叶， 等. 蚁群优化算法在物流车辆调度系统中的应用[J]. 计算机应用， 2013， 33（10）： 2822-2826. DOI： 10.11772/j.issn.1001-9081.2013.10.2822.

[6]CHU J C，YAN Shangyao， HUANG H J. A multi-trip split-delivery vehicle routing problem with time windows for inventory replenishment under stochastic travel times[J]. Networks & Spatial Economics， 2017， 17（1）： 41-68. DOI： 10.1007/s11067-015-9317-3.

[7]韩广， 李雪杨， 孙晓云， 等. 铁路行车调度问题的改进粒子群优化研究[J]. 控制工程， 2017， 24（9）： 1855-1859. DOI： 10.14107/j.cnki.kzgc.b1.0277.

[8]郭小乐， 宋瑞， 何世伟， 等. 高铁车站接运公交时刻表与车辆调度综合优化[J]. 铁道学报， 2019， 41（1）： 26-34. DOI： 10.3969/j.issn.1001-8360.2019.01.003.

[9]庞燕， 罗华丽， 夏扬坤. 基于禁忌搜索算法的废弃家具回收车辆路径优化[J]. 计算机集成制造系统， 2020， 26（5）： 1425-1433. DOI： 10.13196/j.cims.2020.05.026.

[10]范厚明， 吴嘉鑫， 耿静， 等. 模糊需求与时间窗的车辆路径问题及混合遗传算法求解[J]. 系统管理学报， 2020， 29（1）： 107-118. DOI： 10.3969/j.issn.1005-2542.2020.01.012.

[11]任蘋， 李楠， 高立群. 基于集成粒子群优化的复线旅客列车优化调度[J]. 系统仿真学报， 2007， 19（7）： 1449-1452. DOI： 10.3969/j.issn.1004-731X.2007.07.011.

[12]曾庆成， 于婷. 基于码头集卡共享的运输任务分配优化模型[J]. 上海海事大学学报， 2020， 41（1）： 64-70. DOI： 10.13340/j.jsmu.2020.01.011.

[13]姜世臣. 大连港散粮码头公司粮食专用车调度优化研究[D]. 大连： 大连海事大学， 2017.

[14]辛晓刚， 王彪， 李昕， 等. 考虑风电消纳能力的含风电场电力系统多目标优化调度研究[J]. 可再生能源， 2016， 34（1）： 49-55. DOI： 10.13941/j.cnki.21-1469/tk.2016.01.008.

（编辑 贾裙平）