二次谐波加权重构的77 GHz FMCW雷达心率监测方法

郑春弟，李 刚，陈荟慧，王爱国

(1.佛山科学技术学院 电子信息工程学院，广东 佛山 528225；2.清华大学 电子工程系，北京 100084)

心率是衡量人体健康状况的关键生理参数，其在临床诊断、治疗效果与健康状态评估等方面具有指标意义[1-2]。传统上，常用接触式传感器进行心率监测。但在实际使用中，接触式监测技术需要佩戴或系缚相关设备，极易引起人体的不适，特别是导联电极贴片式监测技术，长时间监测会妨碍人体其他活动，进而造成生理与心理上的抵触[3]，不利于24小时动态心电图监测的顺利执行。因此，随着人们对美好生活需求的日益增长，传统接触式心率监测技术已无法满足人们对智能化、无感化、舒适化健康监测设备的强烈需求。

与需要系缚的接触式传感器相比，心率监测雷达以电磁波为媒介，通过测量由心脏跳动引发的胸壁微小位移，能以非侵入、非接触的方式获取心脏跳动的频率，可提供舒适感极高、用户友好的心率监测方案，因此雷达技术有望成为最有应用潜力的心率监测技术[3]。虽然雷达测量心率具有非侵入、非接触、全天时的天然优势，但心率监测雷达发展也面临着一系列挑战性问题。特别地，胸壁位移由呼吸和心跳两种叠加机械运动引起，这两种运动的雷达回波信号在时域和频域上相互叠加，而且心跳的位移幅度(0.01～0.5 mm)远低于呼吸的位移幅度(约1～12 mm)[4]。因此，如何在呼吸(频率约0.1～0.6 Hz)及其谐波强干扰条件下，测量心跳的频率(频率约0.8～2.5 Hz)是心率监测雷达面临的最大挑战之一[5-6]。

基于77 GHz调频连续波(FMCW)雷达的心率监测技术是近几年新涌现的生命体征监测技术[4，7-9]。总体而言，现有的77 GHz毫米波雷达心率监测技术，在处理呼吸及其谐波强干扰下的心率估计问题时，采用的方法主要有三类，即带通滤波法[8]、最优频率估计法[4]和多分辨率分析(MRA)法[7]。尽管通过设置合适的低端截止频率，这些方法能够将呼吸的基频及二次谐波或者仅基频滤除掉(具体情况取决于呼吸频率的大小)。但是这些方法在滤波之后得到的信号并不是干净的心跳信号，其中依然可能保留着呼吸的三次或者二、三次谐波，这些残存的呼吸高次谐波将严重制约着心率估计的准确性。

针对呼吸及其谐波强干扰下的心率估计问题，提出了一种基于心跳二次谐波信号加权重构的心率估计方法，在77 GHz FMCW雷达上实现了心率的精准监测。由于心跳二次谐波所在频带远高于呼吸及其二、三次谐波的频带，因此在信号重构时仅使用心跳二次谐波所在频带的信号，可容易地剔除呼吸及其二、三次谐波的干扰[10]。为了获取较为干净的心跳二次谐波信号，提出方法使用多分辨率分析对胸壁运动信号进行多频带分解。提出方法与文献[7]中基于多分辨率分析的77 GHz雷达心率估计方法相比，最主要区别有以下两点：① 在多分辨率分析基础上，提出方法进一步将能量信息运用到心跳二次谐波信号的重构之中，而文献[7]中的方法并未使用各频带能量所蕴含的信息。具体而言，提出方法依据能量大小对各频带进行加权重构，这非常有助于凸显心跳二次谐波最可能出现的频率范围。② 提出方法是基于心跳二次谐波进行心率估计的，而文献[7]是基于心跳基频进行心率估计的。相比于心跳二次谐波的强度，处在心跳二次谐波范围的呼吸谐波、呼吸心跳交调谐波的强度几乎可以忽略[10]，因此基于心跳二次谐波进行心率估计，不仅可以避免呼吸及其谐波的强干扰，而且还可避免后续谱峰估计中模型阶数选择难题。

1 系统模型

简单的毫米波FMCW心率监测雷达发射与接收主要模块如图1所示。

图1 毫米波FMCW心率监测雷达发射与接收示意图

呼吸和心跳会引发胸壁机械运动，该运动将对照射的雷达波产生调制作用。首先通过对回波进行相应的解调，得到拍频信号，然后通过适当的信号处理，雷达能够恢复出胸壁机械运动的相关信息，进而提取出心率。

假设胸壁与雷达接收天线之间的距离为d0、发射线性调频(Chirp)信号的调频率为K、最大波长为λmax，则解调之后接收机正交和同相两个通道上的拍频信号可以表示为[4，11]

(1)

(2)

其中，Ab为拍频信号的幅度，fb为拍频，4πd0/λmax代表着胸壁径向距离产生的常数相位，4πx(t)/λmax代表着由于胸壁运动引发的相位变化情况。x(t)=xh(t)+xr(t)，为心跳xh(t)和呼吸xr(t)叠加引发的胸壁准周期机械运动信号。通常，正交与同相两路信号可以用复信号形式表示为

C(t)=I(t)+jQ(t)。

(3)

由于复信号C(t)的相位中蕴含着胸壁运动信息，因此在提取相位信息的基础上，通过慢时间维一系列合适的信号处理方法，可估计出心跳的频率。

由式(1)和式(2)可知，相位4πx(t)/λmax的大小与波长有关，即波长越短(工作频率越高)，则胸壁运动引发的相位调制量越大[4，11]。例如，与24 GHz雷达相比，在同样的胸壁运动幅度下，77 GHz雷达引发的相位调制量大约是前者的3.21倍，即77 GHz雷达的相位功率比24 GHz雷达大约高10 dB。与其他低频段的心率监测雷达相比，除了有利于信噪比的提升之外，使用77 GHz频段雷达还具有以下两个优势：① 77 GHz雷达已成为工业和汽车雷达的主流产品，大规模的商业应用有助于以极低的硬件成本实现心率监测；② 该频段可用的带宽大，非常有利于设计功能强大的心率监测雷达系统。鉴于以上优势，文中选用77 GHz频段雷达作为心率监测传感器。

2 利用心跳二次谐波信号加权重构的心率估计方法

提出的心率估计方法流程如图2所示。该方法主要包含3步：第1步是在估计胸壁位置的基础上，对信号进行预处理以滤除杂波与噪声等，从而得到较为干净的胸壁运动信号；第2步是心跳二次谐波信号加权重构；第3步是基于多重信号分类(MUSIC)算法的频率估计。下面分别对其进行说明。

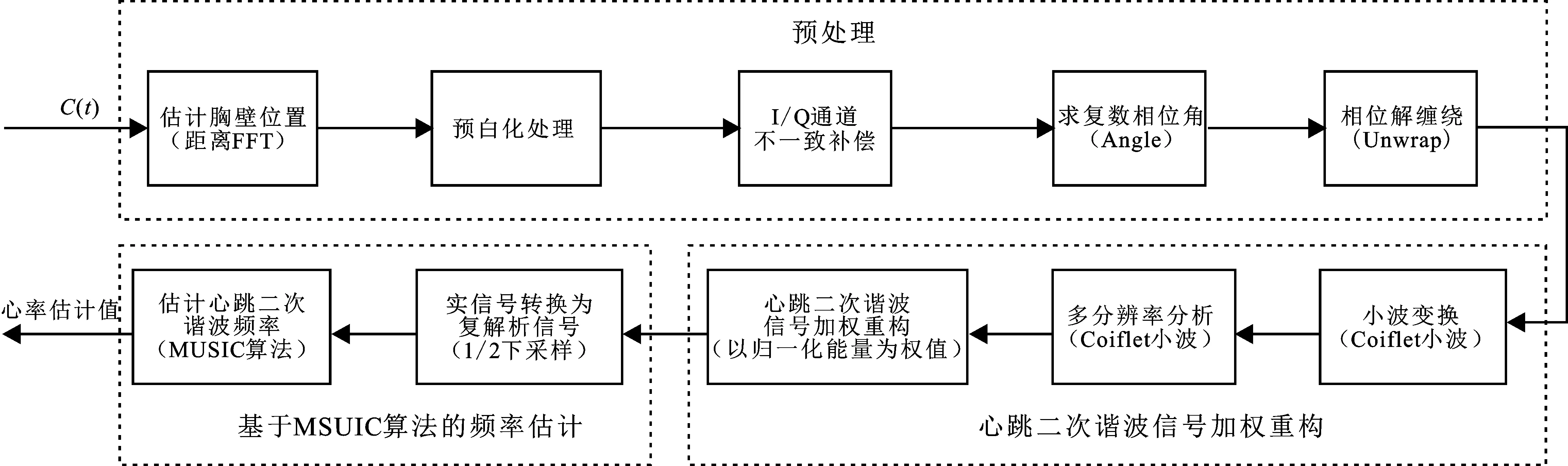
图2 基于心跳二次谐波信号加权重构的心率估计方法流程图

2.1 预处理

2.1.1 胸壁位置估计

首先对时间窗内的复信号C(t)逐Chirp求快速傅里叶变换(FFT)得到距离像，然后利用文献[12]中的标准差法计算每个距离单元的信号能量，最后将标准差最大行作为该时间窗内胸壁所在的距离单元。

2.1.2 预白化处理

在获得胸壁所在距离单元的基础上，对时间窗内信号的实部与虚部进行联合预白化处理，以降低噪声对后续相位估计的影响。

2.1.3 信号补偿

在进行心率监测时，雷达元器件中的电路非理想等不利因素，会给I/Q通道引入幅度误差、增益误差和相位偏移等[11]。由于求取相位是一个高度的非线性过程，上述这些误差极有可能导致较大的相位估计误差，因此在进行信号相位提取之前，需要进行补偿。文中采用文献[13]中的方法进行I/Q通道不一致补偿。

2.1.4 相位估计及解缠绕

在信号补偿之后，使用四象限反正切法提取信号的相位信息。当慢时间维的采样率设置合理时，相邻两次采样获取的相位应处在[-π，π]之内。但是当胸壁位移x(t)>λmax/4时，导致相位可能不落在[-π，π]之内，因此需要相位解缠绕处理。即当慢时间维相邻两次采样的相位跃变超过π时，则需要通过加减2π的倍数来更正相位。之后再进行线性去势操作，消除传感器数据偏移对后续处理的影响，以便于将分析集中在相位本身的波动上。

2.2 心跳二次谐波信号的加权重构

将经过预处理获得的相位信号记为φ(t)，首先使用Coiflet小波对其进行最大重叠离散小波变换，小波的消失矩阶数选为5，层数为7，将得到的系数矩阵记为W∈(L+1)×M，其中W的第k行表示尺度为2k的小波系数，L代表层数，M代表慢时间的采样数。然后再次使用消失矩阶数为5的Coiflet小波对W进行多分辨率分析，得到矩阵WMRA。

根据多分辨率分析的含义可知：

(4)

其中行向量φ∈1×M表示时间窗内φ(t)的M个采样组成的相位信号，表示WMRA的第k行。不妨假设心跳二次谐波所处的频率区间[1.6 Hz，5.0 Hz]大致与WMRA的第m至第n行相对应，则此时心跳二次谐波所在频带的信号可以表示为

(5)

但是应当注意到，式(5)中并未体现各子频带的能量分布特征。

事实上，小波变换属于线性变换，满足能量守恒定律，W各层(对应不同的子频带)的小波系数具有能量量纲，它们的能量分布特征对于信号的频率特性分析是非常有价值的。由于W各层能量的大小反映了原信号更有可能分布在哪些频带，因此可根据能量大小对WMRA进行加权处理，以凸显心跳二次谐波信号更可能出现的频带。将W各层的能量记为[e1，…，eL+1]，则经过能量加权之后的心跳二次谐波信号可以被表示为

(6)

2.3 基于MUSIC算法的频率估计

R=ΦΦH。

(7)

对其进行奇异值分解，可得

R=UDVH。

(8)

由于是在心跳二次谐波频谱范围内进行频率估计的，此范围内的呼吸谐波、呼吸心跳交调谐波的强度几乎可以忽略[15]，且对各层以能量大小进行了加权处理，能量较小频带的贡献进一步被削弱，因此可以将信号的模型阶数定为1，即可认为仅有心跳二次谐波一个信号存在。所以此时的噪声子空间可以表示为Un=U(∶，2∶K)，故而MUSIC谱峰可以表示为

(9)

3 实验结果及分析

3.1 实验设置

雷达传感器设置：实验使用德州仪器(TI)公司的IWR1642雷达传感器采集胸壁运动信号。实验中传感器参数设置如下：起始频率为77 GHz，调频率为66.626 MHz/μs，Chirp脉冲宽度为60 μs，每个Chirp的ADC采样数为256，快时间采样率为5 MHz，每帧包含128个Chirp，帧的周期为40 ms，采用一发一收模式采集胸壁运动信号。

实验场景设置：如图3所示，在书房环境下采集数据，胸壁与雷达之间的距离约在0.55～0.95 m之间，门、墙等距离雷达大约1.7 m，书柜侧壁距离雷达大约1 m。测量时，被测者静坐于雷达前，并保持自然呼吸状态。

图3 实际测量场景

参考标准：以力康PC-3000多参数监护仪获取的心率数据(ECG)为参考，其测量的心跳R-R间期被转化为每分钟跳动次数。心率监测时，监护仪和IWR1642雷达传感器同时进行测量，其中监护仪需要在胸壁黏贴导联电极贴片。

3.2 测量结果及其分析

在心率监测时，由于雷达参数设置为128个Chirp每帧，因此既可以每帧仅抽取1个Chirp进行心率估计，也可以每次每帧仅抽取1个Chirp，然后重复128次，再对128个测量结果取均值的方式估计心率，文中选择后一种方式。在进行数据处理时，时间窗长为5.12 s，每隔0.72 s滑动1次。对于可能出现的野值，采用类似于文献[16]中的方法消除。为验证提出方法的有效性，实验时文献[7]中的方法仅在信号重构与谱估计阶段与提出方法有所差异，其他环节两者均采用相同的处理技术。

3.2.1 加权重构效果分析

为了验证提出的心跳二次谐波信号加权重构方法的有效性，图4给出了加权之前、之后心跳二次谐波信号重构的时域与频域波形图。如图4(a)中2个圆圈内的时域波形所示，重构信号加权处理之前，时域波形存在着一些幅度较小的快速波动，而加权处理之后，这些快速波动信号将被平滑掉。如图4(b)所示，这些快速波动代表着高频噪声或干扰成分，它们会导致心跳二次谐波信号频谱向更高的频带上偏移，从而使得估计的心跳二次谐波频率与参考值对应的2倍频率之间出现较大的偏差。但依据能量大小对各子频带进行加权重构之后，高频噪声或干扰明显被削弱，心跳二次谐波信号将被凸显出来，进而有利于心率估计准确性的提升。

(a) 信号时域波形图

(a) 第1人次测量结果

3.2.2 心率测量结果分析

为评价心率测量结果的有效性，平均值、平均值相对误差(ARE)、平均绝对误差(AAE)和平均绝对误差百分比(AAEP)这4个常用统计指标被用来衡量测量值与参考值之间的误差大小[9，17]。其中后三个指标定义如下：

(10)

(11)

(12)

其中，N、hest(n)和href(n)分别表示总的心率监测次数、第n次心率的测量值和参考值。

实验数据来自6人次，测量对象为成年男女，其中第1人次为女性，其他人次均为男性。测量时胸壁与雷达之间的距离约为0.55～0.95 m。部分测量结果随时间变化曲线如图5所示。

如表1所示，通过文中方法获取的平均心率与监测仪相比，两者非常接近。表2中给出的平均心率相对误差进一步说明了文中方法能够准确地监测平均心率。相比之下，文献[7]中的方法获取的平均心率与参考值之间存在较大误差。

表1 各人次测量的心率平均值 次/分钟

表2 各人次测量的平均心率相对误差(ARE) 次/分钟

表3和表4中分别给出了各人次测量的平均绝对误差和平均绝对误差百分比，这两个统计参数再次表明文中提出的心跳二次谐波加权重构方法，能够获得更加准确的心率测量结果。值得注意的是，第5、6人次测量值与参考值之间差异相对较大，主要原因在于此时雷达与胸壁之间的距离相对较大，从而导致信噪比降低，进而使得测量精度有所下降。

表3 各次测量结果的平均绝对误差(AAE) 次/分钟

表4 各次测量结果的平均绝对误差百分比(AAEP) %

文献[9]使用80 GHz FMCW雷达进行心率监测，当胸壁距离雷达1 m时，其平均心率的相对误差在1.67%～39.24%之间，误差的中值为8.09%。相比之下，文中提出方法在胸壁与雷达之间距离0.55～0.95 m时平均心率的相对误差为0.01%～3.14%(见表2)。此外，文中方法与文献[7]均使用了多分辨率分析，但不同之处在于文中方法考虑了各子频带能量分布特征对心跳二次谐波重构的影响，通过能量加权处理，凸显了二次谐波更可能出现的频带，使得心率估计精度得以明显提升。例如，实验中时间窗为5.12 s时，最小平均绝对误差仅为2.77次/分钟，最小平均绝对误差百分比仅为4.50%，明显优于文献[7]中的方法。因此，与文献[9]和文献[7]中相同频段雷达心率监测方法相比，文中方法有着更高的测量精度。

4 结束语

根据多分辨率分析的结果，将各频带能量分布信息引入到心跳二次谐波的重构之中，利用77 GHz FMCW雷达实现了短时窗高精度的心率估计。在胸壁运动信号多分辨率分析之后，提出方法依据能量大小对心跳二次谐波范围内的各子频带进行加权重构，这不仅有助于凸显心跳二次谐波最可能出现的频率范围，而且也有效避免了呼吸及其谐波的强干扰和模型阶数选择难题。实测数据表明，与其他77 GHz雷达测量方法相比，笔者提出的方法有着较高的心率测量精度。在现有工作基础上，未来将着重研究时间窗更短的瞬时心率估计方法，以便于进一步分析心率变异性。