基于模型预测控制的船舶纵向航速协同控制方法*

吴文祥 初秀民 柳晨光▲ 毛文刚

（1.武汉理工大学国家水运安全工程技术研究中心 武汉430063；2.武汉理工大学智能交通系统研究中心 武汉430063；3.武汉理工大学能源与动力工程学院 武汉430063）

0 引 言

伴随着新一代通信技术、人工智能、物联网等技术的快速发展，船舶自主编队航行、多船协同作业已逐渐成为可能[1]。多船协同航行是指多艘船舶以协作方式完成航行任务，在海事搜救、资源勘探、极地航运等领域中具有显著优势，是智能船舶和智能航运发展的重要趋势[2]。在智能载具协同控制方面，车辆协同控制开展较早，车辆的自适应巡航控制、列队驾驶、编队控制等方面取得了很多进展。目前，船舶协同控制主要在开阔水域开展，难以满足船舶在港口、船闸等复杂航行水域协同航行控制的要求。精确、稳定、可靠的船舶纵向航速协同控制是实现船舶之间安全距离保持、停船、靠泊控制的关键，也是实现船舶协同控制的基础。

针对船舶航速控制问题，常用的控制方法有PID、最优控制、滑模变结构控制、反步法控制等。Kumarawadu等[3]提出了1种基于Lyapunov理论的无人艇航速控制器，可实现潜式三体无人艇纵向、横向和航向相互耦合的功能，并保证了其稳定性。Shojaei等[4-5]为保证航速控制系统对波浪和海流引起的不确定非线性和环境干扰下的鲁棒性，在控制系统中引入了径向基函数神经网络和自适应鲁棒控制技术，并通过仿真证明了该控制器在海上实际应用的可能性。李娟等[6]对船舶的纵向速度误差和横向速度误差进行了积分滑模面的设计，增加了船舶航速控制系统的鲁棒性。王珍[7]提出了基于自适应反演误差补偿的随机风浪下船舶航速控制方法，提高了船舶航行的稳定性。虽然目前已开展了很多船舶航速控制方面的研究，但外界干扰往往难以对船舶纵向动力模型进行精确建模，同时控制输入同时也受到很多约束，这使得精确、可靠的船舶航速控制仍具有较大的难度。

船舶纵向航速控制的最终目的是为了实现多船纵向自动跟驰。朱俊[8]借鉴国外学者伽赛斯在1961年提出的跟驰理论的一般公式研究了内河航道的通航能力。明力等[9]应用交通流跟驰理论，研究超大型船舶纵向间距，建立超大型船舶安全纵向间距计算模型，并分不同情形给出了计算实例。李振福等[10]根据国外学者Gipps 提出的基于安全距离的跟驰理论建立了北极航线船舶航行安全的跟驰模型。目前国内外对于船舶跟驰模型的研究已有一定基础，但基于各种跟驰理论的船间距模型非线性较高，较少应用于船舶的跟驰控制中。

在纵向速度协同控制方面，目前主要研究车辆自适应巡航控制系统（adaptive cruise control，ACC）问题，自从第一代自适应巡航控制（ACC）装备的车辆被投放市场以来已经超过20 年了[11]。Li等[12]基于MPC方法设计了考虑舒适性、经济性、安全性等多目标协调式ACC系统。Hu等[13]设计1种同时兼顾时间效率和精度的算法，将基于Q学习的自适应巡航控制策略与现有的跟踪控制结构相结合，使车辆在弯道上减速，在直线上加速。Kim等[14]研究了基于车辆性能的自适应巡航控制中考虑控制车辆的参数以及不确定性的重要性，并通过3种确定性设计优化（deterministic design optimisation，DDO）的实例，证明了考虑车辆参数以及不确定性的有效性。王文飒等[15]设计了基于深度强化学习的协同式自适应巡航控制框架，并提出了双经验池和优化评价的深度确定性策略梯度算法来解决传统协同式自适应巡航控制算法响应慢、精度不够高的问题。赵树恩等[16]提出了1 种基于显式模型预测控制（explicit MPC，EMPC）理论的车辆多目标自适应巡航控制方法，兼顾了车辆自适应巡航控制系统的跟踪控制效果和实时性。黄菊花等[17]结合卡尔曼滤波器和模型预测控制器设计了1种具有自适应补偿能力的反馈校正模型预测控制器，有效地提高了ACC系统的跟车安全性和乘坐舒适性，并且系统具备良好的抗干扰能力。

目前纵向列队速度协同控制的研究在车辆领域已十分成熟，由于船舶只有在进行特殊任务时才会进行纵向跟驰，例如：在破冰船护航下的船舶跟驰、在狭窄水域进行纵向编队等，所以纵向速度协同控制的研究很少应用在船舶领域。在车辆自适应巡航中，由于车辆加速和制动时加速度变化过快，很难获得前车准确的实时加速度，所以一般将其视为干扰量来处理，一定程度上会影响控制精度。

综上所述，近年来对于船舶航速控制、跟驰模型以及航速协同控制的研究都取得了一定的成果，但也存在一些不足，主要表现在：目前基于各种跟驰理论的船间距模型非线性较高，应用于船舶纵向航速协同控制会影响控制的实时性；在纵向航速控制的研究中，应用于实际应用时，环境或是控制系统自身结构决定着执行器的输出及变化能任意大，因而控制输入同时也受到很多约束，在满足约束条件下控制器的实行变得困难。为了提高船舶在执行特殊任务时的效率，例如在破冰船护航下的船舶跟驰任务、在狭窄水域进行纵向编队任务等，船舶纵向航速协同控制的研究显得十分重要，但目前纵向速度协同的控制的研究主要集中在车辆领域，船舶领域较少。本文在参考了车辆自适应巡航控制系统后，针对船舶纵向航速协同控制问题，采用基于变时距策略的跟驰距离模型解决了船间距模型非线性较高的问题，在建立运动学模型时考虑了前船加速度的影响从而提高了模型精度，最后在结合了船舶的纵向动力模型和运动学模型后，采用MPC解决船舶纵向航速协同控制问题，满足了多约束、高精度、强鲁棒等控制要求。

1 船舶的纵向动力模型

船舶纵向动力模型是分析船舶在航行过程中船舶纵向合力与航速之间的关系。船舶纵向合力由船舶螺旋桨产生的推力与航行所受到的阻力所组成，所以船舶前进动力见式（1）。

式中：T为船舶前进动力，N；Tp为船舶的推进力，N；R为船舶航行时的总阻力，N。

1.1 阻力模型

船舶在水中航行时所受的阻力由静水阻力、风阻以及浪阻形成，而本文考虑的是船舶在波浪较小的情境下，所以暂不考虑波浪阻力，只考虑静水阻力以及风阻，船舶航行时所受的总阻力见式（2）。

式中：R1为静水阻力，N；R2为风阻，N。

船体所受的静水阻力由摩擦阻力、剩余阻力和附体阻力组成[18]，见式（3）。

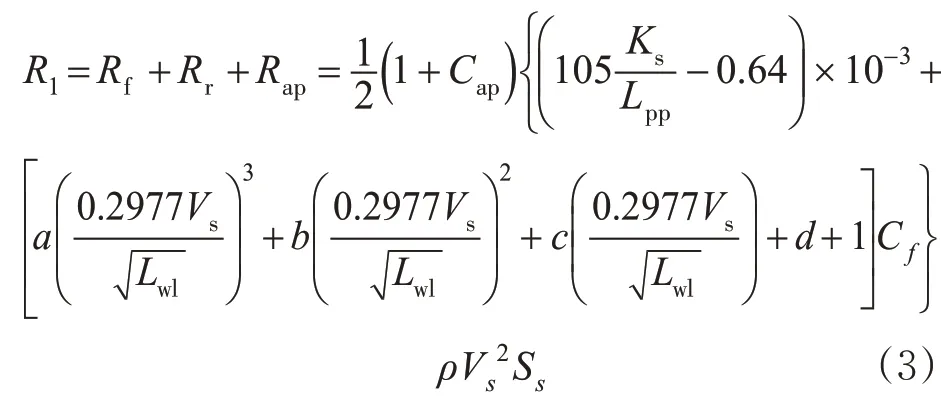
式中：Rf为摩擦阻力，N；Rr为剩余阻力，N；Rap为附体阻力，N；Cap为附体阻力系数；Ks为50 mm长度内的平均波动幅度；Lpp为船舶垂线间长，m；abcd为与船体的瘦长程度相关的系数值；Vs为船舶航速，m/s；Lwl为船舶的水线长度，m；Cf为摩擦阻力系数；ρ为海水密度，kg/m3；Ss为船体表面润湿面积，m2。

摩擦阻力系数Cf的计算公式可表示为

式中：v为海水的运动黏度，m2/s。

船舶风阻经验公式见式（5）[19]。

式中：Ca为空气阻力系数，与船型相关；ρa为空气密度，kg/m3；A为中横剖面投影面积，m2；Va为相对风速，m/s；相对风速可由式（6）计算。

式中：Vw为风速，m/s。

综合式（2）～（6），船舶总阻力见式（7）。

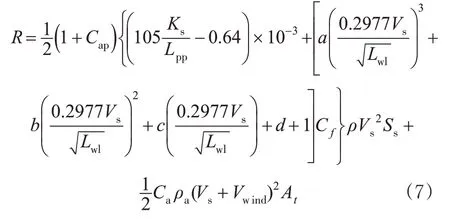
1.2 船舶的推力模型

船舶航行动力由螺旋桨提供，其推进力Tp为式中：k为推力系数；n为螺旋桨转速，r/s；D为螺旋桨直径，m。

推力系数k与进速系数J之间的关系一般为二次方关系[20]，见式（9）。

式中：e1，f1，h1为与螺旋桨螺距比有关的系数值。进速系数J的计算见式（10）。

式中：w为伴流率系数，一般与船型有关。

综合式（8）～（10），可得船舶推进力模型见式（11）。

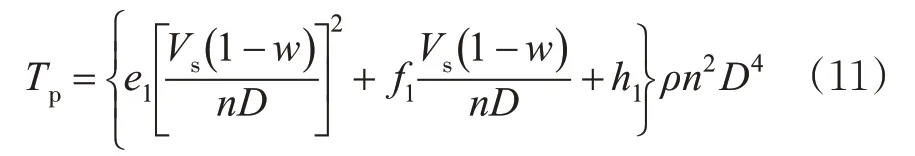
船舶进行加速度较大的减速运动或制动时，螺旋桨将逆转，推力系数kt与进速系数J之间的关系会发生变化，但也可估做二次方关系，所以倒车拉力见式（12）。

2 船舶航速跟驰建模

2.1 基于时变策略的船舶间距模型

船舶间距策略是船舶跟驰的重要组成部分，它决定了整个控制过程中的理想跟船距离，合理的间距策略是保证船舶行驶安全和提高通航效率的关键。本文采用适应性和安全性更好的变时距模型[21]设计船舶间距模型。期望行船间距见式（14）。

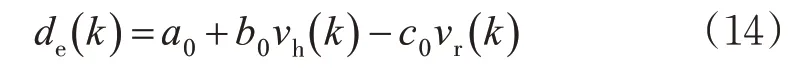
式中：a0，b0，c0为设定参数；vh(k)为主船船速，m/s；vr(k)为2船相对速度，m/s。

船舶的跟驰原理见图1。图中：dr(k)为2 船之间的相对船距，m；vt(k)为 前船船速，m/s；ed(k)为实际距离与期望间距的差值，m。

图1 船舶跟驰示意图Fig.1 Ship following

2.2 船舶的运动学模型

假设k时刻主船加速度为ah(k)，目标船加速度为at(k)，则船舶的运动学模型见式（15）。

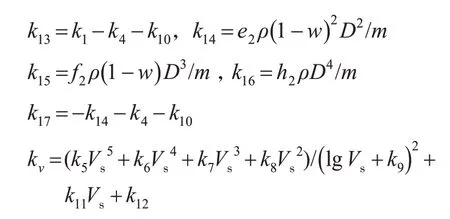
模型中的参数k1～k17可通过最小二乘法辨识得到。设x1=dr(k)，x2=vt(k)，x3=vh(k)，d0为2 船初始相对距离，v0为主船初始船速，m/s；v0'为前船初始速度，m/s；模型的状态方程见式（17）。

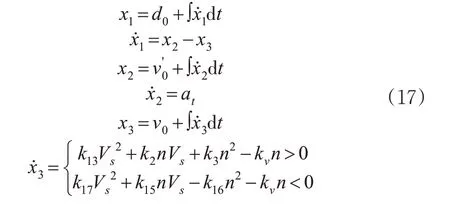
模型经过离散化后，相对船速、距离及主船船速表达式见式（18）。

式中：Ts为采样时间，s。

在车辆自适应巡航中，由于车辆加速和制动时加速度变化过快，很难获得前车准确的实时加速度，一般将其视为干扰量来处理，但是前车加速度的绝对值较大时，加速度的实测值与估算值的误差对于2车之间距离的变化有一定的影响，从而影响控制精度。而在船舶的加速和制动时，船舶的加速度变化较慢，可通过测量获得前船较为准确的实时加速度，且船舶的加速度的绝对值较小，加速度的实测值与估算值的误差对前后船之间距离的变化影响较小，可直接将前船的加速度作为状态量考虑到预测模型中，对控制精度不会产生较大影响。所以在建立实时线性系统时，前船加速度也可以作为输入的状态变量带入模型。

选取主船的加速度为控制变量，相对距离、相对船速、主船船速、前船加速度作为输入的状态变量，得到式（19）。

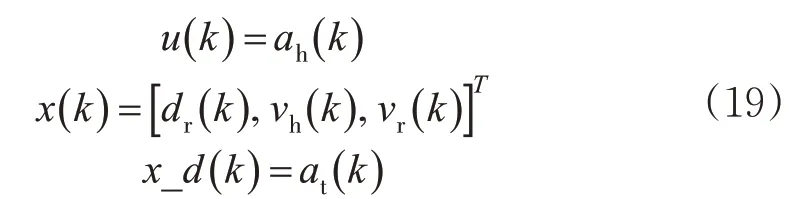
因为输入变量可测，由式（18）可以获得控制主船加速度的预测模型的状态方程，见式（20）。

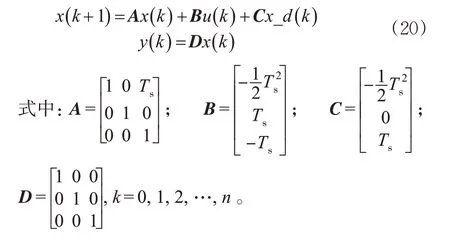
3 模型预测控制

模型预测控制的原理是根据当前时刻测量输出和参考量，求解在预测步长内的最优预测控制输入序列，使得以预测输出和参考量定义的目标函数最小，将最优预测控制输入序列中的第1 个控制输入作为当前时刻的系统控制输入，当其输入系统后，在下1个时刻又重复刚刚的计算过程，从而得到下1个时刻的最优系统输入，这种滚动优化的策略能够保证每一步的输入都是基于当前状态计算到的最优值，保证控制的高精度和强鲁棒。

3.1 基于MPC原理的预测模型

设k时刻后，输入发生P步变化后稳定，且有N≥P，则未来N个时刻系统输入变量的表达式见式（21）。

3.2 约束设置与最优化求解

船舶纵向航速协同控制需要在保证安全性的同时兼顾船舶主机转速限制的前提下实现跟船功能，因此优化目标可以定为减小跟踪误差，约束船速、加速度的变化频率和幅度，抑制过大的振荡。见式（26）。

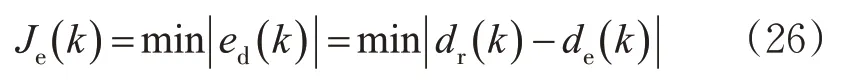
式中：Je(k) 为跟船的误差最优化值，m。跟船的最终目标是在一定时间内与前船船速保持一致，所以相对船速应满足式（27）。

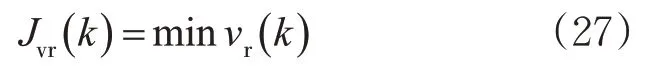
式中：Q 和R 为权重矩阵，可根据控制需求的不同而更改权重大小。

4 仿真验证

4.1 动力模型参数辨识

本文选取被广泛使用和认可的MSS（marine systems simulator）仿真工具箱中的“container”船舶，船长175 m，螺旋桨转速范围为0～160 r/min。首先通过参数辨识获得船舶动力学参数，使用最小二乘法，采用船舶初速度7 m/s，螺旋桨转速150 r/min 的直航运动仿真，k9可以通过工具包提供的参数计算得到，其余参数可以通过工具箱获得的船舶加速度和螺旋桨转速的仿真数据进行参数辨识得到k13，k2，k3，k5，k6，k7，k8，k9，k11，k12的参数值，分别为-2.943×10-4，-6.521×10-5，1.007×10-5，1.042×10-8，-7.356×10-7，2.218×10-5，1.524×10-6，6.240，6.520×10-7，-1.007×10-9。为验证辨识结果的准确性，利用辨识所得的参数对3 组直航运动仿真进行仿真预报，第1 组是对初速度3 m/s 螺旋桨转速80 r/min 的直航运动的仿真与预报，第2 组是对初速度10 m/s螺旋桨转速140 r/min的直航运动的仿真与预报，第3 组是对初速度17 m/s 螺旋桨转速100 r/min的直航运动的仿真与预报，结果见图2。

图2 预报仿真Fig.2 Forecast simulation

图中u1，u2，u3分别为第1/2/3组MSS仿真出的航速曲线，LS1，LS2，LS3分别为第1/2/3 组模型预报出的航速曲线，根据结果可看出辨识出的模型参数具有较高的准确性。由于仿真包中螺旋桨转速只能正转，但在实际运动中，船舶做减速或制动运动时，可通过螺旋桨反转实现，这里假定螺旋桨的反转时，k14和k15分别是k2和k3的80%。

4.2 基于MPC的航速协同控制仿真

4.2.1 前船做加速运动的工况仿真

假设前船初始速度为6 m/s，以0.02 m/s2的加速度进行加速运动，加速至8.00 m/s后进行匀速运动，主船初始速度为5.00 m/s，采样时间设置为1 s，并设置了[-0.005，0.005]的均匀随机数作为对船舶加速度的随机干扰，对该工况进行仿真，基于MPC的航速协同控制仿真结果见图3～6。在相同工况下，基于PID 的航速协同控制仿真结果见图7～10，PID参数分别为Kp=-350；Ki=0；Kd=0。

在此情境下，在基于MPC的航速协同控制的仿真中，船舶跟随的期望距离与船舶之间的实际距离在108 s 时误差已收敛在0.15 m 以内，且平均误差为2.114 5 m，收敛在0.15 m 以内之后的平均误差为0.092 5 m；而在基于PID的航速协同控制的仿真中，船舶跟随的期望距离与船舶之间的实际距离在120 s时误差才收敛在0.2 m以内，且平均误差为3.369 2 m，收敛在0.2 m以内之后的平均误差为0.163 6 m。

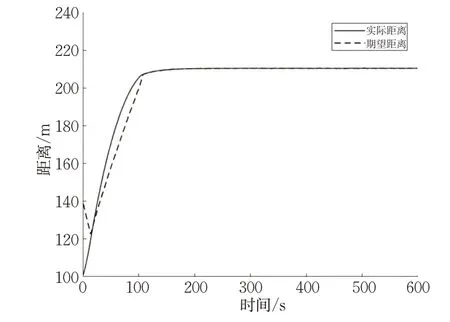
图3 船舶跟驰期望距离与实际距离Fig.3 Expected and actual distances of ship following

图4 前船速度与主船速度Fig.4 Speeds of the forward and lead ships

图5 前船加速度与主船加速度Fig.5 Accelerated speeds of the forward and lead ships

图6 主船螺旋桨转速Fig.6 Propeller speed of the lead ship

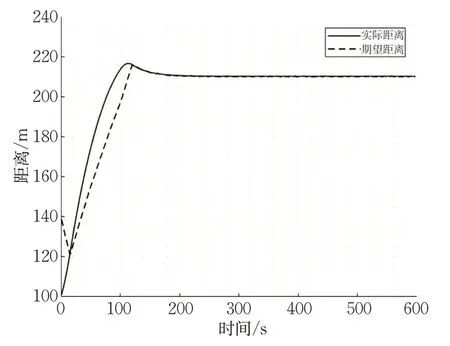
图7 船舶跟驰期望距离与实际距离Fig.7 Expected and actual distances of ship following

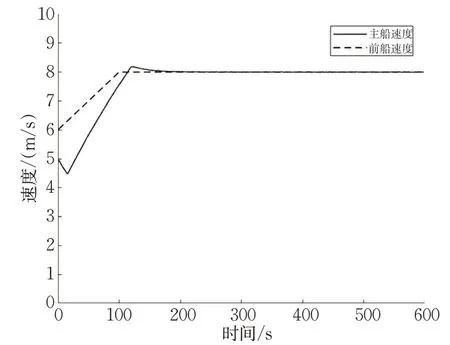
图8 前船速度与主船速度Fig.8 Speeds of the forward and lead ships

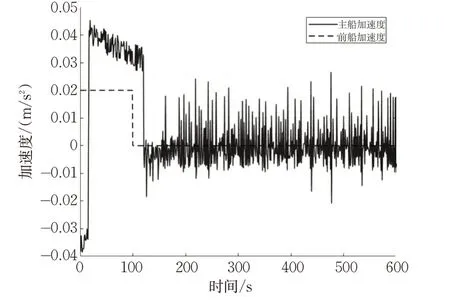
图9 前船加速度与主船加速度Fig.9 Accelerated speeds of the forward and lead ships

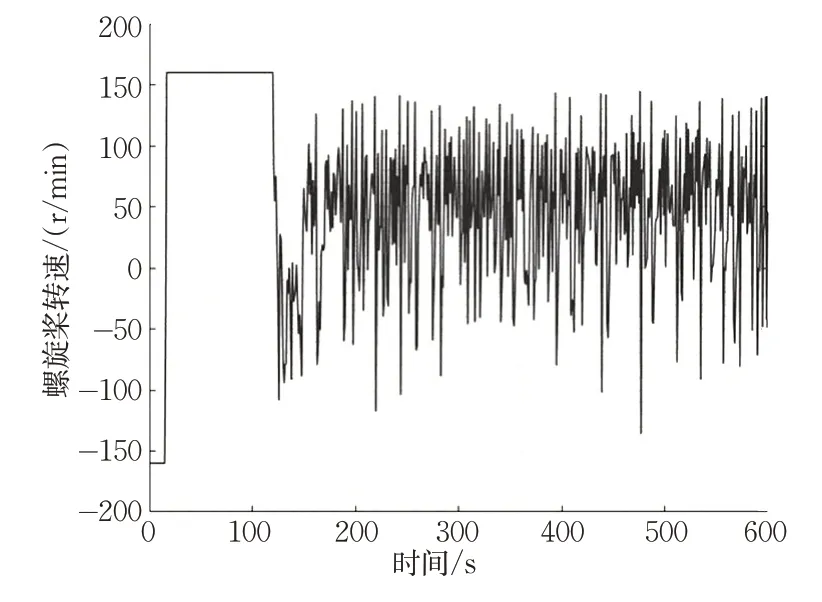
图10 主船螺旋桨转速Fig.10 Propeller speed of the lead ship

4.2.2 前船做减速运动的工况仿真

假设前船初始速度为6 m/s，做加速度-0.02 m/s2的加速运动，减速至4 m/s后做匀速运动，主船初始速度为5 m/s，采样时间为2 s，并设置了[-0.005，0.005]的均匀随机数作为对船舶加速度的随机干扰，对该工况进行仿真，基于MPC的航速协同控制仿真结果见图11～14。在相同工况下，基于PID 的航速协同控制仿真结果见图15～18，PID 参数分别为Kp=-130；Ki=-12.5；Kd=-1。

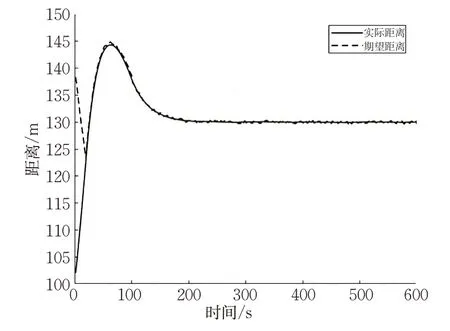
图11 船舶跟驰期望距离与实际距离Fig.11 Expected and actual distances of ship following

图12 前船速度与主船速度Fig.12 Speeds of the forward and lead ships

图13 前船加速度与主船加速度Fig.13 Accelerated speeds of the forward and lead ships

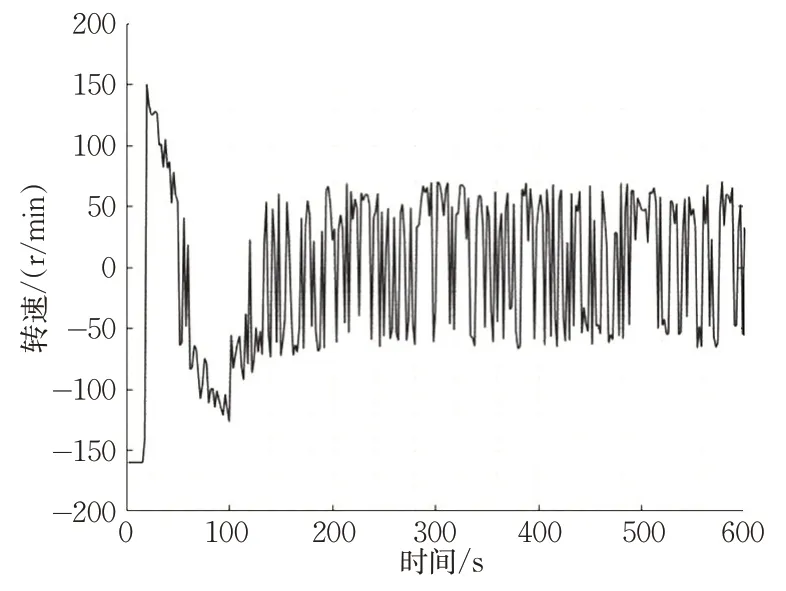
图14 主船螺旋桨转速Fig.14 Propeller speed of the lead ship

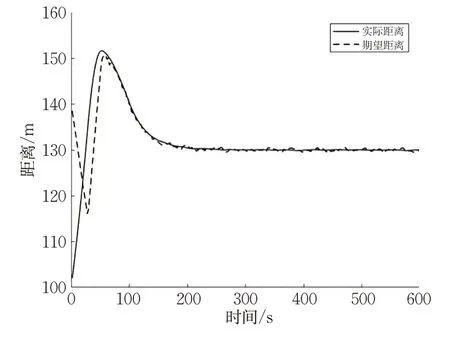
图15 船舶跟驰期望距离与实际距离Fig.15 Expected and actual distances of ship following

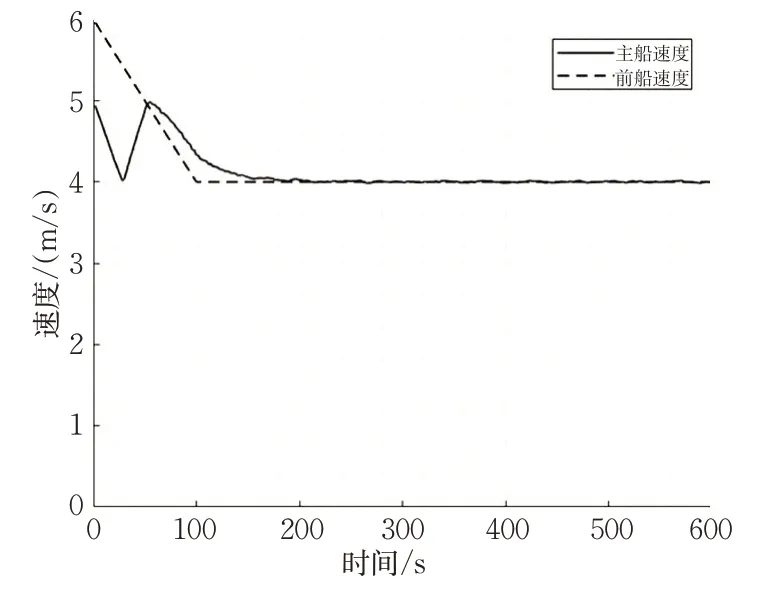
图16 前船速度与主船速度Fig.16 Speeds of the forward and lead ships

图17 前船加速度与主船加速度Fig.17 Accelerated speeds of the forward and lead ships

图18 主船螺旋桨转速Fig.18 Propeller speed of the lead ship

在此情境下，在基于MPC的航速协同控制的仿真中，船舶跟随的期望距离与船舶之间的实际距离在20 s时误差已收敛在0.25 m以内，且平均误差为0.814 8 m，收敛在0.25 m 以内之后的平均误差为0.192 8 m；而在基于PID 的航速协同控制的仿真中，船舶跟随的期望距离与船舶之间的实际距离在60 s 时误差才收敛在0.3 m 以内，且平均误差为1.574 7 m，收敛在0.3 m 以内之后的平均误差为0.244 1 m。

4.2.3 前船做匀速运动的工况仿真

假设前船初始速度为6 m/s，做加速度为0 m/s2的匀速运动，主船初始速度为5 m/s，采样时间为2 s，并设置了[-0.005，0.005]的均匀随机数作为对船舶加速度的随机干扰，对该工况进行仿真，基于MPC 的航速协同控制仿真结果见图19～22。在相同工况下，基于PID 的航速协同控仿真结果见图23～26，PID 参数分别为Kp=-180；Ki=-12；Kd=-1。

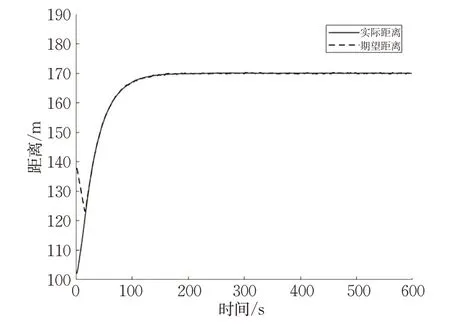
图19 船舶跟驰期望距离与实际距离Fig.19 Expected distance and actual distance of ship following

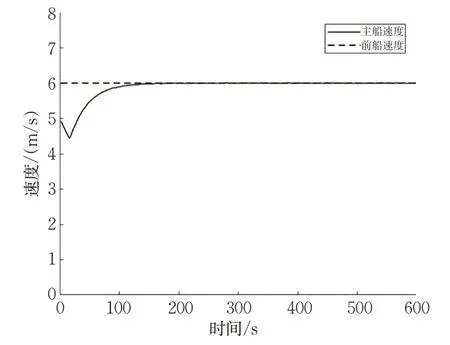
图20 前船速度与主船速度Fig.20 Speeds of the forward and lead ships

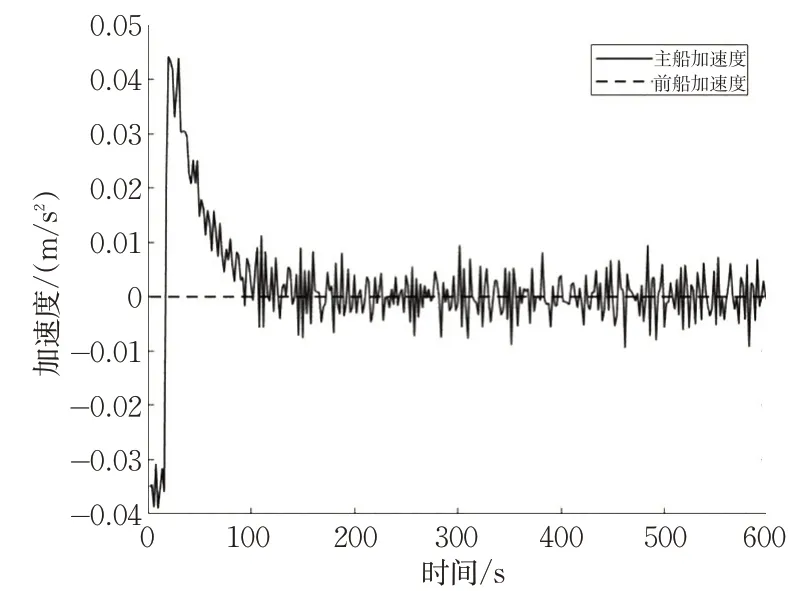
图21 前船加速度与主船加速度Fig.21 Accelerated speeds of the forward and lead ships

图22 主船螺旋桨转速Fig.22 Propeller speed of the lead ship

图23 船舶跟驰期望距离与实际距离Fig.23 Expected and actual distances of ship following

在此情境下，在基于MPC的航速协同控制的仿真中，船舶跟随的期望距离与船舶之间的实际距离在20 s 时误差已收敛在0.2 m 以内，且平均误差为0.692 5 m，收敛在0.2 m 以内之后的平均误差为同控制仿真结果都优于基于PID的航速协同控制的仿真结果，螺旋桨转速的变化幅度也相对较小，能相对的节约能耗，增加主机螺旋桨寿命，且在控制调节中，对于不同工况MPC相比PID的适应性更强。

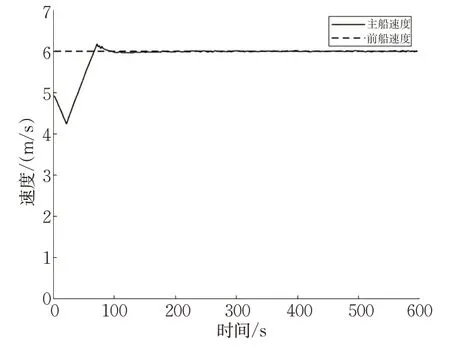
图24 前船速度与主船速度Fig.24 Speeds of the forward and lead ships

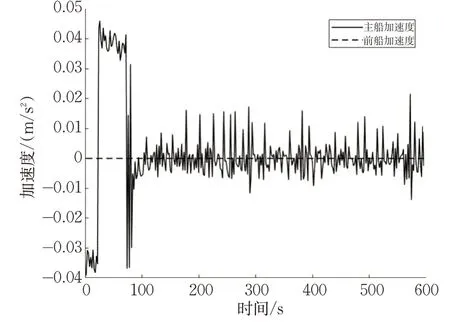
图25 前船加速度与主船加速度Fig.25 Accelerated speeds of the forward and lead ships

图26 主船螺旋桨转速Fig.26 Propeller speed of the lead ship

5 结束语

笔者提出了变时距策略建立了船间距模型，以及船舶纵向动力学模型与船舶运动学模型，提出了基于模型预测控制的船舶航速协同控制器，并验证了其控制效果。设计的航速协同控制器可为船舶在狭窄水域纵向列队航行控制器的设计提供重要依据。

本文的研究是在波浪较小的情况下进行的，忽略了波浪、横漂力以及首摇力矩对前进力的影响，可能会影响控制精度。此外，在后续的研究中可考虑内部不确定因素以及浪的影响，并可将横漂力以及0.166 2 m；而在基于PID 的航速协同控制的仿真中，船舶跟随的期望距离与船舶之间的实际距离在140 s 时误差才收敛在0.3 m 以内，且平均误差为2.325 8 m，收敛在0.3 m 以内之后的平均误差为0.277 4 m。

综上所述，在3 种不同工况下，基于MPC 的航速协同控制仿真与基于PID的航速协同控制仿真结果见表1。基于MPC的航速协同控制在3种工况下都有较好的跟驰效果，且无论是在收敛速度、平均误差方面还是在抗干扰能力方面，基于MPC的航速协首摇力矩对前进力的影响也视作外界干扰，通过设计观测器对干扰进行估计，提高控制器精度。

表1 仿真结果Tab.1 Simulation results

船舶执行某些任务时需特殊的航行环境中进行，例如北极科考时需在北极航行或者通过某些船闸或者海峡港口时需在狭窄水域航行。在北极航行时，为保障船舶进出冰封港口、锚地，或引导船舶在冰区航行，往往需要破冰船开辟航道，后船再对破冰船进行纵向跟随，距离过进容易出现安全隐患，距离过远容易导致跟随船还未行进，已经开辟的航道上水面就已经重新结冰或者出现航道外漂浮而来的其他冰块，导致跟随船依然无法航行；在狭窄水域航行时，考虑安全性，船舶无法并行通过时，需要进行纵向列队通过，船间距过近时，容易出现安全隐患，船间距过远时，在本就狭窄的航道中极大的降低了通行效率，浪费航道资源。基于以上分析，本文提出的纵向航速协同控制可以为相关研究提供参考。