基于Boussinesq 水波模型的聚焦波模拟

刘必劲，张振伟，刘忠波，傅丹娟，陈小云

(1.厦门理工学院 土木工程与建筑学院，福建 厦门 361024；2.大连海事大学 交通运输工程学院，辽宁 大连 116026)

1 引言

畸形波是一种非线性很强的波浪，其波高很大，通常是有效波高的2.2 倍以上，这种波浪对海上建筑物或过往的船只带来严重威胁。为了深入掌握畸形波的形成机制，国内外学者通过理论分析、数值模拟或实验模拟等方式展开了数十年的研究。2003 年，Kharif 和Pelinovsky[1]较为全面地分析了其形成机制，认为在相位聚焦、波−流相互作用、地形变化、表面风、波浪不稳定性等影响下都可能产生畸形波。

为了研究畸形波，实验室中一般都采用相位聚焦的方式产生较大的波浪，如Baldock 等[2]在二维水槽中采用线性相位聚焦的方式产生了聚焦波；柳淑学和洪起庸[3]在三维水池中开展了三维极限波浪的实验研究。在理论分析方面，裴玉国等[4]采用线性模型模拟了定点生成畸形波的方法；赵西增等[5]则借助于聚焦波和不同形式波浪的组合模拟畸形波。在数值模拟方面，国内外学者则通过利用N-S 方程模型、非静压模型、Boussinesq 方程数值模型、势流方程模型、高阶谱模型等不同的数学模型模拟聚焦波。如赵西增等[6]利用高阶谱方法建立了模型，并应用于畸形波的模拟；Li 和Liu[7]建立了非周期边界的高阶谱聚焦波模型，并研究设定聚焦波幅、中心频率、频率宽度、波幅分布以及方向角等对聚焦波的影响，研究表明，宽的方向谱减弱了非线性聚焦波幅；Ai 等[8]建立了不同网格下的非静压模型，并模拟了水槽和水池中的聚焦波；Ning 等[9]基于势流理论建立了高阶边界元数值模型，模拟了深水聚焦波；Li 等[10]在CIP 模型（利用CIP 求解对流项）中引入内部造波法，模拟了潜堤上聚焦波的传播变形问题。

关于Boussineq 模型在聚焦波模拟的研究文献相对较少，能成功模拟聚焦波速度分布特征的仅有少数Boussinesq 水波方程，这是因为多数Boussinesq 方程本身在色散性、非线性，特别是速度分布特征方面存在严重不足。分析相关数值模拟聚焦波的研究可知，准确模拟波面传播变形需要数值模型具有良好的色散性与非线性特征，准确模拟速度分布必须要求模型具备良好的速度分布特征。当前能具备这些性能的Boussineq 数值模型并不多，在分析大量Boussineq方程文献基础上，本文选用了一组单层Boussinesq 水波方程，即Liu 和Fang[11]给出的双层Boussineq 模型的简化版。事实上，该简化版本的模型在平底情况下与Madsen 等[12]给出的Boussineq 水波方程完全一致。本文将针对单层Boussinesq 水波方程建立数值模型，并考察其是否能适用于模拟强非线性波浪传播和聚焦波的演化问题。

2 Boussinesq 数值模型

2.1 控制方程

假设水体无旋、无黏，在保留垂向速度下，Liu 和Fang[11]经严格数学推导给出了适合缓变地形的双层Boussinesq 方程，将其简化成为单层方程。立面二维模型由7 个方程组成，含有7 个待求变量：波面位移η，自由表面处水平和垂向速度uη和wη，静止水位处的水平和垂向速度u0和w0以及计算水平和垂向速度u*和w*，方程的具体表达形式如下：

（1）自由面 η处的运动学边界条件和动力学边界条件为

（2）自由面速度（uη，wη）与静止水位处速度（u0，w0）的关系为

（3）静止水位处速度（u0，w0）与计算速度（u*，w*）的关系为

（4）水底处满足的运动学边界条件为

式中，g是重力加速度；下标x表示对x求导；h表示水深；其中(α,β12,β13)=(0.5,0.95,0.55)。

整个流场的表达式分为两部分，从静止水位到波面处的速度表达式为

式中，z表示原点位于静水面时向上为正的垂向位置。从水底到静止水位的速度表达式为

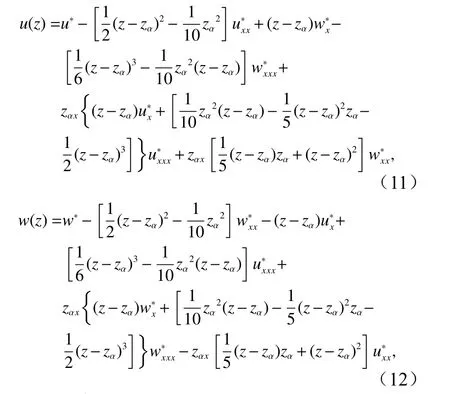
方程（1）至方程（7）构成单层Boussinesq 水波方程，图1 给出了变浅梯度与解析解的对比以及无因次相速度。由图可见，在2%误差范围内，相速度可适用于最大水深k0h=10（k0为深水波数，h为水深）[12]；速度分布特征在1%误差范围内适用的最大水深为k0h=3.5；变浅性能可适用0＜k0h＜10 范围①林鹏程，刘忠波，刘勇.基于Boussinesq 数值模型的波浪速度垂向分布模拟研究.海洋湖沼通报，已采用.。

2.2 数值模型的求解

以上垂向二维Boussinesq 方程中的最高空间导数是3 阶，模型本身与开源代码FUNWAVE 的最高空间导数是一致的[13]，为此时空差分格式均采用与该开源代码一样的格式。在时间差分格式上采用混合4 阶Adams-Bashforth-Moulton 格式，预报时利用3 阶Adams-Bashforth 格式求解方程（1）和（2），可以得到波面位移以及相应的波面处水平速度的预报值；分别求解方程（3）和（5）可得到2 个水平速度的预报值；求解方程（7）、（6）和（4），可依次得到3 个垂向速度的预报值。校正时利用4 阶Adams-Moulton 时间步进格式，求解得到所有变量的校正值。当7 个变量的校正值与预报值之间的误差在0.000 1 内，当前迭代结束，否则用校正值和预报值的加权重新赋值给变量的预报值，本文算例中校正加权值R为0.1～0.2，而预报加权为1-R，并多次重复校正过程，直到满足条件为止。以上过程可以参见文献[13-14]。

图1 方程的变浅梯度（a）和无因次相速度（b）Fig.1 The shoaling gradient (a) and non-dimensional (b)phase celerity of the present model

3 数值模型的验证

为了验证数值模型，我们采用流函数波浪的数值解作为近似的解析解来考察模型的适用情况。数值计算长度设置为10L（L为流函数波浪的波长），在入射边界2 个波长范围内用流函数波浪的解析解作为模拟的驱动条件，并在该范围内采用了Fuhrman[15]提出的边界松弛造波法，这相当于将近似解析解逐渐转化为方程数值解的一种方式。在出口边界，设置了2L的海绵边界层进行消波。在固定波浪周期为6 s情况下，针对水深为20 m、30 m 和40 m 情况下，对波高为6 m 的流函数波浪进行了数值模拟研究。3 种情况对应的流函数波长分别为60.469 m、61.524 m 和61.679 m，无因次水深kh分别为2.078、3.064 和4.074；对应的波陡H/L=0.099、0.098 和0.097；这几组工况的波高约是极限波高的0.7、0.65 和0.64 倍左右，因此属于强非线性波浪算例。

图2 水深为20 m 的计算结果与解析结果的比较Fig.2 Comparisons of analytical solution and numerical simulation for water depth 20 m

图3 水深为20 m 波峰面下的水平速度分布与解析解的比较（x=4L）Fig.3 Comparisons of velocity profile between numerical simulation and analytical solution for water depth 20 m (x=4L)

每一个工况计算时间为300 s，空间计算步长取为L/32，时间计算步长取为0.05 s。将计算得到的波面位移、波面处水平速度与垂向速度以及沿垂向分布的水平速度与近似解析解（流函数波浪的数值解析解）进行了比较，具体结果见图2 至图7。图2、图4和图6 给出了计算波面位移、波面处水平速度与垂向速度与近似解析解的比较；图3、图5 和图7 给出了x=4L波峰面下水平速度的垂向分布与解析解的比较。由图2、图4 和图6 可见，波面以及波面处速度与解析解误差较小，为了明确误差的具体值，计算了波长与解析解的误差（从2L～8L范围内标定），3 种情况下仅第一组误差是0.52%，其他组几乎不存在误差；以2L～8L范围内变量最大值的平均值为统计，最大波峰面与解析解的误差、最大水平速度、最大垂向速度与相应的解析解误差均在1%范围内。进一步，从x=4L波峰面下水平速度（图3，图5，图7）对比来看，伴随水深的加大，波峰面水平速度分布的精确度逐渐变差，这与文献中给出的线性Stokes 波的速度分布与解析解在kh=3.5 的积分误差是1%的规律是类似的，这里不再进行速度分布的积分误差的详细计算。

图4 水深为30 m 的计算结果与解析结果的比较Fig.4 Comparisons of analytical solution and numerical simulation for water depth 30 m

4 聚焦波演化的模拟

图5 水深为30 m 波峰面下的水平速度分布与解析解的比较（x=4L）Fig.5 Comparisons of velocity profile between calculated and analytical solution for water depth 30 m (x=4L)

受水槽长度的限制，实验室中一般采用线性相位聚焦方式产生较大的聚焦波进行物理模型实验。在深水情况下，由于受波浪非线性的影响导致实际聚焦位置与设置的线性聚焦位置存在向后偏移，对应的聚焦时间也会向后偏移。这种偏移是因为聚焦波的波幅增大后，线性波的波长不能诠释聚焦波波幅增加后引起波长增加的现象，其本质就是线性色散关系表达式已经不适用于阐释强非线性的波长，此时应考虑波幅引起色散关系的变化，即波幅离散引起频散。关于这一点在上面的算例中已有相关印证，以第3 个工况为例，线性波长为56.192 m，而流函数波浪的波长为61.679 m，二者误差为9.7%。聚焦波的非线性增强，则这种偏移量越大[2]。

图6 水深为40 m 的计算结果与解析结果的比较Fig.6 Comparisons of analytical solution and numerical simulation for water depth 40 m

图7 水深为40 m 波峰面下的水平速度分布与解析解的比较（x=4L）Fig.7 Comparisons of velocity profile between numerical simulation and analytical solution for water depth 40 m (x=4L)

Baldock 等[2]开展的深水实验含有不同波浪频率段范围，在不同周期内等分周期成29 份，每个频率的波幅取值相等，其中B 组（T=0.6～1.4 s，宽谱）和D 组（T=0.8～1.2 s，窄谱）作为主要参考用来考察本文数值模型，B 组和D 组的线性无因次水深kh分别为1.568～7.825 和2.026～4.403。为了模拟聚焦波的生成过程，本文在入射边界处引入线性解叠加方式，具体做法：给定每一个组成成分的波面位移的时间历程，利用线性化的Boussinesq 方程确定出其他所有变量的时间历程值，详细过程可参见文献[14,16]。设置计算域为24 m，空间计算步长采用0.04 m，时间计算步长为0.01 s，末端设置4 m 的海绵边界层消波，计算时间为40 s。对B 组和D 组的3 种不同设定的聚焦波峰面为22 mm、38 mm 和55 mm 工况进行数值模拟，计算的聚焦位置处的波面位移和最大波峰面下的速度分布与实验结果进行了比较，具体见图8 和图9。整体而论，计算波面位移与实验结果吻合程度较好，水平速度的分布与实验结果基本吻合。宽谱情况下（B 组），计算的水平速度出现“S”形，图9 与图7 的结果有相类似的规律，这是因为数值模型在线性无因次水深kh＞3.5 后误差将逐渐增大，在kh＜3.5 只有18 个组成波在这个范围内；窄谱情况下（D 组），线性无因次水深kh＜3.5 范围内22 个组成波，因此D 组工况比B 组工况模拟效果要好。关于D22 算例数值结果与实验结果吻合程度不好的原因，本文也尝试了采用两个不同的双层Boussinesq 水波方程模型[14,16]；Liu 等[14]数值模拟结果与本文计算结果相差不大，也存在与实验偏差较大的情况，鉴于这一组的波浪非线性相对较弱，因此可以初步认为有可能是实验结果存在一定的偏差。

对于设定聚焦波面为55 mm 的情况，固定波浪中心频率不变，即保持1 s 周期不变，设定线性聚焦位置为8 m，30 s。在周期范围△T分别为0.8 s、0.7 s、0.6 s、0.5 s 和0.4 s 情况下聚焦波时的波峰面、波峰面速度、聚焦时间和空间差等在表1 中给出，时空偏移是数值模型（或实验模型）得到的实际聚焦位置与线性波群设定的聚焦时间和位置之间的偏移量。

5 结论

本文建立了基于单层Boussinesq 水波方程的垂向二维数值模型，首先与流函数波浪解析解进行了对比，并将这个数值模型应用于聚焦波的模拟中，研究得出主要结论如下：

图8 聚焦的计算波面位移与实验波面位移的比较Fig.8 Comparisons of surface elevations between modeled and experimental data

图9 聚焦波峰面下的水平速度与实验结果的比较Fig.9 Comparisons of velocity profiles between modeled and experimental data

表1 计算结果与实验结果的比较Table 1 Comparisons of results between modeled and experimental data

（1）数值模型计算的波面位移、波面位移处的水平速度与垂向速度均与流函数的解析解有较好的吻合，同时垂向速度在适用范围内与解析解的比较，也展示出本文建立的数值模型能够胜任模拟强非线性波浪。

（2）聚焦波演化中，波浪非线性性起重要作用，本文Boussinesq 型方程具有良好的色散性与非线性性能，保证了方程具有模拟聚焦波的能力；数值模拟波面与实验结果的对比，展现了本文Boussinesq 数值模型能够模拟聚焦波波面演化。

（3）与精确模拟的波面相比而言，在模拟速度分布的精度方面，在理论方面，方程的色散适用范围明显大于水深速度分布的适用范围。数值模型受限于线性速度分布的精度，其模拟非线性速度分布的能力也明显受限于kh＜3.5。尽管数值模型可以较为精确模拟波面以及波峰面处的水平速度与垂向速度，但对于kh＞3.5 的组成成分较多的聚焦波，基于本文Boussinesq 水波方程的数值模型无法精准模拟水平速度分布情况。

本文明确了水平速度分布的非线性适用范围，在此基础上可期望将模型拓展到研究聚焦波与建筑物相互作用问题。此时只需将速度表达式（公式（9）至公式（12））代入垂向欧拉方程中，进行两次垂向积分，最终可以得到波浪力，关于这一方面将在下一步进行研究。