网络谣言与恐慌情绪并行传播相互影响研究*

王佳佳 邱小燕

(1．西华大学应急学院 成都 610039；2. 上海应用技术大学经济与管理学院 上海 201418)

0 引 言

近年来，随着微博、微信、社交网站等社会化媒体的广泛应用，使得舆情信息传播变得更加容易，这些舆情信息里充斥着大量的谣言信息，特别是突发事件频发的状态下，人们的措手不及、认知局限和偏差等因素，更是谣言产生和传播的温床。例如，到目前为止还在进行的新冠疫情突发事件，其中的谣言举不胜举。这些谣言深刻地影响着民众的心理与行为。受谣言的影响民众很容易产生消极的情绪。在网络群体的影响下，若消极性的情绪不加以疏导，在网民中传播蔓延，极化后会进一步诱发群体性的过激行为，过激行为又极易演化成为突发事件，便会造成严重的社会后果。因此，在谣言传播的过程中考虑情绪的传播，把谣言与情绪两者结合起来进行研究，对于减少网络舆情及其后续恶化演变给国家、社会及个人带来的损失具有重大意义。

目前，国内外对于谣言传播的研究比较丰富。因为谣言在人际中的传播类似于疾病，所以初期的谣言传播模型大都借鉴了“传染病学”模式分析的方法[1-2]。对于谣言传播定量的研究主要集中在两个方面：一个是谣言的传播规律，另一个是谣言传播的防控方法。谣言传播规律的研究主要经历了小规模社会网络的谣言传播研究阶段[3-4]，考虑网络拓扑结构的研究阶段[5-7]以及考虑心理学特征、个体之间亲疏关系等因素的研究阶段[8-9]。谣言传播防控方法主要分为三大类：一是研究谣言传播本身的自净化过程[10]，二是从谣言传播所在的网络结构特征进行预防和控制[11]，三是施行外部干预策略，如增加政府的辟谣措施[12]、如对网络中的个体进行谣言免疫[13]等。综上可知，谣言传播并不是一个简单的过程，谣言传播的工具和平台越多，谣言传播就越频繁，谣言传播问题也越棘手，学者对谣言传播的研究也越深入。与谣言传播相比，情绪传播方面的文章定性方法的研究多于定量方法。定性的研究多从情绪传播定义、特征、动因、交互感染方式、发展阶段、应对策略等角度进行展开[14-16]。定量的研究主要从实验、系统动力学、元胞自动机等方法研究网络情绪的演化机制[17-19]。这其中，有一大类研究也是借鉴了传染病的研究方法，如Zhao[20]等研究了悲观、乐观两种情绪在受周边环境及社会环境共同影响下的传播转化规律。张亚明[21]等把负面情绪累积效应引入到传染病模型中，构建了网民群体情绪传播模型，讨论了情绪强度、情绪自我调节、政府舆情引导等因素对情绪传播的影响。

纵观上述研究，谣言传播方面的文章大多忽略了群体情绪的讨论。情绪传播方面的文章虽然已经意识到情绪之害的重要性，但是当研究情绪传播的时候，大多是将情绪嵌入到信息之中，而传播的衡量是以谣言或者信息的传播代之。虽然情绪的传播离不开信息的传播，信息当中承载着情绪的表达，但是信息和情绪有着不同的内涵和外延。例如：双黄连能够治疗新冠肺炎这则谣言信息及其引发公众恐慌情绪而更进一步产生抢购双黄连的行为确实是不同的概念。但是现有的文献还没有涉及把信息传播和情绪传播分割开来，区别对待的内容。本研究在谣言传播的基础上，重点关注谣言所引发的恐慌情绪，把恐慌情绪引入到谣言传播模型中，考虑到恐慌情绪的诱发相对于谣言传播和恐慌情绪传播的时间可以忽略不计，因此，本文建立了谣言及恐慌情绪并行传播的双传播模型。应用数学推导及仿真模拟的方法对此双传播模型进行研究，分析了传播阈值的变化特征和它们相互影响的传播规律。此研究理论上可以丰富舆情传播的研究内容，实践中可以为相关部门制定应对突发事件中的舆情决策提供依据。

1 谣言及恐慌情绪双传播模型构建

1.1双传播模型假设Moreno等人[22]给出了谣言传播模型的规范分类方法。他们把人群分为三类，即没有听到过谣言的人(无知者Ignorant，用I表示)、传播谣言的人(传播者Spreader，用S表示)和知道谣言但是并不传播谣言的人(免疫者Stifler，用R表示)，在本文中我们沿用Moreno等关于谣言分类的记号。Zhao等人[20]给出了情绪传播二值分类方法，根据人群情绪状态分为两类：积极情绪状态类和消极情绪状态类。积极情绪状态是指乐观、安心、高兴等积极倾向的情绪状态。具有积极情绪状态的人一般可以客观理智看待问题，不会发生极化情绪。消极情绪状态是指愤怒、恐慌、悲伤等消极倾向的情绪状态。具有消极情绪状态的人当消极情绪累积到一定程度容易出现情绪及过激行为大爆发，进而发生群体性事件。在本文中我们关注的重点是恐慌情绪，所以借鉴Zhao等关于情绪传播的二值分类方法，按照是否具有恐慌情绪，网络中的个体被分为两类：有恐慌情绪者(用+表示)和无恐慌情绪者(用-表示)。

引理1：集合A1,A2,A3两两互不相容，并且满足条件A1+A2+A3=Ω，集合B1,B2满足条件B1B2=∅，B1+B2=Ω，则集合A1B1,A1B2,A2B1,A2B2,A3B1,A3B2两两互不相容，且满足A1B1+A1B2+A2B1+A2B2+A3B1+A3B2=Ω。

证明：∵A1A2=∅，∴A1B1∩A2B1=∅,A1B2∩A2B2=∅。同理∵A1A3=∅，A2A3=∅，∴A1B1∩A3B1=∅,A1B2∩A3B2=∅,A2B1∩A3B1=∅,A2B2∩A3B2=∅。又∵B1B2=∅，∴A1B1∩A1B2=∅,A1B1∩A2B2=∅,A1B1∩A3B2=∅,A2B1∩A1B2=∅,A2B1∩A2B2=∅,A2B1∩A3B2=∅,A3B1∩A1B2=∅,A3B1∩A2B2=∅,A3B1∩A3B2=∅，所以A1B1,A1B2,A2B1,A2B2,A3B1,A3B2两两互不相容。由已知条件∵B1+B2=Ω，∴A1=A1Ω=A1(B1+B2)=A1B1+A1B2，同理A2=A2Ω=A2(B1+B2)=A2B1+A2B2，A3=A3Ω=A3(B1+B2)=A3B1+A3B2。又∵A1+A2+A3=Ω，∴A1B1+A1B2+A2B1+A2B2+A3B1+A3B2=Ω，即引理得证。

按照谣言传播状态把人群分为3类，按照恐慌情绪传播状态把人群分为2类，那么，当同时考虑谣言和恐慌情绪时，即可把谣言传播状态与情绪传播状态分别取交集，得到6个新的集合。根据引理1，这6个集合既没有交集又可以把整个人群全部覆盖。定义这6个集合即6类人分别为：无恐慌无知者(记作I-)、无恐慌传播者(记作S-)、无恐慌免疫者(记作R-)、恐慌无知者(记作I+)、恐慌传播者(记作S+)、恐慌免疫者(记作R+)。谣言及恐慌情绪在人群中传播各类人群状态转移过程如图1所示，其中实线箭头表示需要接触其他状态的人而发生的状态转移，虚线箭头表示不需要接触他人而自发发生的状态转移。

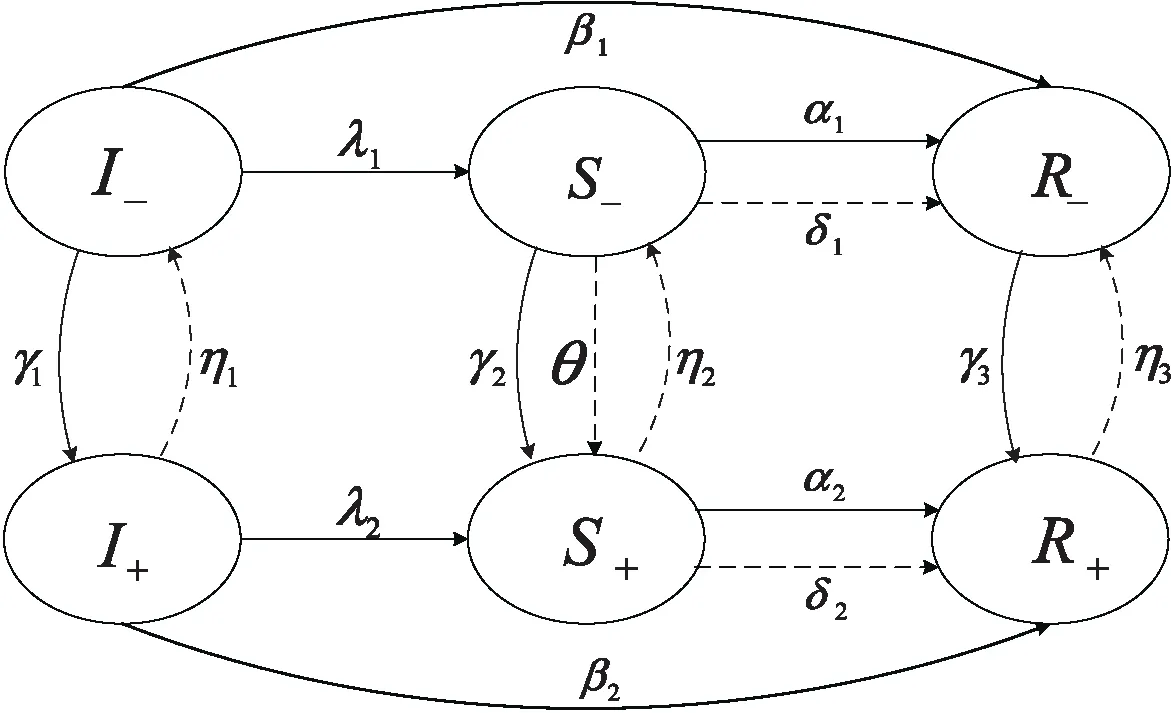
图1 谣言传播及恐慌情绪传播各类人群状态转移图

图1中各参数的定义及其代表的转化概率意义如表1所示。

表1 参数定义及其意义

结合图1，谣言及恐慌情绪双传播模型的演化规则如下所示：

①谣言传播部分依然遵循以往的传播规律，无知者(恐慌/无恐慌)碰到传播者(恐慌及无恐慌)，要么会相信谣言并开始传播从而变为传播者(恐慌/无恐慌)，要么不相信谣言直接变为谣言免疫者(恐慌/无恐慌)。传播者(恐慌/无恐慌)除了碰到免疫者(恐慌及无恐慌)会变为免疫者(恐慌/无恐慌)，还会由于遗忘机制而自发变为免疫者(恐慌/无恐慌)。

②恐慌情绪传播部分，无恐慌情绪者(无知者/传播者/免疫者)碰到恐慌情绪者(无知者及传播者及免疫者)会变为恐慌情绪者(无知者/传播者/免疫者)。随着时间的推移，恐慌情绪者(无知者/传播者/免疫者)会自发地失去恐慌情绪而变为无恐慌情绪者(无知者/传播者/免疫者)。

③谣言引起了恐慌，从无恐慌传播者到恐慌传播者的自发转移来体现，相应的转化概率定义为谣言恐慌率。

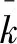
(1)

(2)

(3)

(4)

(5)

(6)

1.3双传播模型稳定性分析

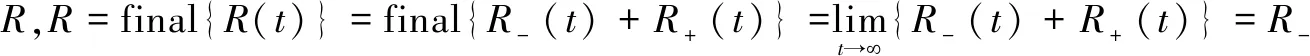
(3)式与(6)式的和除以(1)式与(4)式的和，可以得到：

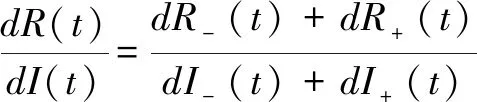
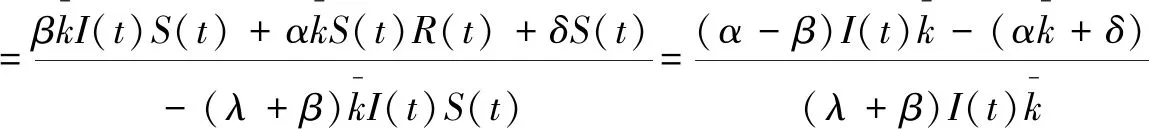
1.3.2 恐慌情绪传播系统稳定性分析 综合谣言分类，恐慌情绪传播方面我们把无恐慌情绪者记作N-(t)，那么有N-(t)=I-(t)+S-(t)+R-(t)，把恐慌情绪者记作N+(t)，有N+(t)=I+(t)+S+(t)+R+(t)。这里假设γ1=γ2=γ3=γ，η1=η2=η3=η，此时可得恐慌情绪传播的平均场方程为：

(7)

(8)

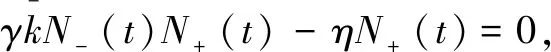
图2 谣言及恐慌情绪独立系统传播阈值区域

2 仿真模拟

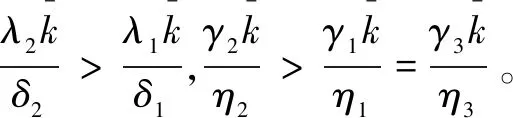
分别利用Runge-Kutta方法及有限差分法模拟均匀网络和人人网络中的谣言及恐慌情绪的传播阈值变化特征及其传播规律。无论在哪种网络中，初始时刻网络中只有一个无恐慌传播者。为了消除人人网络中由于初始传播者随机选择所带来度值大小不同的差异，我们对人人网络中的仿真采取模拟50次计算平均值的方法。

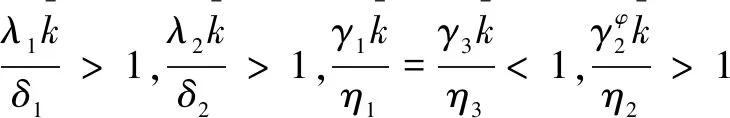
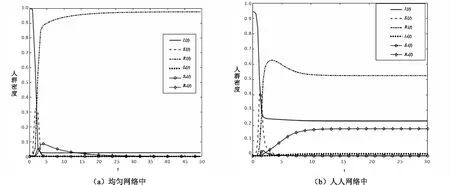
图3 恐慌情绪部分达不到传播阈值时各类人群比例变化图

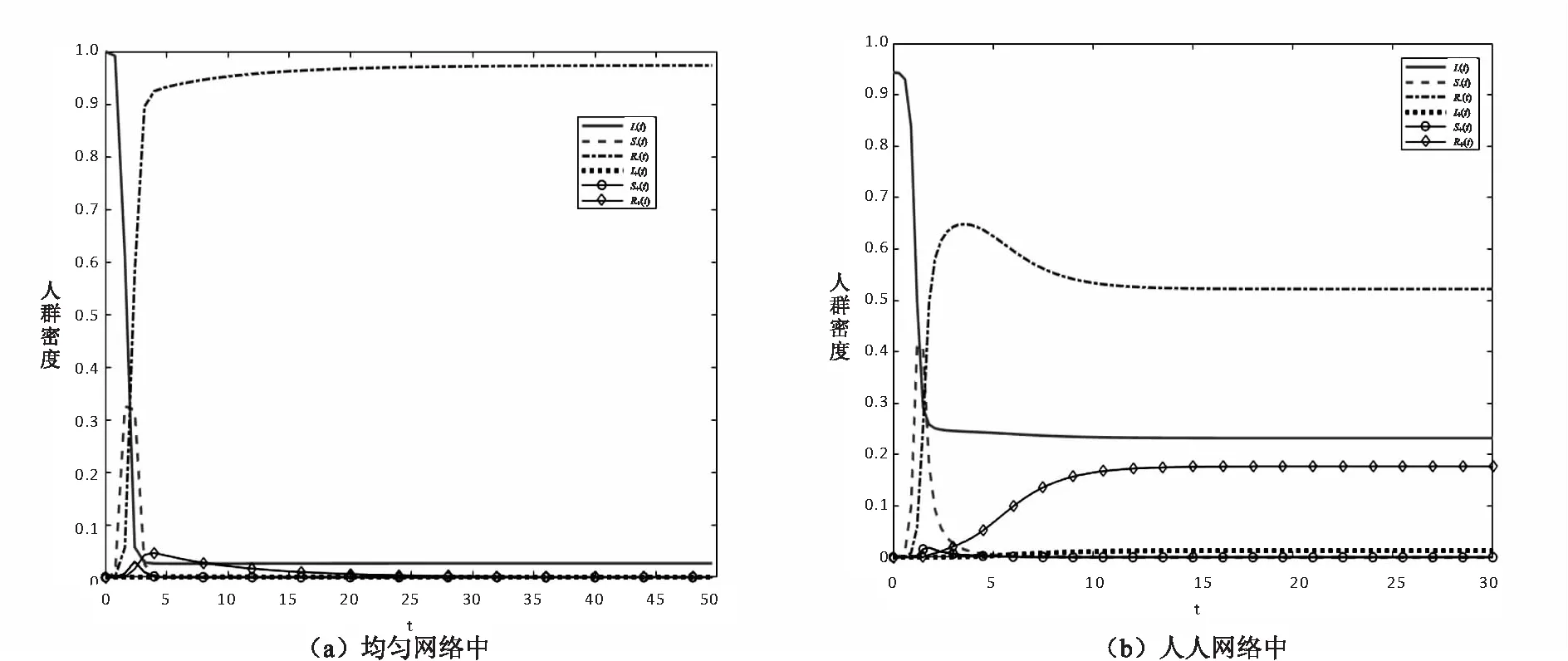
图4 恐慌情绪全部达不到传播阈值时各类人群比例变化图

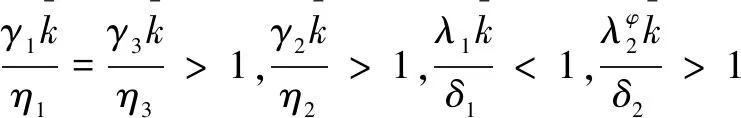
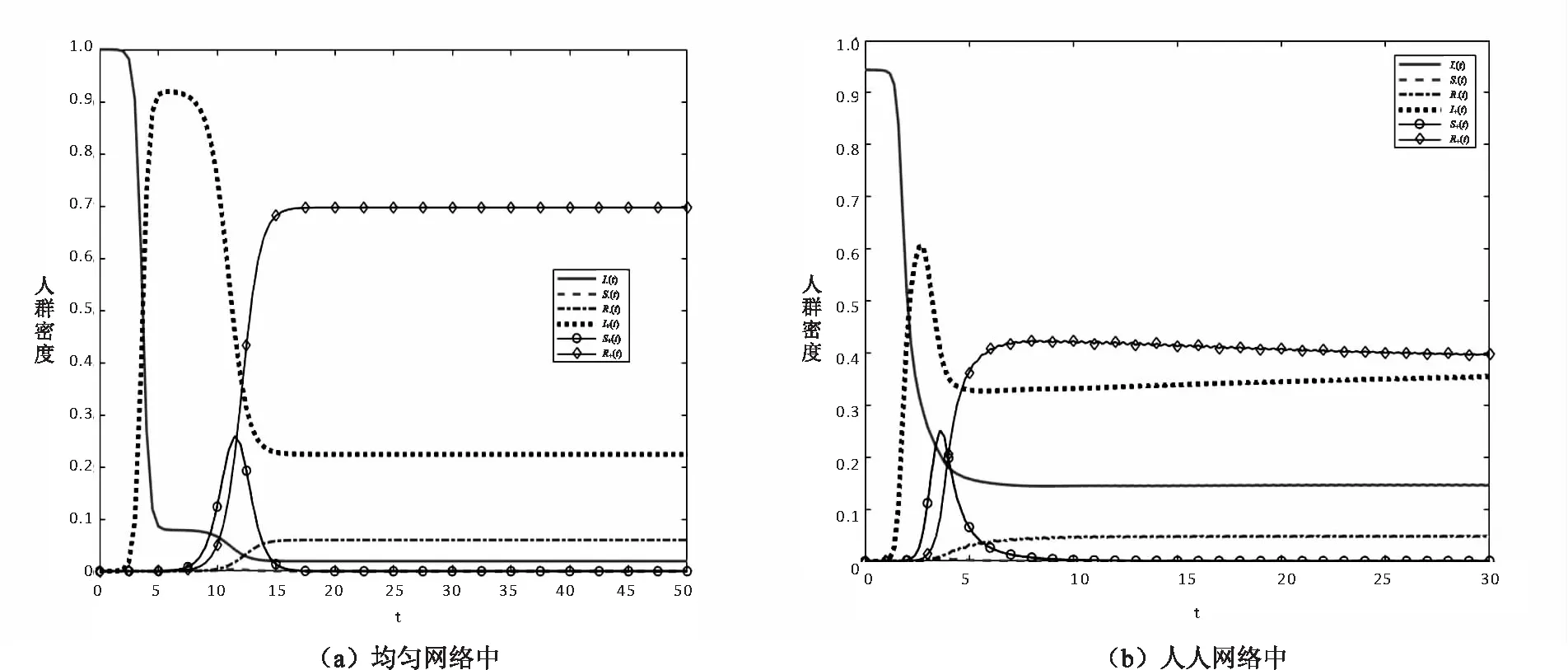
图5 谣言部分达不到传播阈值时各类人群比例变化图

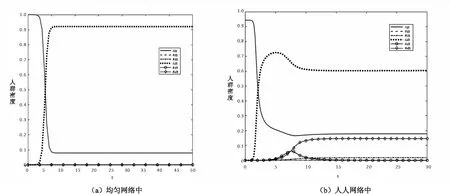
图6 谣言全部达不到传播阈值时各类人群比例变化图

2.3谣言和恐慌情绪双传播的相互影响分析图7和图8分别考察的是在同名转化概率取值相同λ1=λ2=0.3，β1=β2=0.02，δ1=δ2=0.3，α1=α2=0.2，γ1=γ2=γ3=0.2，η1=η2=η3=0.3，θ=0.1和同名转化概率取值不同λ1=0.3，λ2=0.6，β1=0.02，β2=0.01，δ1=0.3，δ2=0.2，α1=0.2，α2=0.1，γ1=γ3=0.2，γ2=0.4，η1=η3=0.3，η2=0.1，θ=0.1时，即谣言和恐慌情绪传播系统独立和关联的情况下，谣言传播和恐慌情绪传播的状态。图7(a)和图8(a)是在均匀网络中进行模拟，图7(b)和图8(b)是在人人网络中进行模拟。图7主要描绘的是恐慌情绪对谣言的影响，图8主要描绘的是谣言对恐慌情绪的影响。图7中的免疫者表示无恐慌免疫者和恐慌免疫者之和，即R(t)=R-(t)+R+(t)，它的终值代表了谣言的传播规模。附图中的传播者表示无恐慌传播者和恐慌传播者之和，即S(t)=S-(t)+S+(t)，它的最高值代表了谣言的最大传播力。从图7中可以看出，无论是在均匀网络还是在人人网中，同名转化率不同的情况下谣言的传播规模及谣言的最大传播力比同名转化率相同的情况下均变大。同名转化概率的取值不同表达谣言和恐慌情绪的相互影响，那么就可以得出恐慌情绪促进了谣言传播的结论。因为人群中的恐慌情绪增大了谣言的传播率，减小了谣言的停止率，谣言在持有恐慌情绪的传播者中传播，传播的力度更大。图8中的恐慌情绪者表示恐慌无知者、恐慌传播者和恐慌免疫者之和，即N+(t)=I+(t)+S+(t)+R+(t)，其中的附图是单把恐慌传播者S+(t)随时间变化的图像描绘出来。从图8中可以看出，无论在均为网络还是人人网中，同名转化率不同的情况使得恐慌情绪持有者的人数变多，直到稳定状态时恐慌情绪持有者的人数变为与同名转化率相同情况下的人数相当。传播过程中，人数多出的部分是由于同名转化率不同时恐慌传播者S+(t)密度大于同名转化率相同时的恐慌传播者密度(见图8)。谣言的传播增大了传播者恐慌率，减小了传播者恢复率，所以谣言使得恐慌情绪持有者的人数高于或等于无谣言时的数量，可以说一定程度上谣言也促进了恐慌情绪的传播。所以，综合图7和图8，可以得出无论在均匀网络中还是现实网络中，谣言和恐慌情绪的传播是相互促进的结论。此结论也与赖胜强等人[17]的实验结论相一致。

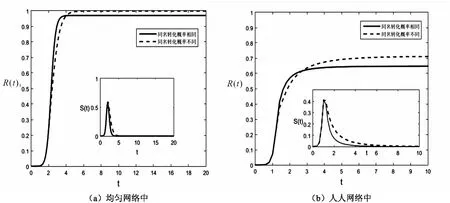
图7 独立和相互影响下的谣言传播

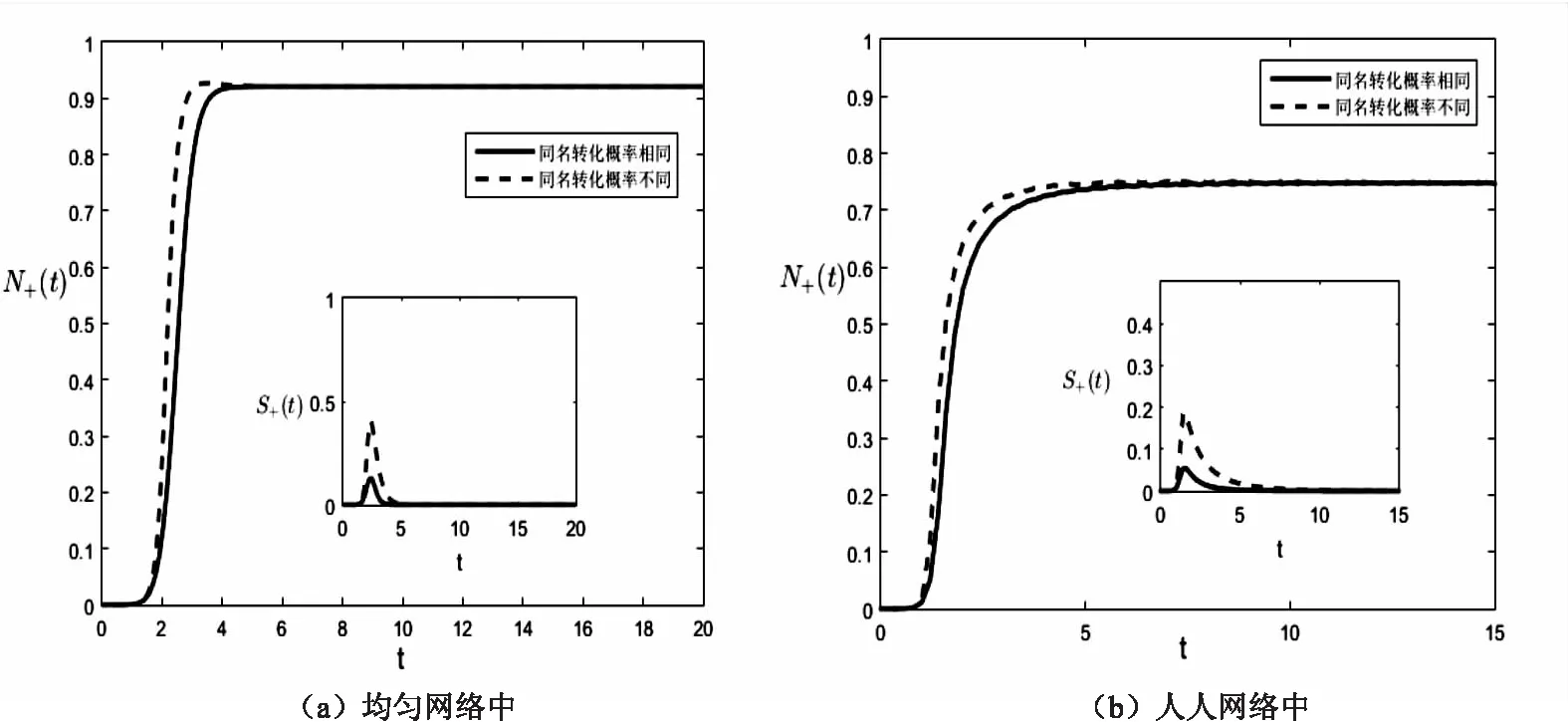
图8 独立和相互影响下的恐慌情绪传播

3 结论及展望

谣言和恐慌情绪往往相伴发生，如果恐慌情绪极化，将会造成比谣言本身更大的危害。考虑到以往谣言传播方面的文章忽略群体情绪，情绪传播方面的文章用谣言代替情绪的传播等问题。本文把谣言和情绪分离开来，区别对待，建立了谣言及恐慌情绪并行传播的双传播模型，模型的建立是对舆情传播理论的内容丰富。通过数学方法，计算出双传播模型独立系统的传播阈值。通过仿真模拟方法，在均匀网络及人人网中分析了双传播模型关联系统传播阈值的变化特征。仿真结果表明，关联系统中，如果谣言(恐慌情绪)达到传播阈值后，那么与之相对应的恐慌情绪(谣言)的传播阈值会降低，尤其是在现实网络中这一特征表现的更为明显。通过仿真还发现，无论在均匀网络还是人人网中，谣言和恐慌情绪的并行传播对彼此具有相互促进的作用，恐慌情绪的产生使谣言波及的范围变广，影响力变大，谣言的传播也加剧了恐慌情绪的传播。本文虽然依托现实网络人人网，用仿真模拟的方法分析了谣言和恐慌情绪的传播阈值变化特征及影响规律，但还是偏重于理论方面的研究，怎样选取合适的案例进行谣言和恐慌情绪双传播的验证将是下一步要进行的工作。