贴坡式玄武岩纤维石笼河道护坡的离散元分析
2021-04-29戴健健马煜钧
戴健健,叶 楠,苏 超,张 恒,祝 凡,马煜钧
(1.河海大学水利水电学院,南京210098;2.吉林水利科学研究院,长春130022)
0 引 言
河道边坡作为河流生态系统的重要组成部分,是河流与陆地生态系统之间的过渡带,在水土保持、净化水体、防洪泄洪等方面具有重要的功能[1]。目前,河道护坡主要分为传统护坡和生态护坡,生态防护技术的诞生顺应人与自然共生的要求,提升了护坡工程建设的内涵[2]。河道护坡材料主要有混凝土、砌石、石笼、土工植物袋和草皮等五种,例如南水北调中线干渠采用植草护坡[3]、三峡水库消落带采用生态袋护坡技术[4]等。对于苏打盐碱土地区的河道,盐碱土会对植物生长造成抑制作用且易腐蚀混凝土和筋材,这给生态防护技术带来了巨大的挑战。玄武岩纤维是一种用天然玄武岩拉制的连续纤维材料,具有强度高、耐腐蚀[5]的优异性能,此外废弃后可在环境中降解。采用玄武岩纤维浇筑而成的复合筋作为石笼结构的网箱,不仅发挥了玄武岩纤维的优良性能,而且可很好地结合石笼结构环境适应性强、整体性好以及施工简便等优点,然而目前鲜有关于玄武岩纤维石笼结构支护方面的研究。因此,将玄武岩纤维石笼结构用于盐碱土河道边坡的支护具有重要的实践意义和学术价值。
石笼网箱内填充的块石作为一种典型的散体,采用连续介质数值方法难以模拟散体结构的力学特性,而颗粒离散元[6]通过圆盘或球体来模拟块石,可以很好地体现散体的力学特性。目前石笼支护结构的数值模拟主要集中在挡土墙方面[7-9],针对玄武岩纤维石笼用于河道护坡的研究较少,迫切需要相应研究来填补该技术领域的空白。本文结合某苏打盐碱土河道护坡工程,采用颗粒离散元PFC2D程序,首先标定土体和玄武岩纤维石笼的细观参数,建立了离散元计算模型。其次考虑河道水流的渗流作用,为更好地对比石笼的支护效果,采用颗粒流强度折减法模拟了设计洪水位下原始边坡的破坏形态。最后从变形和应力两个角度分析玄武岩纤维石笼护坡的稳定性,并研究了玄武岩纤维复合筋的受力特征。
1 玄武岩纤维石笼河道护坡断面型式
某苏打盐碱土河道存在溶陷、渗漏,水土流失等问题。为实现就地取材,节能环保和降低工程造价目的,采用玄武岩纤维生态防护技术对河道边坡进行支护。该边坡支护方案为:坡脚位置放置1 个玄武岩纤维复合筋石笼,尺寸为1 m×1 m×1 m,坡脚左侧位置放置2 个玄武岩纤维格栅护垫,尺寸为2 m×1 m×0.3 m(长×宽×高),坡面贴坡式布置玄武岩纤维格栅护垫,石笼网箱内填充块石,其示意图见图1。根据相应设计资料,表1为该玄武岩纤维石笼护坡的力学参数。
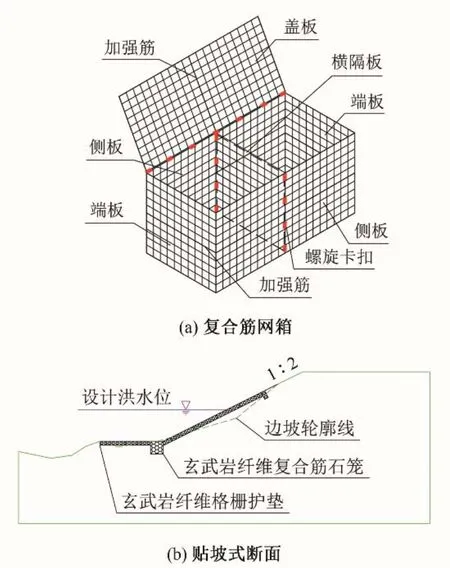
图1 玄武岩纤维石笼护坡Fig.1 Basalt fiber gabion slope protection

表1 玄武岩纤维石笼护坡的力学参数Tab.1 Mechanical parameters of basalt fiber gabion slope protection
2 细观参数标定及离散元模型
2.1 土体和石笼细观参数标定
采用PFC2D程序对土体进行双轴压缩试验标定其细观参数,土体双轴压缩试验的模型尺寸为3.0 m×1.5 m(高×宽)如图2(a)所示。土体颗粒采用接触黏结模型[10],该模型能真实地反映黏土类黏性材料的宏观力学特性。采用试错法最终确定土体的细观参数见表2,100、200、300 kPa 三个不同的围压下土体试样的峰值强度分别为206.32、379.12、543.48 kPa,其应力-应变曲线见图2(b)。通过Matlab 回归分析可求得土体的凝聚力为15.08 kPa,内摩擦角为14.79°,与土体的力学参数吻合得很好。

图2 土体细观参数标定Fig.2 Calibration of soil micro-parameters

表2 土体颗粒的细观参数Tab.2 Micro-parameters of soil particles
目前采用实际工程尺寸的室内和现场石笼试验研究较少,因此,以蒋洋等[11]做的石笼单体单轴压缩试验作为参考(试样尺寸为0.5 m×0.5 m×0.4 m),建立单轴压缩试验的石笼尺寸为1 m×0.5 m。复合筋网箱中填充的块石采用线性模型,玄武岩纤维复合筋采用平行黏结模型以模拟其受拉和受弯特性。采用试错法确定石笼的细观参数见表3,模拟的应力-应变曲线与文献[11]室内试验C1试样结果对比如图3所示,可见标定的细观参数能够合理地反映石笼的力学特性。

表3 玄武岩纤维石笼细观参数Tab.3 Micro-parameters of basalt fiber gabion
2.2 玄武岩纤维石笼护坡离散元模型
采用PFC2D程序与AutoCAD 相结合的方法建立石笼护坡土体部分,运用geometry import 与wall import geometry 命令将dxf格式文件导入生成边坡的轮廓与墙体,运用ball distribute 命令生成土体颗粒,在模型达到平衡状态后进行颗粒速度和位移的清零,赋予土体颗粒表2的细观参数。玄武岩纤维石笼采用编写的FISH 函数生成,该函数可生成采用颗粒黏结的任意线段,对于任何的玄武岩纤维复合筋网箱,只需输入四条边起点和终点坐标。生成的石笼模型如图4(a)所示,计算区域取坡顶向右延伸10 m和坡高12 m,最终建立的玄武岩纤维石笼护坡离散元模型如图4(b)所示。该模型颗粒总数为131 509 个,其中土体颗粒121 253个,块石颗粒563个,玄武岩纤维复合筋颗粒9 693个,土体与石笼间以及石笼单体间的接触均采用线性接触模型,其细观参数见表4所示。由坡顶至坡脚分别在石笼护坡的4个不同位置设置半径为1.0 m 的测量圆,记录相应位置土体颗粒在坡体滑动过程中应力的变化情况。此外为更好地对比石笼的支护效果,同时建立原始边坡的离散元模型如图5所示,土体颗粒共120 637个。

图4 玄武岩纤维石笼护坡离散元模型Fig.4 Discrete element model of basalt fiber gabion slope protection
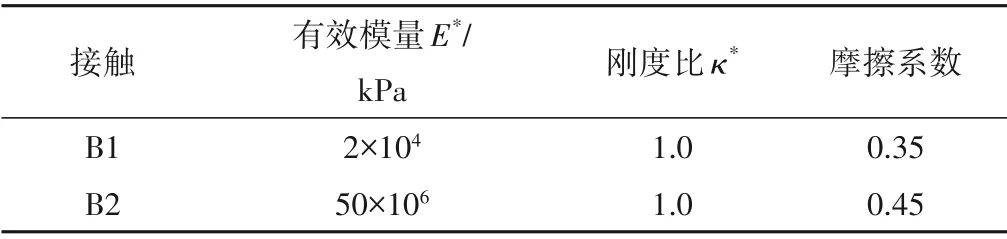
表4 石笼界面的细观参数Tab.4 Micro-parameters of the stone cage interface

图5 原始边坡离散元模型Fig.5 Discrete element model of the initial slope
3 玄武岩纤维石笼护坡离散元分析
3.1 渗流作用的模拟
考虑到PFC2D中无内置的渗流计算程序,因此采用简化方式考虑渗流作用的影响。渗流作用简化计算的基本思路为:①采用有限元计算边坡在相应水位的渗流场;②导出单元节点的水力梯度,计算单位渗透体力;③以有限元网格节点为圆心,网格的平均尺寸为半径作圆;④将全部有限元网格节点对所有土体颗粒循环,若土体颗粒圆心在圆内,则将渗透体力通过PFC内置函数施加到土体颗粒上。此外由于在水位线以下的颗粒受到浮力作用,浸润线以下土体颗粒的重度采用浮重度。
为减小边界的影响,有限元渗流计算域取坡顶向右延伸100 m和坡高25 m。设计洪水位下玄武岩纤维石笼护坡和原始边坡的总水头和浸润线如图6所示。
3.2 原始边坡稳定性分析
颗粒离散元强度折减法[12]的基本思路为将颗粒的法向、切向黏结强度和摩擦系数同时进行折减,其公式如下:

式中:Fs为滑坡的稳定系数;cbtenf为颗粒的法向黏结力;cbshearf为颗粒的切向黏结力;fric为颗粒间的摩擦系数;cbtenfcr、cbshearfcr和friccr依次为颗粒的临界法向黏结力、切向黏结力和摩擦系数。
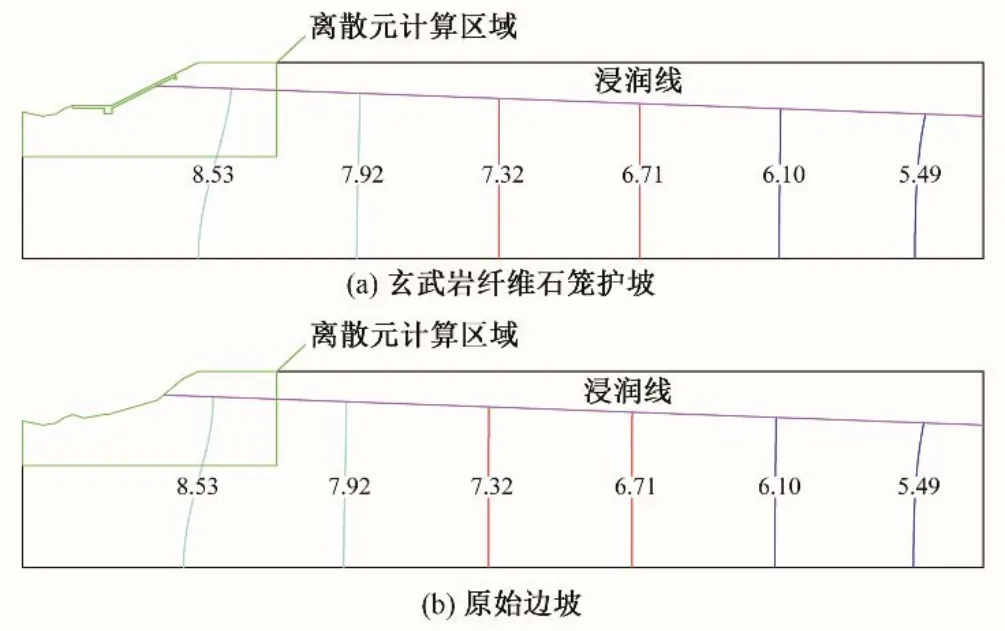
图6 设计洪水位工况的总水头和浸润线(单位:m)Fig.6 The total head and wetting line for design flood level conditions
为更好地对石笼支护效果进行分析,首先对原始边坡的滑坡破坏形态进行模拟,根据文献[12]的判定准则求得原始边坡稳定系数为2.20。对土体颗粒的法向、切向黏结强度和摩擦系数同时折减2.20 倍,对边坡施加重力和渗透体力进行滑坡破坏模拟,计算时步取100万步。在重力和渗透体力作用下,坡脚处颗粒首先发生挤压破坏变形加剧,坡内颗粒接触黏结断裂形态向圆弧形式发展,土体发生剪切破坏。30万步时断裂的接触黏结贯穿坡顶,贯通面形成,坡顶失去支撑的作用。50 万步时坡顶产生明显张拉裂缝,坡体发生失稳破坏,沿贯通的圆弧式断裂黏结滑移,见图7(b)。随着时间的推移,断裂的接触黏结继续发展,破坏的坡体继续下滑,70 万步时滑坡体颗粒间部分黏结破坏,出现二次破坏,由于土体具有一定凝聚力,滑坡体在一些局部位置发生张拉破坏,滑坡体局部破碎,并滑移堆积至坡脚处。100 万步时坡体的滑动面已经呈现出圆弧状,此时滑坡体趋于稳定。
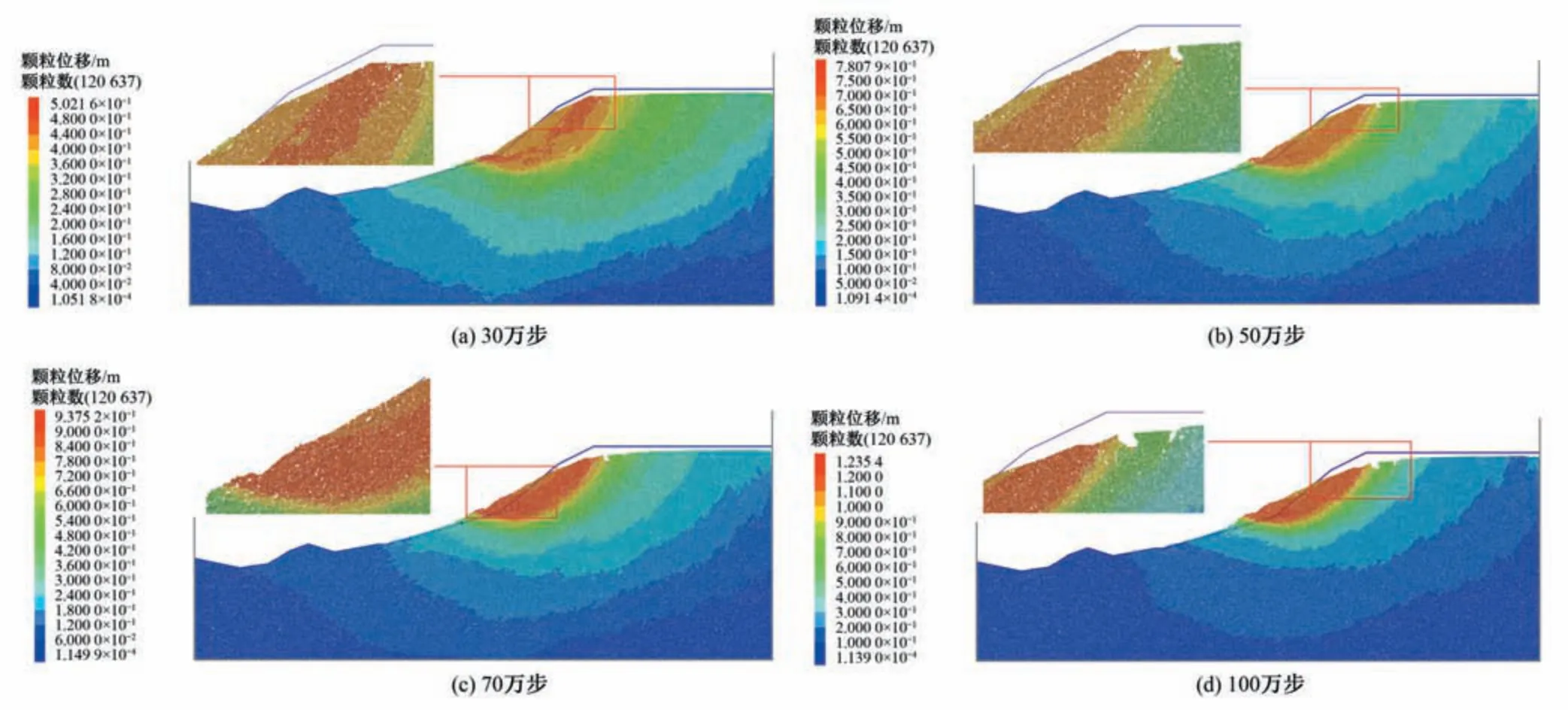
图7 原始边坡滑坡破坏形态Fig.7 Initial slope landslide failure mode
3.3 石笼护坡稳定性分析
对于设计洪水位工况下的玄武岩纤维石笼护坡,对土体颗粒的法向、切向黏结强度和摩擦系数同时折减3.10 倍,对护坡施加重力和渗透体力进行100万步的计算。计算完成时坡内土体颗粒断裂的接触黏结分布均匀,无法形成贯穿的滑动面,玄武岩纤维石笼护坡未发生滑动破坏,表明采用石笼支护可有效提升边坡稳定性并防止坡内土体的破坏和滑动,这对滑坡的防治具有积极意义。由于石笼护坡未发生破坏,可以认为石笼护坡的稳定系数在3.10 以上,从安全角度考虑可取其稳定系数为3.10。
玄武岩纤维石笼护坡的破坏形态主要表现为石笼的错位与复合筋受弯脱开,坡体未发生滑动破坏的原因在于:①由于从坡脚至坡顶均采用石笼进行支护,石笼内填充块石密度为土体密度的1.79 倍,相当于在坡面加了盖重,在石笼重力作用下提升边坡的整体性;②采用石笼支护后,块石与块石间、块石与复合筋间、石笼单体间及石笼与土体间的摩擦作用,这使得土体颗粒接触黏结断裂的分布更加均匀,无法形成贯通的滑动面。
3.3.1 变形特征
对于玄武岩纤维石笼护坡,40 万步时,在重力和渗透体力作用下,土体颗粒位移从底部逐渐向坡顶处发展,石笼在块石颗粒和土颗粒的共同作用下,玄武岩复合筋产生受弯变形,见图8(a)。60 万步时,位移向坡内中部发展,由于周围土体颗粒的挤压作用,位于坡脚左侧的玄武岩纤维石笼网箱的位置发生错动,如图8(b)所示。80万步时,位移向坡顶处发展,由于周围土体颗粒发生沉降,石笼单体的复合筋网箱受弯,如图8(c)所示。100万步时,坡内土体的位移发展基本完成,坡顶位置位移最大,石笼单体之间出现脱离分开现象[图8(d)],坡内土体颗粒断裂的接触黏结分布均匀,无法形成贯穿滑动面,因此石笼护坡未发生滑动破坏。

图8 玄武岩纤维石笼护坡变形特征Fig.8 Deformation characteristics of of basalt fiber gabion slope protection
3.3.2 应力特征
图9为玄武岩纤维石笼护坡在计算过程中记录的应力变化曲线,4 个测量圆在计算初期一定的时步x方向和y方向的应力基本为零,这是由于土体颗粒位移是从坡脚逐渐向坡顶发展,位移发展过程需要一定时间,在建立石笼护坡模型时土体颗粒已经达到平衡,其接触力趋于零,因此测量圆得到的应力基本为零。测量圆1 的位置靠近坡顶,测量圆4 的位置靠近坡脚,因此1 号测量圆x方向和y方向的应力基本为零的时间最长,4 号测量圆的最短。随着时间的推移,在坡脚左侧与坡面石笼单体重力的作用下,土体颗粒紧密接触,记录的x方向和y方向应力增大。测量圆的y方向应力比x方向大,这是由于在石笼支护作用下,坡内土体颗粒断裂的接触黏结无法形成贯穿的滑动面,土体颗粒受到自身重力、渗透体力以及石笼重力的作用导致。
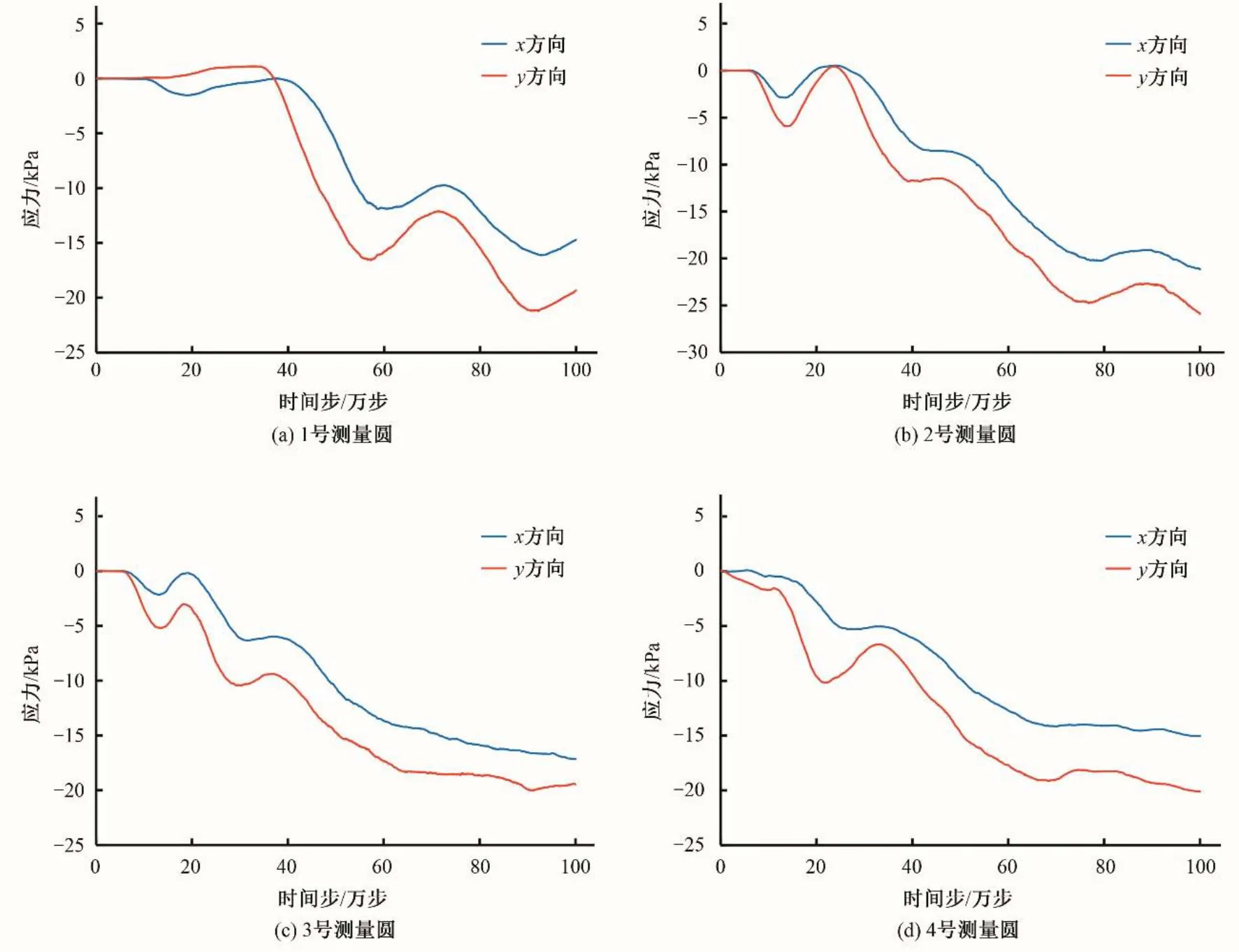
图9 玄武岩纤维石笼护坡应力特征Fig.9 Stress characteristics of basalt fiber gabion slope protection
3.3.3 玄武岩纤维复合筋受力特征
玄武岩纤维复合筋的受力状态如图10所示,蓝色表示受压,绿色为受拉。坡面贴坡式布置的1 m×2 m×0.5 m(L×W×H)型石笼在重力和渗透体力作用下底部复合筋呈现受压状态,坡面中间两个石笼顶部复合筋受拉。坡顶处石笼复合筋受力状态为受拉,坡脚左侧的两个玄武岩纤维格栅护垫在土体颗粒及坡面石笼的作用下主要处于受压状态。玄武岩纤维复合筋的最大应力为压应力其大小为8.27 kPa,出现在坡面第1 个玄武岩纤维格栅护垫底部中间偏下位置,复合筋的拉压应力远低于其允许的强度值。从安全的角度考虑,建议靠近坡脚位置的石笼网箱采用直径更粗的复合筋或增加网箱间卡扣的数量。
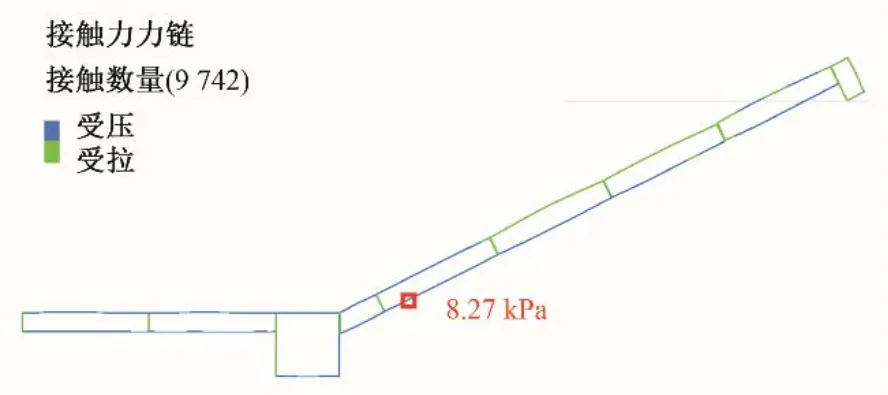
图10 玄武岩纤维复合筋受力状态Fig.10 Stress state of basalt fiber composite bars
4 结 论
(1)盐碱土河道边坡采用玄武岩纤维石笼支护可以充分发挥玄武岩纤维和石笼结构的优点,计算表明在设计洪水位下护坡的稳定系数较原始边坡提升了40.9%,采用石笼支护后坡内土体未发生破坏和滑动。
(2)玄武岩纤维石笼护坡的破坏形态主要表现为石笼的错位与复合筋受弯脱开,采用石笼支护相当于在河道坡面增加盖重,加上石笼之间及石笼与土体间的摩擦作用使得边坡稳定性得到提升,坡内土体颗粒断裂的接触黏结分布均匀,无法形成贯穿的滑动面。
(3)玄武岩纤维复合筋的受力状态既存在受拉也存在受压,与土体接触的复合筋受压为主而坡面的受拉为主,复合筋拉压应力远低于其允许的强度值。 □
