考虑多种气候指数的淮河流域气象干旱预测

纪昌明，马皓宇，彭 杨，李宁宁

（华北电力大学水利与水电工程学院，北京102206）

0 引 言

近几十年随着全球气候变暖与极端气候事件增多，干旱在频率、强度和持续时间方面均有增强的趋势［1］，其对农业、城市供水和生态系统等造成巨大威胁，美国每年因干旱损失60～80亿美元，远超其他种类的气象灾害。然而与洪水、台风和地震等灾害不同，干旱是缓慢演变的，故可利用从干旱发生到其对农业生产和供水产生影响的时间差，采取一系列措施以减轻损失。而干旱预测的准确性则直接影响抗旱策略的制定与实施，不同学者提出一系列预测方法：以地表模拟模型为基础，Shef⁃field［2］建立了撒哈拉以南非洲地区的试验性干旱监测与预报系统；Hao［3］通过全球干旱综合监测预报系统对全球范围内的几次重大干旱进行分析，验证了该系统能有效地捕捉干旱的发展；Deo［4］通过多元自适应回归、支持向量机和M5Tree 模型，预测澳大利亚东部的SPI变化。

本文的研究内容是已知当前干旱状态，计算转移至未来某一等级干旱的概率，之前大多利用马尔可夫链实现，而Cancel⁃liere［5］指出了该方法进行概率预测的不足，即转移概率的计算存在明显偏差，直接计算所得的多步转移概率矩阵与基于马尔科夫假设由单步矩阵推得的多步矩阵之间存在显著差异，并指出通过极大似然法估算转移概率可能得出错误结论。为避免上述问题，本文利用SPEI 指数表征干旱状态，通过R-vine Cop⁃ula描述预报模型中的多维变量的联合分布，并使用概率积分变换（PIT）直接计算1-3月后的干旱转移概率。目前常利用的阿基米德或椭圆Copula 在高维情况下均具有较大的局限性，而R-vine Copula 可将高维Copula 分解为若干二元Copula，且二元Copula的类型不受限，故能灵活且方便地构建高维联合分布。

此外，ENSO 等海气相互作用对区域气候的影响也得到证实，目前尝试将其作为预报因子以提升干旱转移的预报精度。然而干旱通常受多种气候因素的调节，目前干旱转移的研究仅考虑一种指数的影响［6，7］，且多元联合分布的建立具有局限性，故本文同时考虑多种指数的影响，选择R-vine Copula 准确构建多维变量的相关结构。选择淮河流域作为研究区，选择ENSO、ENSO Modoki、NAO、IOD 和AO，在概率预报模型中考虑多种指数的影响，以改善淮河流域内干旱转移预报精度，类似的研究尚未在淮河流域开展。

1 材料与方法

1.1 数据来源

本文将淮河流域内36 个气象站点的1977-2017年的降水量、温度、相对湿度、风速、日照时数和地表气压的日气象数据，作为SPEI指标的输入，数据来源于中国气象局国家气象信息中心，站点分布如图1所示，缺失数据利用其他年份该日的平均值填充。

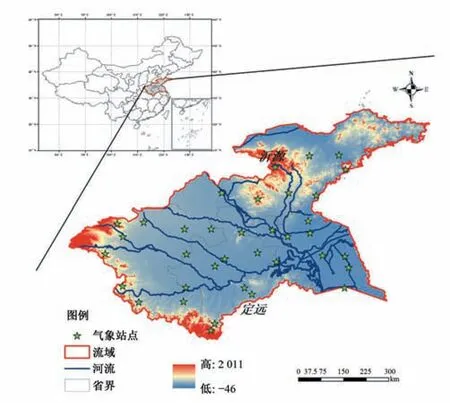
图1 研究区域和气象站点分布Fig.1 Study region and spatial distribution of meteorological stations

淮河流域内气候变化与一系列大尺度气候因子存在遥相关，选择ENSO、ENSO Modoki、NAO、IOD 和AO 这5 种大气环流模态，挑选相应指数来表征其强度变化。选择Niño3 指数表征ENSO，其定义为Niño 3 区的海表温度距平值；EMI 指数表示中部型ENSO 的强度［8］；NAO 指数为直布罗陀和冰岛西南部的标准海平面气压差；DMI指数表示IOD强度，定义为西印度洋与东印度洋的海温距平之差；AO 指数为对北半球热带外海平面气压距平的经验正交函数分析第一模态时间系数。

1.2 SPEI干旱指数

SPEI 由Vicente-Serrano［9］提出并用于干旱监测，其同时考虑降水量和潜在蒸发量这两个因素，可以反映气候变暖背景下的干旱情况。SPEI的时间尺度通常为1、3和12个月，用于监测月、季以及年尺度的气象干旱，淮河流域以季节性干旱为主，故选择3 个月的时间尺度（SPEI-3）。使用Xiao［7］中提供的SPEI干旱分类表，如表1所示。

表1 基于SPEI的干旱等级划分Tab.1 Drought classification based on SPEI values

1.3 R-vine Copula函数

较多元正态分布，Copula 函数可以模拟非正态分布下的相关性结构，对变量边际分布的类型无限制，因此在统计分析上得到广泛应用。Archimedean Copula 和Elliptical Copula 是常用Copula 的类型，但其要求变量间的相关结构相同，故无法准确描述较高维变量间的依赖关系。R-vine Copula 则克服了上述问题［10，11］，作为一种基于Pair Copula Construction（PCC）的图论模型，能自由选择2维Copula函数类型，使得多维变量联合分布的建立极具灵活性。在确定藤结构与各个变量的边缘密度函数后，可将d维概率密度分解为d（d-1）/2 个2 维Copula 密度函数的组合，极大简化了高维相关性结构的构建难度。

1.4 转移概率计算

因观测样本的局限性，基于极大似然法计算转移概率受到较多学者的质疑［5-7］。为此本文利用1.3 节介绍的R-vine Copu⁃la，构建反映预报因子与预报量间相关关系的关联结构，接着在已知预报因子准确值的条件下，计算预报量处于不同范围的概率。令Z0表示当前月份的SPEI-3，W1，…，Wd-2表示当前月份的（d-2）个气候指数，Z1表示未来月份的SPEI-3，u1，…，ud表示变量的边缘分布，其中u1和ud表示Z0和Z1的边缘分布，令C表示利用观测样本构建的R-vine Copula，利用下式通过条件Copula计算条件概率值：

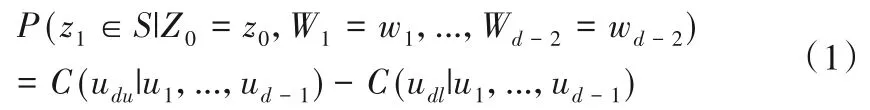
式中：Z1的范围S=［sl，su］，相应的边缘分布udl=Fd（sl）和udu=Fd（su）。C（ud|u1，…，ud-1）为条件Copula，通过PIT计算获得，详细的求解方法见参考文献［12］。

本文利用“VineCopula”包中的函数“RVinePIT”，输入多维变量边缘分布值的数据集，将PIT 应用于已建立的R-vine Copula模型，由此预测未来不同干旱状态的条件概率。

2 结果与分析

2.1 相关关系分析

淮河流域气候条件复杂且不同区域间的差异较大，选取旱灾频发的山东和安徽的气象站点进行重点分析：站号54836 的山东沂源站和站号58225 的安徽定远站。计算站点的SPEI-3序列。接着确定预报所需的潜在预报因子，利用Pearson相关系数，分析站点各月的SPEI-3 与之前1-3月的气候指数间的关系，以识别两者间的滞后相关。气候指数按1，3，12月取滑动平均值，并进行标准化，滞时lag为指数滑动平均期（AP）的结束月与SPEI所在月间的时长。图2展示SPEI-3 与气候指数序列间相关分析结果，通过热点图展示不同气候指数（行）、滑动平均期（列）、月份（x轴）和滞时（y轴）组合下，气候指数与SPEI-3间相关系数，数字表示通过5%显著性水平的双边t检验。

对沂源站，因篇幅限制，仅展示SPEI与NAO、IOD和AO的相关结果，如图2（a）所示。淮河流域的山东部分易发生冬旱，1月SPEI-3 可表示冬旱程度，故重点研究1月情况。可以看到11、12月的NAO（AP=1，3，12月）与1月的SPEI-3 呈现出显著的正相关，10、11月的IOD（AP=1，3月）以及12月的IOD（AP=3，12月）与SPEI-3显著相关，10、11和12月的AO（AP=12月）与SPEI-3 显著相关。对定远站，选取Nino3 和EMI两个指数的相关系数展示，如图2（b）所示。定远站位于江淮分水岭区域，较其他地区更易形成春旱，通过5月的SPEI-3值可体现春旱的严重程度，故将5月作为典型月份。可以看出2、3月的Nino3（AP=1，3，12月）以及4月的Nino3（AP=3，12月）与5月的SPEI-3 呈现显著的正相关，2、3 和4月的EMI（AP=1，3，12月）与SPEI-3均呈现显著相关。

沂源站的冬季气候受东亚冬季风的支配，NAO、IOD 和AO通过影响西伯利亚高压和阿留申低压进而影响东亚冬季风的强度，从而对区域的气温、降水等造成显著影响［13-15］。定远站的结果与Zhang［16］的结论一致，即由传统ENSO 和ENSO Modoki 定义的海表温度异常升高会导致淮河流域的春季降雨明显增加，从而提高SPEI。

2.2 选择预报因子

在干旱转移的预报中，将与未来SPEI显著相关的不同滑动平均期的不同指数作为潜在的预报因子，但把所有指数都作为预报因子，预报结果通常并不理想，原因在于指数间几乎总是相互关联的，所有指数的完整集合通常包含较多的冗余信息，导致预报效果无法提升甚至劣化。因此需筛选预报因子，确定模型合适的输入，此处使用统计预报中常用的筛选方法—逐步引入，注意与指数同月份的SPEI-3作为默认预报因子。

概率预报的评价采用留一交叉验证，评价指标选择分级概率评分RPS，通过1977-2017年留一交叉验证的RPS均值评价SPEI多分类概率预报的精度。表2展示预报模型在2个站点上的应用效果，开始仅使用当前月份的SPEI-3 作为预报因子，接着将逐步引入所确定的最佳因子集内的元素逐个加入。粗体表示当前的RPS序列与之前有显著差异。由表2可以看出，随气候指数的逐个加入，其包含的遥相关信息有助于提升预报精度，且相比于仅使用单个指数，多个指数的同时引入效果更佳，由此证实了Bonaccorso［6］与Xiao［7］在其文章结论处的想法：应根据区域的气候特征选择一系列的大尺度气候指数，将其作为预报因子以提升干旱等级预报的精度。所列站点的最佳因子集通常仅包含5 类指数中的2 类，说明没有必要同时引入过多指数。观察同一站点不同滞时的RPS均值，可以看出该值随预见期的增长而增加，这与大多数预报方法相一致，即预报精度随预见期的增长而降低。

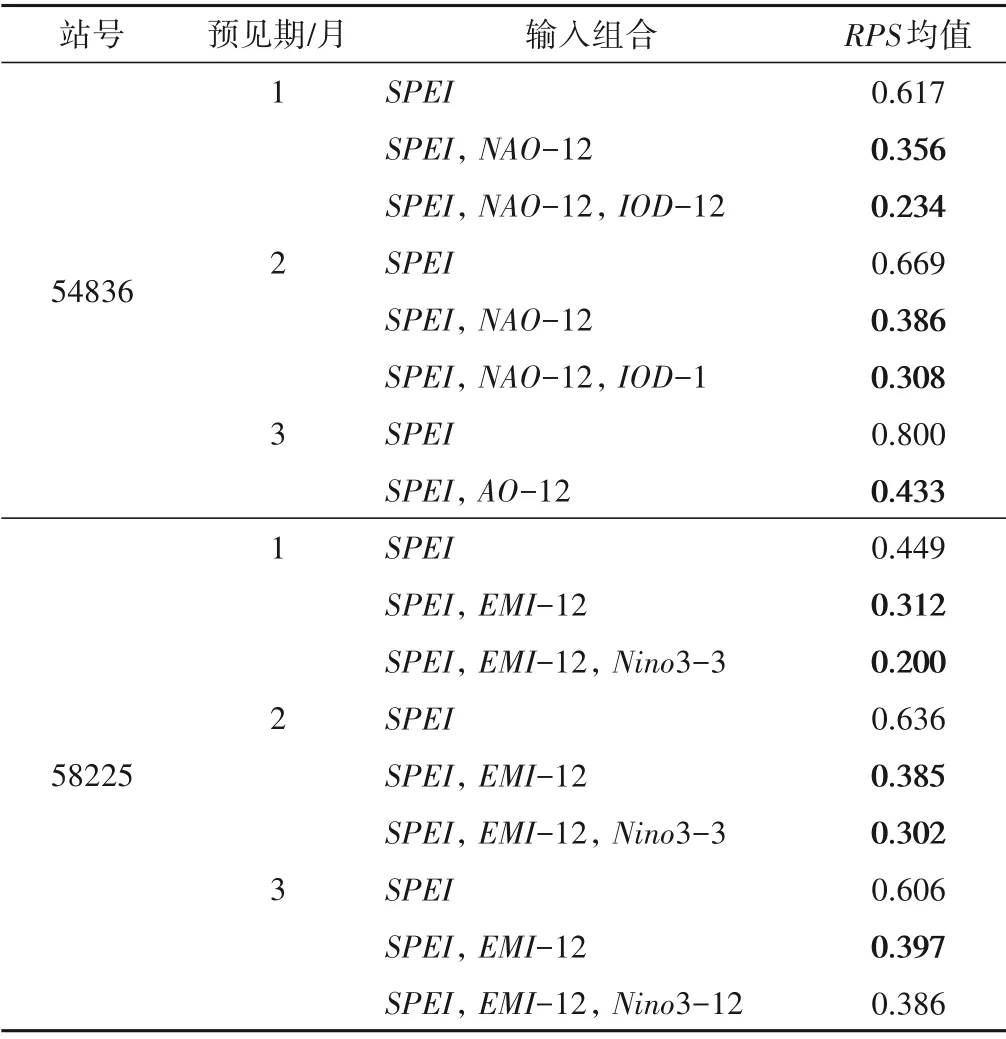
表2 输入组合对预报效果的影响Tab.2 Influence of different input combinations on forecasting

2.3 气候指数对转移概率的影响

在上节获取最佳因子集后，本节计算当前月各个指数处于不同值时，由当前不同的干旱状态转移至未来不同状态的转移概率。图3展示对沂源站1月SPEI-3 的转移概率，12月的NAO-12 和IOD-12 两指数的影响，图4表示2月的EMI-12 和Nino3-12 对5月干旱的影响。两图中行表示当前SPEI-3 取不同值，列表示未来不同的干旱状态。同时对于当前SPEI值和未来SPEI等级的每种组合，绘制3 种图：同时考虑当前月的两种气候指数值w1（x轴）和w2（y轴）的转移概率（中部图）；仅考虑指数值w1或w2的转移概率（下侧图和左侧图）。

将3类图进行对比，分析多个指数较单个指数的不同，以第一行第一列为例（z0=-3，未来旱情在重旱及以上）。图3中，大图左侧的一维图随w2的增加，转移至重旱的概率由0.687 降至0.122，下侧图随w1的增加，概率由0.988降至0.047，其变化范围明显大于左侧图，说明当仅考虑单个指数时，NAO对转移概率的影响高于IOD。当同时考虑两者时，对于w1=-3，w2=3 的加入使得概率值由0.988 降至0.481，当w2=-3 时，w1=3 使概率由0.687 降至0.067，由此验证指数对干旱转移的影响是相互调节的。另外由等高线的斜率可以判断指数影响的相对强弱，总的来看，图中等高线接近垂直方向，故未来旱情是否达到重旱以上主要取决于NAO-12。

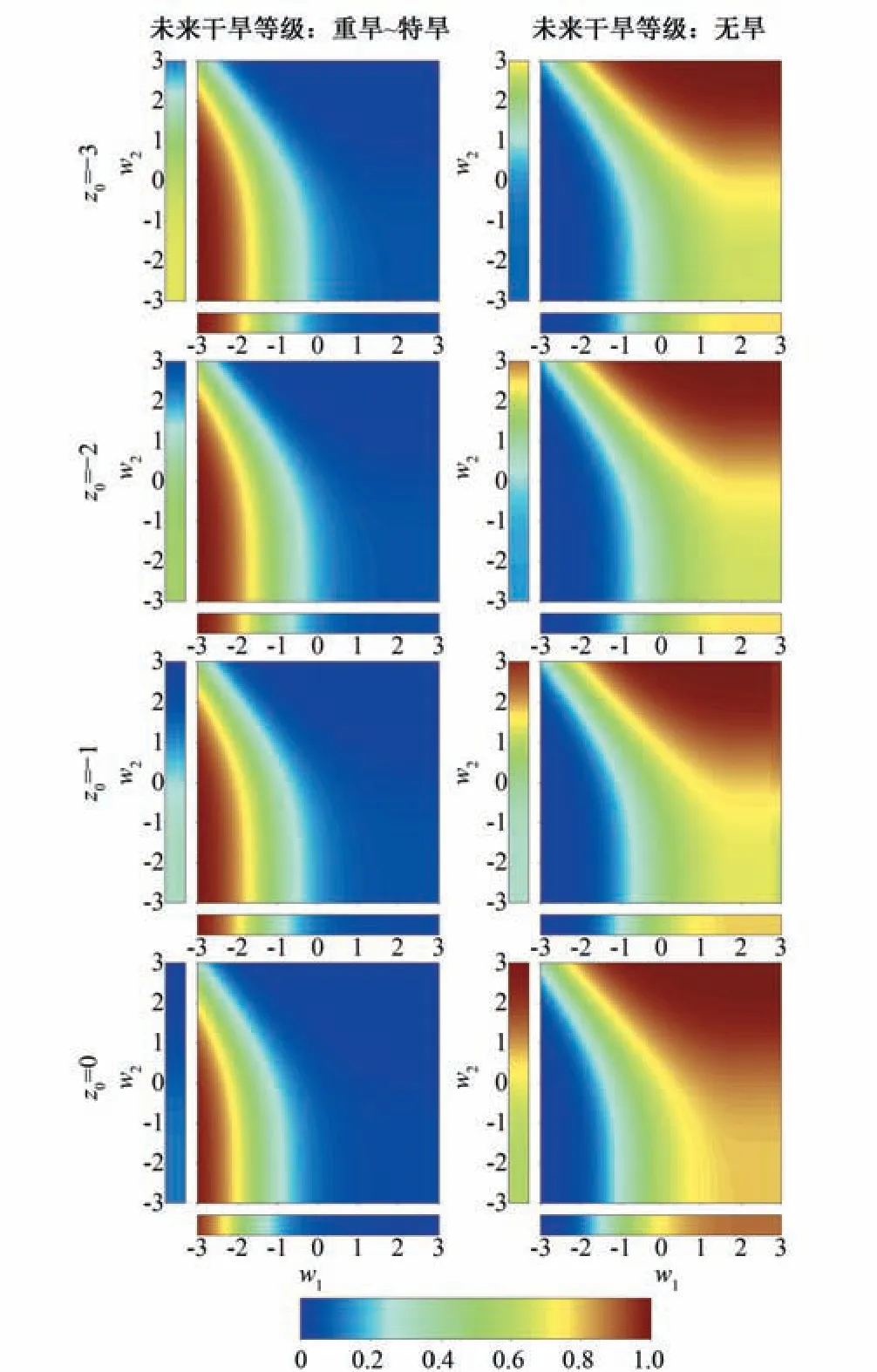
图3 沂源站的转移概率变化图Fig.3 Change of transition probabilities at Yiyuan station

图4中，左侧图中随Nino3-12 的增加，转移概率由0.616 降至0.049，下侧图中随EMI-12 值的增加，概率由0.501 降至0，此时仅由变化范围无法区分两种指数的影响强弱。对于中部图，当w1=-3 时，w2=3 的加入使得概率值由0.501 降至0.319，当w2=-3 时，w1=3 使得概率值由0.616 降至0.06。当w1＜=-2 时，等高线接近水平，说明EMI此时支配概率变化，当w1＞-2，等高线与水平方向形成夹角，说明Nino3的影响增强，但EMI仍是决定重旱发生与否的主要因素。

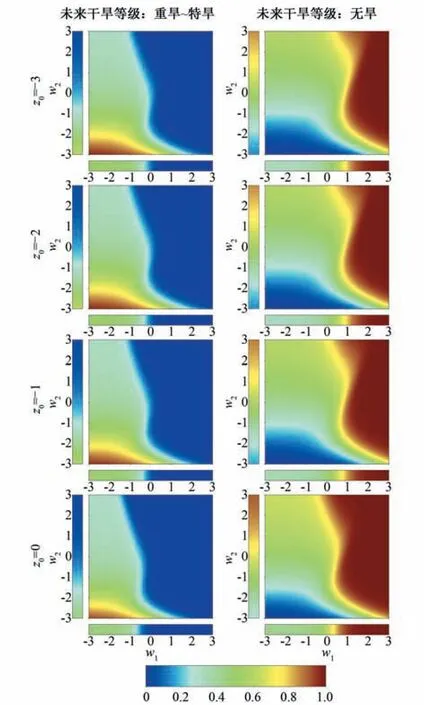
图4 定远站的转移概率变化图Fig.4 Change of transition probabilities at Dingyuan station

2.4 历史干旱转移的概率预测

本节探讨预报模型在实际干旱事件中的预报效果。依据中国气象灾害大典和中国水旱灾害公报，挑选SPEI-3反映的与实际情况相符的典型干旱转移事件，能否准确预测此类事件，对于及时调整水库供水、应急调水等措施极为重要。图5和图6中不同行代表不同年份，左侧标注该年待预测月的干旱等级，不同列对应1-3月的预见期，每个圆环图有两层，内层代表基于当前SPEI值的概率预测结果，外层表示基于当前SPEI和气候指数值的结果，图中心标注出当前SPEI和气候指数的具体值。

图5是针对沂源站1月的SPEI-3，利用表2确定的最佳因子集通过R-vine Copula 进行概率预报：1990年1月是去年下半年持续干旱转变为洪涝的过渡点，在lag=1，2月时，NAO-12 处于极端正值，明显提高了干旱结束的可能，lag=3月时，AO-12高达2.837，使得无旱概率P=0.791；1998-1999年的特大干旱在秋冬季持续，lag=1，2月时，NAO和IOD的值均低于-1，由此推断出极端干旱可能持续（重旱及以上等级的P＞0.6），lag=3月时AO-12 的极端负值使得中旱及以上干旱的P＞0.9；2002年夏秋连旱，而次年暴发洪水，1月成为过渡，lag=1，2，3月涉及的指数均处于正相位，显著提高了无旱的可能；2010-2011年的秋冬季极端干旱持续，lag=1，2月时，NAO-12值低至-3以下，由此成功推断出特旱的暴发和持续（P＞0.8），当lag=3月，AO-12 的极端负值使无旱向极旱以上旱情转移的P＞0.9。

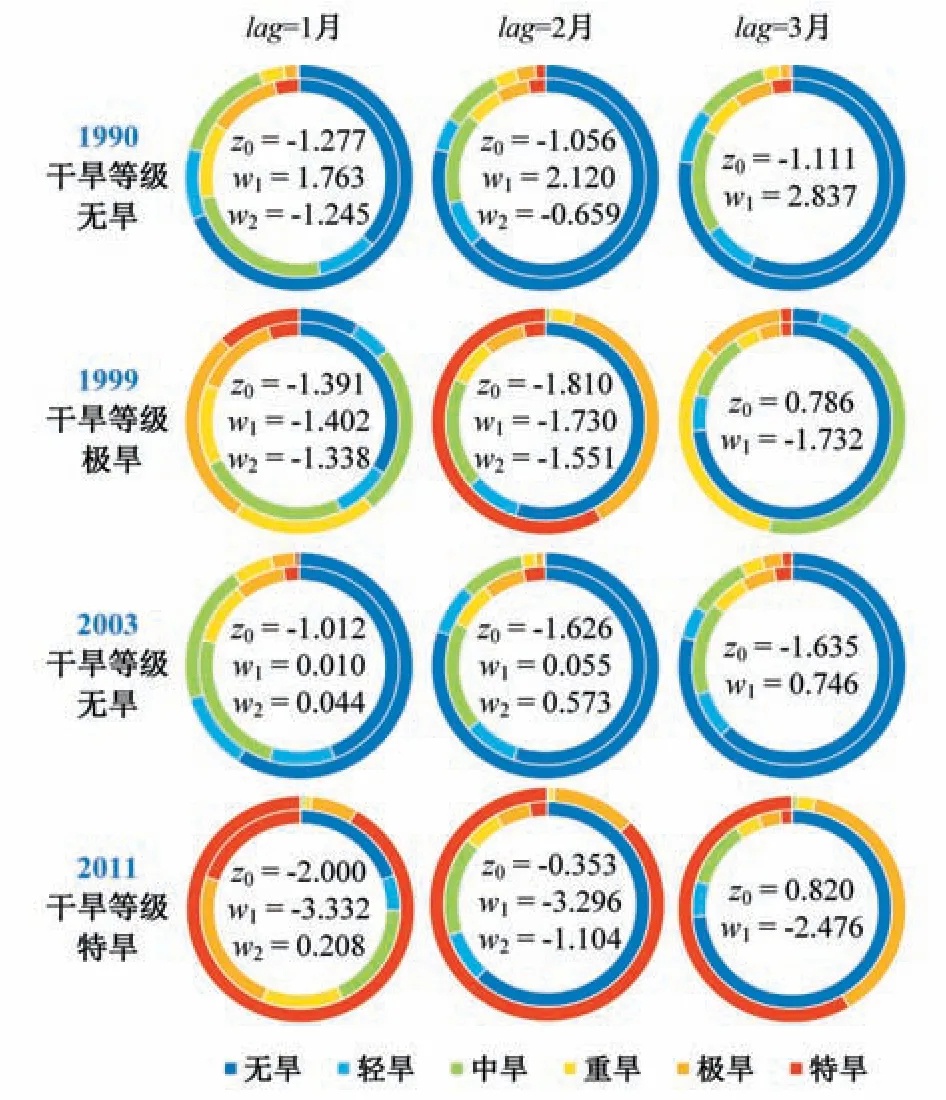
图5 沂源站的历史干旱转移预测Fig.5 Prediction of historical drought transition at Yiyuan station

图6展示定远站5月干旱状态的预报结果：1985-1986年冬春季持续重旱，春末旱情得到缓和，在lag=1，3月时，Nino3指数为负，EMI指数为正，两者共同作用提升了轻中度干旱的发生概率，有利于得出旱情减缓的重要信息；1994- 1995年冬季暴发极端干旱，旱情于春季因强降雨解除，lag=1，2，3月时EMI始终处于极端正值，保证旱情大概率消退；2000年因春季降水不足而发生极端干旱，lag=1月时，气候指数使极旱及以上干旱持续的概率大幅提升，lag=2，3月时，两指数的极端负值保证了重旱及以上干旱的发生概率亦占较大比重；2011年冬春季数月极端干旱持续，lag=1，2，3月时，两指标均为极端负值，保证了重旱及以上旱情有较大持续可能。

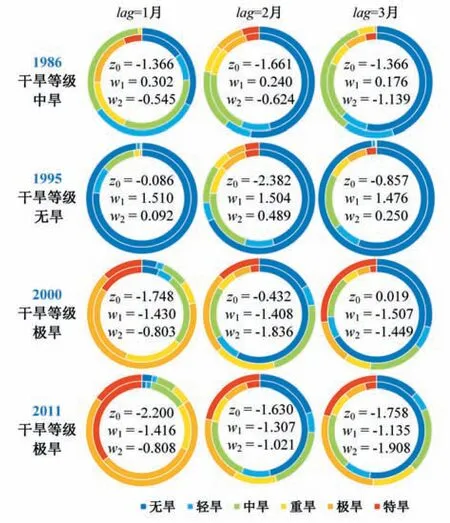
图6 定远站的历史干旱转移预测Fig.6 Prediction of historical drought transition at Dingyuan station

上述分析验证了预报模型在实际干旱事件中的应用效果，然而仍需进一步拓展待选择的气候指数的类型。Zhao et al.（2014）指出SCS，KC 和WPWP 这些局部性的气候指数与中国季节性降雨的变化有较强关联，将其作为预报因子的效果甚至比ENSO 类指数更好。降水与干旱关联紧密，故这些指数同样可以用于干旱预报，这是本文下一步的研究方向。

3 结 论

本文考虑5 种常见的大尺度气候因子，将其作为外生变量应用于淮河流域的干旱转移预测，通过R-vine Copula 构建多维变量的关联结构，并选择流域内的2个典型站点进行分析，通过结果分析得出当气候指数取不同值时，转移概率的变化情况与相关分析的结果相一致，验证了R-vine Copula 和基于PIT 的条件概率在评价气候指数对转移概率影响上的有效性，同时多维指数较单维指数更能提升预报效果，这与区域的气象干旱状态受多种大尺度气候因子调节的事实相一致。接着选取1977-2017年实际发生的干旱事件，检验纳入不同气候指数的基于R-vine Copula 的预报模型效果。当严重干旱在未来暴发或持续时，或者当严重干旱发生衰减和消退时，当前月份的气候指数均可提供关于干旱变化的有效信息，提升了干旱转移的预测精度。故本文提出的干旱预报方法可为决策者提供信息以及时调整农业灌溉、水库供水和应急调水等抗旱措施。 □