基于关联监测点数据的非线性变形预测模型

2021-04-28李柏佚王桂林

振动与冲击 2021年8期

李柏佚, 王桂林, 2, 袁军

(1. 重庆大学土木工程学院, 重庆 400045；2. 库区环境地质灾害防治国家地方联合工程研究中心,重庆 400045；3.重庆市地质矿产勘查开发集团有限公司，重庆 401121)

深基坑施工阶段伴随着变形，及时掌握其变形情况对保障深基坑的安全有着重要的意义。为此，学者们提出了很多方法对深基坑变形进行预测。目前，常用的预测方法有回归分析、灰色理论、时间序列和人工神经网络等。但是由于基坑变形序列具有较强的非平稳性及复杂的非线性特征，难以建立有效的影响因子与变形量之间的复杂关系模型。针对上述问题，有学者就采用经验模态分解(empirical mode decomposition, EMD)先将非平稳的信号转化为平稳信号，再建立预测模型来提高预测精度。罗飞雪等[1]证明 EMD 能够将边坡变形位移序列分解成具有不同尺度特征的平稳信号。吴杰等[2]将EMD算法用于大桥动态监测去噪，面对隧道爆破振动信号，邵东辉[3]采用互补集合经验模态分解法去噪，结果都证明了EMD模型具有较好的非线性映射能力、学习能力和自适应能力，能有效地提高变形预测精度，其预测精度明显优于BP神经网络(back propagation neural network)模型，较粒子群优化算法PSO(particle swarm optimization)-BP神经网络模型也有所提高。

然而，大多数的变形分析过程考虑的是变形点时间特性及观测数据序列本身的关联性，分析过程相互独立，对关联监测点之间的相互作用研究较少。但是，变形观测所获取的数据是由多个观测点在多个周期内的数据集，且监测点间彼此关联、相互影响。谢世成等[4]利用滑坡工程整体监测点变形数据建立了空间多点预测模型。对于规模较大的基坑，由于开挖施工步骤的不同，并且存在监测点空间距离间隔远，基坑各侧边坡的监测数据关联性并不大，利用整体监测点数据建立模型，可能因非关联数据导致降低预测精度。周昀琦等[5]在基坑监测中建立了临近点的变形相关性预测模型，充分挖掘变形数据中隐含的内部规律。本文以重庆某深基坑为例，对单点、多点关联、多点不关联情况下的变形预测进行对比研究，并提出基于关联监测点数据的非线性变形预测模型。

1 EMD-PSO-BPNN模型

1.1 经验模态基本原理

EMD算法根据信号的局部时变特征进行自适应的时频分解，它能将信号中不同特征尺度的数据逐步分解，并得到若干个固态函数(intrinsic mode function, IMF)分量。其中每个IMF必须同时满足两个条件[6-7]：①在整个数据段内，极值点的个数和过零点的个数必须相等或相差最多不超过一个；②在任意时刻，由局部极大值点形成的上包络线和由局部极小值点形成的下包络线的平均值为零，即上、下包络线相对于时间轴局部对称。采用EMD方法通过下面的步骤对任何信号x(t)进行分解：

步骤1确定信号所有的局部极值点,然后用三次样条线将所有的局部极大值点连接形成上包络线。

步骤2再用三次样条线将所有的局部极小值点连接形成下包络线,上下包络线应包络所有的数据点。

步骤3上、下包络线的平均值记为m1求出

x(t)-m1=h1

(1)

如果h1为一个IMF,那么h1为x(t)的第1个IMF分量。

步骤4如果h1不满足IMF的条件，将h1作为原始数据,重复步骤1～步骤3得到上、下包络线的平均值m11，再判断h11=h1-m11是否满足IMF的条件，如不满足,则重循环k次，得到h1(k)=h1(k-1)-m1k,使h1(k)满足IMF的条件。记c1=h1(k)则c1为信号x(t)第1个满足IMF 条件的分量。

步骤5将c1从x(t)中分离，得到

r1=x(t)-c1

(2)

将r1作为原始数据且重复步骤1～步骤4，得到x(t)第2个满足IMF条件的分量c2，重复循环n次，得到信号x(t)第n个满足IMF条件的分量。当rn成为一个单调函数不能再从中提取满足IMF条件的分量时，循环结束。于是得到

(3)

1.2 粒子群优化算法

PSO为一种智能优化算法[8]，能够优化BP神经网络内部结构，提高收敛速度，有效防止陷入局部极值，较快搜索全局最优解。粒子通过动态搜索跟踪个体极值和全局极值，从而实时更新粒子速度和位置，公式为

(4)

(5)

式中，w为惯性因子[9]

(6)

1.3 粒子群优化BPNN

PSO优化3层BPNN的权值和阈值。神经网络的输入层、隐含层、输出层神经元数分别设为I,H,O。记wHI为输入层与隐含层的连接权值，wHO为隐含层与输出层的连接权值，隐含层阈值θH，输出层阈值θO。粒子群中粒子的位置为BPNN中当前迭代的权值和阈值，寻找最优位置即为优化网络过程，其基本步骤如下[10-12]：

步骤1确定模型的维数D，粒子群种群规模、惯性权重和学习因子的初值，模型目标精度ε。

D=I×H+H+H×O+O

(7)

步骤2初始化粒子的位置和速度(获取随机解)，计算每个粒子的适应度值，得到个体最优Pi和全局最优Pg。

步骤3用粒子群算法式(4)、式(5)、式(6)更新粒子的速度和位置，再计算新粒子的适应度值并继续更新Pi,Pg。

步骤4以目标精度和最大迭代次数作为终止条件判断是否终止迭代。满足条件之一则完成计算，否则返回步骤3重复计算。

1.4 多监测点数据的非线性变形预测模型

基坑边坡存在竖向位移变化的多个监测点{bi|i=1，2，…，n}，将多个监测点在不同时间点的变形值作为一时间序列{xi(t)|i=1，2，…，n；t=1，2，…，m}，其中:i为监测点的序号；t为监测数据所采集的时刻，对序列xi(t)进行EMD分解得到n×q个固有模态分量IMF和n个残余分量R，其中q为单个监测点的监测数据序列进行EMD分解所得到的IMF分量个数，即

(8)

基于EMD-PSO-BPNN的关联监测点数据非线性变形预测流程，如图1所示。将q个IMF分量集合和一个残量集合分别代入PSO-BP模型中，得到各个分量集合的预测值YIMF1，YIMF2，…，YIMFq和YR，最后求各个分量预测值之和得到基坑边坡竖向位移变化的预测结果Y，即

Y=YIMF1+YIMF2+…+YIMFq+YR

(9)

图1 关联监测点数据非线性变形预测流程

1.5 模型精度评定方法

为综合评定模型的精度，采用均方根误差(root mean square error, RMSE)和平均绝对误差(mean absolute error, MAE)作为模型评价指标。平均绝对误差Em可表示为

(10)

均方根误差Erm可表示为

(11)

2 实例分析

2.1 监测数据分析

2.1.1 工程背景

重庆某深基坑所在区域位于重庆向斜西翼，场地地层主要是素填土、粉质黏土、砂质泥岩和砂岩，其中岩层倾向100°～120°，岩层倾角5°～10°，基坑最深43 m。

2.1.2 数据分析

取深基坑E面3个沉降监测点(BM09，BM10，BM11)和A面2个沉降监测点(BM16，BM17)的200期数据作为研究对象，如图2所示。由图2可知，从单个监测点看，由于周边条件复杂、扰动因素多、历时较长，监测数据都呈现变形幅度较大，呈现明显的非线性和非平稳性。但从数据整体判查，BM09，BM10，BM11的数据变化存在关联性，BM16，BM17的数据变化存在关联性。这是因为前3个测点同属E面，后2个测点同属A面监测点，显然前3个测点与后2个测点之间的数据关联性就不明显。

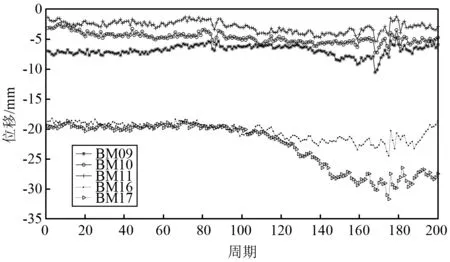
图2 A面、E面监测点原始数据变化图

从E面的3个监测点整体来看：1～80期3个监测点的数据呈现出从平稳逐步过度到轻微回弹；81～90期内呈现出一个跳跃的变化；91～160期，除了105～115期内呈现出一个跳跃的变化，监测点整体呈现出从平稳逐步过度到轻微沉降；161～200期，除了165～180期内有几个跳跃变化，整体呈现出回弹趋势。从A面的2个监测点整体来看：1～110期，数据处于平稳的状态，且局部无明显波动；111～150期，数据有明显下降，且伴随着明显的波动；151～200期，数据的波动较明显。显然，如果对该基坑边坡的沉降时间序列直接建立模型进行处理，很难得到令人满意的结果。因此，先对非平稳时间序列进行平稳化处理。本文采EMD分别对这5个监测点数据进行预处理，分解结果如图3～图7所示。由图3～图7可知，EMD可以降低边坡变形序列的非平稳性，各分量变化曲线比原曲线更光滑和平稳，有利于变形分析与预测。

图3 BM09的EMD分解结果

图4 BM10的EMD分解结果

图5 BM11的EMD分解结果

图6 BM16的EMD分解结果

图7 BM17的EMD分解结果

2.1.3 测试样本数据选择

关于BP算法中训练样本与测试样本的数据量并没一个固定的比值。如刘吉超等[13]在使用BPNN对车速进行预测时，测试样本占总体数据的比例为30%。郭彩杏等[14]在BP算法优化研究过程中，采用的比例为10%。本文选取10%作为测试样本。

基坑监测点的数据具有随机性，可以针对10%的测试样本代入式(12)[15]。

(12)

式中，当时滞k=10时，rk取得最大值0.29，故选取后10期的监测数据作为测试样本。

2.2 基于单个监测点数据的不同模型预测结果分析

以BM10为例，分别使用PSO-BPNN模型对分解得到的各分量进行训练和预测。为验证本文算法的可行性和有效性，建立3种方案进行对比分析：①BPNN模型；②PSO-BPNN模型；③EMD-PSO-BPNN模型。为了减少建模误差，所有样本数据都归一化到[-1，1]，经模型预测后再还原到原始区间。3种模型仿真结果如图8所示。3种方法的仿真效果较真实数据而言都没有出现较频繁的波动情况。通过整理得到单个监测点191～200期的3种模型的预测数据，如表1所示。由表1可知，较BPNN模型和PSO-BPNN模型，EMD-PSO-BPNN的个别预测值偏差大，但从预测总体上看，最大偏差出现在第200期，为0.709 3 mm，最小偏差出现在第197期，为0.012 3 mm；PSO-BPNN精度次之，最大偏差出现在第200期，为0.899 4 mm，最小偏差出现在第191期，为0.090 6 mm; BPNN模型精度最差，最大偏差出现在第200期，为1.230 1 mm，最小偏差出现在第191期，为0.096 2 mm。随着期数的增加，BPNN模型预测误差波动相对较大，PSO-BPNN次之，EMD-PSO-BPNN模型误差波动较小，且依然能保持良好的预测精度。

图8 基于单个监测点1～200期数据的不同模型预测结果

表1 基于单个监测点数据的不同模型的预测结果比较

2.3 基于关联监测点数据的不同模型预测结果分析

相比基于单个监测点数据的预测方法而言，关联监测点预测模型加入了BM09和BM11监测点数据。同样，为验证本算法的可行性和有效性，建立上述一样的3个不同预测模型进行对比分析，关联点的3种模型预测结果如图9所示。整理后10期预测数据如表2所示，单个监测点与关联监测点预测效果对比，如表3所示。单测点预测时，EMD-PSO-BPNN模型相对PSO-BPNN模型和BPNN模型来说，数据更稳定，其中EMD-PSO-BPNN模型残差绝对值的最大值为0.709 3 mm，最小值为0.012 3 mm；PSO-BPNN模型残差绝对值的最大值为0.899 4 mm，最小值为0.090 6 mm；BPNN模型残差绝对值的最大值为1.230 1 mm，最小值为0.096 2 mm。而当采用关联点作为数据源进行预测时，相对于单个监测点预测时，除BPNN模型中残差的最小绝对值增大了0.017 6 mm外，残差的绝对值都得到了相应的减小，EMD-PSO-BPNN模型残差绝对值的最大值减小了0.056 2 mm，最小值减小了0.012 2 mm；PSO-BPNN模型残差绝对值的最大值减小了0.067 2 mm,最小值减小了0.061 7 mm；BPNN模型残差绝对值的最大值减小了0.457 1 mm。另外，采用均方根误差和平均绝对误差这2项指标分别对单个监测点和关联监测点进行评定。由表3可知，就单点或关联点而言，EMD-PSO-BPNN模型的均方根误差和平均绝对误差都比PSO-BPNN和BPNN模型的更小；就同种预测模型，关联点相对单点而言均方根误差和平均绝对误差都更小。显然，基于关联监测点的EMD-PSO-BPNN网络模型具有较高的预测精度，可信度较高。

表2 基于关联监测点数据的不同模型的预测结果比较

图9 基于关联监测点1～200期数据的不同模型预测结果

表3 单点与关联点的3种模型精度评价

2.4 基于非关联监测点数据的EMD-PSO-BPNN模型预测结果分析

表3中，呈现了单点与关联点的3种模型精度评价。不论是单点还是关联点EMD-PSO-BPNN模型都是最优的，所以本小节只采EMD-PSO-BPNN模型来对非关联监测点数据进行预测并进行预测结果精度分析。

本模型中选择了与BM10监测点不在同一个基坑侧面的监测点BM16和BM17，从监测数据来看，这两个监测点的数据明显与BM10测点不同，关联性远不如BM09和BM11监测点。后10期数据统计的残差、均方根误差、平均绝对误差如表4所示。图10为基于关联点和非关联监测点数据的预测结果。可见，基于非关联点的监测数据对变形预测有干扰。图11为BM10监测点19～200期数据的不同模型预测结果。