基于虚拟介质方法数值模拟应力波穿透水舱

史汝超， 孙晓旺

(1.江苏海洋大学 理学院，江苏 连云港 222005；2.连云港中复连众复合材料集团有限公司，江苏 连云港 222023； 3. 南京理工大学 机械工程学院，南京 210094)

水舱是舰艇的常见装置，可分为压载水舱、补重水舱、间歇水舱等多种专用水舱。应力波穿透水舱是一个典型的流固耦合问题，常见于舰艇的防护设计和抗爆抗冲击研究[1-3]。目前，数值模拟该类问题较常使用的方法是SPH(smoothed particle hydrodynamics)[4]和ALE(arbitrary-Lagrangian-Eulerian)方法[5]。这两种方法适用性很广，因此，大部分主流商业软件，如ANSYS、Abaqus等，都是基于这两种方法开发的。然而，如果想非常精确地求解并刻画固体中的应力波，很多时候需要使用数值精度较高的有限差分法，选择特定的差分格式，并设以特定的时间步长和空间网格。目前，完全使用有限差分法处理流固耦合问题的计算方法是虚拟介质方法[6-7]。

虚拟介质方法可进一步细分为OGFM法则(original ghost fluid method)[8]、MGFM法则(modified ghost fluid method)[9]和RGFM法则(real ghost fluid method)[10]。收敛性较好的是MGFM法则和RGFM法则，均已初步推广至水下冲击波冲击流固界面问题，可获得很好的模拟效果[11-13]。本文进一步以MGFM法则为基础，将虚拟介质方法推广至固体应力波在流固界面处的折射问题，并以此为基础，数值模拟应力波穿透水舱。

1 虚拟介质方法

1.1 流体控制方程

二维轴对称欧拉方程可写为

(1)

其中，

(2)

(3)

(4)

(5)

式中:ρ为密度；p为压力；u，v，w为x，y，z方向的速度;r为任一点至y轴的距离；单位质量总能E=ρ(u2+v2+w2)/2+ρe。对于一维问题，式(1)可简化为

(6)

1.2 固体控制方程

取压应力为负值、拉应力为正值。固体的二维轴对称弹性动力学方程可写为

(7)

其中，

(8)

(9)

(10)

(11)

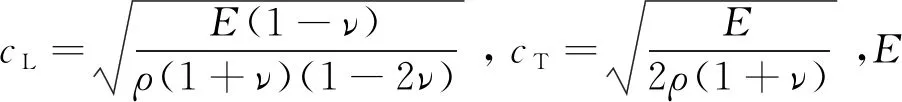
(12)

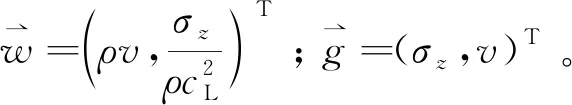
1.3 近似黎曼解算器

流固界面在数学上属于黎曼问题。图1 给出了求解黎曼问题的特征线法示意图。在流固界面处沿特征线差分，可得到界面处的差分近似解。图中固体设定在界面左侧，故取右特征线方程

dσ-ρcdu=0

(13)

式中，c为声速。流体在界面右侧，故取左特征线方程

dp-ρcdu=0

(14)

式(11)、式(12)分别向后和向前差分

(15)

式中：下标“I”为界面处的参数；上标“n”，“n+1”为时间步。

在流固界面处：当固体处于受压状态，界面受力方向从流体指向固体，pI=-σI；当固体处于受拉状态，界面受力方向从固体指向流体，pI=σI。

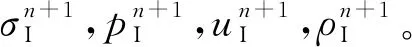
水的密度可由等熵状态方程确定

(16)

式中：N为水的绝热指数；ρ0=1.0×103kg/m3；A=1.0×103Pa；B=3.31×108Pa。

在流固界面变形较小的情况下，求解固体一侧的网格坐标

(17)

图1 特征线法求解黎曼问题

1.4 MGFM赋值法则

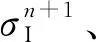
(18)

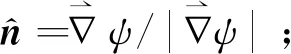
(19)

式中，dis为点与面之间的最短距离。

图2 MGFM赋值法则

在数值模拟中，由于界面的移动，流体虚拟节点有时候会转变为真实节点。根据等熵修正思想，为避免数值振荡，用相邻真实节点的状态代替虚拟节点的状态(见图3)。

图3 赋值修正步

1.5 数值模拟步骤

选取无量纲参考态：压力pref=0.1 MPa,密度ρref=1.0×103kg / m3，长度lref=1.0 m，速度uref=10 m/s，时间tref=0.1 s。用Zwas格式[15]离散固体控制方程；用五阶WENO格式[16]离散流体控制方程；用三阶Runge-Kutta方法离散时间项。使用欧拉网格离散流体区域，并求解网格节点的状态值；使用欧拉网格求解固体区域并求解网格中心的值。数值模拟步骤如下：

步骤1用近似黎曼解算器成对求解界面两侧的流体网格节点和固体网格中心的状态；

步骤2用1.4节中的赋值法则对虚拟区域赋值；

步骤3用当前时刻的状态值求解下一时刻流体网格节点(包括虚拟节点)和固体网格中心(包括虚拟网格中心)的值；

步骤4用式(17)求解界面位置，并根据新界面重新划分真实区域和虚拟区域；

步骤5回到步骤1进行一下时间步的求解。

2 数值测试

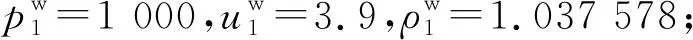
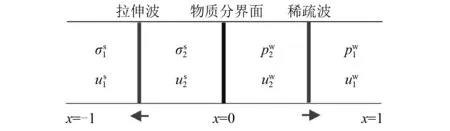
图4 固体侧的拉伸波与流体侧的稀疏波示意图

将计算域划分为400个网格，网格步长Δx=0.005。水的绝热指数N=7.15；固体密度ρ=7.8、弹性模量E=2.06×106、泊松比ν=0.25。图5表明数值结果和理论结果吻合很好且没有数值振荡。其中，理论结果的求解可参考文献[17]。稀疏波的理论解在左右两端各有一个折点；而稀疏波的数值解，由于数值误差，两端折点不明显。表1给出了固体区域和流体区域的数值误差，本文给出的赋值法则具有一阶收敛精度。

图5 拉伸波与稀疏波的数值结果(t=1.243 429×10-3)

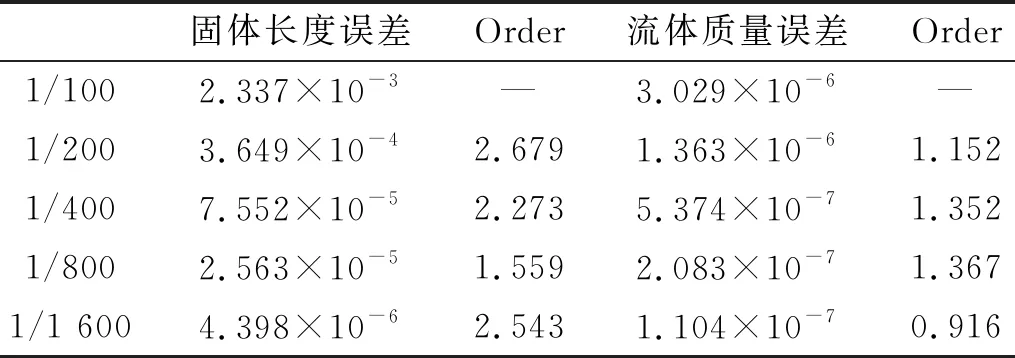
表1 数值测试结果

3 一维数值模拟

水舱壳体中的应力波一般由水或者空气中的压缩波透射产生,如图6所示。压缩波透射产生固体应力波后，才能进一步在舱内产生另一道透射压缩波。本节分别对水和空气中的压缩波穿透问题数值验证。以下计算中，取网格步长Δx=0.005；空气绝热指数γ=1.38；水的绝热指数N=7.15；固体密度ρ=7.8、弹性模量E=2.06×106、泊松比ν=0.25。

3.1 空气中的压缩波穿透水舱

图6 空气/水中的压缩波穿透水舱

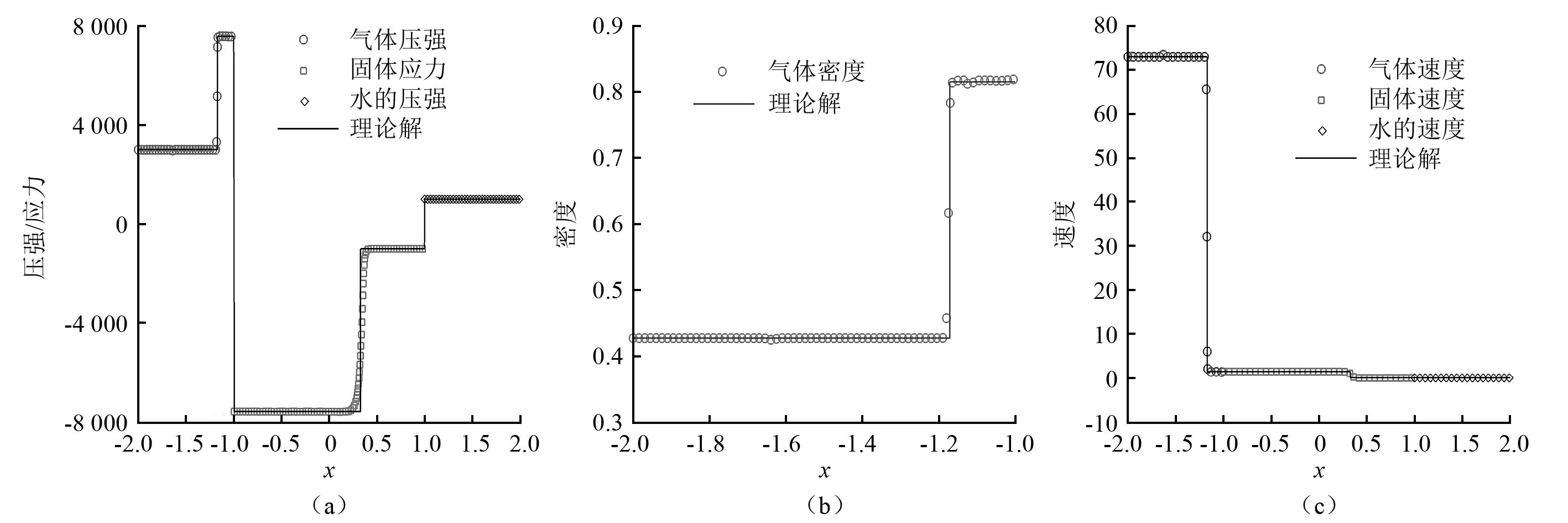
图7 空气中的压缩波进入水舱壳体生成固体应力波(t=5.892 452×10-3)

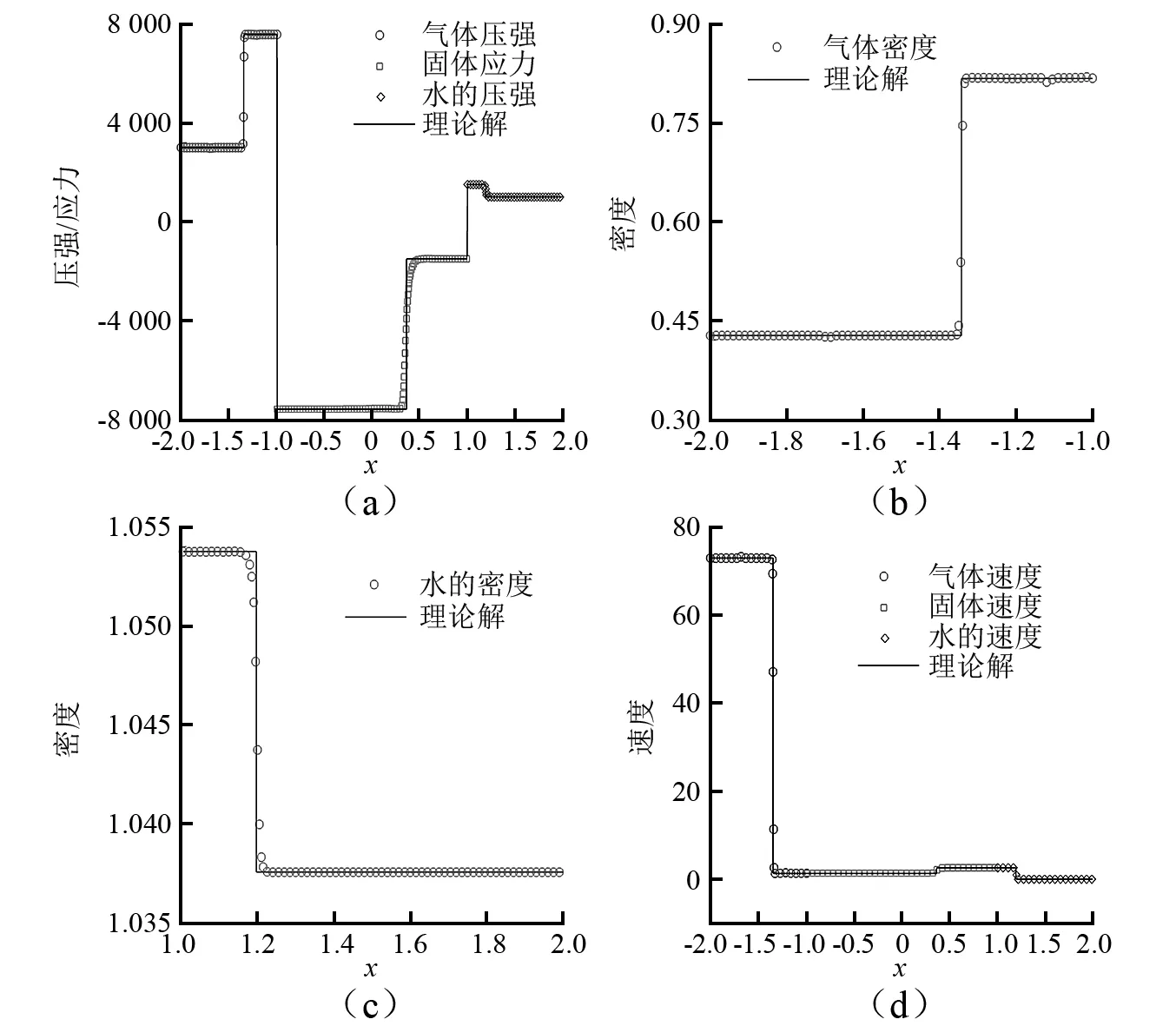
图8 固体应力波进入水舱生成水中压缩波(3.1节)(t=8.081 076×10-3)

3.2 水中压缩波穿透水舱

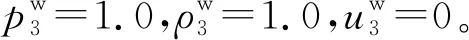
3.1节与3.2节中的数值结果均与理论解吻合一致。虽然虚拟介质方法中的流固界面在数值模拟时是连续的，但是在数学上仍然是间断的。这使得在数值模拟时，流体与固体必须分开求解，从而导致数值结果与理论解在局部区域有一些较小的差异。但是，这些误差是收敛的，并没有随着计算的进行而逐渐增长。

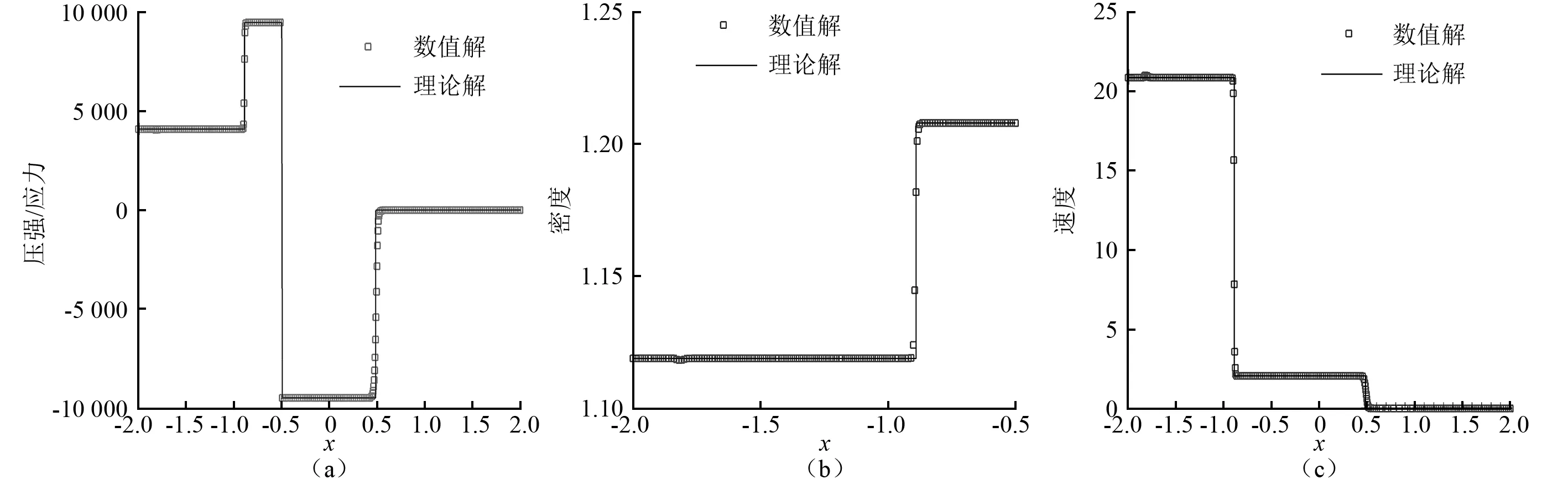
图9 水中的压缩波进入水舱壳体生成固体应力波(t=4.208 894×10-3)

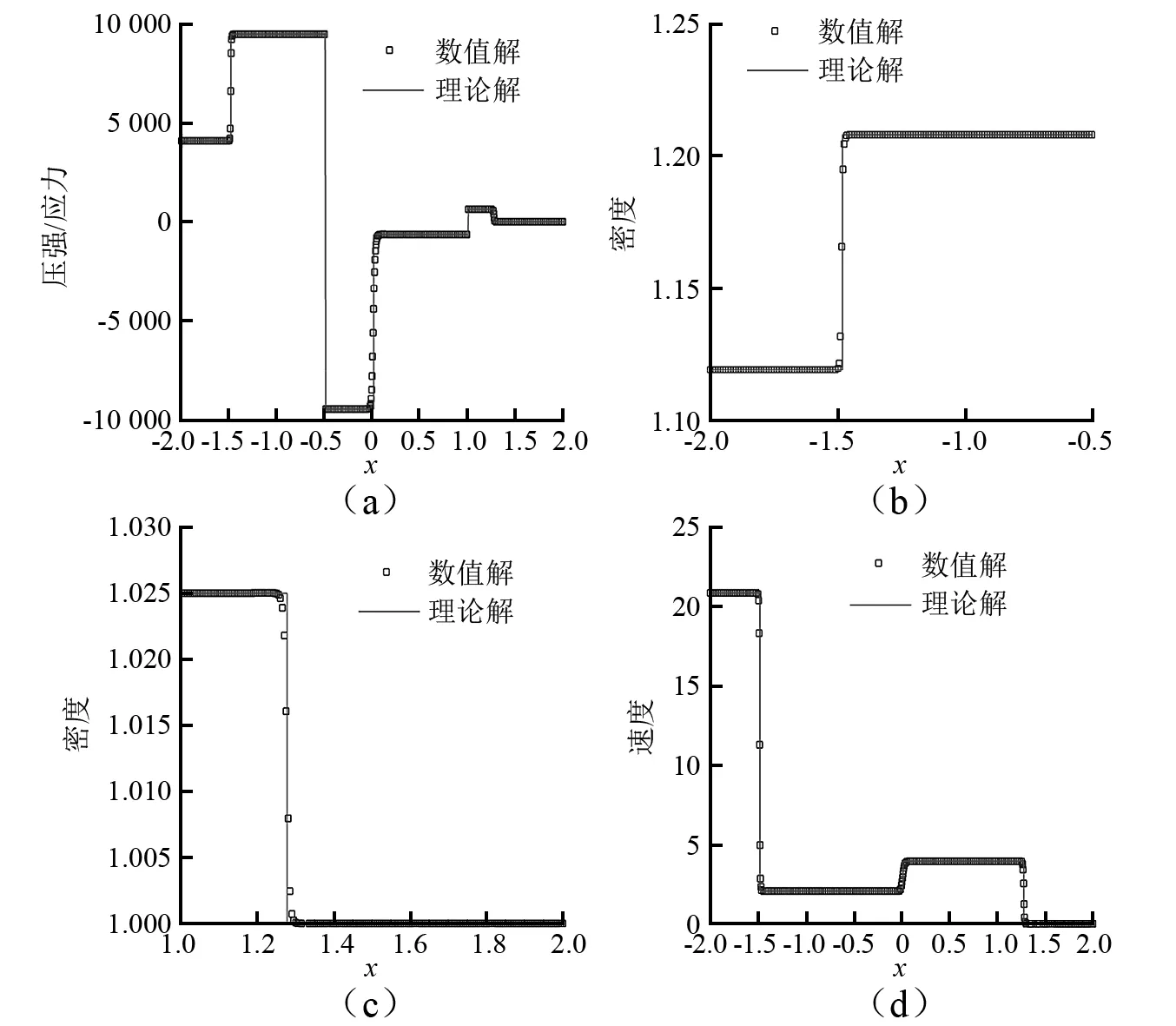
图10 固体应力波进入水舱生成水中压缩波(3.2节)(t=6.734 230×10-3)

4 二维轴对称数值模拟

图11给出了一个水舱中心计算域的示意图。计算域底面半径0.5，高度1.0，壳板背面压力分别取pw=100 kPa,200 kPa,400 kPa,800 kPa，取该中心区域的中轴面(虚线区域)建立二维轴对称坐标系，网格步长为Δx=Δy=0.005。水的绝热指数N=7.15。壳板无量纲参数为：密度ρ=7.85、弹性模量E=2.06×106、泊松比ν=0.28、屈服强度4 000、抗拉强度4 800。

在底面中心A点按图12加载应力，加载范围为直径0.01的圆形区域。图13(a)描绘了应力波在水舱壳体内部的传播。如图13(b)所示，在t=1.122×10-3时，应力波波阵面已经到达水舱壳体背面。图14(a)、图14(b)分别给出了由虚拟介质方法和ALE方法得到的背面中心B点的动态响应。由于数值耗散，背面中心B点的应力大约在t=7.0×10-4时开始增加。但波阵面大约于t=1.0×10-3时，到达背面中心，此时，应力显著增加。ALE算法在流固界面处采用弱耦合形式，只使用迎风面(壳体侧)的状态参数，界面应力在峰值之前上升略早，峰值时间略晚；虚拟介质方法在流固界面处采用强耦合形式，即同时使用界面两侧的状态参数，界面应力在峰值之前上升略晚，峰值时间略早。两种方法得到的数值结果差异较小，应力变化趋势相近。表2表明，当水舱内的环境压力增加后，应力峰值也相应的增加，峰值时间近似保持不变；同时也验证了虚拟介质方法与ALE方法所得到的应力峰值和峰值时间相近。图15表明水舱压力越大，透射波强度越大；同时，由于4个算例(pw=100 kPa,200 kPa,400 kPa,800 kPa)均使用相同的应力加载，壳体背面的应力波折射规律相近。

图11 水舱中心计算域示意图

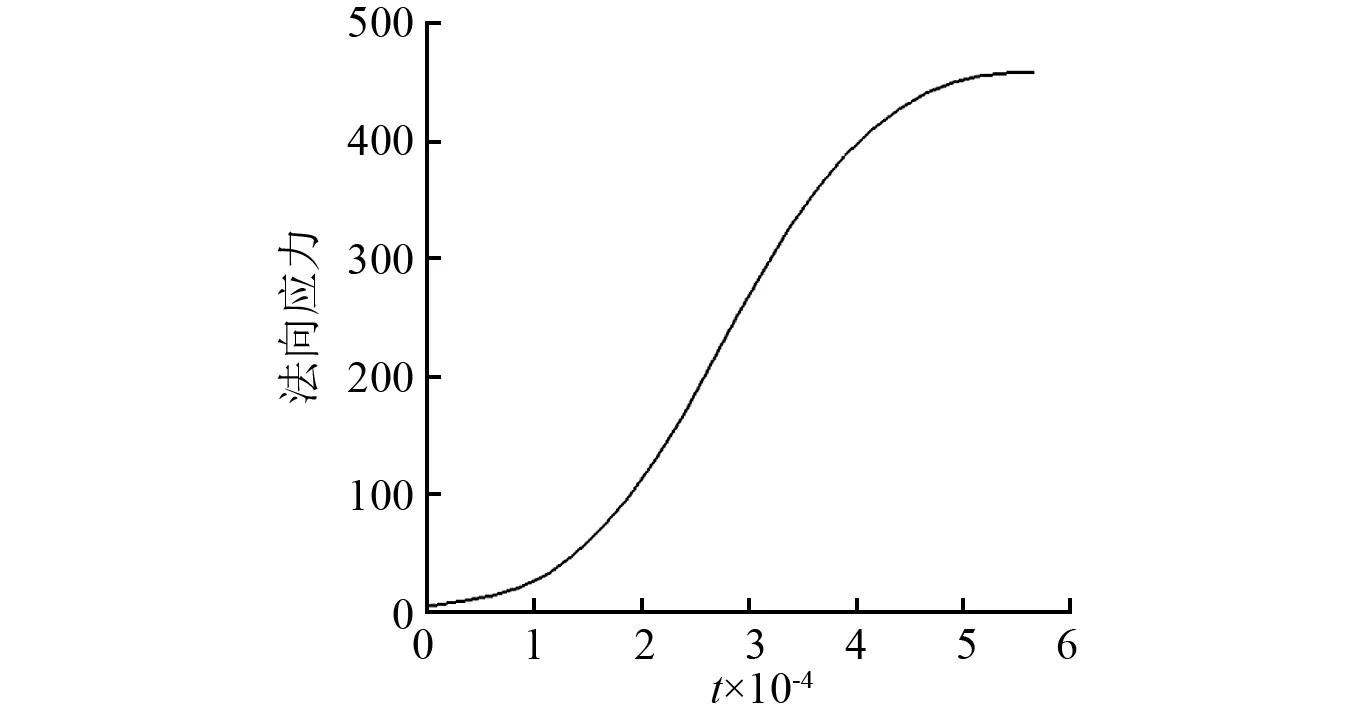
图12 应力加载曲线

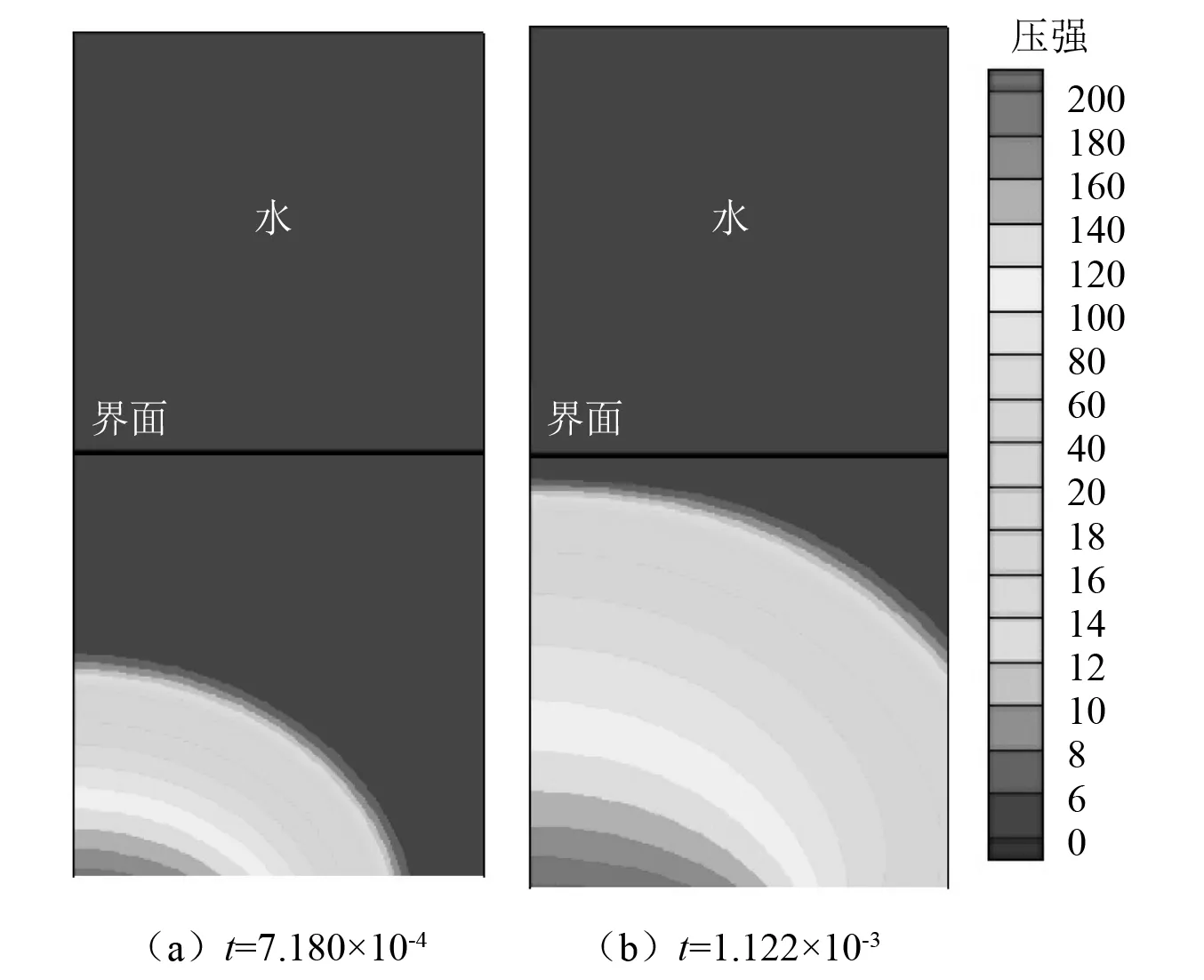
图13 固体中的应力波传播(固体压强ps=∑|σi|/3)

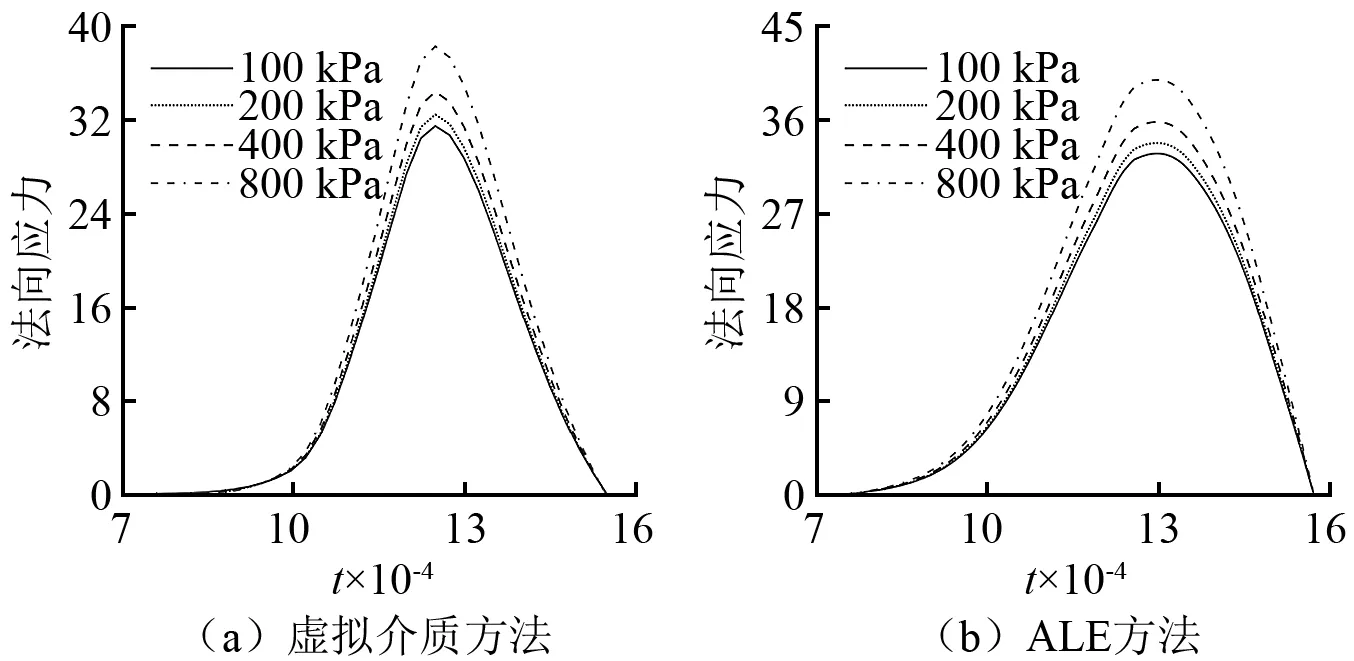
图14 水舱壳体背面动态响应

表2 峰值数值结果

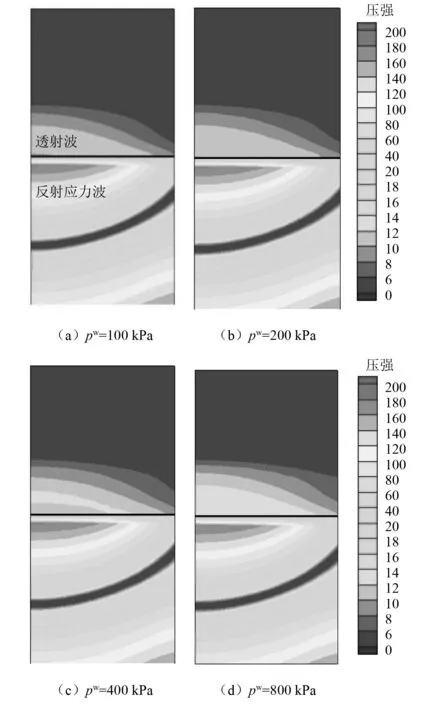
图15 应力波在壳板背面的折射 (t=2.486×10-3，固体压强ps=∑|σi|/3)

5 结 论

本文将虚拟介质方法应用到应力波在流固界面处的折射问题，并给出了对应的计算法则；数值测试表明，提出的计算法则具有一阶精度。本文对水舱壳体中的应力波穿透水舱的过程进行了数值模拟和理论分析，一维数值结果与理论解能很好地吻合。多维数值模拟验证了虚拟介质方法与ALE方法得到数值结果相近。对应力波穿透水舱的初步研究表明，水舱加压后，透射波的强度也相应地增加；在不改变初始应力加载的情况下，应力波在水舱壳体背面的折射规律也对应的近似不变。