基于多体动力学与离散元耦合的惯性圆锥破碎机动态性能研究

程加远， 任廷志， 张子龙， 刘大伟， 金 昕

(燕山大学 国家冷轧板带装备及工艺工程技术研究中心，河北 秦皇岛 066004)

目前，在颗粒状矿物料加工破碎过程中，圆锥破碎机起着至关重要的作用，广泛应用于矿物加工粉碎作业的第二、第三级破碎阶段[1]。在矿石性质复杂的选矿过程中，惯性圆锥破碎机作为一种很有发展前途的圆锥破碎机是不可缺少的破碎设备之一[2]。惯性圆锥破碎机的挤压破碎作用通常是在一定章动角范围内，使动锥相对于定锥产生旋摆运动来实现的。该旋摆运动是由偏心激振器通过连接轴将驱动轴的旋转运动传递到主轴，且由于物料作用使动锥发生纯滚动。但是，由于其独特的原理和工作环境，其作业时会受到各种载荷的激励，例如：偏心激振器的不平衡惯性力造成整机振幅大且能耗高；进料性质的不均匀导致产品指标下降等，这些因素直接决定了其动态响应和工作参数不同于其它类型圆锥破碎机，例如液压圆锥破碎机和西蒙斯圆锥破碎机。因此，能否改善惯性圆锥破碎机动态特性和优化工作参数已成为现代破碎行业需解决和突破的关键技术之一。

目前，针对惯性圆锥破碎机动态性能的研究，国内外学者主要以空载或者忽略物料作用开展整机系统的仿真和试验等相关研究[3-5]。王晓波等[6]利用内行星-振动机体系统模型进行研究，结果表明当惯性圆锥破碎机稳定工作时，动锥自转的角速度与其半径以及排料间隙有关。卫一川[7]采用ANSYS软件提取了关键部件的前十阶固有频率及振型，并与其固有频率进行对比。Mitrev等[8]采用理论与实验结合方法对橡胶减振器的刚度和阻尼参数进行估计校准。Kazakov等[9]基于三质量系统模型对振动圆锥破碎机进行动力学建模，但忽略颗粒与设备之间的接触作用。在考虑物料颗粒与设备相互作用研究中，赵月静等[10]将物料层的作用简化为分段线性的接触力，结果表明，物料层的作用使得系统刚度变大，固有频率增大。Evertsson等[11]利用EDEM软件中的黏合键模型(bonded particle model,BPM)对液压圆锥破碎机进行了建模，研究了闭边尺寸对产品粒度分布、液压力和功率消耗的影响。Li等[12]和Cleary等[13]利用球和非球形颗粒的粒子群平衡替换模型(population balance replacement model,PBRM)研究了进料性质和操作条件对产品性能的影响。以上基于离散元法的仿真模型由于忽略了颗粒对破碎机运行的影响，因此这些模拟无法预测设备的动力学特性随颗粒载荷变化的规律。

采用多体动力学(multi-body dynamics,MBD)[14]与离散单元法(discrete element method,DEM)[15]耦合对含破碎颗粒的惯性圆锥破碎机进行动力学仿真，是改善破碎机动态性能和优化工作参数的有力方法之一。目前国内外学者还没有针对惯性圆锥破碎机进行MBD和DEM耦合系统仿真的相关研究。本文在详细推导惯性圆锥破碎机动力学方程的基础上，建立了基于黏合键破碎颗粒和多体系统的双向耦合仿真模型，并通过工业现场试验验证了耦合仿真模型的有效性。采用该模型，分析了物料流动特性和腔内破碎力分布规律，进一步研究了不同转速和定锥质量等关键参数对动态性能和产品指标的影响，并给出了几点重要结论。本文建立的惯性圆锥破碎机MBD-DEM耦合仿真模型对破碎机破碎特性的研究具有一定参考价值，且为优化惯性圆锥破碎机结构和工作参数提供了一种验证方法。

1 惯性圆锥破碎机MBD-DEM耦合动力学模型

本文所针对惯性圆锥破碎机源自唐山某钢铁企业，GYP 1200型破碎机如图1所示，其主要由凹锥、凸锥、球面轴承、偏心激振器、驱动轴和主架等构成。

图1 GYP 1200型惯性圆锥破碎机组成

1.1 考虑颗粒的绝对坐标法建模

通过惯性圆锥破碎机各个运动副来约束相对运动，并采用绝对笛卡尔坐标法推导了多体系统的动力学方程[16]。为了简化MBD模型，本文采用的理想化假设如下：①惯性圆锥破碎机的所有部件都假定为刚体；②输入转速稳定且不变化；③橡胶减振器的刚度和阻尼值是恒定；④运动副摩擦因数的值是恒定；⑤进料颗粒具有相同材料特性和均匀尺寸；⑥颗粒均匀分布在破碎室中，且破碎室充满破碎颗粒。基于以上假设，图2表示带黏结颗粒的惯性圆锥破碎机的简化动力学模型。图2中：l0为惯性圆锥破碎机中心轴线；l1为定锥中心轴线；l2为动锥中心轴线；θ为定锥与动锥之间章动角；α为凸锥结构底角。凹锥被固定在主机架上，称为定锥(B1)。凸锥被固定在主轴上，称为动锥(B2)。定锥与动锥约束副为球铰(O1)；球面轴承(B4)与定锥约束副为球铰(O2)；偏心激振器(B3)与动锥为圆柱副(O3)；偏心激振器与球面轴承为平面副(O4)；偏心激振器与连接轴(B5)为球销副(O5)；连接轴与驱动轴(B6)为十字方向副(O6)；驱动轴与地面(B0)为旋转副(O7)。橡胶减振器与定锥之间的作用力相当于衬套力，其中考虑了刚度系数(kx,ky和kz)和阻尼系数(cx,cy和cz)。

该动力学模型使用七个坐标系：一个全局坐标系(cxyz)0,六个局部坐标系(cxyz)i(i=1,2,3,4,5,6),其原点分别为各刚体Bi(i=1,2,3,4,5,6)的质心。在没有任何约束的全局参考系中的刚体(Bi)有三个独立的位置变量(xi,yi,zi,)和三个独立的欧拉角变量(ψi,θi,φi)，它们被定义为Bi的广义坐标。Bi广义坐标的列矩阵qi可以表示为

(1)

式中： 上标T为数组转置的常用符号；ri为广义位置坐标的列矩阵；Λi为广义欧拉角坐标的列矩阵。惯性圆锥破碎机广义坐标q可以表示为

(2)

图2 带黏结颗粒的惯性圆锥破碎机简化动力学模型

用牛顿-欧拉公式[17]导出了各刚体(Bi)广义坐标动力学方程，可表示为

(3)

(4)

Qi=

(5)

式中： 上标～为列矩阵的反对称矩阵； 上标(i)为矢量或矢量矩阵在局部坐标系(cxyz)i中的坐标；mi为Bi的质量；Ji为Bi相对质心的惯性矩阵；E为单位阵；0为零阵；Fia和Tia分别为等效阻尼力和力矩；Fif和Tif分别为运动副等效摩擦力和力矩；Fig为重力；Fic和Tic分别为等效接触力和力矩；Fip和Tip分别为颗粒的等效作用力和力矩。矩阵Di可表示为

(6)

无约束方程惯性圆锥破碎机的动力学方程可表示为

(7)

由多体系统的运动副Oj(j=1,2,3,4,5,6,7)引起的完整约束和驱动轴的驱动约束可用完整约束方程进行描述，表示为

Φ(q,t)=0

(8)

式中，Φ(q,t)=[Φ1(q,t),Φ2(q,t),… ,Φ25(q,t)]T假设是独立的,式(8)的雅可比矩阵被定为

(9)

式(8)给出了速度和加速度关系可表示为

(10)

其中，矩阵ζ表示为

(11)

利用拉格朗日运动方程的拉格朗日乘子公式，导出了惯性圆锥破碎机的动力学方程，可表示为

(12)

式中，λ为拉格朗日乘子的列矩阵，进一步表示为

λ=(λ1,λ2, … ,λ26)T

(13)

1.2 凸锥与凹锥非线性接触模型

如果凸锥和凹锥相互靠近，它们最终会接触或碰撞，并在它们之间产生相互作用力，惯性圆锥破碎机有这种接触问题，而液压和西蒙斯型圆锥破碎机不存在此接触。凸锥和凹锥之间的碰撞实例如图3所示，接触力Fic[18]计算为

Fic=fn+ft

(14)

式中：fn和ft分别为法向约束力和摩擦力，如果重叠量记为δ，则法向力变为

(15)

式中：k和c为弹性和阻尼系数；h1和h2为弹性和阻尼的指数；h3为缩进指数。

弹性系数k随两个物体的材料和形状以及接触点的相对速度而变化。Hertz从理论上推导出弹性系数k在两个球体之间变化，可以表示为

(16)

式中，ri,Ei和νi分别为第i个球体的半径、杨氏模量和泊松比。

图3 凸锥与凹锥碰撞接触

设t为与两物体间滑动面相切的单位矢量，v1和v2为定锥(B1)和动锥(B2)上接触点处的绝对速度矢量。然后，摩擦力为

|ft|=μ(v)|fn|

(17)

式中，μ(v)为带符号的摩擦因数。如果v是B2相对于B1沿t的相对速度，则v可以表示为

v=(v2-v1)·t

(18)

式中，v1,v2和t以矢量形式表示，相对于全局坐标系(cxyz)0。

在这种情况下，使用参数值给出摩擦因数，这种情况只考虑滑动运动。摩擦因数μ(v)由式(19)定义[19]

μ(v)=

(19)

式中：μd和μs分别为动摩擦和静摩擦阈值系数；vd,vs和v分别为动态阈值速度、静态阈值速度和切向相对速度。函数hav sin(x,x0,h0,x1,h1)可表示为

(20)

本文对工业级GYP 1200型惯性圆锥破碎机进行建模，用RecurDyn软件对无颗粒惯性圆锥破碎机的MBD进行了仿真。在表1中，给出了MBD仿真参数。

表1 MBD仿真参数

1.3 基于DEM的颗粒压碎模型

DEM采用逐步算法对每个粒子的运动方程进行数值积分，对于惯性圆锥破碎机的DEM仿真，使用了两种不同的模型:在颗粒之间或颗粒与几何体之间采用Hertz-Mindlin接触模型[20]，如图4所示；黏结粒子模型[21]，如图5所示。Hertz-Mindlin接触模型将接触力Fp分解为法向分量Fpn和切向分量Fpt，其法向分量Fpn可表示为

Fpn=Fpn,s+Fpn,d

(21)

式中：Fpn,s为法向弹簧力；Fpn,d为法向阻尼力，表示为

(22)

(23)

(24)

图4 Hertz-Mindlin接触力模拟粒子间或与几何体间的碰撞

接触力的切向分量Fpt，可表示为

Fpt=Fpt,s+Fpt,d

(25)

式中：Fpt,s为切向弹簧力；Fpt,d为切向阻尼力，可表示为

(26)

|Fpt|≤μ|Fpn|

(27)

式中，μ为摩擦因数。在Hertz-Mindlin接触力模型中，接触摩擦和接触阻尼是粒子系统能量耗散的两个重要机制，所需参数为泊松比v,剪切模量G,颗粒与几何体之间摩擦因数μw，颗粒之间摩擦因数μp，颗粒与几何体之间恢复系数ew，和颗粒之间恢复系数ep。

黏结粒子模型是基于将球的堆积分布结合或黏合在一起形成一个破碎体。结合在一起的粒子称为元粒子，而产生的团簇被定义为破碎颗粒。每个键接触处力-位移行为的理论梁由定义的平行键以下五个参数描述：单位面积法向kbn和剪切刚度kbt; 拉伸σbc和剪切强度τbc；键半径乘子λb；平行键半径Rb表示为

Rb=λbmin(r(i),r(j))

(28)

式中，r(i)和r(j)分别为粒子i和粒子j的半径，平行键可以在粒子之间传递力和力矩，而粒子只能传递力，这些弹簧就像一根梁，其长度Lb接近于零。

图5 颗粒黏结键的力-位移

Fb和Tb分别为平行键承受的总力和力矩，表示为

Fb=Fbn+Fbt,Tb=Tbn+Tbt

(29)

式中，Fbn,Fbt和Tbn,Tbt分别为法向力，切向力和法向力矩，切向力矩。根据Hertz-Mindlin接触模型，在键形成之前和键断裂之后，粒子相互作用，Fb和Tb设为零。键形成后，每个随后的相对位移和旋转增量(ΔUn,ΔUt,ΔΘn,ΔΘt)产生的弹性力和力矩增量被加到当前值中。当颗粒黏合时，力和扭矩根据式(30)进行调整。

(30)

式中，A和J分别为平行键截面的面积和极惯性矩。这些量可表示为

(31)

根据式(32)的梁理论，计算作用在平行黏结周边的最大法向和切向应力

(32)

如果最大拉伸应力超过拉伸强度或最大剪切应力超过剪切强度，如式(33)所示，则平行键断裂。

(33)

1.4 BPM参数标定

当使用DEM对破碎进行建模时，关键在于确保控制破碎的BPM符合实际破碎行为。如果BPM参数不正确，破碎颗粒将以不正确方式破碎，则BPM参数校准是非常重要。首先，进行了一系列巴西劈裂抗拉实验和单颗粒压碎实验，以记录破坏的临界力和压缩比，估算岩石材料的强度。其次，利用正交实验方法对岩石破碎过程进行仿真。最后，将实验数据与仿真结果的误差降到最小，并以最佳参数作为BPM模型的校准参数。

1.4.1 双峰分布粒子堆积团簇

通过使用粒径相对较大的双峰分布和较小的双峰分布的颗粒产生黏结作用，为用最少的颗粒数来实现高堆积密度和良好的破碎特性提供了最佳的可能性[22]。在本研究中，岩石材料为白色大理岩，因此双峰分布的大径部分(正态分布)设置为平均球体半径为3 mm，标准偏差为0.525 mm，而双峰分布的较小部分(正态分布)设置为平均尺寸为1.05 mm，标准偏差为0.225 mm，计算出颗粒床的堆积密度为0.82。岩石的三维扫描模型用作破碎颗粒团模型，可用于破碎机工作仿真，如图6所示，采用了四种不同的破碎颗粒大小和形状与试验中的进料分布相对应。

图6 三维扫描岩石模型生成具有真实形状的破碎颗粒

1.4.2 颗粒破碎实验

对白色大理岩样品进行了巴西实验[23]，这些样品的差异导致了破坏圆柱形岩石样品所需的临界力和压缩比不同，如图7所示。6次巴西试验的力-位移曲线如图8所示。从曲线中可以看出，力累积到样品破裂，破裂时的峰值力被定义为临界力，此时压缩比被定义为临界压缩比

根据数据计算出临界力的平均值为14.8 kN，由式(34)得到平均强度为3.77 MPa。

σt=2Fc/πDL

(34)

式中：Fc为临界力；D为样品直径；L为样品厚度。

1.4.3 田口正交法的破碎仿真

在巴西试验中，破碎颗粒的反应机理通常是复杂的、高度非线性的，因此，选择临界力和临界压缩比作为响应的评估指标。圆柱状岩石仿真试验与巴西劈裂试验相似，如图9所示，断裂颗粒的键结构和力网络清晰可见，断裂的键呈黑色。BPM参数的校准是基于16种不同因素组合仿真，采用是Hanley等[24]使用的正交法仿真实验设计。

图7 白色大理石颗粒破碎

图8 6次巴西劈裂实验的力-位移曲线

图9 圆柱形破碎颗粒的巴西劈裂模拟

表2列出巴西实验模拟所用的参数(因子)及其设置(水平)。选择了L16(45)阵列，因为它可以在四个水平上容纳多达五个因子(包括误差因子)，根据Wang等[25]给出的结果，刚度比kbn/kb被设置为2.5。

表2 巴西试验模拟采用5因数4水平的标准L16数组

1.4 4BPM校准参数

数据使用Minitab 16进行分析，首先，将方差分析应用于每个响应模拟所获得的原始数据，如表3所示。力差Fcd定义为

Fcd=|Fcs-Fcav|

(35)

式中：Fcs为来自模拟的临界力；Fcav为来自实验的平均临界力。

在方差分析中，选择力差Fcd和临界压缩比作为评价响应，用F值评估统计显著性：如果F值大于临界F值，则在90%显著性水平下，效应被认为是显著的。为了有助于结果的可视化，统计上显著的效果用粗体和斜体表示，显然，影响力差的主要参数是剪切临界应力和剪切刚度。对于临界压缩比，影响最大的参数是剪切临界应力和法向临界应力且黏结半径也是非常有影响的参数，在90%显著性水平下具有统计学意义。通过综合分析，得到了最佳的BPM参数：剪切临界应力9 MPa，法向临界应力25 MPa，剪切刚度160 GPa/m，黏结半径3.1 mm。在这项研究中，DEM仿真是使用EDEM软件进行的,表4给出了DEM的详细仿真参数。

表3 两种模拟响应的方差分析结果

表4 DEM仿真参数

2 耦合模型仿真方案及试验验证

2.1 MBD-DEM模型仿真

本文对惯性圆锥破碎机耦合模型仿真的流程图，如图10所示。在仿真开始时，输入机械部件和颗粒的几何和材料参数。DEM环由EDEM软件计算，确定每个粒子的位置和速度以及粒子之间和粒子与几何体之间的作用力。在DEM环结束后，DEM将几何体上的等效粒子力和力矩发送到MBD环，MBD环由RecurDyn软件实现求解MBD的控制方程，并计算几何体的位置和速度。对工业级(型号：GYP1200)带有黏结颗粒模型四种不同形状给料破碎颗粒(直径为50 mm)的惯性圆锥破碎机进行了MBD-DEM耦合仿真。

2.2 工业试验

为了验证该耦合动力学模型，在唐山某钢铁厂进行了试验。进料岩石材料是白色大理石，为了得到-50 mm的进料，每个样品首先在一个50 mm孔径的筛子上被分开。采用位移和加速度传感器(型号：DH311E，东华测试技术)，在0～1 000 Hz的测试频率范围内，测量了主机架在x，y，z方向的位移和加速度。采用动态信号采集仪(DH5902，东华测试技术)采集位移和加速度数据。在破碎流程控制系统中可直接测量破碎机功率消耗数据，并用孔径筛获得了试验产品的粒度分布，GYP 1200型破碎机试验装置，如图11所示。

图10 MBD-DEM耦合模型计算流程图

测试点的位移和加速度由位移和加速度传感器测量，如图11(b)所示。驱动轴转速设置通过破碎流程控制系统仔细校准，如图11(c)所示。为了得到产品的尺寸分布，排料产品在一系列的孔径筛上被筛分，如图11(d)所示。在400 r/min和600 r/min下对试验数据和仿真结果进行了比较。

图11 GYP 1200型破碎机试验装置

2.3 耦合模型验证

2.3.1 测试点位移

在惯性圆锥破碎机中，偏心激振器运动通过动锥传递到定锥，则定锥的位移振幅是反映惯性圆锥破碎机振动特性的重要指标之一。该测试点是位于距离橡胶减振器上端900 mm处主架观察口上，在破碎机运行1 s内，测试点x，y，z方向位移的仿真结果和测量数据，如图12所示。从图12(a)或图12(b)可以看出，仿真和测量的位移显示出频率为6.7 Hz或10 Hz的循环行为，且该频率与偏心振动器的频率一致。

图12 x，y，z方向位移的仿真与试验对比

2.3.2 功率消耗

功率消耗是一个重要的性能指标，它能显示破碎机工作过程中的能量消耗。驱动轴的输出功率用于以下几个部分：破碎机的空载机械能、破碎岩石和机械阻尼引起的能量损失。破碎流程控制系统可直接测量试验功率消耗数据，其功耗数据为驱动电机输入功率，则驱动轴输出功率为试验数据乘以电机驱动效率。

驱动轴输出功率的试验和仿真对比，如图13所示。试验和仿真结果表明，由于破碎颗粒均匀分布在破碎室中，破碎机的输出功率在小范围内呈现波动行为。在比较试验和仿真输出功率的平均值时，发现仿真结果与试验数据的对应性较差，尤其是在转速为600 r/min的情况下。其可能是因为仿真模型中运动副摩擦参数不合理，造成了机械阻尼能耗与试验误差较大，尽管仿真输出功率的对应性较差，但在一定的误差范围内变化趋势是一致的。由图13可知，400 r/min和600 r/min的条件下其输出功率上有明显差别，这表明输出功率随着驱动轴转速的增加而显著升高。

图13 1 s工作内仿真输出功率和试验测量数据的对比

2.3.3 产品粒度分布与生产率

通过在EDEM软件中模拟产品筛分操作，提出了确定排料区的粒度分布方法。比较了400 r/min和600 r/min条件下，试验和仿真的产品粒度分布，如图14所示。试验产品的粒度最小直径为1 mm，因为仿真中元粒子的最小尺寸限制使得无法预测低于该水平的产品粒度。600 r/min的情况与实验数据的对应性较差，而400 r/min的情况与试验数据的对应性相对较好。可能是在600 r/min情况下，试验产品尺寸(-1 mm)显著增加。尽管600 r/min情况显示出很差的对应性，但在一定的误差范围内变化趋势是一致的，其结果表明600 r/min比400 r/min的破碎产品更细。

图14 仿真产品粒度分布与试验筛分结果对比

通过收集产品并计算出试验和仿真的生产率，其结果表明，在400 r/min情况下，仿真与试验结果是非常接近的，而在600 r/min情况下，可以观察到一定的差异。表5分析总结了破碎机各性能指标的仿真和试验结果，在初步建模的阶段，应该认为仿真结果在一定范围内并显示正确的趋势，则该耦合模型是成功的。

表5 仿真与试验的各性能指标分析

3 模型仿真结果及关键参数对动态性能的影响

3.1 凸锥表面点轨迹

惯性圆锥破碎机的耦合模型可以评估凸锥运动的行为，以及它与实际运动的符合程度，在全局坐标系(cxyz)0中，凸锥表面点的轨迹如图15所示。该仿真点位于凸锥表面排料口位置处，其垂直距离胶减振器上端1 000 mm，此图显示为在600 r/min的情况下，表面点的实际轨迹移动一个周期需要2.7 s，而不考虑凸锥自转则需要0.1 s。可见，凸锥自转对其表面磨损和轴承润滑起着重要作用。

图15 凸锥有无自转的仿真轨迹比较

3.2 破碎腔内颗粒流动特性

破碎腔中颗粒的流动特性决定了破碎机的生产能力。该模型也可以定性地评估粒子流动行为，例如，压碎事件中粒子动力学的假设，给出了两个随机选择的破碎颗粒的轨迹流，如图16所示。此图显示了破碎颗粒瞬间可处于三种不同的运动状态：滑动(向下)、自由下落或挤压(提升)。

图16 破碎颗粒的流动轨迹

对于惯性圆锥破碎机，根据破碎室设计、给料粒度、驱动转速和章动角，整个破碎腔的压缩事件通常近似为多个标称压缩事件。图16显示了当破碎颗粒沿轴下落时，其会产生圆周滑动，重复的曲折轨迹线表示破碎颗粒在每次标称压缩事件中被压缩或提升，然后它将滑动或自由流动到下一次标称压缩事件。在600 r/min的情况下的曲折线比在400 r/min的情况下更多，则表明在600 r/min情况下有更多的标称压缩事件，导致了产品生产率下降。

3.3 凹锥表面破碎力分布

凹锥上的破碎力分布是决定衬板磨损周期的主要因素之一，因此，通过仿真可得到凹锥表面不同区域的等效破碎力，凹锥沿z轴方向上由13个环组成，每个环有9个区域。作用在这些区域上颗粒的平均法向力表示为作用在这些区域上的破碎力Fn，且摩擦力Ft与破碎力成正比，则破碎力Fn决定了凹锥表面磨损。为了准确地预测不同位置的破碎力随时间变化，选择P31,P51,P71,P91和P111为典型位置，如图17(a)所示。图17(b)表示为在1 s内，600 r/min情况作用在典型位置的仿真破碎力，该破碎力表现出频率为10 Hz的循环行为，这与偏心激振器频率相同。仿真结果定量地预测凹锥表面的破碎力分布，表明平均破碎力和摩擦力的大小随位置数的增加而增大，因此可以将各环的材料设置为不同耐磨材料，为改善凹锥磨损周期提供了新的思路。

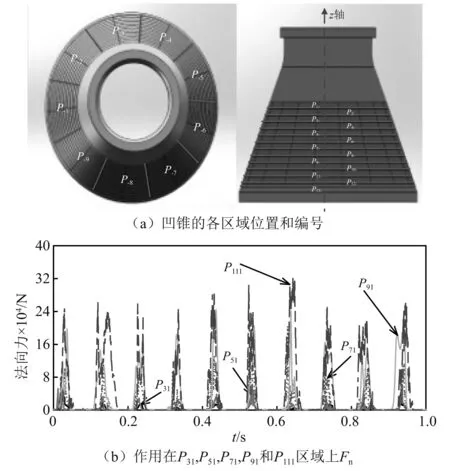
图17 凹锥面上的破碎力Fn分布

3.4 驱动转速与定锥质量对破碎机性能影响

惯性圆锥破碎机的许多参数都影响着其动态特性和工作指标，在这一节中，我们将通过仿真来讨论驱动转速和定锥质量等关键参数的影响。

3.4.1 定锥位移振幅

驱动转速和定锥质量对位移振幅影响的仿真结果，如图18和图19所示。图18表明，在相同条件下，随着转速的增加，定锥位移振幅略有升高。例如转速为由400 r/min增加到1 000 r/min时，位移振幅增大了22%，这是因为高转速给了动锥足够的偏心惯性力，增大了动锥和偏心激振器的偏心距离。

图18 定锥质量24 t下不同转速的位移振幅

图19 驱动转速600 r/min下不同质量的位移振幅

图19给出了在相同条件下定锥位移振幅与定锥质量的关系，即位移振幅随定锥质量增加而显著减小。例如质量由20 t增加到50 t时，位移振幅减小了56%，其原因是，定锥质量的增加将导致定锥在相同的破碎力下更难改变其运动状态。

3.4.2 产品粒度分布

驱动转速可以明显地影响岩石颗粒与破碎机衬板之间的动态作用，特别是影响标称压缩事件次数和岩石颗粒的局部压缩比，从而改变产品的粒度分布。驱动转速对产品粒度分布影响的仿真结果，如图20所示。

图20 定锥质量24 t下不同转速的产品粒度分布

图20给出了相同条件下的产品筛下累积粒度分布，表明驱动转速对产品粒度分布有显著影响且产品粒度将随着转速的增加而变细。这是因为高转速使给料颗粒没有足够的时间进入下一个压缩区域，则将会受到更多的破碎事件，而且也会增大局部压缩比。

图21给出在相同条件下，产品粒度分布与定锥质量之间的关系，即产品粒度将随着定锥质量增加而变细。结果表明，定锥质量在10～25 t内对产品粒度分布有一定影响，而在25～40 t内几乎没有影响。其原因可能是当振幅较大时，随着定锥质量的减小，动锥和偏心激振器的破碎力减小，进而使进料颗粒产生破碎的数量减少。

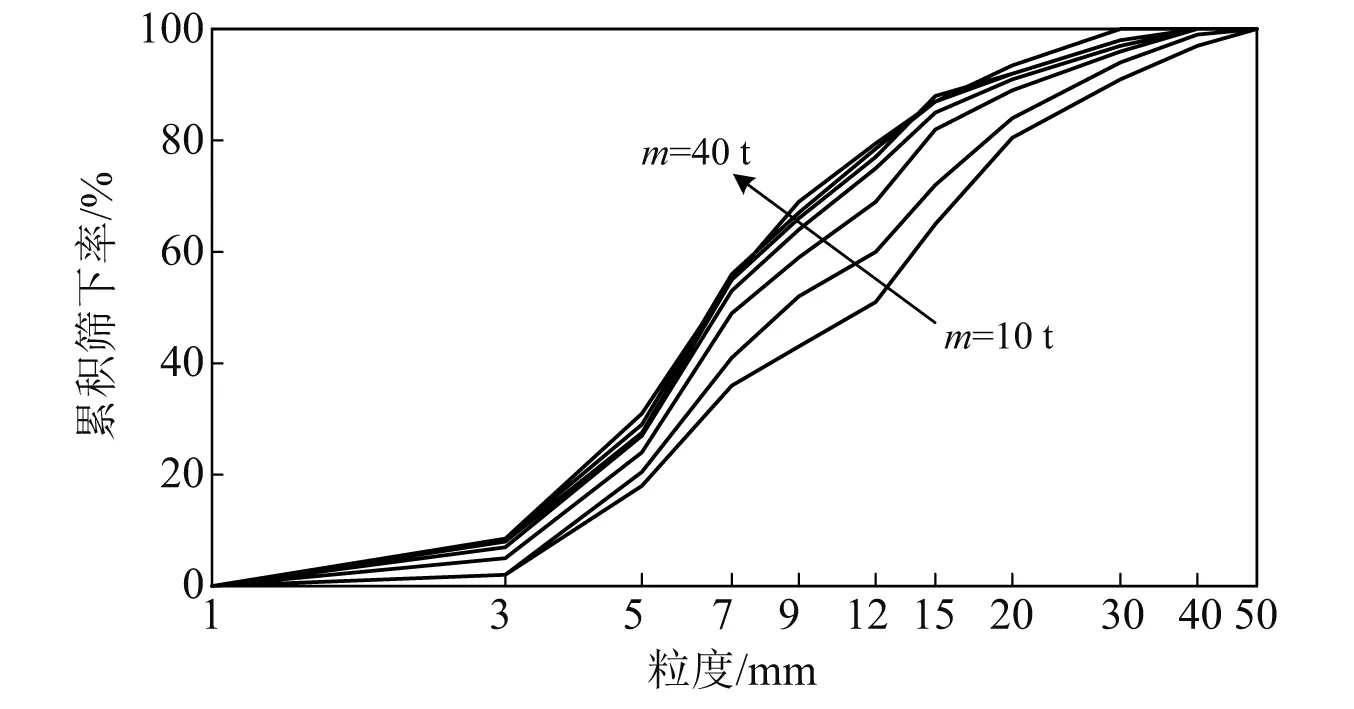
图21 驱动转速600 r/min下不同质量的产品粒度分布

3.4.3 单位能耗影响

驱动转速对功率消耗和生产率都有显著的影响，图22给出了在相同条件下，单位能耗随着驱动转速的增加而显著升高。例如转速由400 r/min增加到1 000 r/min时，单位能耗升高了近10倍，其原因是功率消耗会随着转速的增加而明显升高，且破碎产品的生产率也会随着转速增加而降低，进而造成“过粉碎”现象。

图22 定锥质量24 t下不同转速的单位能耗

定锥质量对单位能耗影响的仿真结果，如图23所示。结果表明，在5～35 t内，单位能耗随着定锥质量的增加而降低，但在35～50 t内，几乎不再降低。其主要原因是当定锥质量较大时，破碎机的振幅几乎不再改变，即破碎腔内物料颗粒的破碎事件和压缩比不再受定锥质量的影响。

根据该厂的GYP 1200惯性圆锥破碎机对破碎产品工艺指标：产品粒度小于10 mm的筛下率应大于70%，产品产量应大于50 t/h；在实际生产中应尽量降低单位能耗，因此选定驱动转速和定锥质量为优化参数。通过仿真得出，当驱动转速为600 r/min和定锥质量为35 t时，产品粒度小于10 mm的筛下率为78%，产量为64 t/h,单位能耗为1.865 kW·h/t。与工业试验600 r/min情况对比，其筛下率增加了10%，生产率增加了15%，单位能耗降低了21%并且振幅减小了40%。

图23 驱动转速600 r/min下不同质量的单位能耗

4 结 论

本文提出了一个含有黏结颗粒的MBD-DEM耦合模型来预测惯性圆锥破碎机的工作情况，该模型允许直接输入破碎过程中的主要变量，即进料量、粒度和破碎机运行参数，分析破碎机的动态性能。通过工业试验和MBD-DEM耦合仿真，对GYP 1200型惯性圆锥破碎机的性能指标进行了对比，其结果表明该耦合仿真在位移和生产率等指标方面与试验数据吻合较好，验证了模型的有效性。

根据仿真结果，定性地分析了腔内破碎颗粒的流动行为，给出了腔内破碎力分布情况，即从凹锥的进料口到排料口，其沿轴方向上的破碎力将会逐渐增大，对于改善衬板磨损具有一定参考价值。

探讨了驱动转速和定锥质量对惯性圆锥破碎机动态性能的影响。随驱动转速的增加(200～1 000 r/min)，产品粒度显著变细，但单位能耗会急剧升高，造成“过粉碎”现象；随定锥质量的增大(5～50 t)，破碎机的振幅会显著减小，但在35～50 t内，对产品粒度及单位能耗几乎没有影响。仿真表明：当驱动转速为600 r/min和定锥质量为35 t时，产品粒度和生产率分别增加了10%和15%，且单位能耗和振幅分别下降了21%和40%。该研究结果对降低惯性圆锥破碎机制造成本和优化工作参数等提供了可靠的理论依据。