风力机主轴承故障监测方法∗

郑玉巧，魏剑峰，朱 凯，董 博

（兰州理工大学机电工程学院 兰州，730050）

引言

风力机主轴承作为风力机传动系统的核心部件，承受轮毂、叶片等部件带来的多种变载冲击作用，极易发生故障［1-2］。由于风力机主轴承在距离地面几十米甚至上百米高的机舱内，一旦发生故障维护难度大、成本高，若未及时发现并解决故障会给风力机运行带来严重影响甚至造成安全事故。因此，实现风力机主轴承的故障监测，及时发现故障征兆并开展维护，对于风力机健康运行、降低运维成本具有重要意义。

传统风力机部件故障监测方法有振动分析［3-5］、声发射监测［6-7］和电气信号监测［8-9］等。其中振动监测法和声发射监测法需要安装大量的传感器来采集信号，成本昂贵；此外安装的传感器一旦发生故障，不仅导致采集的数据可靠性降低，还增加额外的运维成本。相比风力机部件的振动信号和声信号，电气信号的采集不需要额外安装传感器［10］，但电气信号中所包含的故障信息往往比较微弱，信噪比低，监测结果误差较大。因此，上述方法难以在风力机部件实际监测中大范围推广。

目前，多数风电场通过安装数据采集与监控系统（supervisory control and data acquisition，简 称SCADA）采集储存风力机各部件运行参数及环境参数，因此选择SCADA系统所记录的风力机主轴承运行参数开展其故障监测研究。主轴承故障表现形式为磨损、点蚀或塑性变形等，故障早期主轴承滚过表面损伤点产生的异常摩擦又加剧故障程度，引起主轴承温度特征的异常波动。鉴于此，本研究以SCADA系统所采集的风力机主轴承运行参数为研究对象，分别采用多元线性回归（multiple linear regression，简称MLR）、灰色模型（grey model，简称GM）及支持向量机回归（support vector machine regression，简称SVR）建立主轴承温度单一预测模型及它们的组合预测模型，引入滑动窗口方法实时监测温度预测残差的均值和标准差变化情况，通过温度预测残差均值（或标准差）的置信区间与设定临界值的对比来判断主轴承运行状态，从而实现对风力机主轴承的故障监测。

1 主轴承温度组合预测模型的构建

1.1 问题描述与数据预处理

风力机SCADA系统通常以10 min为采样周期记录并传输风速、输出功率及主轴承温度等运行参数［11］，由于风力机SCADA系统输出的各项运行参数单位不同，若直接用于建模分析对预测结果造成较大误差，因此需要对原始数据进行归一化处理，消除数据间的量纲影响。公式如下

其中：xmax为监测数据中的最大值；xmin为监测数据中的最小值；xi为原始监测值；x*为归一化处理后的数据，x*的取值范围为［0，1］。

1.2 多元线性回归（MLR）模型

MLR模型阐述一个因变量依赖多个自变量的变化规律［12］。风力机主轴承温度的变化视为多个变量参数影响下的共同作用结果，因此可将主轴承温度作为因变量（即建模输出变量），影响主轴承温度变化的运行参数作为自变量（即建模输入变量），建立主轴承温度的多元线性回归预测模型步骤如下。

设因变量（即风力机主轴承温度）为y，m个自变量（即影响主轴承温度变化的变量）分别为x1，x2，…，xm的多元线性回归方程可表示为

其中：θ0为回归常数；θ1，θ2，…，θm为回归系数。

假设在实际问题中已测得n组监测数据（yi；xi1，，xi2，…，xim）（i=1，2，…，n），则式（2）可表示为

采用最小二乘法［12］可求解得到式（3）的回归参数，将所求回归参数代入式（2）后，需要对回归方程进行统计量检验（F检验、T检验及多重共线性检验），若不满足检验要求则需要重新寻找影响主轴承温度变化的变量以便重新建模，满足要求则可直接输出模型。建模流程如图1所示。

1.3 灰色预测模型GM（1，N）

灰色模型（GM）［13］具有建模数据少、预测效果好等优点。传统的GM（1，1）模型是针对单一变量的预测，然而影响风力机主轴承温度的因素是多变量共同作用的结果，因此GM（1，N）模型更适合建立风力机主轴承温度预测模型。

由此可建立GM（1，N）模型为

其中：a为系统发展系数，反映预测值的发展趋势；bj为驱动系数，反映原始数据的内在变化。

设置参数列μ=（a，b2，b3，…，bm）T，根据最小二乘法可求解式（6）得到参数列μ的值。

对GM（1，N）模型（式6）进行白化可得

求解式（7）得到时间响应函数，表示为

最终可得累减还原式（即灰色预测值）为

1.4 支持向量机回归（SVR）模型

支持向量机回归的核心思想是建立一个最优分类面，使得所有训练样本离最优分类面的误差最小［14］。风力机主轴承温度的SVR模型的训练与预测借助LIBSVM工具箱实现。首先，选定一组风力机主轴承SCADA数据作为原始数据，对其进行归一化处理；然后，根据工具箱提供的交互检验（cross validation，简称VC）功能寻求最优惩罚参数c和核函数参数g（由函数SVMcgForRegress实现）；最后，根据得到的最优参数c，g对SVR模型进行预测。

图2 SVR算法流程图Fig.2 Flow chart of SVR algorithm

1.5 组合预测模型

假设某预测问题共有f种单一预测模型，令yt表示t时刻的实际监测值，yˆit表示第i种预测模型在t时刻的预测值（其中：i=1，2，…，f；t=1，2，…，n），第i种预测模型在t时刻的相对误差为eit

由于每种单一预测模型具有其不足之处，而组合预测模型将不同类型的单一模型按照一定的权重比例重新组合可发挥各种单一模型优势，有效削弱各种单一模型的不足以达到提高预测精度的目的。因此，建立基于熵值法［15］的组合模型，步骤如下：

1）求解第i种单一预测模型在t时刻的相对误差比重pit

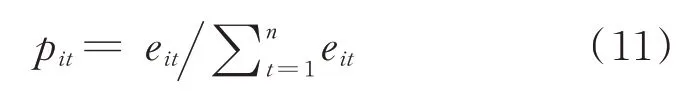
2）求解第i种单一预测模型与实际值的相对误差熵值gi

3）求解相对误差的变异系数di

4）求解各种单一预测模型的权重wi

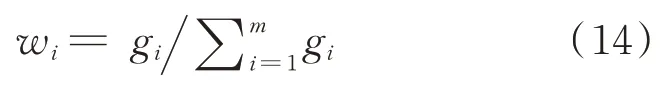
5）求解组合预测模型值

1.6 各模型综合评价指标

为实现对各个预测模型的定量评价，选取均方根误差（root mean square error，简称RMSE）、平均绝对百分误差（mean absolute percentage error，简称MAPE）、平均绝对误差（mean absolute error，简称MAE）及决定系数（R2）作为评价指标，求解公式如下

其 中：yt为 实 际 值为 预 测 值；RMSE，MAPE及MAE用来检验实际值与预测值的偏差及波动性大小，数值越小则表明预测模型精度越高；R2为自变量所解释的变化量占总变化量的比例，R2取值为［0，1］，R2越接近于1则表明预测精度越高。

2 残差统计特性分析及故障监测

2.1 滑动窗口残差统计特性分析

假设风力机主轴承温度在t时刻的实际监测值为yt，预测模型在t时刻的预测值为则预测残差序 列 为预 测 残 差序列的统计特性可由残差均值及残差标准差反映。为准确描述预测残差的统计特性（均值和标准差）变化情况，采用滑动窗口方法［16］求解预测残差序列的窗口均值及窗口标准差，滑动窗口如图3所示。

图3 滑动窗口示意图Fig.3 Schematic diagram of sliding window

设定宽度为N的滑动窗口，则窗口内的N个残差的窗口均值μ和窗口标准差σ求解公式为

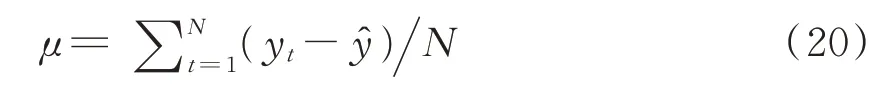
2.2 主轴承的故障监测

主轴承正常工作时，温度预测值与实际温度值接近，其残差序列分布稳定；然而主轴承发生故障会引起其温度的异常波动，进而带来预测残差统计特性的异常变化。具体表现为以下3种情况：①主轴承温度预测残差的窗口均值μ未发生较大改变，但其窗口标准差σ变化显著，残差范围增大；②主轴承温度预测残差的窗口标准差σ未发生较大改变，但其窗口均值μ变化显著，出现系统偏差；③主轴承温度预测残差的窗口均值μ及标准差σ均变化显著。

基于上述情况，可根据预测残差序列的统计特性变化来监测主轴承运行状态，设定残差均值和残差标准差故障临界值分别为μv和σv。当温度预测残差的均值或标准差超过某一临界值时，系统产生故障报警告知维护人员进行检修。假设滑动窗口的温度残差序列均值绝对值最大值为μmax，标准差绝对值最大值为σmax，则主轴承温度故障的临界标准为

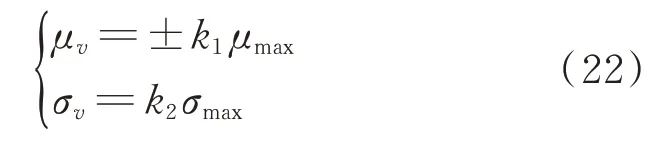
式（22）中k1，k2可由现场运维人员根据经验确定。根据预测模型对主轴承温度进行预测时，会存在各种不确定性因素对输出结果造成干扰［17］。为简化起见，将预测残差序列假设为一组均值和方差未知的正态分布数据，在求解残差窗口均值和标准差时需要给出置信度为1-α的均值和标准差的置信区间，表示为

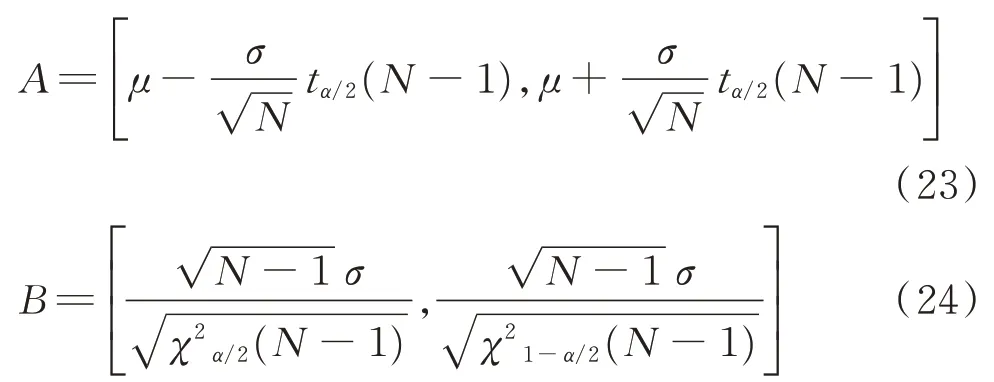
其中：tα/2为t分布的α/2分位点为χ2分布的α/2分位点，其值在给定置信度1-α后可通过查阅t分布临界值表和χ2分布临界值表得知。

当残差均值或标准差的置信区间超过各自临界值时，发出风力机主轴承故障报警信息。

3 案例分析

3.1 建模变量的选取

根据文献［18］可知，关键部件温度相关联的特征量主要包括环境温度、风速、转速及功率等，此外由于部件温度的热惯性特点使得前一时刻的部件温度对当前时刻部件温度有直接影响。因此，建立主轴承温度预测模型时初步选择风力机输出功率、风速、环境温度、主轴转速及上时刻主轴承温度作为输入变量，主轴承当前时刻温度（y）作为输出变量。

选取某风力机2019年4月主轴承正常状态时的运行参数进行建模，根据所建模型对5月份主轴承温度进行预测。按照1.1部分所述步骤对原始SCADA数据进行归一化处理，归一化后的部分数据如表2所示。

表1 SCADA数据的归一化Tab.1 Normalization of SCADA data

3.2 MLR，GM（1，N），SVR及组合预测模型的求解

3.2.1 多元线性回归模型(MLR)

以风力机输出功率（x1）、风速（x2）、空气温度（x3）、主轴转速（x4）及上时刻主轴承温度（x5）为自变量，风力机主轴承当前时刻温度（y）为因变量建立多元线性回归方程，根据1.1部分所述步骤求解得到的MLR模型为

对式（25）进行统计量检验时发现输出功率（x1）所对应的方差扩大因子（variance inflation factor，简称VIF）为15.641 8，风 速（x2）所 对 应 的VIF为15.713 4，表明所建模型存在严重的多重共线性（VIF＞10），可能会给回归结果带来较大误差，因此需要重新修正模型输入变量，以消除多重共线性。

消除多重共线性的常用方法则是剔除VIF最大值所对应的变量，即风速（x2）；剔除后的MLR修正模型自变量为风力机输出功率（x1）、空气温度（x3）、主轴转速（x4）及上时刻主轴承温度（x5），根据1.1部分所述步骤求解得到的MLR修正模型为

据检验，式（26）已消除多重共线性，F检验及T检验各项指标均满足显著性条件。利用修正后的MLR模型对5月份主轴承温度进行预测，部分预测值及残差值见表2。

表2 MLR模型部分温度预测结果值Tab.2 Temperature prediction results of MLR model℃

3.2.2 灰色预测模型GM(1,N)的求解

基于MLR修正模型所得自变量及因变量，选择当前时刻主轴承温度、功率、空气温度、主轴转速及上时刻主轴承温度的时间序列为原始数据序列其中：当前时刻主轴承温度数据序列为系统特征数据序列；而功率数据序列空气温度数据序列主轴转速数据序列以及上时刻主轴承温度序列均为相关因素序列。选取2019年4月份SCADA数据依据1.2所述步骤进行建模，求解得到GM（1，N）模型参数列μ的值为

μ=(2.014 5，-0.000 6，0.062 5，0.146 5，1.972 3)T

将参数列μ代入式（8），得到时间相应函数，而后根据式（9）累减可得到GM（1，N）预测值，部分预测值及残差见表3。

表3 GM(1,N)模型部分温度预测结果值Tab.3 Temperature prediction results of GM(1,N)model ℃

3.2.3 支持向量机回归模型(SVR)的求解

基于MLR修正模型所得自变量及因变量，选择2019年4月份的当前时刻主轴承温度、功率、空气温度、主轴转速及上时刻主轴承温度等序列数据用来训练SVR模型，用训练好的模型来预测5月份主轴承温度值。

给定参数c和g的初始范围均为［-8，8］，根据交互检验法求解得到SVR模型最优参数c和g为：Bestc=1.414 2，Bestg=0.353 5；根据所求最优参数c和g对SVR模型进行训练，然后对5月份数据进行预测，部分预测值及残差值见表4。

3.2.4 MLR、GM(1,N)及SVR组合模型的求解

假设MLR修正模型所得主轴承温度预测值为yˆ1t，GM（1，N）模型所得预测值为yˆ2t，SVR模型所得预测值为则应用熵值法确定的各模型最优权重为w1=0.125 8，w2=0.310 5，w3=0.563 7，因此可得组合模型表达式为根据所求组合模型对5月份数据进行预测，部分预测值及残差见表5。

表4 SVR模型部分温度预测结果值Tab.4 Temperature prediction results of SVR model℃

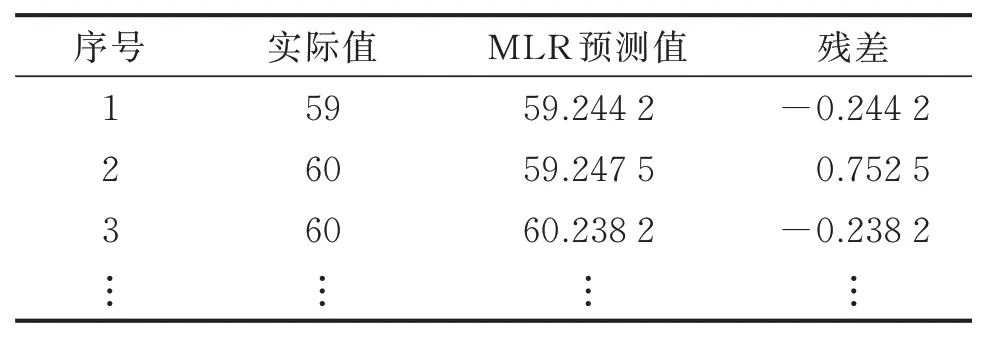
表5 组合模型部分温度预测结果值Tab.5 Temperature prediction results of Combined model ℃

3.3 各模型预测结果对比分析

根据各模型对5月份主轴承温度数据进行预测，实际值与各模型预测值变化趋势如图4所示。

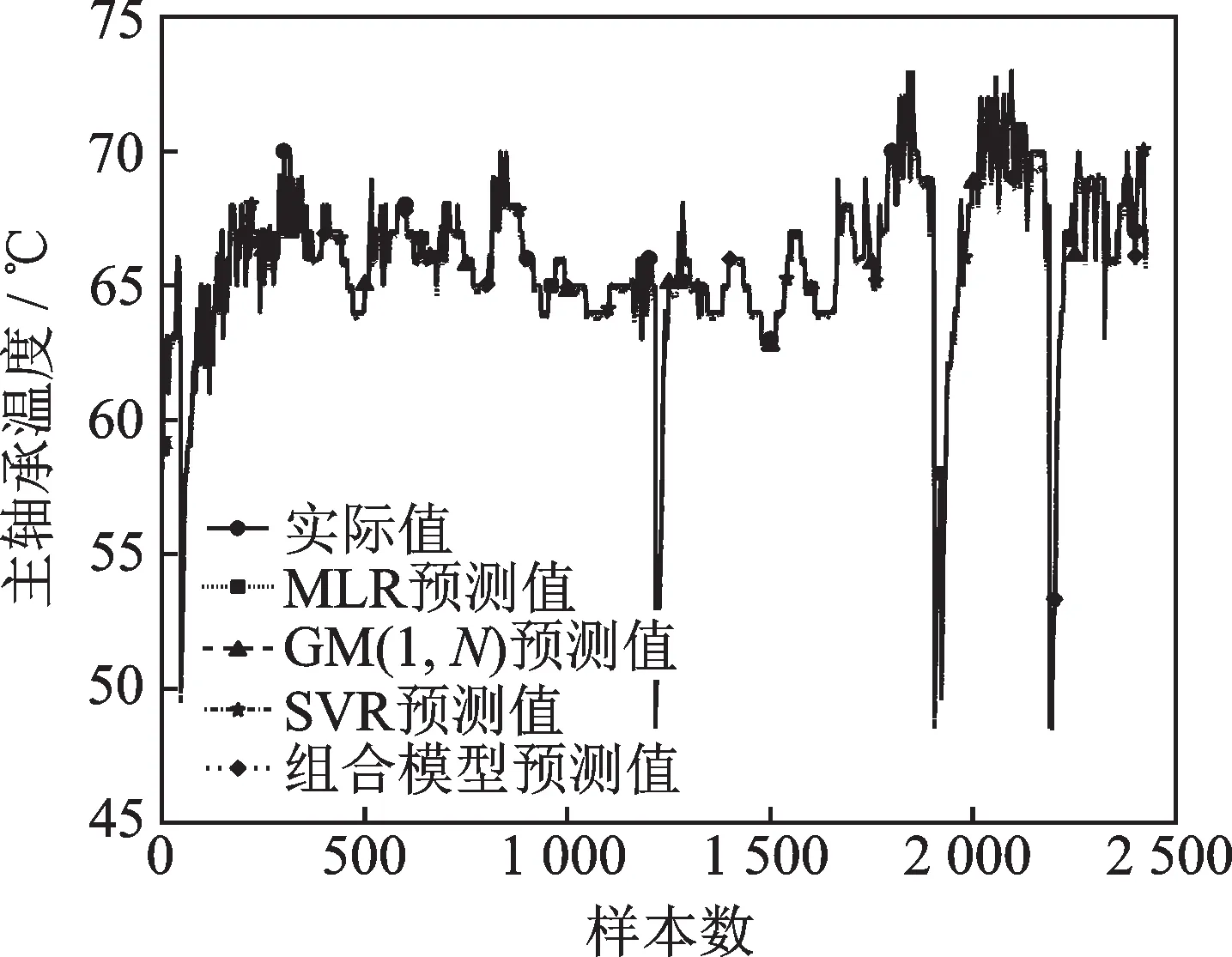
图4 风力机主轴承温度预测图Fig.4 Forecast figure of wind turbine main bearing temperature

图4 显示在第48，1 220，1 928及2 206点附近处主轴承温度较低，查询主状态日志可知是由于风力机停机重新启动所造成。另外从图中可看到，不同模型所求主轴承温度预测值与实际值变化趋势相近，拟合程度较高；但根据图4不易直观判断哪种模型预测值与实际值吻合度更好。为进一步对比各模型优劣性，进而求解各模型综合评价指标值，见表6。

表6 各模型指标对比值Tab.6 Comparison results of each model index

由表5的各指标数据对比可知，组合模型的RMSE，MPE及MAE最小，R2最大，表明组合模型偏差及波动性更小，在各模型中具有最高的预测精度；其中组合模型的R2值分别较其他模型提高0.049 3，0.002 7和0.000 2。因此，选择在组合预测模型基础上引入滑动窗口方法实现对风力机主轴承的故障监测。此外在单一预测模型中，SVR模型具有良好的预测精度，各项指标均和组合模型指标相近。

3.4 基于滑动窗口的主轴承温度故障状态监测

查询风力机主状态日志可知，5月份风力机主轴承未发生故障。为验证方法有效性，人为模拟主轴承因发生故障而导致主轴承温度升高的情况。选择5月份主轴承温度较高的12～15号3天累计568个温度点进行研究，取滑动窗口宽度N=20，置信水平α=0.05，根据式（23），（24）求解得到主轴承正常状态下预测残差均值及标准差的各自95%置信区间，它们的变化趋势如图5所示。

图5 残差窗口均值和标准差Fig.5 Residual window mean and standard deviation

图5 （a）为主轴承温度残差窗口均值变化趋势图，从图5（a）可知主轴承温度残差窗口均值最大值为μmax=0.223 5（即A点）；图5（b）为主轴承温度残差窗口标准差变化趋势图，由图5（b）可知主轴承温度残差窗口标准差最大值为σmax=0.764 6（即B点），由于是人为模拟故障，所以残差标准差并未发生变化。故选择残差窗口均值展开分析，取k1=2，则窗口均值临界值根据式（22）可得μv=±0.447 0。

从第303个温度点开始人为加入步长为0.015℃的温度累积偏移量，基于组合模型的主轴承温度预测残差均值变化趋势如图6所示。

图6 模拟故障状态的残差窗口均值Fig.6 Residual window mean value of simulated fault state

图6 显示，主轴承正常运行时残差均值95%置信区间均未超过临界值，在C点即第284个窗口（303-20+1）加入温度偏移后，滑动窗口残差均值逐渐增大，在D点残差窗口均值95%置信上界超过临界值0.447 0，引发主轴承故障报警。综上可得，当主轴承发生故障导致其温度异常时，基于滑动窗口方法的故障监测方法可及时发现故障并报警，有效监控主轴承异常状态。

4 结束语

基于风力机SCADA数据分别建立主轴承温度的MLR，GM（1，N），SVR 3种单一预测模型及它们的组合预测模型；其中组合模型有着更优越的预测性能，其决定系数分别比其他模型提高0.049 3，0.002 7及0.000 2。此外SVR模型在单一预测模型中有着更高的预测精度。在组合预测模型基础上引入滑动窗口方法求解分析温度预测残差的统计特性（均值和标准差），当窗口均值或标准差的置信区间超过设定临界值时可判断出主轴承发生故障，有效监测主轴承运行状态。笔者所提方法可用于工程实际中风力机或其他机械设备的关键部件温度预测及故障监测。