Lamb波波包混叠分离方法的结构损伤定位∗
2021-04-28季宏丽吴义鹏裘进浩
郭 禹,张 超,季宏丽,吴义鹏,裘进浩,王 勇
(1.南京航空航天大学机械结构力学及控制国家重点实验室 南京,210016)
(2.上海宇航系统工程研究所结构系统研究室 上海,201109)
引言
结构健康监测(structural health monitoring,简称SHM)是一种实时、在线的监测技术,通过获取与结构损伤相关的多种参数,识别结构中存在的损伤,进而预测结构的使用寿命,防止损伤的扩展,减小安全事故发生的概率[1-3]。在众多SHM技术中,Lamb波能够在大尺度板状结构中远距离传输,信号的衰减量小,并且对于结构中的损伤具有很高的灵敏度,因此被广泛用于损伤监测[4-6]。
在基于Lamb波的损伤监测技术中,主要有损伤因子监测技术和利用损伤因子进行损伤成像的监测技术。损伤因子旨在提取结构在时域、频域、时频域及波数域的特征变化来衡量结构的健康状态[7-9]。而损伤成像技术通过成像的方法表征结构中的损伤,快速地确定损伤在结构中的位置。因为损伤成像直观、损伤信息多等优点,成为了许多学者研究的热点。Wang等[10]提出了时间反转成像法(time-reversal method,简称TR),通过时间反转并重新激发传感器阵列采集到的信号完成损伤的聚焦成像。这种方法不需要提前知道结构的基线信号就可以完成损伤定位。Zhao等[11-12]研究了损伤概率重构(reconstruction algorithm for probabilistic inspection of defects,简称RAPID)的方法,计算不同信号对于损伤位置的概率的贡献度,重构出损伤的位置。Michaels等[13]使用时间延时-累加定位法精准地定位了铝板上的缺口和腐蚀损伤,延时-累加(delay-andsum,简称DAS)定位法基于残余信号的理论波达时间完成对损伤的定位成像。
对于复杂结构和传感器距离边界较近的情况,损伤散射的Lamb波遇到边界会产生反射,实际得到的残余信号会出现多个波包叠加的情况。当损伤靠近边界时甚至会发生损伤信号和边界反射波包混叠的情况,从而导致DAS定位法出现偏离和伪损伤。Shan等[14]针对复杂结构的DAS定位提出了一种自适应有效数据提取的方法,自适应地截取信号的波包来提高DAS定位的精度。然而当损伤散射波包和反射波在时域上重叠时,直接截掉反射波的同时也会截断大部分的损伤波包时域信号,导致定位结果变形。在成像损伤误判的问题上,Sharifkhodaei等[15]提出了一种改进的延时-累加方法(windowed energy arrival method,简称WEAM),对残余信号能量的包络加上对数正态分布窗函数来捕捉首个波峰作为损伤的实际散射信号,从而提升DAS成像的精度。James等[16]提出了最小方差无失真响应的方法,通过给传统的DAS定位增加加权系数来减少噪声的投影。Lu等[17]使用边界反射系数来减少边界反射信号造成的伪损伤投影,反射系数由换能器的分布和反射信号的强度来决定。但是这些方法都没能完全提取信号中的反射波波包。另一方面,Lamb波由于频散效应会使得波包变宽,时域信号会产生变形,如果直接使用残余信号进行延时-累加定位,将使得损伤区域面积变大,降低定位的精度。传统的信号处理方法,如希尔伯特变换、黄氏变换、短时傅里叶变换和小波变换都不能对Lamb波进行频散补偿。
针对以上反射波混叠和Lamb波频散补偿的问题,笔者研究了Lamb波波包混叠分离的结构损伤定位方法,提升DAS定位算法的成像精度。首先,对复杂边界条件下反射波和损伤散射波混叠的问题,建立了含频散效应的Lamb波波包混叠和函数模型;其次,提出了基于隐变量参数求解的波包分离方法,重构了每个波包的分布情况,消除了反射波投影引起的传统DAS定位中的伪损伤;然后,对重构出的每个波包进行了频散补偿,抑制了波包随传播距离产生的变形,提高了定位成像的分辨率;最后,在飞机复合材料加筋壁板上实验验证了改进DAS方法的可靠性。从结果来看,波包分离法能够解决反射波混叠和频散补偿的问题,提升损伤定位的精度。
1 含频散效应的Lamb波波包混叠模型
Lamb波信号vac(t)会因为传播时间变化发生频散,导致波包参数发生改变。激励信号vac(t)为高斯窗调制的窄带信号,vac(t)的频域表示为Vac(f)
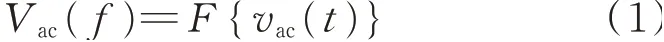
其中:F为傅里叶变换。
不同波达时间τk的Lamb波波包信号的频域和时域表达式为
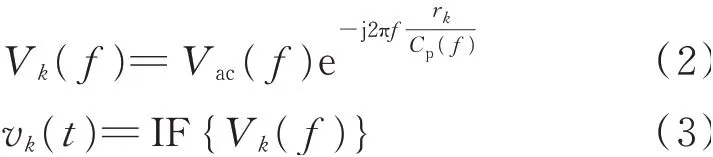
其中:IF为逆傅里叶变换;rk为波达时间τk下Lamb波的传播距离;Cp(f)为A0模式的相速度。
通过复Morlet小波ψ(t)提取频散后信号vk(t)的包络Φk(t)为
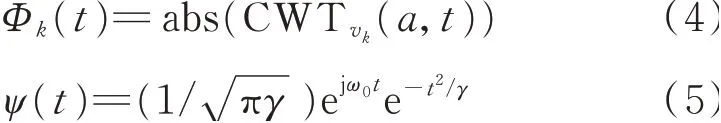
其中:ω0为小波的中心角频率;γ为高斯宽度;abs为取模;a为尺度因子;CWT为小波变换。
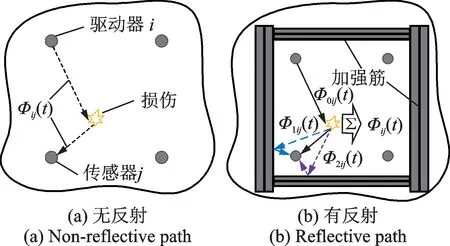
图1 残余信号在无反射、有反射下的传播路径Fig.1 The residual signal in the non-reflective and reflective path
在不考虑边界的板结构中(如图1(a)所示),驱动器i到传感器j之间的损伤散射信号包络为Φij(t)。然而,在典型的航空加筋结构中(如图1(b)所示),加筋引起残余信号的反射,导致获取的残余信号Φij(t)中包含多个不同时延的损伤反射波包。实际的损伤散射信号Φij(t)是由直达波Φ0ij(t)和后续的反射波AkΦkij(t)混叠而成,如式(6)所示
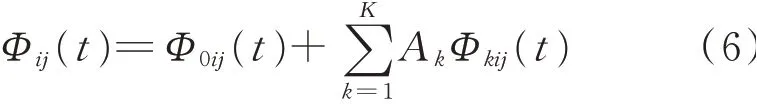
其中:Ak为第k个反射波信号幅值系数;Φkij(t)为波达时间τk的反射波信号;实际的包络信号Φij(t)为含频散效应的Lamb波波包和函数。
在延时累加算法中,每个点(x,y)的像素值I(x,y)由散射信号包络Φij(t)在延时tij(x,y)之后得到,tij(x,y)是任意位置散射点(x,y)在驱动器(xi,yi)到传感器(xj,yj)路径上的理论传播时间,表达式为
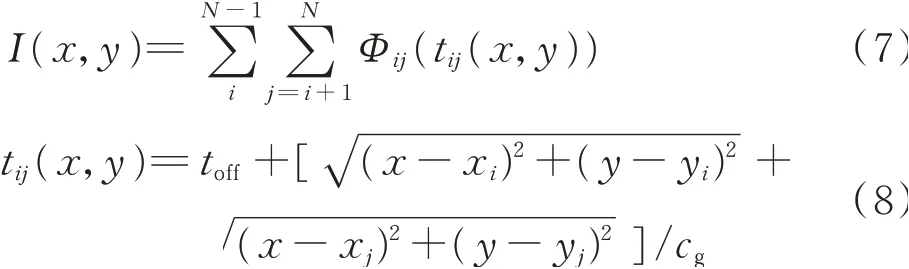
其中:N为监测区域内的传感器数量;toff为激励偏置时间;cg为群速度。
混叠的时域信号投影到定位图上会对定位结果产生影响。针对该问题,文献[14]中采用了如下的自适应提取的方法对信号Φ进行截取,信号长度表达式top为
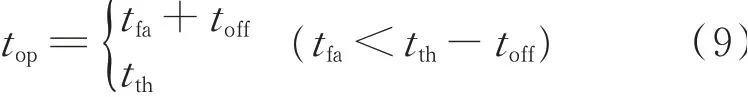
其中:tfa为首波峰的时间;tth为信号截取阈值。
但是直接截取不能有效地分离混叠的波包,需要对混叠波包函数Φij(t)进行解耦分离。
2 波包分离方法及数值验证
2.1 含频散效应波包的高斯拟合
以厚度为1 mm的碳纤维复合材料板为例,考虑A0模式的相速度曲线(如图2所示),根据式(2)和(3)可以计算得到不同波达时间τk的Lamb波波包信号,如图3所示。其中:图3(a)为50 kHz的窄带激励下的响应信号,波达时间最大为850μs;图3(b)为对应信号的包络Φk(t),τk越大,信号包络越宽。激励的窄带信号vac(t)的表达式为
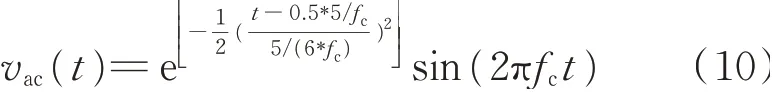
其中:fc为激励信号的中心频率。
由式(10)可知,窄带信号vac(t)是由高斯窗调制的,采用式(4)中的小波变换,可以推得激励信号的包络Φac(t)是一个严格的高斯函数
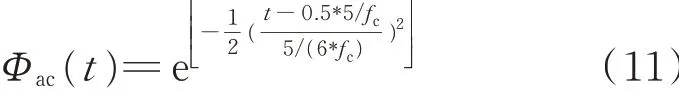
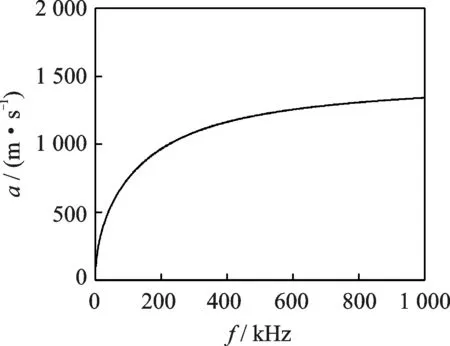
图2 碳纤维复合材料板A0模式相速度曲线Fig.2 A0 mode phase velocity curve of CFRP panel
因此采用高斯函数对频散后的波包信号进行拟合重构。单个波包的波达时间τk已知,用方差σk2来表示Φk的宽度,拟合的表达式为
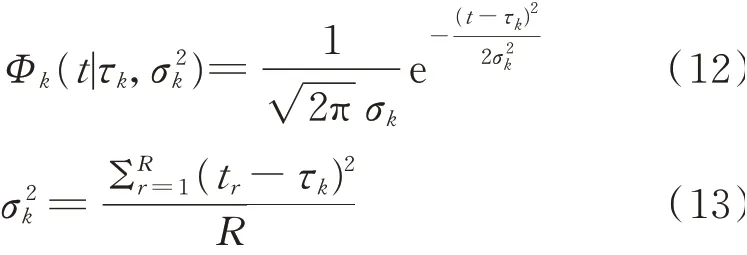
其中:tr为信号Φk(t)的样本;R为样本数;τk为高斯函数的均值。
重构得到的频散波包的包络(如图3(c)所示)和原始信号的包络一致,并且前后包络信号的相对平均误差不超过0.1%,完成对单个频散波包参数的估计。
波包的宽度随波达时间的增大而增大,对波达时间τk=[50∶1∶1 000]μs的序列进行方差σk2的拟合,得到如图4所示的差值函数σk2=σ(τk)2。代入式(12),单个频散波包的函数式Φk=Φk(t|τk)只由参数波达时间τk决定。混叠波包模型Φ的表达式为
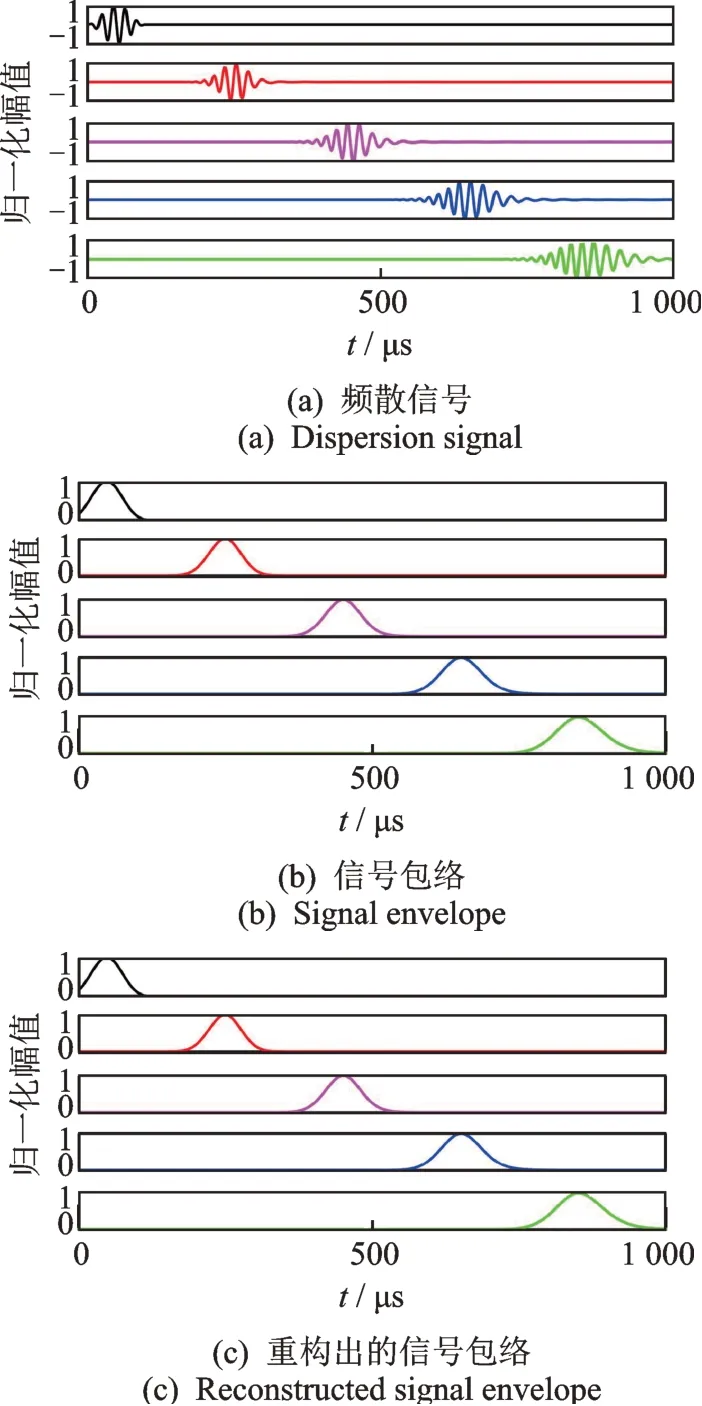
图3 不同波达时间Lamb波Fig.3 Lamb wave at different arrival times
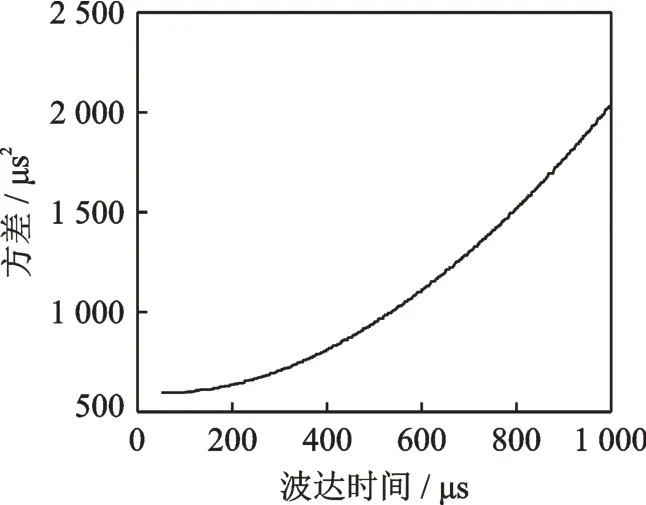
图4 方差关于波达时间的插值函数σk2=σ(τk)2Fig.4 Interpolation functionσk2=σ(τk)2 of variance on arrival time
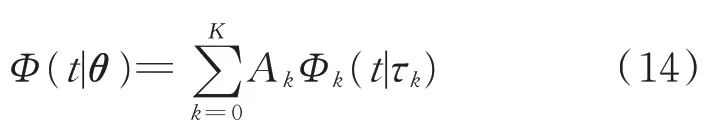
其中:θ=(A,τ);A=(A0,…,A k,…,AK);τ=(τ0,…,τk,…,τK)。
2.2 波包函数的分离补偿方法
为了识别出波包混叠函数Φ对应最优的参数项θ=(A,τ),将模型的对数似然函数L(T|θ)作为优化的性能参数目标。对数似然函数L(T|θ)的计算公式为
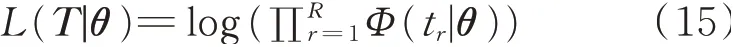
其中:T={t1,…,tr,…,tR}为信号Φ(t)对应的样本集。
采用隐变量迭代估计的方法求解极大似然估计L,输入参数θ(0)=(A(0),τ(0))通过K-mean算法对样本集T初始化得到,θ(0)作为第0次迭代的参数[18-19]。其中波包信号样本T表示给定观测变量的数据,此时反映观测数据tr来自分波包函数Φk的数据是未知的,用隐变量zrk表示,其定义为
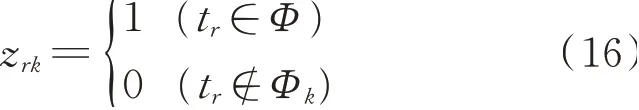
其 中:zrk组 成 隐 随 机 变 量 的 数 据Z={z10,…,zrk,…,zRK}。
T和Z连在一起称为完全数据,得到完全数据下的对数似然函数L*为
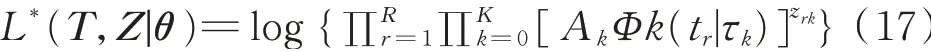
已知初始参数θ(0)后,每一次迭代的求解都分为E步和M步[20]。E步需要确定Q函数Q(θ,θ(l)),即完全数据下的对数似然函数L*关于观测变量T和第l次 迭 代 的 参 数θ(l)下 对 未 观 测 数 据Z的 期 望,由式(17)得到
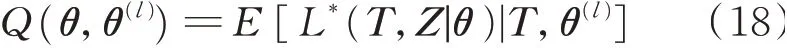
其中:E为对Z的数学期望。
迭代的M步是求解在θ(l)下Q(θ,θ(l))对θ的极大值,得到新一轮的迭代的模型参数为
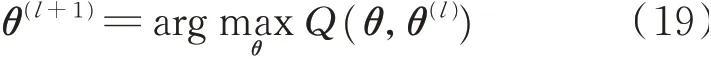
重复以上迭代,直到式(19)中对数似然函数L的相对变化量小于一个极小值β。L(l)为第l次迭代的对数似然函数的值,L(l+1)为第l+1次迭代的值。收敛条件为
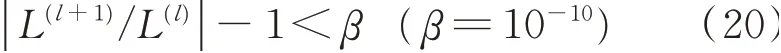
通过最终收敛的参数θ重构出的每个波包函数Φk,随着τk的增加,波包的宽度也在增加。此时根据图4中得到的方差的插值函数σk2=σ(τk)2,定义频散补偿系数为
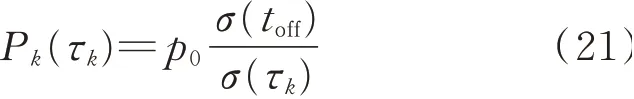
其中:σ(τk)为τk对应的标准差;σ(toff)为激励信号的标准差;p0为固定频散补偿系数。
补偿后的波包函数Φk的表达式为
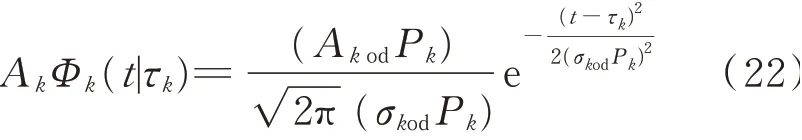
其中:Akod和σkod为补偿前的参数。
从Φk中筛选重组出原本信号Φ的直达波包Φ*,计算公式为
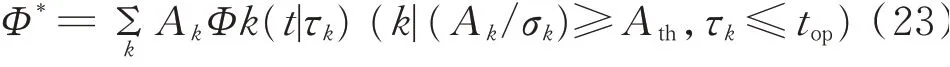
其中:Ath用来控制幅值的阈值,为信号包络最大值Amax的0.5,筛选出能量较大的波包;top为控制波达时间的阈值,通过文献[14]中自适应截取信号长度的方法计算得到(如式(9))。
筛选出波达时间较早的波包,得到分离反射波后的直达波波包Φ*。而式(9)中的阈值tth的计算公式为

其中:rmr为以阵列对角线为长轴且经过长边中点椭圆的监测距离;cg为波的群速度。
2.3 Lamb波波包分离方法的数值验证
为了验证波包分离法对于混叠波包信号的重构效果,对数值模拟的混叠Lamb波信号进行波包分离重构。激励的信号选取50 kHz的窄带信号。随机生成图5(a)中6个不同波达时间τk和幅值系数Ak的Lamb波信号。由式(4)小波变换求解得到各个波包的原始信号包络分布如图5(b)所示。将图5(c)中信号包络对应的观测样本T作为算法的输入,计算样本的初始最大似然估计L(0)和新一轮的模型参 数θ(1),然 后 计 算 参 数θ(1)对 应 的 最 大 似 然 估 计L(1),直到重构参数θ(l)对应的L(l)收敛。
由最终重构得到的参数θ,得到分离后的波包分布Φk如图5(d)所示。重构后的波包分布收敛于正确的波包初始参数,成功对混叠波包信号Φ实现了分离。
对比多组不同情况下的随机仿真信号,对比输入的混叠波包参数θ和分离重构得到的波包参数θ。重构前后参数θ=(τ,A)的多组误差的平均值如表1所示。算法前后重构得到参数的误差都在5%以内,波包分离法的参数估计的可靠性较好。
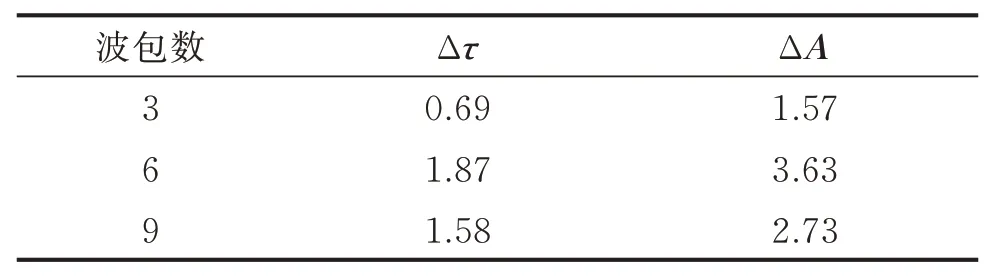
表1 重构前后参数θ的误差Tab.1 Error of parameterθafter reconstruction %
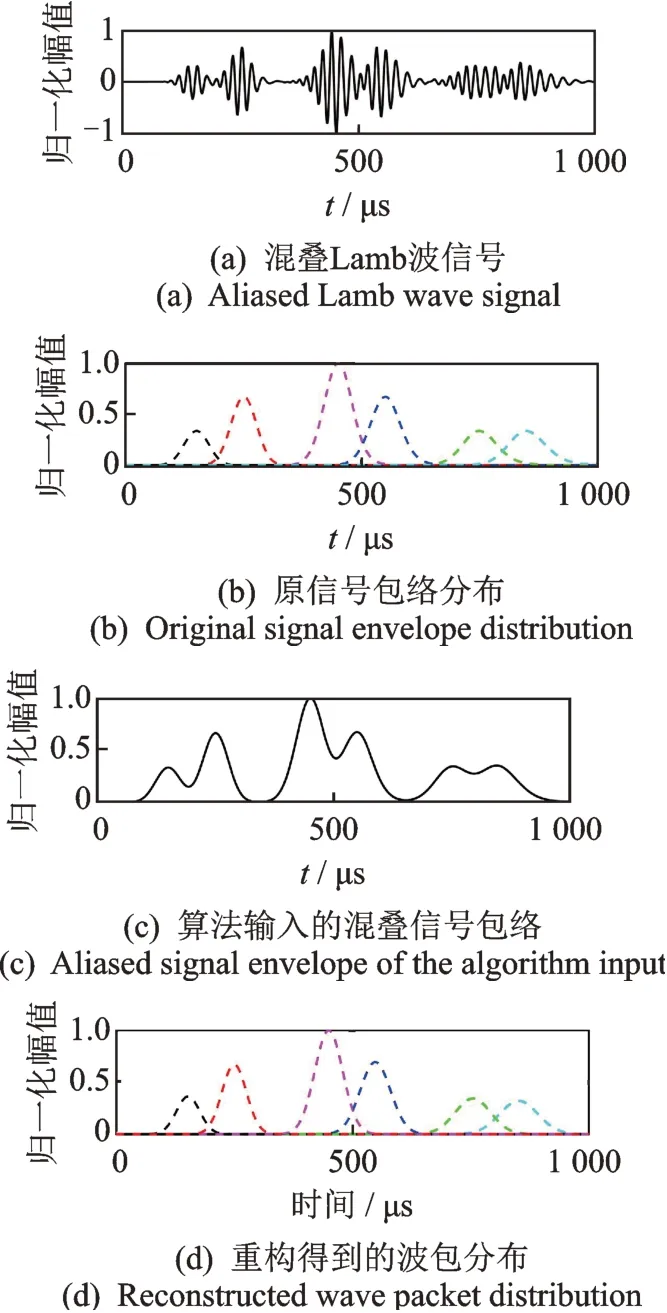
图5 波包分离的数值验证Fig.5 Numerical validation of wave packet separation
3 实验验证
3.1 实验建立
实验的对象是飞机复合材料加筋壁板(如图6所示)。结构尺寸为950 mm×1 000 mm×1 mm,8层纤维的铺层方向是按照[0°/90°/45°/-45°]S的顺序排布的。图6展示了实验的监测系统。其中NI-PXI-5412发波卡用于产生激励信号,通过Trek-2100HF功率放大器给到通道切换电路,NI-PXI-5105采集传感器的信号。
实验中选择的监测区域为图6中ABCD四传感器阵列围成的虚线区域。监测区域的尺寸为220 mm×130 mm,传感器距离加强筋边界的距离小于40 mm,响应信号包含验证的Lamb波反射。激励信号选用的是窄带5波峰信号。激励中心频率fc为50 kHz。在该频率下,Lamb波的A0模式在信号中占据主导地位,其他模式的信号可以忽略不计。激励信号通过功率放大器放大到50 V作用在复材加筋板上,每个通道的采样频率为1 ms/s。单损伤和双损伤的半径为10 mm,采用吸波介质来模拟孔状损伤。
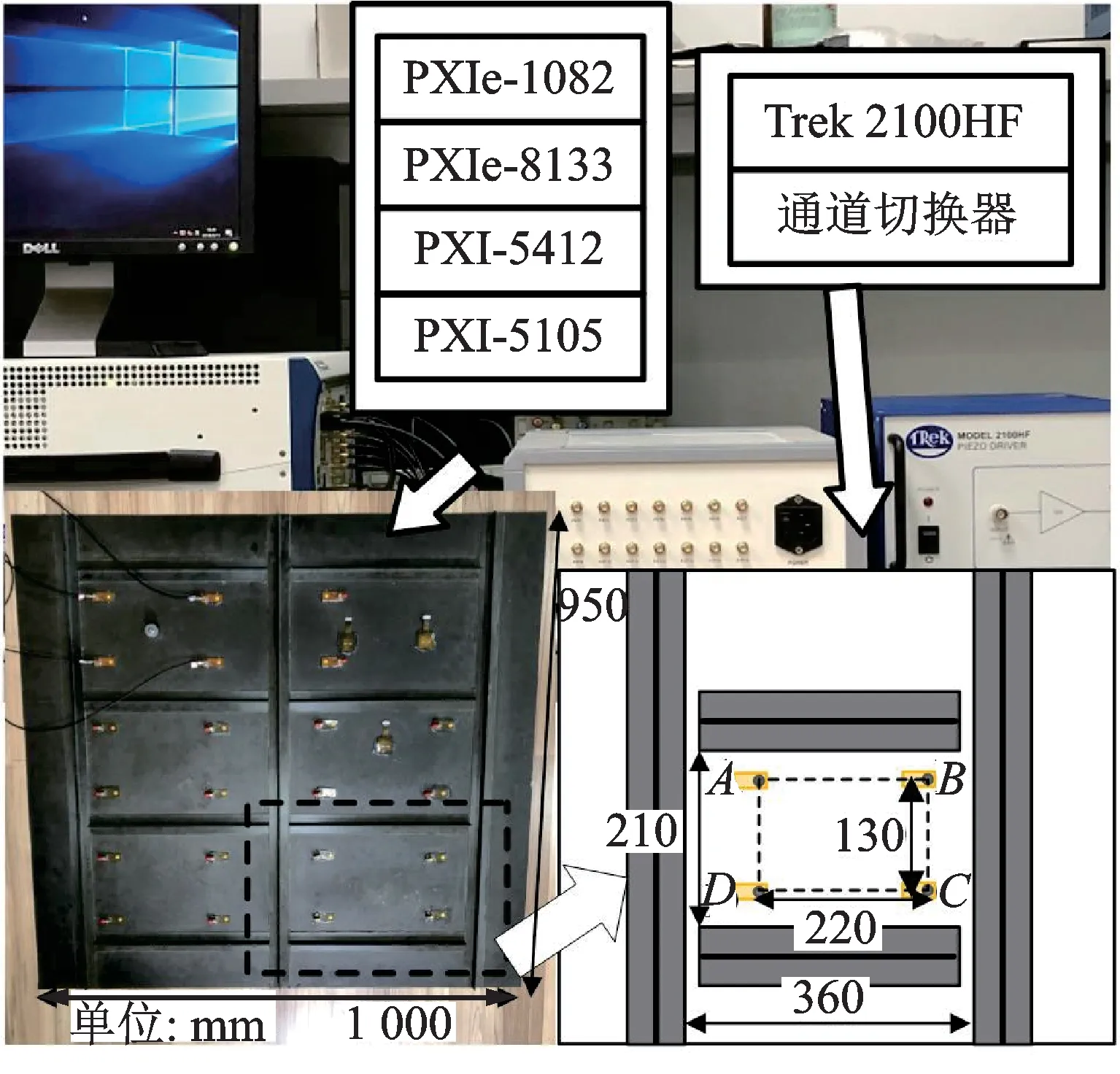
图6 实验系统和结构Fig.6 Experimental system and structure
3.2 单损伤实验结果
在单个损伤的情况下,对监测区域ABCD进行扫描监测。传感器B和C之间残余信号的串扰部分已经置零(如图7(a)所示)。利用传统DAS定位方法(将波包信号带入式(7)),残余信号的包络Φ(t)(如图7(b)所示)投影得到的损伤定位结果如图8(a)所示。其中:白色符号“×”表示损伤实际的位置;黑色符号“+”表示伪损伤的位置。损伤的实际位置是坐标(75,45),对应时域信号中330μs处的直达波。伪损伤的位置发生在左下角(40,0)上,伪损伤对应图7(b)时域信号中400μs左右的强反射波。反射波的幅值甚至超过了直达波的幅值,导致定位结果在(40,0)处出现了伪损伤。
采用文献[14]中自适应提取信号的方法,计算得到信号长度为380μs,截取时域信号波包(如图7(b))。由于直达波(330μs)和反射波混叠(400μs)的原因,截取的残余信号中仍包含一部分反射波(400μs),并且截取了混叠信号中的直达波信号,在带入DAS算法(式(7))投影后,破坏原有的定位结果(如图8(b))。
将图7(b)中的残余信号波包Φ(t)的样本T作为算法的输入,对波包进行隐变量概率模型重构,得到波包函数Φ的分布,并对分离后波包进行频散补偿,得到分离补偿之后的各个波包分布(如图7(c))。根据边界距离设置反射波达到的时间阈值,最终分离反射波后得到直达波波包Φ*(图7(d))。在对时域信号波包进行波包分离和频散补偿之后,得到定位结果如图8(c)所示。定位结果在(75,45)左右与实际损伤位置符合,像素图只有直达波包(330μs)对应的投影,这是因为分离了反射波包(400μs),所以消除了波包在定位图上(40,0)处的投影。另一方面,由于频散效应得到了一定的补偿,损伤定位图的分辨率得到了提高。
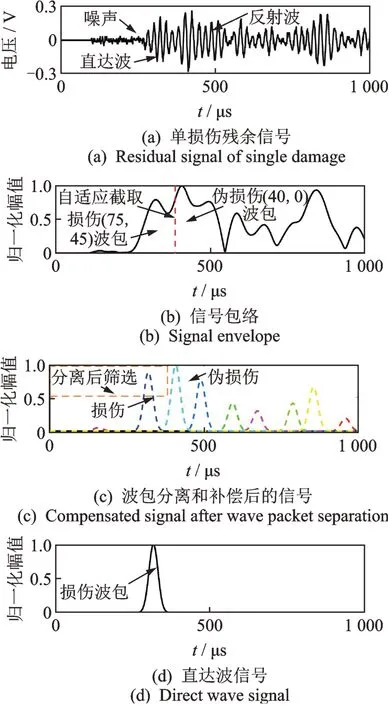
图7 单损伤传感器路径B-C间波包分离Fig.7 Wave packet separation of single damage on sensor BC path
Lamb波波包混叠分离方法的目的是为了消除反射波的成像投影和频散补偿,提升定位成像的信噪比和空间分辨率。为了定量评估损伤定位成像的效果,定义了损伤图像的信噪比SNR(dBs)为
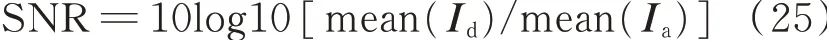
其中:变量mean(Id)和mean(Ia)分别为损伤定位图在实际损伤区域和健康区域内的图像强度均值。
SNR的效果和信号处理、图像处理中的一样,SNR的值越高代表损伤图像的分辨率越高,定位噪声越小。
在单损伤的情况下,原始图像对应的mean(Id)为0.953,mean(Ih)为0.586,得到波包分离前的信噪比SNR为2.11。改 进的DAS方 法 中,mean(Id)为0.920,mean(Ih)为0.413,得到SNR值为3.48。选取不同位置的5组损伤进行成像,得到的损伤图像信噪比如表2所示,损伤定位成像的结果得到了提升。
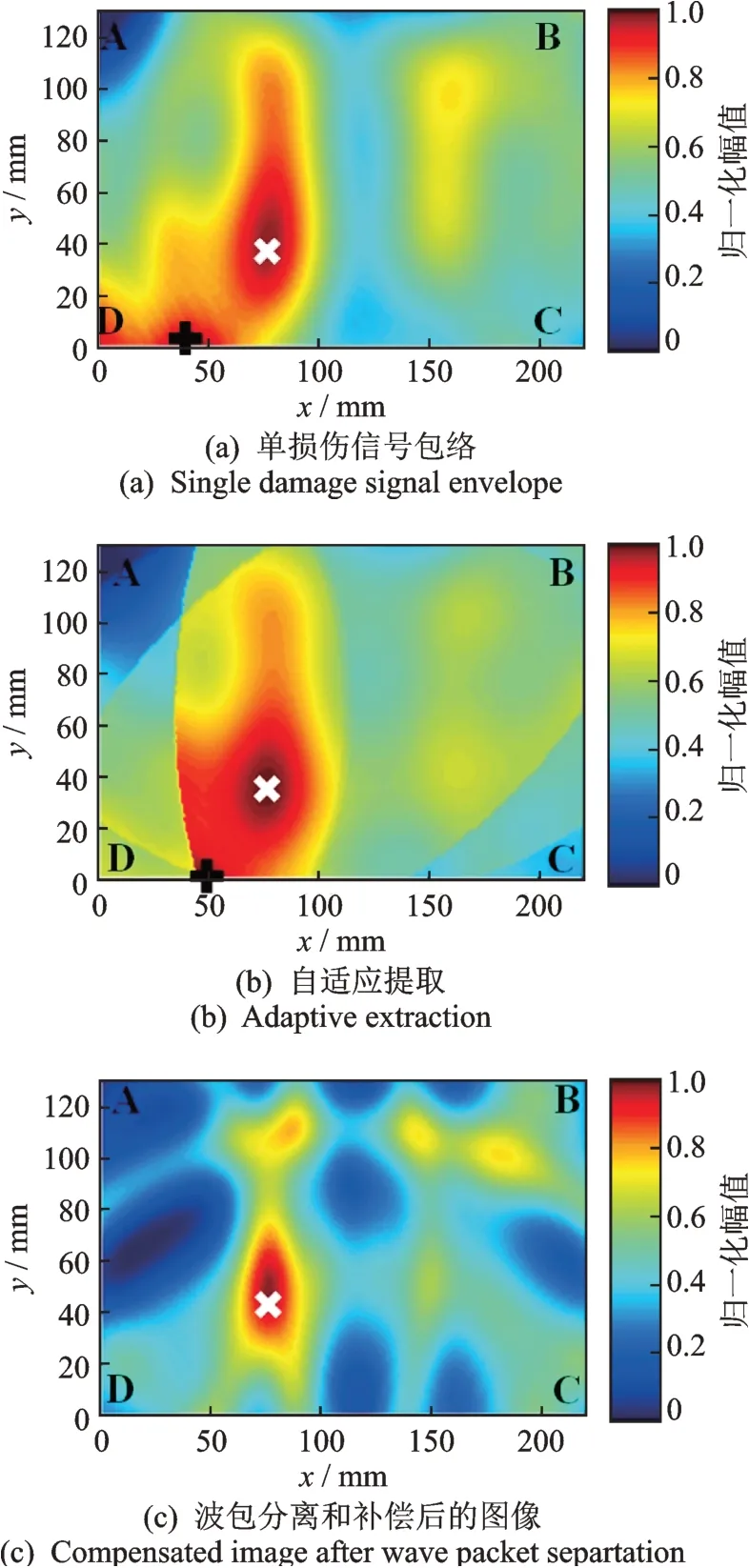
图8 单损伤信号定位结果Fig.8 Localization result of single damage signal
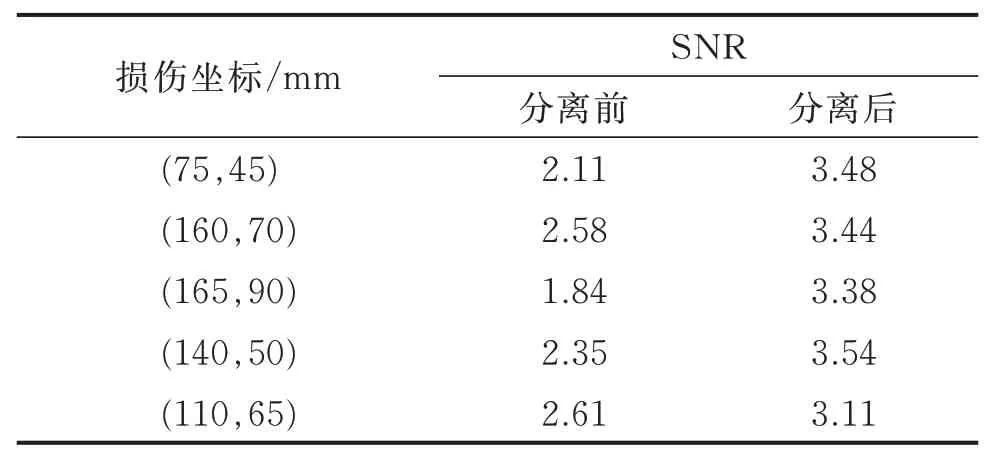
表2 损伤成像评估Tab.2 Damage imaging assessment dB
3.3 双损伤实验结果
对监测区域ABCD进行双损伤定位实验,损伤的实际位置在(150,90)和(140,30)。图9(a)中的残余信号在传感器B和C之间,两个损伤的散射波包的波达时间分别在200和220μs左右,由于波达时间距离太近,在时域上出现了大面积重叠。对双损伤包络信号Φ(t)定位的结果如图10(a)所示,损伤的实际位置在(150,90)和(140,30)(对应200和220μs)。然而,相比于损伤1,损伤2的幅值由于分辨率太低,难以从健康区域的幅值中突显出来。从时域信号上看,图9(b)中2个损伤在时域上的波包距离非常近,受到频散影响,残余信号的波包变宽,时域中波包重叠量大,时域信号投影到像素图中只有1个峰,导致了损伤的丢失。
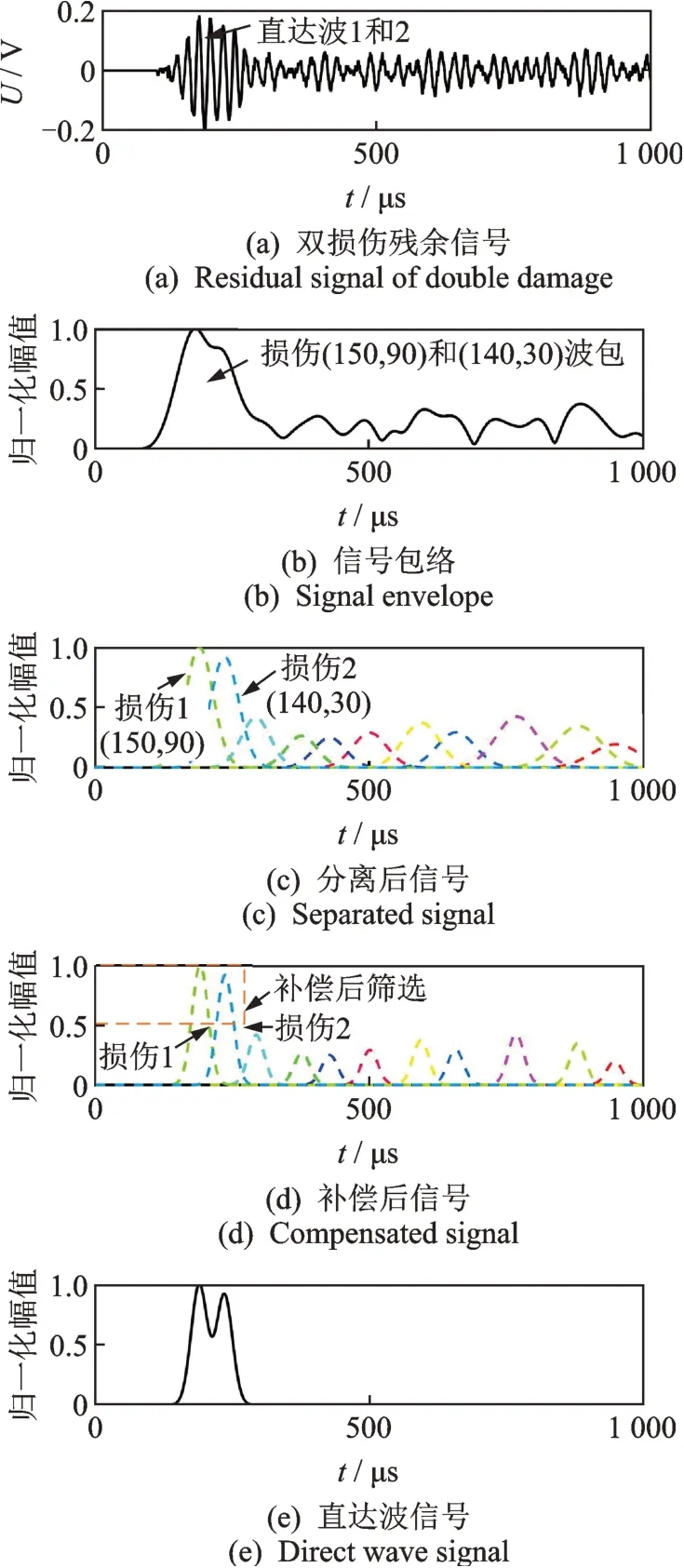
图9 双损伤传感器路径B-C间波包分离Fig.9 Wave packet separation of double damage on sensor BC path
对信号的包络Φ(t)进行波包分离(如图9(c)所示),时域上200和220μs的波包被分离出来,筛选直达波后映射到图10(b)中的定位图上识别出了2个损伤。在此基础上,对分离后的波包信号Φk进行频散补偿(如图9(d)所示),得到图9(e)中的直达波。因为波包分离和频散补偿的原因,使得时域上的200和220μs的波包重叠度变小,2个损伤对应的峰明显分离,映射到图10(c)的定位图上,计算得到改进后的DAS成像的SNR为3.16。而原始图像的SNR为2.68,双损伤定位的分辨率和精度得到了提高。
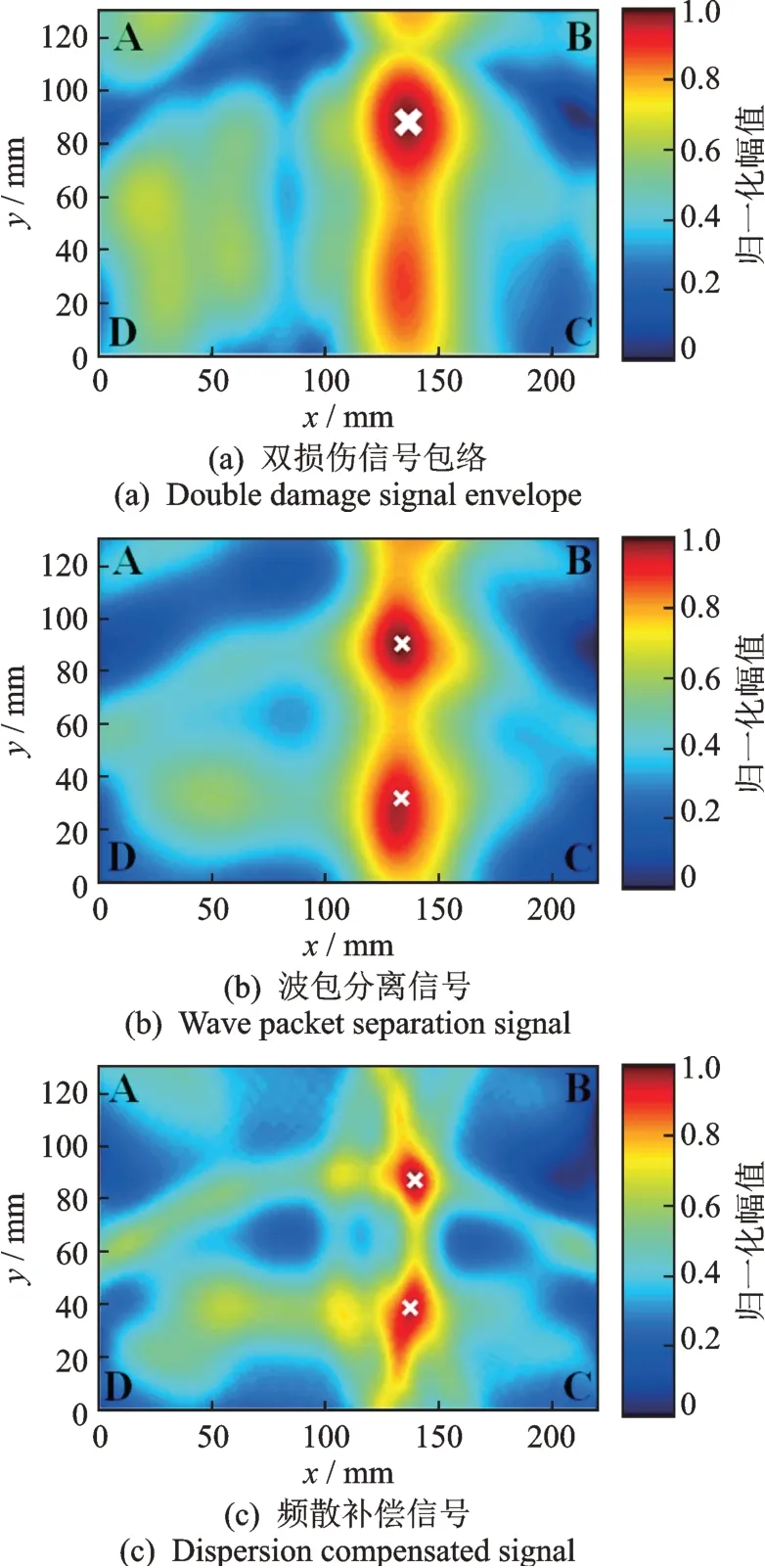
图10 双损伤信号定位结果Fig.10 Localization result of double damage signal
4 结束语
为了解决飞机结构中复杂边界条件对Lamb波产生反射而引起的损伤定位偏差,笔者提出了基于Lamb波波包混叠分离的损伤定位识别方法。根据Lamb波频散特性,建立了含有频散效应的Lamb波波包混叠模型,采用隐变量的概率估计方法实现了波包和函数的分离,并对重构出的波包和函数进行频散补偿和重组。以碳纤维复合材料板为例,通过数值仿真验证了波包分离方法的有效性。在飞机复合材料加筋壁板中进行了单损伤和多损伤的定位实验。结果表明,该方法可以分离直达波和反射波波包,并对各个直达波包进行频散补偿,结合自适应波包截取算法,实现了单损伤分辨率2.11~3.48,双损伤2.68~3.16的提升,相比于传统的延时累加定位方法具有更好的定位精度和抗混叠干扰的能力。
