基于差分式惯性传感组件的采煤机位姿解算法∗

司 垒，王忠宾，谭 超，梁 斌，2，万 淼

（1.中国矿业大学机电工程学院 徐州，221116）

（2.中国矿业大学徐海学院 徐州，221008）

关健词采煤机；位姿解算；惯性导航；精确定位

引言

煤炭是我国的主体能源和重要的工业原料。2019年，全国原煤产量38.5亿吨，同比增长4%［1］。近年来，受经济增速放缓、能源结构调整等因素影响，我国煤炭需求量有所下降。然而，我国富煤、贫油、少气的能源赋存特点，决定了煤炭将在一次性能源生产和消费中占据主导地位且长期不会改变。近年来，国家逐步加大煤炭智能化开采的力度，煤炭安全形势逐年好转。2019年，我国煤炭开采百万吨死亡人数0.083人，仍高于世界先进产煤国家。国家发改委、国家能源局联合发布的《能源技术革命创新行动计划（2016-2030）》中明确指出：提升煤炭开采效率和智能化水平，到2030年重点煤矿区基本实现工作面无人化。采煤机作为综采工作面的核心装备之一，其智能化是综采工作面能否实现无人化开采的关键技术，而准确定位是实现采煤机智能化的基础［2］。

由于煤矿井下的环境特殊、工况恶劣，地面常用的无线电导航、卫星定位等技术无法穿透地面对采煤机进行定位。现有的采煤机定位技术主要包括红外、超声波、齿轮计数、无线以及惯导定位技术等。国外学者对采煤机的定位研究较早，Jobes等［3］提出了一种采煤机的远程定位系统，并给出了计算位置和航向的方法。文献［4-5］通过轴编码器计算电动机的转速，进而换算出采煤机的前进距离。文献［6-7］利用超声波传感器测量煤壁返回的强回声从而感知采煤机的位置。在国内，随着红外技术的快速发展，刘清等［8］在采煤机上安装红外发射装置发射广角脉冲，通过液压支架上的红外接收装置接收信号，对接收信号的强弱进行分析，从而判断采煤机具体位置。张连昆等［9］将超声波发射装置安装在工作面巷道中，根据采煤机反射的超声波确定采煤机和巷道的相对位置关系。随着无线技术的日益成熟，文献［10-11］提出了移动无线传感网络来进行采煤机的定位，通过仿真研究无线测距误差、锚节点密度和锚节点基准坐标漂移方向等因素对采煤机定位精度的影响。

由于不依赖外界信息、也不向外辐射能量的优点，惯性导航技术逐渐成为自主导航的重要技术之一，国内外一些学者对基于惯性导航系统的采煤机定位技术进行了研究。澳大利亚联邦科学与工业研究组织推出了基于陀螺仪导向定位的自动化采煤方法（longwall automation steering committee，简 称LASC），LASC技术采用高精度光纤陀螺仪和定制的定位导航算法，解决了惯性导航系统与采煤机高度通信、采煤机起点校准、截割曲线生成和支架推移调整控制等难题。文献［12-18］分别对捷联惯导的偏差角校准算法、初始对准方法、姿态解算算法及其融合定位方法进行深入研究，在一定程度上提高了采煤机的位姿检测精度。

通过对国内外采煤机定位方法的调研和分析，国内外学者在该领域进行了大量且有意义的研究工作，但仍然存在以下问题：

1）传统的红外、无线、超声波及齿轮计数等采煤机常规定位方法，不能测量采煤机的航向，无法真正实现采煤机运动轨迹的监测；

2）采煤机惯性导航定位误差分析不全面，建立的位姿解算方法没有充分考虑采煤机的实际运动工况，影响实际应用的精度，难以满足采煤机的定位要求；

3）惯性导航系统容易随时间产生累积误差，减少惯性导航系统累积误差的方法主要集中在改进惯性导航算法和利用辅助定位手段方面，缺少从惯性系统结构上抑制累积误差的方法。

为了减少采煤机惯性导航定位的累积误差，提高采煤机的定位精度，笔者分析采煤机惯性导航定位产生的确定性漂移和非确定性漂移误差，研究基于差分式惯性传感组件的采煤机位姿差分解算方法，进而提高采煤机位姿解算精度，实现采煤机的准确定位和定姿。

1 差分式惯性传感组件融合模型建立

1.1 坐标系建立及转换过程

采煤机惯性导航定位利用惯性传感器固连在采煤机机身上，通过惯性传感器的陀螺仪和加速度计分别测量采煤机的角速度和加速度信息，导航计算机根据这些测量信息解算出采煤机在导航坐标系中的位姿信息。基本坐标系建立如图1所示。

图1 坐标系建立Fig.1 Coordinate system construction

在图1中：惯性坐标系用i表示，该坐标系是适用牛顿运动定律的参考坐标系；地球坐标系用e表示，固连在地球上，原点位于地球中心，也称为地心坐标系；导航坐标系用n表示，原点位于导航起始点处，文中设为采煤机运行的起始位置；x，y，z分别指向东、北、天方向，也叫东北天坐标系；计算导航坐标系用t表示，通过计算获得的导航坐标系，和真实的导航坐标系存在一定的误差，该坐标系的定义是为了进行采煤机惯性导航定位的误差分析；载体坐标系用b表示，固连在采煤机上，原点位于其重心。

采煤机的位姿信息是基于导航坐标系获取的，而采煤机的惯性导航系统感知采煤机的运动特性是在载体坐标系中，因此需要建立坐标系的变换矩阵。各坐标系可以通过绕3个方位轴旋转而得到：导航坐标系Oxnynzn绕z轴转动φ角度，获得坐标系Ox1y1z1；之后坐标系Ox1y1z1绕x1轴 转动θ角度，获得坐标系Ox2y2z2；最后坐标系Ox2y2z2绕y2轴转动γ角度，获得了载体坐标系Oxbybzb。为了方便获取采煤机的位姿信息，定义φ角为航向角，θ角为俯仰角，γ为横滚角。

1.2 差分布局方法

采煤机在进行惯性导航定位时，由于温度、震动等外界因素会导致安装在采煤机机身上的惯性传感器发生漂移误差。文中将惯性传感器发生的漂移误差归为两类：确定性漂移和非确定性漂移。确定性漂移指的是方向和大小确定的常值漂移，非确定性漂移指的是方向或大小不确定的随机漂移。为了消除确定性漂移误差和减少非确定性漂移，笔者设计一种基于差分式传感组件的误差消除方法，该方案主要采用4个惯性传感器构成差分布置，利用差分式惯性传感组件进行数据融合，通过位姿差分解算算法对融合后的数据进行位姿解算，得到采煤机准确的位姿参数。差分式惯性传感组件的布局方法如图2所示。

由图2可知，设计的差分式传感组件采用4个惯性单元构成差分结构，每相邻的两个惯性单元之间均有两个坐标轴反向。理论上，差分式惯性单元能够完全消除确定性漂移，降低非确定性漂移。

1.3 数据融合方程

1.3.1 角速度融合方程

图2 差分式惯性传感组件布局方法Fig.2 Differential inertial sensor module layout

当单个惯性单元发生绕某个轴转动时，其输出的角速度ω包括真实的角速度ωr、角速度确定性漂移ωc、角速度非确定性漂移ωu的矢量和

差分式惯性传感组件下的角速度可以表示为

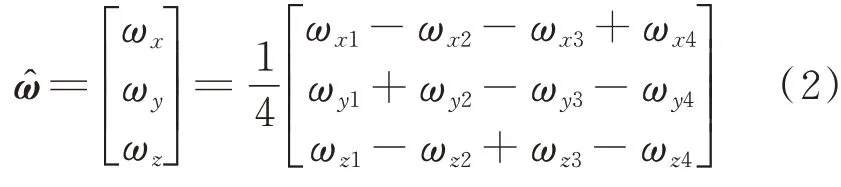
由于角速度确定性漂移ωc的大小和方向一致，因此在各个坐标轴方向可以相互抵消，而角速度非确定性漂移ωu由于大小和方向的不确定性不能相互抵消，根据式（1）和式（2）可获得角速度的数据融合方程

从式（3）可以分析出，确定性漂移可以通过差分方法完全消除，而非确定性漂移的相同部分可相互抵消，不同部分通过求其均值避免误差扩大。

1.3.2 比力加速度融合方程

当单个惯性传感器发生平动时，其输出的加比力速度f包括了真实比力加速度fr、比力加速度确定性漂移fc及比力加速度非确定性漂移fu

差分式惯性传感组件下的比力加速度可以表示为

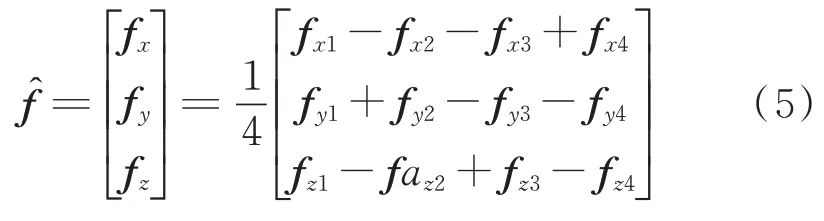
基于式（4）和式（5）获得比力加速度的数据融合方程

同样，分析式（6）可以得出融合后的比力加速度可以消除确定性漂移，降低非确定性漂移。

2 采煤机位姿差分解算算法

2.1 采煤机姿态差分解算算法

由于四元数法求解姿态矩阵实时性强，精度高，没有退化和奇点等现象，本研究采用四元数法求解采煤机的姿态变换矩阵，可以求得采煤机的姿态角

其中：q0，q1，q2，q3分别为四元数微分方程中的系数。

通过式（7）求得各姿态角的值域为-90°～90°，而通常定义的航向角范围为0°～360°，因此需要将航向角的值进行转换，得到航向角如下

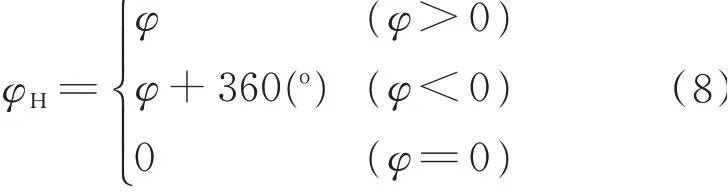
2.2 采煤机速度差分解算算法

在导航坐标系下，采煤机的速度更新方程可表示为

由于速度更新周期T较短，可以认为姿态变换矩阵Cnb对应的旋转矢量非常微小。因此对等式两边积分可以得到tk时刻在导航坐标系内的速度为

2.3 采煤机位置差分解算算法

为了方便计算，采煤机的位置方程可用其一阶近似表达式表示

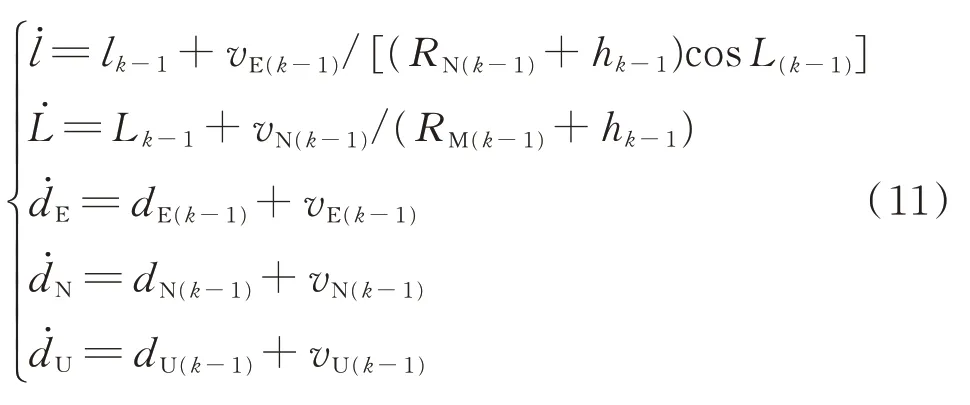
其中：l，L分别为当地经度和纬度；dE，dN，dU分别为采煤机在东、北、天三个方向上的位移变量；RM，RN分别为子午圈和卯酉圈曲率半径；h为地球曲率。

由于tk时刻的vn k已经求得，在位置更新过程中采用平均速度值，可以得到位置的表达式为

3 位姿差分解算算法仿真分析

3.1 采煤机运行工况分析

为了验证文中提出的采煤机位姿差分解算算法在不同运动工况下的位姿解算精度，需要获取不同运动工况下惯性单元的原始输出数据用于位姿差分解算算法的输入，并利用位姿差分解算法解算后的位姿信息和参考位姿信息进行对比。由于采煤机实际工作过程中环境比较复杂，条件有限，无法获取采煤机运行的实际参考运动数据。因此，笔者采用数值仿真法来模拟采煤机的不同运动工况。

采煤机的运动工况有直线运动、S弯运动、爬坡运动及起伏运动4种。其中直线运动和S弯运动在采煤过程中最为常见，爬坡运动是当底板产生了一定坡度时的采煤机运动工况，起伏运动是由于底板产生了起伏导致的运动工况。为了方便运动工况的模拟，需要定义一个采煤机运动轨迹坐标系m，x轴沿运动轨迹水平向右，y轴沿运动轨迹切线指向采煤机前进方向，z轴符合右手螺旋原则垂直于xOy面指向上，文中模拟运动工况时的加速度a（t）和角速度w（t）的定义均在此坐标系内。采煤机工作过程中，其基本的运动状态变化就是角速度w（t）以及加速度a（t）变化引起的。采煤机运动微分方程以采煤机运动工况分析中所述的角速度w（t）和加速度a（t）作为输入，直接积分求解便可获取各种运动参数。

3.2 仿真结果分析

利用文中提出的差分解算算法和原始解算算法获取的采煤机位姿信息，并与模拟出的采煤机参考位姿信息进行对比，得到位姿信息的误差曲线，以此验证提出的采煤机位姿差分解算算法的性能。由于在模拟起伏运动时，包含了直线运动、S弯运动和爬坡运动，因此限于篇幅，文中不单独进行直线运动、S弯运动和爬坡运动的模拟仿真。

起伏运动本质是俯仰角发生二次变化的运动，文中模拟的起伏运动包括凸起、凹坑和连续凸起凹坑3部分。起伏运动仿真中，采煤机初始姿态角α0=［0 0 0］，初始速度v0=［0 0 0］，初始位置p0=［0 0 0］，初始位移为d0=［0 0 0］，采煤机惯性导航输出频率（采样频率）fs=100 Hz。设置采煤机沿y轴方向（工作面前进方向）运动60 m，沿z轴方向（高度方向）运动最大为0.052 3 m。根据以上参数，结合采煤机运动工况模拟方法，通过计算便可获得起伏运动的仿真参数。图3为起伏运动3种轨迹对比。

图3 起伏运动的对比结果Fig.3 Comparative results of undulating motion

由图3可以直观看出，在起伏运动仿真中，差分解算算法能够更好跟踪基准轨迹，性能较好；而原始解算算法获得的运动轨迹偏差较大，在东向发生了明显的漂移，跟踪性能较差。

图4 为起伏运动模拟姿态角、速度、位移的解算误差对比结果，起伏运动是由于俯仰角多次变化导致，因此俯仰角的模拟曲线发生了多次突变。从图4（a）～（c）看出，原始解算算法在航向角最终累积误差为0.505 6°，俯仰角最终累积误差为-0.500 4°，横滚角最终累积误差为-0.484 6°；而差分解算算法在航向角最终累积误差为0.028 8°，俯仰角最终累积误差为0.014 6°，横滚角最终累积误差为-0.021 1°，差分解算算法明显具有更好的解算效果。从俯仰角的误差可以看出，笔者提出的差分解算算法具有较小的误差，说明在俯仰角突变的工况下，文中算法能够更好地抑制惯性传感器的漂移误差，从而减少了误差的累积。

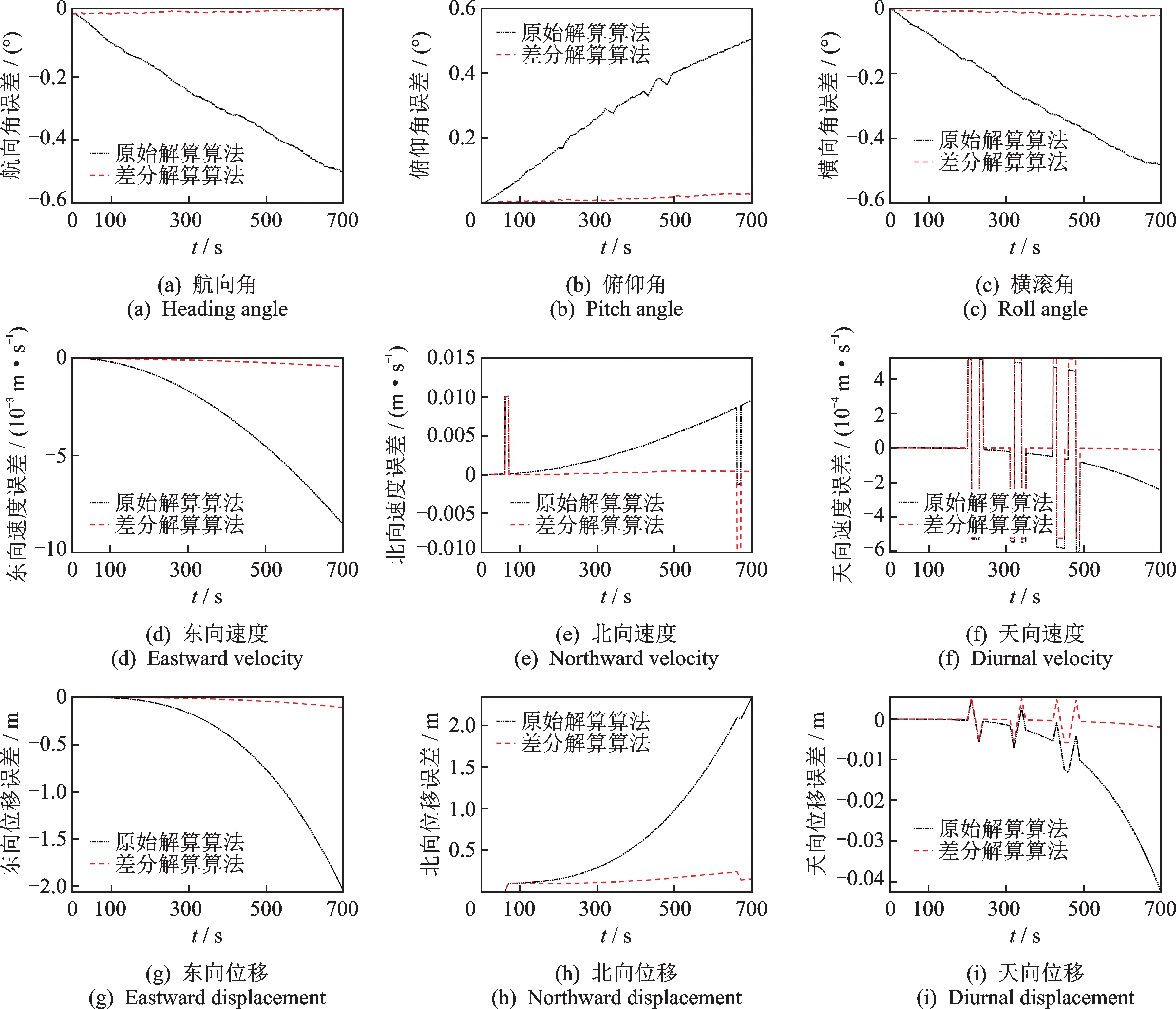
图4 起伏运动模拟姿态角、速度、位移解算误差对比Fig.4 The error comparison of undulating motion simulated attitude angle,velocity and displacement

从图4（d）～（f）看出，差分解算算法在东向速度上解算效果优势明显，同样，在北向速度和天向速度上，两个算法的最大误差方面几乎一致。同时，在天向由于俯仰角的多次变化产生了速度的突变，导致两种算法在天向上的跟踪性能相对较差，但是文中算法没有发生明显的漂移，在速度突变的工况下，具有更好的稳定性。

从图4（g）～（i）看出，原始解算算法在东向位移最终累积误差为-2.052 4 m，北向位移最终累积误差为2.347 5 m，天向位移最终累积误差为-0.042 3 m，而差分解算算法在东向位移最终累积误差为-0.107 2 m，北向位移最终累积误差为0.152 3 m，最大北向位移误差为0.237 2 m，小于原始算法的北向最大位移误差，天向位移最终累积误差为-0.002 0 m，最大天向位移误差为-0.005 7 m，明显小于原始解算算法的天向位移误差最大值。由上述仿真结果可以看出，笔者提出的采煤机位姿差分解算算法在不同工况下具有更高的解算精度。

4 实验验证

4.1 实验平台搭建

为了对采煤机位姿解算方法进行验证，文中搭建了采煤机惯性导航定位实验平台，并在矿山智能采掘装备省部共建协同创新中心进行地面实验，如图5所示。差分式惯性传感组件成差分布置固定在定位板上，定位板固联在采煤机机身上，差分式惯性传感组件和树莓派Raspberry Pi 3B通过杜邦线连接，树莓派Raspberry Pi 3B和上位机之间通过USB转TTL模块连接。

图5 实验平台Fig.5 Experimental platform

4.2 姿态定位实验

设置采煤机沿北向加速至3 m/min后减速至0 m/min后停止运行，运行时间总共为200 s。设定航向角、俯仰角和横滚角的初始对准角度分别为-0.792°，-0.064°和0.091°，以此作为动态定姿实验的初始值进行实验。为了验证文中所提方法的可靠性，采用高精度的惯性测量单元ADIS16448得到观测值进行对比，图6为动态定姿实验的采煤机航向角解算结果，文中所提方法在航向角的误差较大，最大误差为1.745°，平均误差为1.043°。同时，通过计算可以得出，文中所提方法在俯仰角和横滚角方面误差漂移均小于1°，整体漂移较小，具有较高的精度。

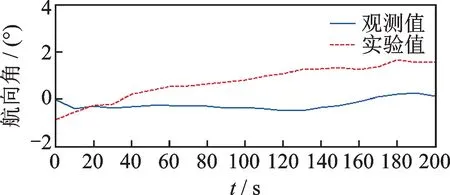
图6 采煤机航向角角解算结果Fig.6 Heading angle calculation of shearer

4.3 位置定位实验

考虑到实验条件的限制，设置采煤机沿北向往返运动，单程运行范围内同样先加速至3 m/min后减速运动，设置采煤机运行3次，单程位移为5 m，总位移为15 m。图7为动态定姿实验的采煤机东向位移解算结果。

图7 采煤机东向位移解算结果Fig.7 Eastward displacement calculation of shearer

由图7可知，随着时间的推移，文中提出的采煤机姿态解算方法东向位移跟踪上发生了一定的漂移，东向平均误差为0.157 m。同时，经过计算可以得到北向平均误差为0.409 m，天向平均误差为0.096 m。这是由于采煤机的位移需要经过对加速度两次积分才能获得，因此惯性传感器的漂移误差经过不断积分后被累积放大，特别是在东向和北向方面比较明显。

4.4 运动工况模拟实验

本研究根据实际情况，搭建了移动载体惯性导航定位实验台，进行S弯、爬坡、起伏3种运动工况的模拟实验，如图8所示。

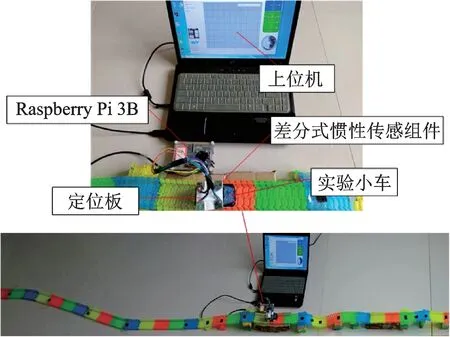
图8 运动工况模拟实验台Fig.8 Motion conditions simulation experiment platform

为了更好地模拟采煤机的S弯运动、爬坡运动和起伏运动3种运动，其模拟运动轨迹设置如图9所示，P0为起始点，P1～P4为模拟S弯阶段，设置沿y轴方向（工作面前进方向）运动0.9 m，沿x轴方向（工作面推进方向）运动0.1 m。P5～P8为爬坡阶段，爬坡高度设置0.04 m；起伏阶段为P9～P16，P9～P12设置为凹坑阶段，凹陷深度设置为0.01 m，P9～P16设置为凸起阶段，凸起高度设置为0.01 m；P17作为终点。在实验中，本研究可以准确获得各关键点的姿态信息和位置信息。

图9 模拟运动轨迹Fig.9 Simulated trajectory

为了进一步分析文中所提方法的有效性，根据以上节点的位姿数据拟合出真实的位姿曲线，并利用文中所提算法对姿态角和位置进行结算，对比结果如图10所示。

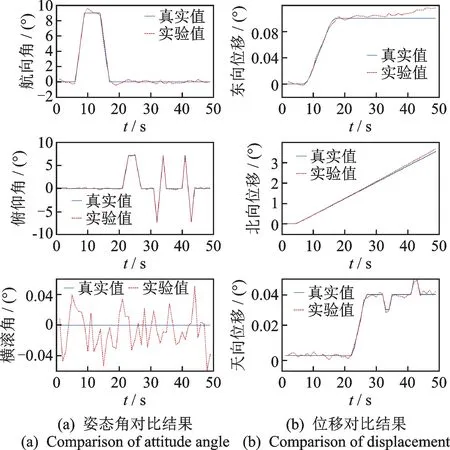
图10 姿态解算对比结果Fig.10 Comparison of attitude angle and position

由图10（a）可以分析得出，航向角的平均误差为0.183°，俯仰角的平均误差为0.123°，横滚角的平均误差为0.020°，三个方向的姿态角误差都控制在0.2°之内。由图10（b）可以分析得出，在东向和北向方面，文中方法获得的位移后期发生了一定范围内的漂移，而在天向的误差最小，这是符合运动规律的，因为在北向和东向运动距离较大导致产生一定漂移，而在天向运动距离小，因此漂移也较小。在东向平均误差为0.007 m，北向的平均误差为0.114 m，天向的平均误差为0.003 m。由此可见，文中提出方法在S弯运动、爬坡运动及起伏运动等工况下仍能保持具有较好的解算精度。

5 结论

1）为了减少采煤机惯性导航定位的累积误差，建立了采煤机差分式惯性传感组件数据融合模型，提出了一种采煤机位姿差分解算算法，并进行了不同运动工况下的仿真分析。仿真结果表明：在S弯运动、爬坡运动及起伏运动中，文中提出的差分位姿解算算法在累积误差和最大误差方面均小于原始位姿解算算法。

2）搭建了采煤机惯性导航定位实验平台，并进行采煤机直线运动实验，采煤机航向角、俯仰角和横滚角的平均误差分别为1.043°，0.251°，0.120°，其东向、北向和天向的平均误差分别为0.157，0.409及0.096 m，以上误差均满足采煤机定位精度要求，验证了采煤机位姿解算方法的可行性和有效性。

3）搭建了移动载体惯性导航定位实验台，并进行了S弯、爬坡、起伏3种运动工况的采煤机模拟运动实验。实验结果表明：在包含上述3种工况的路线运动时，移动载体的航向角、俯仰角、横滚角的平均误差分别为0.183°，0.123°，0.020°，东向、北向、天向位移的平均误差分别为0.007，0.114，0.003 m。实验结果验证了所提算法的适用性和可行性。