基于多速度调控的城轨列车区间运行策略优化
2021-04-28邓连波钟敏蔡莉
邓连波,钟敏,蔡莉
(中南大学,交通运输工程学院,湖南省轨道交通大数据实验室,长沙410075)
0 引言
城市轨道交通的列车运行能耗是运营成本的重要组成部分。本文针对限定运行时分条件下通过多速度参数调控城轨列车区间运行策略优化,力求有效降低城轨列车运行能耗。
当前研究主要集中在操纵模式和运行曲线、节能时刻表等方面。Asnis[1]等采用极大值原理证明最优速度曲线由“最大牵引、巡航、惰行、最大制动”这4种工况构成。Howlett[2]等提出局部能量最小化方法求解全局最优驾驶策略的关键转换点。一些学者通过调整影响列车能耗和性能的参数实现对列车驾驶策略的直接操控。Bocharnikov[3]探讨了运行能耗与区间运行时分的关系,以及加、减速度对列车节能的影响。Liu[4]等增加对列车控制的预测,通过调整线路最大速度和各区间的最低速度实现列车在满足运行时分下的节能控制。金炜东[5]等分析各子区间不同初始速度下改变各工况运行距离时运行能耗和运行时间之间的关系。刘炜[6]求解列车控制力系数优化序列解决地铁列车定时节能问题。一些学者从线路的节能设计和列车时刻表的节能优化讨论列车运行能耗问题。刘海东[7]等讨论曲线、坡道、站间距等对列车操纵策略和运行能耗的影响。Ning[8]等优化列车的区间运行时间、开行间隔、停站时间、牵引与制动的重叠时间来降低列车运行总能耗。Li[9]等定量分析牵引能耗、再生制动能和净能耗,建立综合模型,同时优化时刻表和列车速度曲线来降低净能耗。
本文提出基于多速度调控的城轨列车区间运行策略,考虑多种速度参数调控和区间运行时分取值要求下的城轨列车区间运行节能优化,根据区间内各线路段不同的限速特征,寻找包含区间的最高运行速度及最低惰行速度在内的最优速度控制参数组合,在满足运行时分取值约束的情况下使列车能耗最小。将列车运行速度参数作为优化变量,建立城市轨道交通列车区间运行策略优化模型与算法。在丰富不同区间运行时分下牵引曲线选择的同时,为列车运行图层面的再生能利用优化提供基础。在优化过程中,保持列车运行方案的操纵模式框架不变,通过速度参数调控实现区间运行方案的优化调整。
1 问题描述
列车区间运行策略优化问题是指考虑线路条件及列车所处位置的受力情况,列车从后方站速度为0 开始启动,运行至前方站指定位置停车,在运行过程中,改变列车不同位置下采取的运行工况,使得区间牵引能耗最小。对给定区间运行时分下的列车区间运行策略优化问题,还需要按照运行时分要求,按时到达前方车站指定位置停车。
城轨列车操纵模式一般分为巡航操纵模式(图1)和节能操纵模式(图2)。列车采用巡航操纵模式运行时,区间平均运行速度较高,可以实现较短区间运行时分。列车自后方车站发出,以最大牵引力加速至限速vˉ后,采取贴近限速的运行模式,当列车接近停靠站时,采用制动力使列车快速减速至0 并准确停靠在车站。在巡航操纵模式发车出站、进站停车运行模式不变的基础上,本文提出一种节能操纵模式,即地铁列车在区间中间段以牵引-惰行工况交替运行模式代替贴近限速的运行模式:列车加速至限速vˉ后,判断阻力产生的加速度是否可以使列车减速。若是,则转换为惰行工况并运行至速度接近最低限速-v(最低惰行速度),再转为牵引工况运行,当列车再次牵引加速至限速时,继续以该条件判断列车将要采取的运行模式;若否,如列车处在长大下坡道,则使列车贴近限速行驶。由此,将巡航操纵模式视作一种最低惰行速度等于最高运行速度的特殊情形的节能操纵模式。
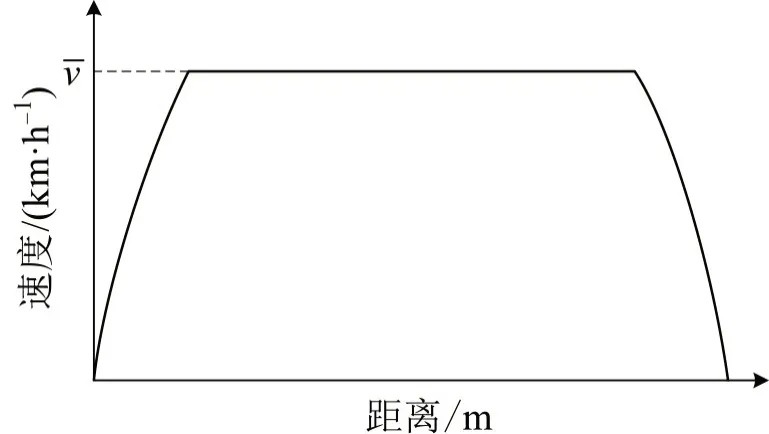
图1 巡航操纵模式Fig.1 Cruising operation mode
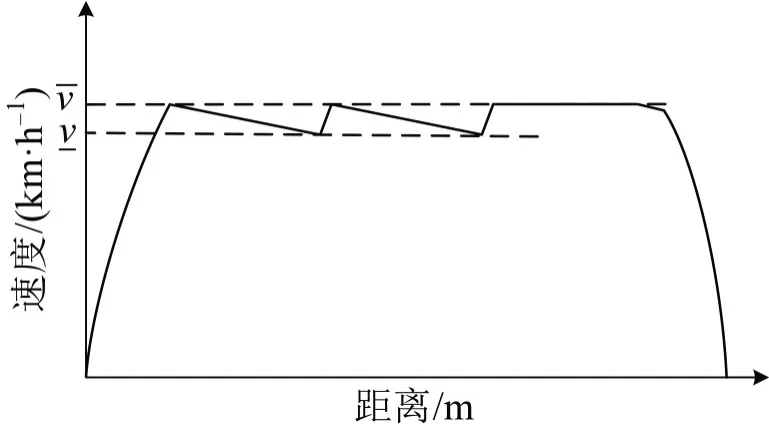
图2 节能操纵模式Fig.2 Energy-saving operation mode
2 优化模型
2.1 模型假设
以城轨列车在两相邻停靠车站间的区间运行过程为研究对象,在线路平纵断面、桥隧等运行环境和列车运行限速条件下,为实现特定区间运行时分要求,以列车运行能耗最小为目标,优化列车牵引运行曲线方案。为简化问题,进行如下假设:
假设1 对特定区间运行时分下列车运行方案的研究,采用均布质量模型[10]进行建模研究。
假设2 列车运行能耗只考虑列车在区间运行过程中的牵引等直接能耗,不考虑照明、空调、通风等辅助能耗。
假设3 列车总重量包含列车自重及载客重量,此处客流量采取某一满载率水平下所对应的客流载重量,从而将列车总重量视作一常数值。
假设4 只考虑单列车运行条件下的列车操纵模式和能耗,不考虑多列车条件下相互影响和作用关系,如同一供电分区内牵引、制动列车间的再生制动能利用等情形。
假设5 本文采用的最大牵引力、最大制动力均为综合考虑列车性能和乘客安全因素后列车可以获得的最大牵引力和最大制动力。
2.2 符号说明和变量定义
模型中的符号及说明如表1所示。

表1 模型的符号说明Table 1 Notations in model
2.3 目标函数
将最高运行速度、最低惰行速度占最高运行速度比例作为控制区间列车运行速度的两个参数,将这两个速度参数及相应的列车区间运行方案作为模型的决策变量,以区间内列车运行能耗最低作为优化目标函数。通过罚因子τ加权将运行时分的偏差考虑进目标函数,即

式中:为区间最高运行速度;μ为最低惰行速度占最高运行速度比率,为最低惰行速度,当μ=1.00 时,列车将采取巡航操纵模式运行;Send为区间终点位置;Et为运行时间t下的区间运行能耗;Δts为位置s对应上一个计算位置的时间增量。两参数的变动范围符合实际运营情况。
2.4 约束条件
(1)受力约束
牵引力Fs(v)与制动力Bs(v)的最大值由牵引、制动特性曲线通过线性插值方法计算得到,是关于列车速度的方程,即fF(v)和fB(v),列车实际所受牵引力及制动力取特性曲线对应的数值为

运行阻力W中基本阻力常以经验公式进行计算,附加阻力主要考虑坡道附加阻力、曲线附加阻力,即

式中:a、b、c为试验获得常数。因均布质量模型考虑列车长度,故列车的单位坡道附加阻力、单位曲线附加阻力计算需要考虑列车跨坡道、跨曲线的情形。根据线路及列车编组实际情况,列车最多同时横跨3 个不同坡度的坡道和3 个不同半径的曲线,即
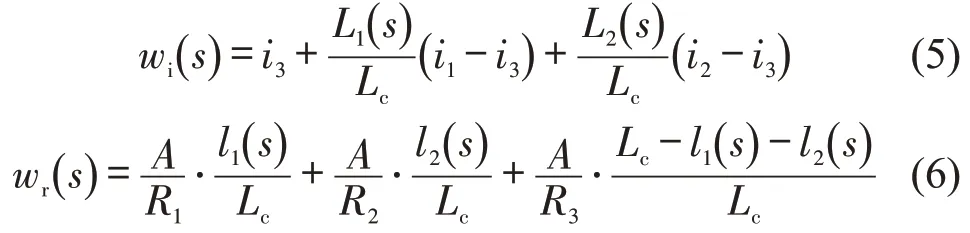
式中:i1、i2、i3分别为从车头至车尾列车横跨的坡道坡度;L1(s)、L2(s)分别为列车在位置s处在坡度为i1、i2的坡道上的列车长度;R1、R2、R3分别为从车头至车尾列车横跨的曲线段半径;l1(s)、l2(s)分别为列车在位置s处在半径为R1、R2的曲线上的列车长度;Lc为列车长度。在我国城市轨道交通中,A常取600。当列车位于1 个坡道上时,i2=i3=0,且L1(s)=Lc;当列车处于2 个坡道上时,i3=0,L1(s)+L2(s)=Lc。当列车位于1 个曲线段上时,l1(s)=Lc,l2(s)=0 ;当列车处于2 个曲线段上时,l1(s)+l2(s)=Lc。
(2)运动约束
列车运动方程满足
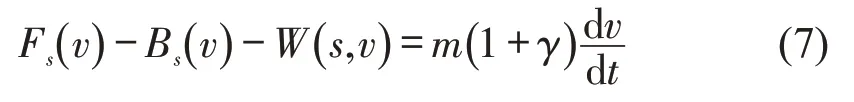
式中:γ为回转质量系数,通常取0.06。当列车处于牵引工况下,Bs(v)=0 ;处于巡航工况下,Fs(v)-Bs(v)-W(s,v)=0 且Fs(v)与Bs(v)不同时存在;处于惰行工况下,Fs(v)=Bs(v)=0;处于制动工况下,Fs(v)=0。
取足够小的位移Δs作为计算步长,并设定位移Δs内列车保持恒定加速度运行。根据动力学方程可知,列车运行速度、时间、距离之间满足
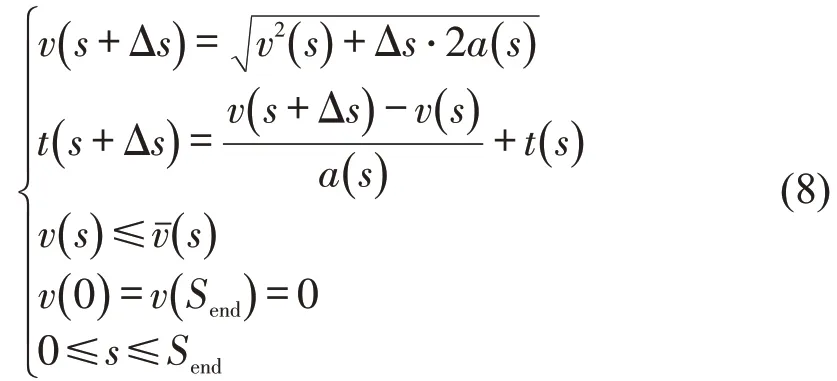
(3)制动工况转换点约束
为保证列车精准停靠在站时的速度为0 或者列车进入下一子区间时速度满足限速要求,采用从区间终点或者子区间终点反算迭代的方法求解制动工况曲线段,以此求得牵引(巡航或惰行)曲线段与制动曲线段的交点,即列车运动时从其他工况转为制动时的工况转换点的状态,应满足的位置及速度约束为
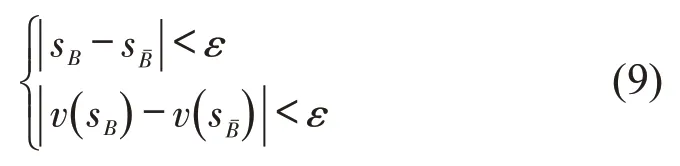
式中:(sB,v(sB))为制动工况下的位置速度计算点;(sBˉ,v(sBˉ))为非制动工况(牵引、巡航、惰行工况)下的位置速度计算点;ε为求解精度,与迭代步长Δs有关。满足上述约束条件的计算点(sB,v(sB)),即为列车由其他工况转为制动工况的转换点。
(4)区间运行时分约束
根据列车在区间运行时所含工况种类可知,列车在区间内不同工况下运行时间的总和应满足区间运行时分的要求,即

式中:t(,μ)为速度参数组合下的区间运行时分;ΔtF(s)、ΔtB(s)、ΔtW(s)分别为牵引(巡航)、制动、惰行工况下位置s对应的时间增量。
(5)区间运行能耗约束
根据列车牵引力做功的计算公式,列车在给定的控制方案(,μ)下,运行能耗为
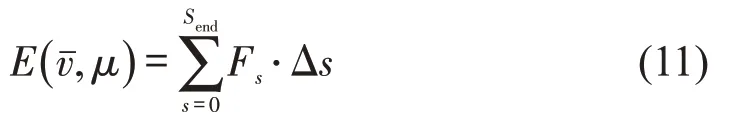
式中:Fs为位置s处的牵引力。
3 基于模拟退火的求解算法
列车区间运行策略的优化模型是一个大规模非凸优化问题,故釆用具有全局寻优能力的模拟退火算法求解。模拟退火算法的整体流程如图3所示,具体步骤如下。
Step 1 初始化。为提高搜索优解效率,在参数控制范围内,随机产生n个可行解,即控制方案(速度参数组合),计算对应的目标函数值N(x(0)),选择N(x(0))最小的可行解作为算法初始解,其对应的列车区间运行能耗值为E(x(0)),区间运行时分为t(x(0))。
Step 2 更新解。在当前温度,在取值范围内对参数进行扰动:计算单个参数改变单位值对区间运行时分的影响Δtj=t(x(j i)+dj)-t(x(i)),其中,dj为第j(j=1,2)个参数的单位值,x(ji)和x(i)分别为第i个解的第j个参数的数值和第i个解;计算当前解的区间运行时分与目标时间偏差Δt=t(x(i))-T,若Δt·Δtj <0(j=k或j=k′),则x(ji+1)=x(j i)+dj·βj,否则x(ji+1)=x(ji)-dj·βj。当dj >0 ,βj为区间上的随机整数,(xj)max为第j个参数的最大值;当dj <0 ,βj为区间上的随机整数,(xj)min为第j个参数的最小值。求得x(ji+1)(j=k)后,估算第k个参数改变后对区间运行时分的影响为βk·Δtk,则,进而求得x(ji+1)(j=k′)和x(i+1),以及新解的E(x(i+1))、t(x(i+1))和N(x(i+1))。记ΔN=N(x(i+1))-N(x(i))。
Step 3 Metropolis 准则判断新解是否被接受:若ΔN≤0,则接受x(i+1)作为新的当前解;否则,计算新解被接受的概率p=exp(-ΔN/α),随机产生[0,1)区间上的随机数r,若p >r,则仍接受x(i+1)为新的当前解,否则保留原来的解为当前解。
Step 4 若当前α下最优解连续200 次不变或达到内循环次数,判断是否达到算法终止条件。若无,则更新温度值,返回Step 2;否则,终止算法,输出结果。
4 实例分析
选取广州地铁8号线的中大-晓港区间为例,验证该优化模型和求解算法的有效性。区间长度为1.194 km,线路坡道及曲线数据如图4所示。运营列车采用4动2拖的A型车,其他参数如表2所示。
给定列车的取值范围为40~80 km·h-1,以1 km·h-1为单位;μ的取值为[0.70,1.00],以0.01 为单位。根据巡航操纵模式可以求得,列车在该区间运行的最短运行时分是69.39 s。以70 s 为最小目标区间运行时分,每隔5 s,求解区间运行优化控制方案。
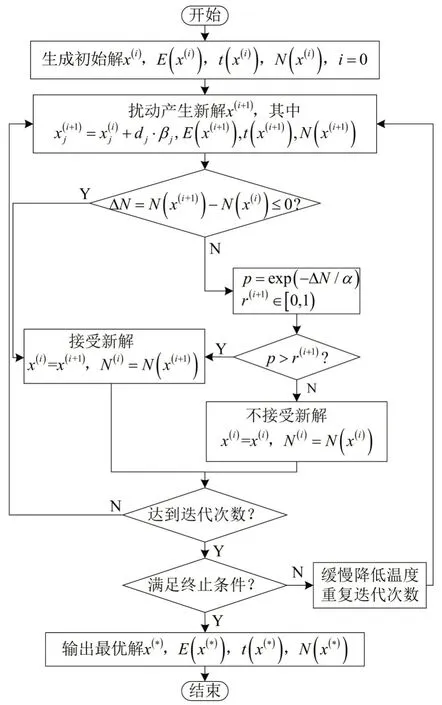
图3 模拟退火算法流程图Fig.3 Flowchart of simulated annealing algorithm

图4 区间线路坡道及曲线Fig.4 Gradient and curve data of section

表2 广州地铁8号线参数值Table 2 Parameters of Guangzhou metro line 8
模拟退火算法的终止温度为10-3℃,当算法执行到小于终止温度或最优解保持不变的迭代次数累积到300 代,算法终止。图5为目标区间运行时分为75 s时的列车运行能耗最优值的变化过程,在24代之后区间最优运行能耗趋于稳定。
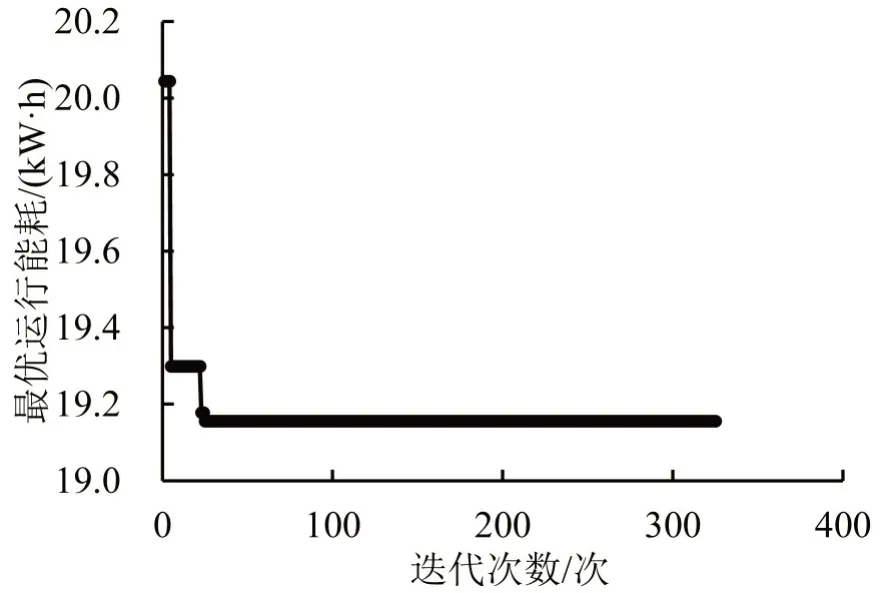
图5 75 s列车运行能耗最优值迭代过程Fig.5 Iteration of optimal train operation energy at 75 s
为分析同一区间运行时分标准下,巡航和节能两种操纵模式的能耗情况,引入根据最大值原理证明的“牵引-巡航-惰行-制动”四阶段操纵模式进行比较。以T=120 s 为例,不同操纵模式下列车的速度-距离曲线(V-S曲线)和时间-距离曲线(T-S曲线)如图6所示。列车采用巡航操纵模式运行的能耗为8.52 kW·h,40 km·h-1,如图6(a)所示;采用节能操纵模式运行时能耗为8.07 kW·h,40 km·h-1,μ=0.85,如图6(b)所示;在运行时间改变幅度较小时能耗节约5.30%;四阶段操纵模式下的最优运行控制方案如图6(c)所示,其惰行速度未作限制,该模式的最优能耗为8.05 kW·h,稍好于本文的节能操纵模式,但两种模式的能耗极为接近。

图6 120 s运行时分标准下不同操纵模式的V-S、T-S曲线Fig.6 V-S profiles and T-S profiles in different operation modes at 120 s running time standard
4.1 最优能耗与速度参数取值分析
两种操纵模式下的时间-最优运行能耗曲线如图7所示。结合表3,节能操纵模式下的最优能耗值低于巡航操纵模式。在相同时间标准下,节能操纵模式下的区间运行时分较长于巡航操纵模式,但能耗节约程度大,节能幅度在[0.16%,4.68%]。以95 s 为例,区间运行时分增加0.50%,能耗值节约2.34%,能耗节约量约为时间增加量的4.68倍,节能效果显著。
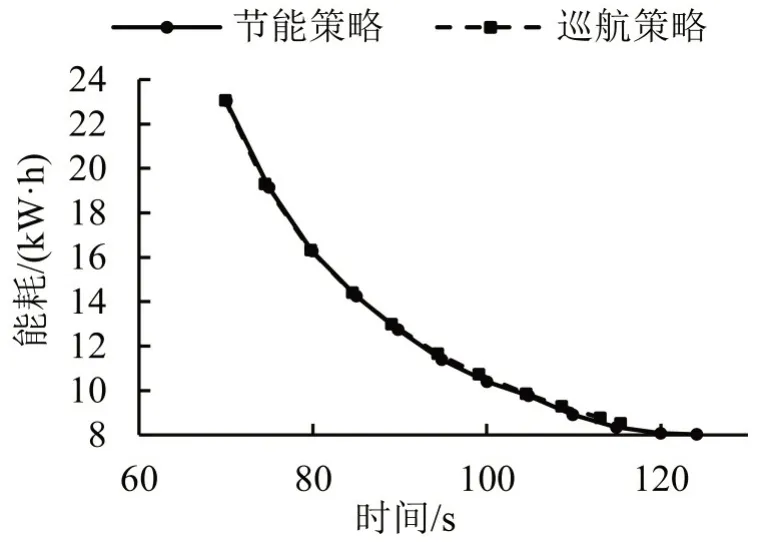
图7 不同区间运行时分下最优运行能耗曲线Fig.7 Optimal energy profiles at each running time
各区间运行时分标准下的最优运行控制方案的速度参数如图8所示。随区间运行时分增加,vˉ呈连续下降趋势;延长单位运行时间,vˉ降幅逐渐减小,其敏感度随区间运行时分增加而增大。μ总体呈下降趋势,在较短区间运行时分范围内,μ在较高水平上呈现缓慢波动下降趋势且下降幅度较小;区间运行时分较长时,μ迅速下降。μ在较长运行时分下的低速操纵模式中作用显著。
结合表3可知,在同一区间运行时分标准下,两种操纵模式下最优运行控制方案的vˉ基本相同,vˉ对运行时分取值范围起决定作用;在巡航操纵模式中引入μ,在几乎不改变区间运行时分的情况下能大幅度降低能耗。
4.2 不同区间运行时分下列车操纵模式选择分析
对于巡航和节能操纵模式的选择,依据表3中两者操纵模式下能耗情况,从节能角度分析,当运行时分T <85 s,两者的能耗差距极小;当运行时分T >85 s 时,节能操纵模式效果显著,最多可节约4.68%能耗。
进一步结合表3最优运行控制方案中速度参数取值情况,对操纵模式选择进行分析。当运行时分T <85 s 时,两种操纵模式能耗差距不大,且节能操纵模式μ取值接近1,故建议采用巡航操纵模式。当运行时分T >85 s 时,可以考虑采用惰行降低能耗:当85<T <100(T单位为s)时,单纯采用的调控(巡航操纵模式)即可实现运行时分调节,但采用节能操纵模式可对能耗状况有一定降低;当T >100 s 时,可以决定区间运行时分,调整μ可以有效降低能耗,节能操纵模式的优势较为明显。

表3 区间运行能耗优化前后对比Table 3 Comparison results of operation energy consumption
对于节能操纵模式中的μ,从图8(b)和表3可以看出,在70~80 s、80~95 s、95~110 s,110~115 s 几个时分段内其取值及惰行次数均呈现周期性波动,并在T >105 s 时保持在4~6次惰行的较低水平。由于过于频繁的牵引-惰行工况转换会增加列车操控复杂性,因而除节能幅度外,对惰行次数过大(如大于6)的运行时分,不建议采用节能操纵模式。
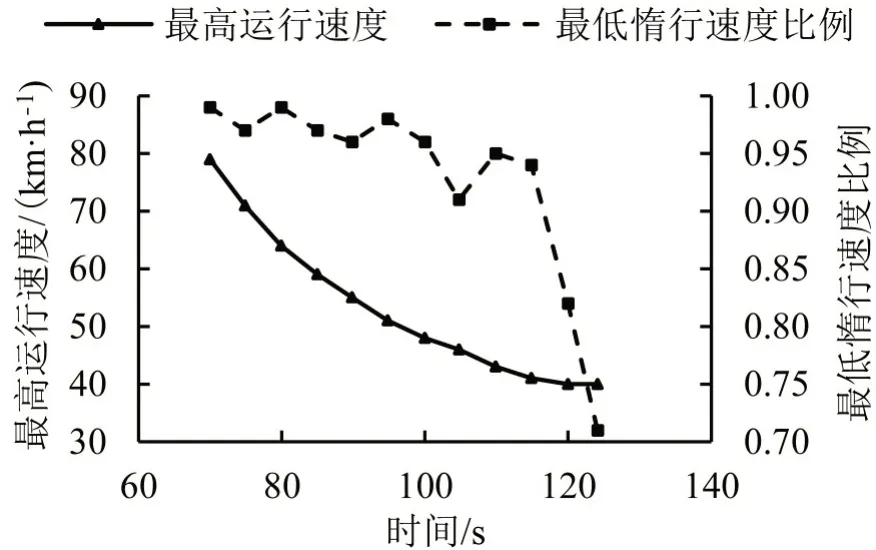
图8 最优运行控制方案的速度参数变化Fig.8 Speed parameters in optimal operation control scheme
5 结论
本文建立了基于多速度调控的城市轨道交通列车区间运行策略优化模型,优化确定了不同运行时分下最优列车区间运行控制方案集合,分析速度参数对区间运行控制方案、运行时分及运行能耗的影响,得出以下结论:
(1)最高运行速度与区间运行时分呈明显的减函数关系。对最优列车区间运行控制方案和区间运行时分、运行能耗具有决定性影响。因而,无论是线路技术标准确定还是车辆选型,均将vˉ作为重要技术参数。
(2)最低惰行速度在较长运行时分下的低速操纵模式中作用更为显著,给定区间最高运行速度情况下调节μ最多可节约能耗4.68%。在区间运行时分较长或非客流高峰期时,可调节μ降低能耗,其优化结果可为城轨节能化列车运行组织提供决策支持。
(3)列车操纵模式的确定需综合考虑运行时分取值、节能效果及惰行次数。对给定算例,当运行时分较短(小于85 s)时,建议采用巡航操纵模式;当运行时分较长(大于100 s)时,建议采用节能操纵模式;当运行时分介于两者之间时,需结合惰行次数确定应采取的操纵模式。
