施工区混行车流跟驰及换道模型研究

陈玲娟，张思琦，马东方

(1.武汉科技大学，汽车与交通工程学院，武汉430070；2.浙江大学，海洋学院，杭州310058)

0 引言

经济高速发展，车辆保有量日渐增多，交通拥堵及安全问题备受关注。尤其是城市建设形成的施工区较多，导致车道减少，驾驶环境复杂，车辆密集变道，交通拥堵时常发生。车联网技术通过车－车及车－路通讯，实现信息实时传递，车辆驾驶决策精细化，从而优化车辆通行效率、减少拥堵和事故。然而，实现高度自动化和全路网网联化仍需很长时间，普通车与网联车混行将长期存在，因此，本文以施工区交通流组织为研究环境，以混行车流为研究对象，分析驾驶特性、换道规则及车流分布规律。

国内外学者对跟驰模型和换道模型进行了不同程度的研究。跟驰模型包括：GIPPS 模型、IDM模型、Newell模型等。网联环境下考虑前后车通讯的跟驰模型也得到了更多发展。XIE等[1]分别采用最优速度模型和多重车头时距描述手动车辆和自适应巡航控制(Adaptive Cruise Control)车辆的运动规律。TALEBPOUR 等[2]采用IDM 模型模拟自动驾驶车辆及手动驾驶车辆间的决策交互。LI 等[3-4]采用修正的IDM 模型描述人类驾驶员、ACC 车辆和CACC(Cooperative Adaptive Cruise Control)车辆的跟驰行为。秦严严等[5]建立CACC 车辆跟驰模型，并分析不同CACC 比例下车辆的通行能力、通行安全及污染排放情况。换道模型方面，董长印[6]基于混行车流下匝道行驶特点，引入网联车感知区间、换道控制范围、换道冒险因子等参数，建立换道模型。胡远志[7]考虑换道意图和换道安全设计换道控制方法，通过模型模拟车辆轨迹。裴晓飞[8]基于深度强化学习算法TD3，构建换道模型并通过仿真验证TD3模型的有效性。

普通车的跟驰模型及换道模型已得到成熟发展，然而，对于网联车驾驶行为和运行规律仍处于探讨和摸索阶段。例如，不同车间距下的跟驰规律，换道点选择，区域换道意向，换道决策等问题在网联环境下均呈现独特性。因此，本文以施工区为研究环境，分析直行道跟驰模型及车道变少引起的混行车流强制换道决策机制，探讨不同网联车比例对施工区交通流组织及车流分布态势的影响。本文丰富了网联车驾驶行为理论，为新车型下施工区车流组织管理提供理论依据。

1 改进的混行车流元胞自动机模型

NAGEL 和SCHRECKENBERG 提出的一维元胞自动机NaSch 模型[9]将道路划分为若干个离散格，即元胞，同时将时域离散化为间隔为Δt的小段，元胞长度设为7.5 m，每辆车只占据1个元胞，每个元胞存在被占用或空置两个状态，相邻元胞可以同时被占用。每辆车速度离散化，可在0到最大速度Vmax间取整数值。但该模型不适用于网联车。网联车因车－车及车－路通讯，驾驶员能预知前方路况和前方网联车驾驶状态，规避碰撞的反应时间更短，故在驾驶决策和行为方面与普通车存在很大不同。因此，改进混行车流元胞自动机，增添规则如下。

(1)设元胞长度l=2.5 m，每辆车占用元胞数w=2。元胞自动机模型中时间间隔内加速为1个元胞长，根据车辆加速特性设定Δt=1 s。

(2)车辆占用2 个元胞，总长为5 m，减去车辆长度，前后相邻元胞内的前、后车辆间距符合网联车的安全间距，但不符合普通车的安全间距。因此，减速规则中设定普通车能往前行驶的间隔r比网联车少1 个元胞，即普通车前、后两车不能占据相邻元胞。其中，，Δs为两种车型的安全距离差值，可以根据不同车型对安全距离的要求调整元胞长度。

(3)随机慢化过程中，由于网联车可获知邻域内其他网联车辆的速度及位置，不确定性因素对车辆速度影响较小，故设定网联车随机慢化概率低于普通车。

改进的元胞自动机模型规则如下。

加速规则为

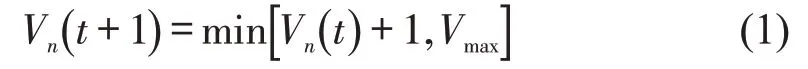
普通车减速规则为

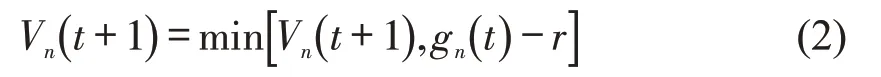
网联车减速规则为

随机慢化规则为网联车随机慢化概率为p1，普通车为p2，p1＜p2。

位置更新规则为

式中：Vn(t)、Xn(t)分别为t时刻车辆n的速度和位置；gn(t)为t时刻车辆n与前车的间距。

2 混行车流换道模型

2.1 网联车预期变道

仅考虑施工区车道封闭引起的强制换道，不考虑追求更高车速引起的自由换道。施工区域划分如图1所示。

图1为两车道路段，第2车道前方封闭。区域1在警告区外，在网联车通讯范围内；区域2 为警告区。普通车在区域2获知施工信息，寻求安全距离换道，而网联车在区域1即寻找合适时机进行预期变道。

图1 施工区域划分Fig.1 Construction area

车辆换道的约束条件为与目标车道前后车辆的间隔符合换道空间需求，施工区换道如图2所示。

图2 施工区换道示意Fig.2 Diagram of lane change in construction area

将2车道上换道车辆n映射到1车道的对应位置，记为车辆n′，计算车辆间隔。

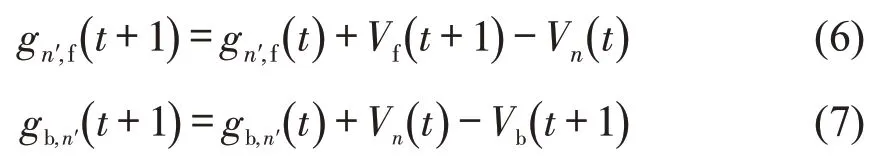
式中：gn′,f(t+1)、gb,n′(t+1)分别为t+1 时刻换道车辆n的映射位置车辆n′与目标车道相邻前车f 和后车b 的间距。计算映射间隔时选取车头占用的元胞进行映射，为防止碰撞需满足条件为

记sb(t+1)=λ·[Vf(t)-Vb(t)]+(1-λ)·Vmax，表示前车、后车跟驰行驶的安全舒适距离[6]。其中，Vf(t)、Vb(t)分别为前车、后车的速度，λ为权重参数，普通车和网联车取不同值。

在区域1，网联车的预期变道规则如下。

(1)若gn′,f(t+1)＞sn′(t+1)，且gb,n′(t+1)＞sb(t+1)，车辆n换道后能与相邻前车、后车保持舒适间距，此时换道概率P′=1。

(2)若gn′,f(t+1)＜0，或gb,n′(t+1)＜0，车辆n换道后与相邻前车或后车发生碰撞。若此时选择换道，且相邻后车为网联车，则需要通过换道前通信使相邻后车车速降低，给车辆n预留换道距离，此时随机换道概率较低，P′⊂(0 .0,0.5)，仿真时在取值区间随机生成概率。

(3)若0＜gn′,f(t+1)＜sn′(t+1)，或0＜gb,n′(t+1)＜sb(t+1)，可以完成换道，但换道后与相邻前车、后车需要进行速度调整才能达到舒适行驶间距，此时随机换道概率比规则(2)高，P′⊂(0.5,1.0)，仿真时在取值区间随机生成概率。

2.2 混行车流强制变道

记换道车辆n在时刻t到达区域2 的起点处，此时若满足舒适驾驶间距，直接换道；若不满足，执行如下规则。

(1)普通车通过近距离提醒本车道及目标车道前后车辆调整速度获得换道间距，普通车换道模型参考文献[10]。网联车根据通讯信息选择合适间隔进行换道，分为车距采集排序，换道执行及换道完成后跟驰3个步骤。

(2)车距采集和间隔排序。时刻t采集通讯范围内目标车道车辆位置，将换道车辆n之前的i辆车位置xf,i按距离由近及远加入集合Xf={xf,1,xf,2,…,xf,i} ，将车辆n之后的j辆车位置xb,j加入集合Xb={xb,1,xb,2,…,xb,j} ，分别对Xf、Xb计算车辆间距，得到集合Yf={yf,1,yf,2,…,yf,(i-1)}，Yb={yb,1,yb,2,…,yb,(j-1)}，其中，yf,(i-1)为车辆n之前的车辆间隔，为车辆n之后的车辆间隔，为避免车距采集间隔过远，车辆需要较长时间调整速度才能换道成功，使车辆拥堵且间距随时长变化较大，后方间隔选取靠近车辆n的5个间隔，即Yb={yb,1,yb,2,…,yb,5}；同时考虑前方间隔不得超出警告区，故前方间隔只采集在警告区末端范围内的至多5个间隔。

(3)换道间隔选择与换道执行。若选择集合Yb中间隔作为换道点，只需减速使车辆到达间隔区域；若选择Yf中间隔作为换道点，需考虑车辆n当前所在车道前方车辆的距离和速度约束，故选择换道间隔时，对集合的搜索顺序Yb优先于Yf，且距离车辆n更近的间隔优先搜索。

①若搜索到yb,k，使得yb,k ＞sn′(t+1)+sb(t+1)，车辆n选定间隔k，并且速度减少1 个单位直到时刻t′车辆n到达间隔k处，进行换道。

②若不满足规则①，但搜索到yb,k ＜sn′(t+1)+sb(t+1)，且间隔k后方为网联车m，则车辆n和网联车m通讯，并分别在本车道和目标车道速度减少1 个单位，直到时刻t′车辆n到达间隔k处，更新后的yb,k若满足yb,k ＞sn′(t′+1)+sb(t′+1)，即执行换道；若不满足，则t′+1 时刻重新采集车距和搜索间隔。

③若搜索到yf,k ＞sn′(t′+1)+sb(t′+1)，车辆n选定间隔k，并且速度增加1个单位，直到时刻t′车辆n到达间隔k处，即进行换道。

④若搜索到yf,k ＜sn′(t+1)+sb(t+1)，但间隔k后方为网联车m，车辆n选定间隔k，并且速度增加1 个单位，同时与网联车m通讯使其速度减少1个单位，直到时刻t′车辆n到达间隔k处，若满足安全间距，即换道；若不满足，则t′+1 时刻重新采集车距和搜索间隔。

⑤若集合内任意yb,k ＜sn′(t+1)+sb(t+1)，或yf,k ＜sn′(t+1)+sb(t+1)，且不存在间隔k后方为网联车的情形，车辆n速度减少1 个单位，并在t+1 时刻重新采集车距和搜索间隔。

(4)换道完成后跟驰。车辆完成换道后按照改进的NaSch模型跟驰行驶。

3 仿真实验及结果分析

3.1 实验基础数据

以图1路段为例，每个车道定义元胞数q=3000 个，总长为7500 m，车辆数z=200。设置仿真时长T=1000 s，仿真间隔Δt=1 s，车辆最大速度为30 m·s-1，对应元胞Vmax=12。图1中各段长度转化为元胞数量，E=390(区域1)，S=210(区域2)，上游过渡区Ls=18，缓冲区H=21，工作区G=390。舒适安全距离参数λ，网联车取0.6，普通车取0。为使研究不失一般性，车辆属性在既定比例下随机确定。初始车流，即t=1 s 时的车辆位置Xn(1)，即车道Mn(1)及初始速度Vn(1)为

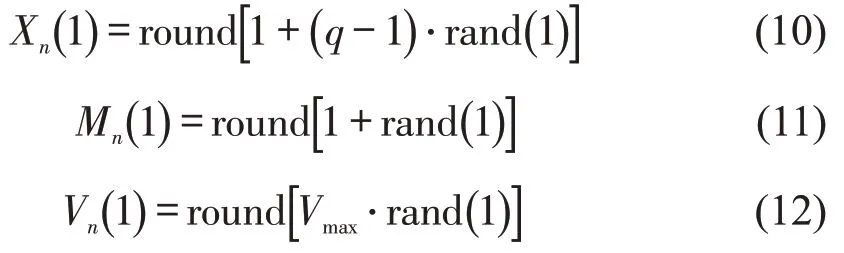
式中：round 为四舍五入取整函数；rand()1 函数产生一个在(0,1)之间均匀分布的随机数。式(10)～式(12)的初始车流产生规则中，为保持路段中车辆比例不变，在路段起点没有车的情况下，将驶出车辆循环放入路段起点，并将车辆速度重新初始化。

3.2 MATLAB仿真流程

采用MATLAB编码仿真混行车流的跟驰及换道算法，仿真流程伪代码如表1所示。

3.3 结果分析

分别设置网联车比例ρ为0.0，0.3，0.5 和0.8，施工路段通过车辆数为仿真时间内通过施工区横断面的车辆总数，时刻t车辆平均速度为

式中：c(t)为t时刻通过的车辆总数。

分析施工路段的通过车辆数、车辆平均速度、车辆换道点分布及车辆轨迹，结果如图3～图9所示。

随机设定车辆初始分布的位置、速度及车辆走行过程中随机慢化概率等参数，每个比例下各进行30次仿真。由图3可知：同一比例下多次仿真得到的通过车辆数虽有不同但波动不大，网联车占比较低时，路段通过车辆数较少，验证了提高网联车占比可以提高施工区通过能力。由图4可知：由于初始车辆密度的设置，运行初期路段发生拥堵，导致车辆平均速度降低，运行一段时间后车辆稳定行驶；网联车占比越高，路段平均速度越高。

由图5可知，网联车比例越高，网联车在预期换道区的换道点越靠近强制换道区。由图6可知，网联车在强制换道区的换道点大多位于强制换道区的前半部，比例越高，换道点越靠前。由图7可知，由于强制换道区长度的限制，普通车换道必须在强制区完成，故网联车比例对换道点分布影响不大。

表1 混行车流运行规律仿真流程Table 1 Simulation of mixed traffic flow

图3 不同比例下通过车辆数Fig.3 Total number of passing-through vehicles

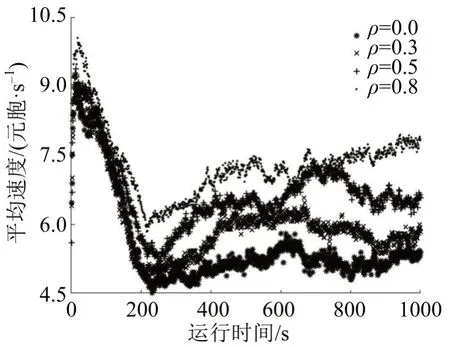
图4 不同比例下车辆平均速度Fig.4 Average speed for different proportions

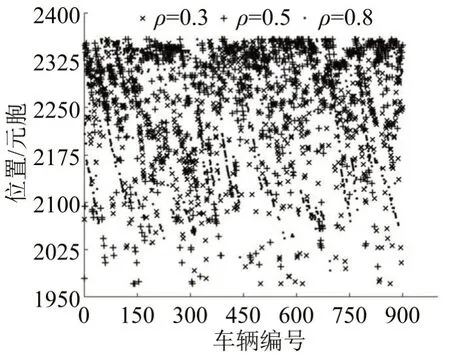
图5 不同比例下网联车预期换道点Fig.5 Distribution of excepted lane-change points

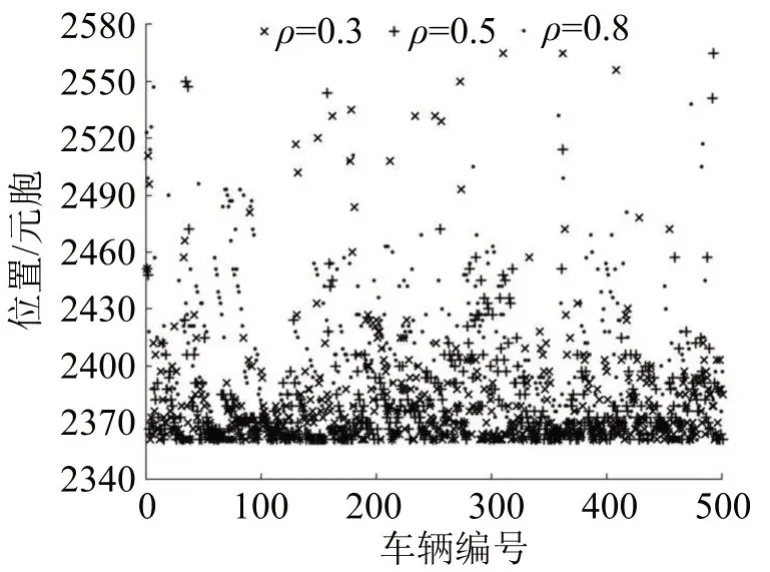
图6 不同比例下网联车强制换道点Fig.6 Distribution of forced lane-change points

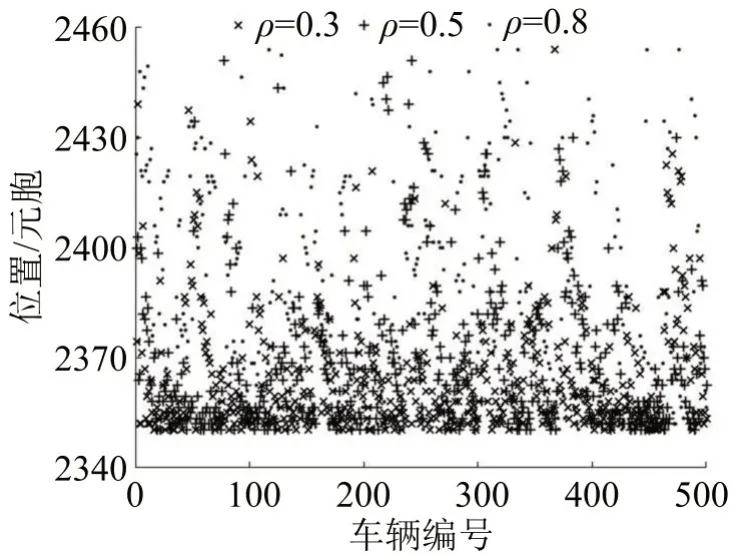
图7 不同比例下普通车强制换道点Fig.7 Distribution of forced lane-change points for human-driven vehicles

图8和图9为不同混行比例车流下，随机选取的多条完整轨迹。可知：车辆通过施工路段时产生不同程度的拥堵，在元胞位置2100～2400 时，该区段通行时间变长，速度大幅降低。由于普通车无预期变道只能强制换道，因此，对车辆正常行驶影响较大，在相同比例时普通车通过拥堵路段比网联车所需时间更多。随着网联车比例增加，普通车和网联车通过拥堵路段的时间均减少，网联车减少更明显。

图8 不同比例下普通车轨迹Fig.8 Human-driven vehicles'trajectory

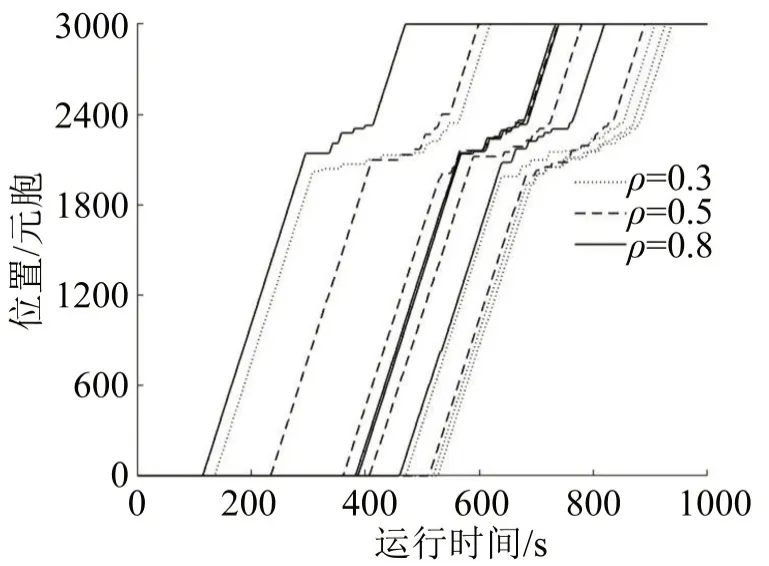
图9 不同比例下网联车轨迹Fig.9 Connected vehicles'trajectory

4 结论

由施工区车流轨迹可知，所有车辆通行保证了安全驾驶间距，网联车小于普通车的间距需求，仿真模拟的跟驰和换道过程中没有出现车辆碰撞等现象，验证了改进的NaSch元胞自动机模型兼顾了两种车型的安全间距需求，同时，可以离散化模拟车流运行规律。基于前后空位搜索和间距排序的换道规则保证了换道成功率及双车道车流的平稳性。因此，所建模型能有效用于施工区车流运行状态模拟。通过对案例所在路段车流的仿真实验，得出的换道点分布及车辆运行轨迹的相关结果，有助于为施工区设计最佳警告区长度和引导措施等。