城市立交匝道桥箱梁结构形式设计比选

2021-04-28王思伟

湖南交通科技 2021年1期

肖伟，王思伟

(湖南中大设计院有限公司，湖南长沙 410075)

0 引言

小半径曲线梁桥因结构性强、施工操作性好及外观优美等优点，近年来逐渐在我国城市桥梁建设中得到广泛应用[1-2]。但在早期竣工的曲线桥工程中，出现过由支座脱空引起的桥面侧翻及倒塌等重大事故，严重影响了桥梁的安全使用，针对该类型桥梁的设计进行深入研究具有重要意义[3]。

国内外学者关于曲线梁桥的结构设计展开了大量研究，如蒋超[4]针对城市大型立交连续箱梁桥的设计工作进行分析，并且根据不同方面的影响因素提出了有效的施工核心技术。何雄君等[5]利用Midas建立武汉市某立交匝道桥有限元模型并进行分析计算，证明了曲线半径的取值、车辆荷载的交通管控及曲线桥的支座布置形式等均对大跨度小半径曲线梁桥的抗倾覆稳定有较大影响。史方华等[6]提出一种新型弯桥支座布置方案及支座形式，通过建模分析证明了此布置方案可用于实现箱梁倾覆变形的分类控制，为曲线梁桥提升抗爬移及提升倾覆承载力提供科学经济的解决方案。辛法[7]依托长治至临汾高速公路项目中一处实体工程进行了独柱墩曲线梁桥支承情况分析，发现采用端横梁加宽拉大边支点间距、中支点向曲线外侧预偏的工程措施可明显改善结构受力。上述研究在比较曲线桥梁结构参数时，大多是针对同类型箱梁结构进行参数设计，而关于不同箱梁结构形式的设计研究还有待进一步完善。基于此，本文针对某城市立交匝道桥原设计方案，提出了一种更具优势的箱梁结构形式，并对比分析了两种箱梁结构桥梁的变形机理及受力特点，其结论可为类似小半径曲线梁桥的设计研究提供一定参考。

1 工程概括

某城市立交匝道桥平面线形位于R=60 m的圆曲线上，纵坡3.2%，上部结构采用钢 — 混凝土叠合箱梁，截面形式为单箱双室连续箱梁，跨径布置为20 m+2×30 m+20 m，填筑采用C50混凝土，箱梁顶板宽9.25 m，底板宽5.8 m，跨中和支点梁高均为2.0 m，梁端横梁宽为1.5 m，中跨横梁宽2.0 m，跨中位置布置一道宽40 cm的横隔板，每个腹板布置4根预应力钢束，采用φ15.2低松弛高强度钢绞线。桥面设计宽度8.75 m，单向两车道，最高时速40 km/h，荷载等级为公路-Ⅰ级。下部结构桥墩采用双薄壁空心墩，填筑采用C40混凝土，每墩布置3道横系梁，桩基础采用钻孔灌注桩，直径为50 cm，呈梅花形布置。上、下部结构连接支座采用盆式橡胶支座，间距4.5 m。桥梁立面布置如图1所示。

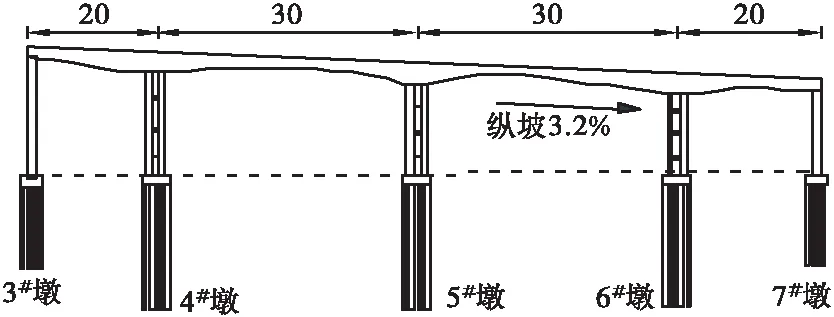
图1 桥梁设计立面布置图(单位： m)

2 箱梁结构形式设计及建立模型

为选择更为理想的箱梁结构形式，提高曲线梁桥的安全稳定性，采用预应力混凝土单箱单室箱梁形式与原桥设计的箱梁结构形式进行曲线梁桥受力对比分析。通过运用有限元软件MIDAS/CIVIL建立原钢 — 混凝土连续曲线梁桥数值模型，其中上部结构主梁及下部结构桥墩和桩基均采用梁单元模拟，计算模型中共包含682个单元和733个节点。全桥有限元模型如图2所示。

图2 桥梁有限元模型示意图

建模时保持其他设计参数不变，仅改变箱梁结构形式，以确保计算结果的精准性。计算过程中采用恢复力模型来模拟活动支座，对固定支座进行现行约束处理，对桩基进行非线性弹簧约束处理，墩梁连接采用固结形式。计算参数：C50混凝土容重取26 kN/m3，弹性模量取3.5×104MPa，泊松比取0.25；C40混凝土容重取24 kN/m3，弹性模量取3.25×104MPa,泊松比取0.25；φ15.2钢绞线容重取78 kN/m3，弹性模量取19.5×104MPa，泊松比取0.3。计算荷载主要考虑恒载+活载作用，设计汽车荷载为城市-A级，人群荷载为7.8 kN/m2。

3 成桥阶段受力对比分析

运用软件分别建立预应力混凝土连续箱梁和钢 — 混凝土叠合箱梁曲线梁桥计算模型，并针对桥梁两种结构形式成桥阶段的竖向挠度、支座反力、结构扭矩及剪力变化规律进行对比分析。

3.1 挠度对比分析

分别计算2种箱梁结构形式曲线梁桥的主梁中跨各关键截面挠度值，并针对其最大竖向挠度值进行对比分析，计算结果如图3所示。

图3 2种结构形式最大挠度变化曲线

根据图3可知，不同箱梁结构形式的曲线梁桥主梁各截面最大竖向挠度变化趋势存在较大差异，其中采用预应力混凝土箱梁的桥梁各截面竖向挠度整体变化相对较小，而采用钢 — 混箱梁的桥梁各截面竖向挠度变化相对较大。采用预应力混凝土箱梁和钢 — 混箱梁的曲线梁桥跨中截面的竖向挠度相差较小，最大值分别为-5.26 mm和-7.78 mm，相差仅-2.52 mm，而2种箱梁形式桥梁边跨截面的竖向挠度值相差较大，其中采用预应力混凝土箱梁的桥梁边跨截面最大竖向挠度分别为-6.76 mm和-6.34 mm，采用钢 — 混箱梁的桥梁边跨截面最大竖向挠度分别为-39.26 mm和-39.47 mm，二者差值达到了-32.5 mm和-33.13 mm，相对于跨中截面的最大竖向挠度差值更大，由此说明2种箱梁形式对于曲线梁桥跨中挠度的影响基本一致，但钢 — 混箱梁对于桥梁边跨挠度的影响要远远大于预应力混凝土箱梁结构。

3.2 支座反力对比分析

分别计算2种箱梁结构形式曲线梁桥3#～4#墩的支座反力值，并针桥梁曲线内、外侧最大支座反力进行对比分析，计算结果如图4所示。

图4 2种结构形式支座反力变化曲线

根据图4可知，不同箱梁形式的曲线梁桥各墩支座反力基本呈对称分布，且边墩内外侧的支座反力均小于中墩内外侧的支座反力。预应力混凝土箱梁结构桥梁的各墩曲线外侧支座反力均要小于内侧支座反力，采用钢 — 混箱梁结构桥梁的各墩曲线外侧支座反力均要大于内侧支座反力，2种箱梁结构的桥墩支座反力大小分布正好相反。采用钢 — 混箱梁的桥梁边、中墩最小支座反力分别为446 kN和1 441 kN，而采用预应力混凝土箱梁的桥梁边、中墩最小支座反力分别为749 kN和2 459 kN，相对于钢 — 混结构桥梁支座反力储备更为充足。其中预应力混凝土结构和钢 — 混结构桥梁的边墩内、外侧支座反力最大差值分别为1 505 kN和351 kN，中墩内、外侧最大差值分别为2 097 kN和3 222 kN，考虑到中墩作为曲线梁桥的主要承重结构，其曲线内、外支座反力差值过大极易出现偏载现象，严重时会导致桥梁发生倾覆。综合支座反力储备情况和桥梁稳定性来看，该曲线梁桥箱梁选择预应力混凝土结构更有优势。

3.3 扭矩对比分析

分别计算2种箱梁结构形式曲线梁桥3#～4#墩的扭矩值，并针桥梁边墩及中墩的最大扭矩值进行对比分析，计算结果如图5所示。

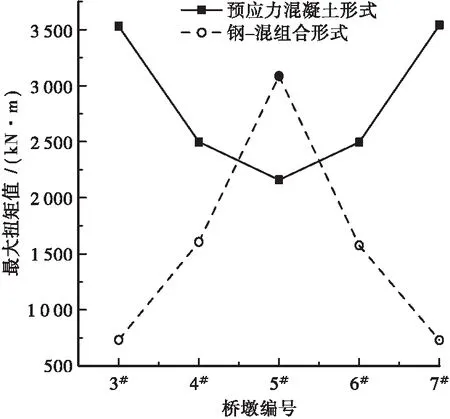
图5 2种结构形式最大扭矩变化曲线

根据图5可知，2种箱梁结构桥梁各墩的最大扭矩值分布形式存在较大差异，其中预应力混凝土箱梁结构桥梁边墩的最大扭矩值要大于中墩最大扭矩值，边、中墩最大扭矩值分别为3 529 kN·m和2 159 kN·m，整体相差约38.8%，而钢-混箱梁结构桥梁的边墩扭矩值要远小于中墩，边、中墩最大扭矩值分别为730 kN·m和3 085 kN·m，整体相差达到76.3%。钢-混箱梁结构桥梁的边、中墩最大扭矩差值相对较大，约为预应力混凝土箱梁结构边、中墩扭矩最大差值的1.9倍，曲线梁桥边、墩最大扭矩差值过大不利于扭力在全桥范围的合理分布，因此，该桥选择预应力混凝土箱梁结构形式可以使曲线梁桥结构受力更为合理。

3.4 结构剪力对比分析

分别计算2种箱梁结构形式曲线梁桥3#～4#墩的剪力值，并针桥梁边墩及中墩的最大剪力值进行对比分析，计算结果如图6所示。

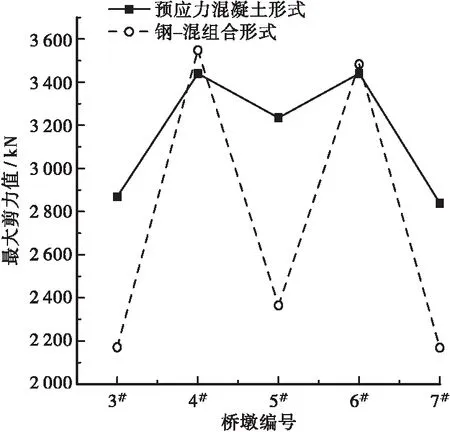
图6 2种结构形式最大剪力变化曲线

根据图6可知，采用不同箱梁结构桥梁各墩所产生的剪力值应力不同，其中曲线桥4#和6#墩的最大剪力值相差不大，但3#、5#及7#墩的最大剪力值相差较为明显，说明箱梁结构形式对桥梁剪力值存在较大影响。2种箱梁结构桥梁边墩的最大剪力值均要小于中墩的最大剪应力，其中预应力混凝土箱梁结构桥梁边、中墩最大剪力值分别为2 839 kN和3 440 kN，整体相差约17.4%，而钢 — 混箱梁结构桥梁的边、中墩最大剪力值分别为2 169 kN和3 548 kN，整体相差达到38.7%，相对于预应力混凝土箱梁结构桥梁的边、中墩最大剪力差值更大，相差约2.2倍。由此可知，该桥选择预应力混凝土箱梁结构可以使曲线梁桥剪力分布更为均匀，结构受力更为合理，相对于钢 — 混箱梁结构更具优势。