考虑断面形变的贴片式滴灌带局部水头损失研究

2021-04-28王亚林鞠学良胡紫寒赵永宏

干旱地区农业研究 2021年2期

王亚林，鞠学良，李萌，胡紫寒，赵永宏

(1.三峡大学水利与环境学院，湖北宜昌 443000; 2.国家电网陕西省电力科学研究院国家电网公司环境保护重点实验室,陕西西安 710054; 3.三峡大学生物与制药学院，湖北宜昌 443000)

滴灌作为高效的节水灌溉方式在许多干旱缺水地区广泛应用。在滴灌设计时，灌水均匀性是滴灌设计的重要指标，而准确计算毛管水头损失是评价灌溉均匀性的基础。毛管水头损失包括管段沿程水头损失和滴头段局部水头损失。对于毛管沿程水头损失，主要依据Darcy-Weisbach公式计算[1]，其公式如下：

(1)

式中,hf为毛管沿程水头损失(m)；λ为沿程阻力系数；d为毛管内径(m)；l为毛管长度(m)；v为毛管水流流速(m·s-1)；g为重力加速度(m·s-2)。

在Re(毛管水流雷诺数)<2000的层流范围内，沿程阻力系数主要采用Hagen公式：

(2)

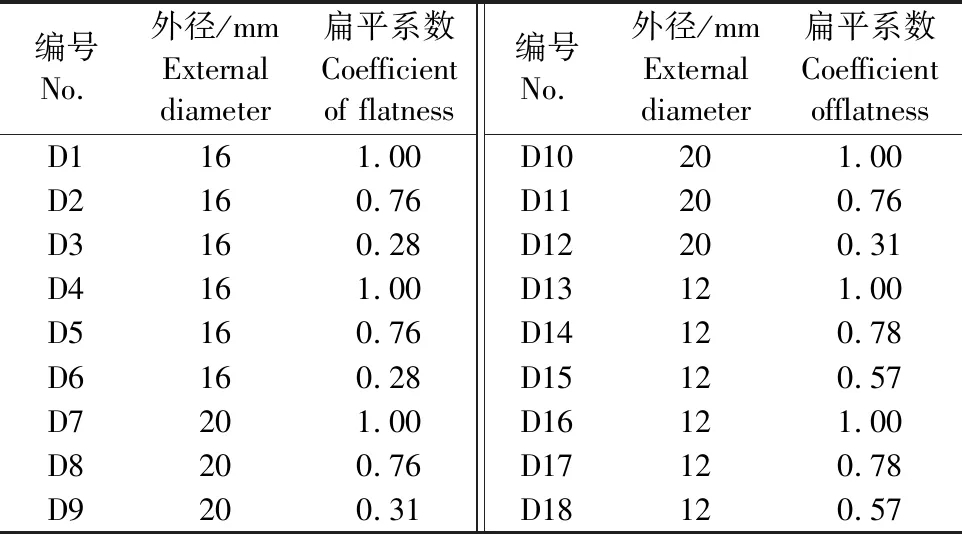
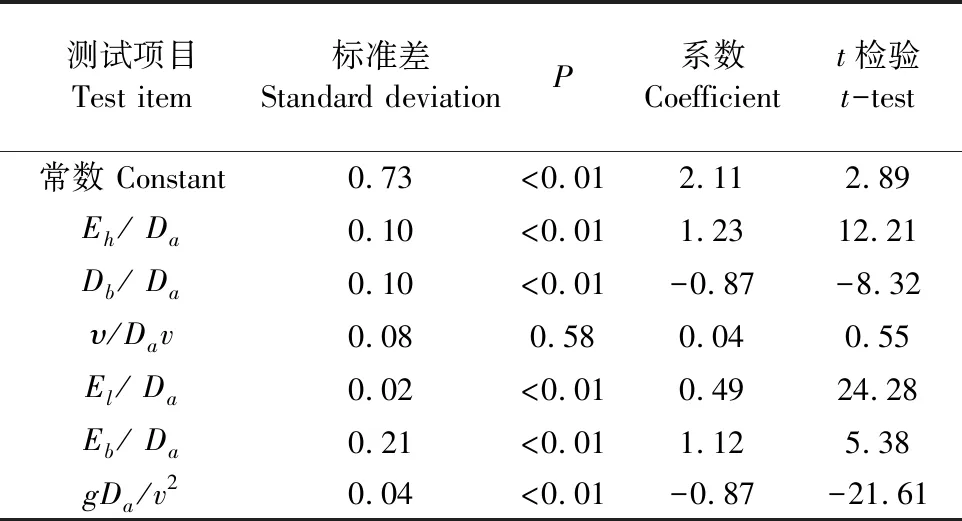
在3000

(3)

滴头局部水头损失由式(4)和式(5)求得。

(4)

(5)

式中,Δh为毛管总水头损失(m)；hj为滴头局部水头损失(m)；n为滴头个数。

局部水头损失因滴头形状复杂多样仍存在很多问题，毛管局部水头损失计算并未出现被普遍认可的理论公式。低压滴灌因其高效节能的特点在微灌领域得到广泛应用。滴灌带壁较薄且常工作于低压环境下，而低压下滴灌带断面可能为非圆状态，滴灌带断面形变可影响滴头处水流阻力规律，因此研究滴头局部水头损失应考虑滴灌带断面形变的影响。以往毛管水头损失计算方法一般均为圆形断面管，且其断面形状为恒定值，导致常规方法计算结果经常无法反映真实情况。

近年来，对各种不同类型滴灌管和滴灌带水头损失的研究较多[2-5]，以往关于滴灌带水头损失的研究大都认为毛管断面形状为圆形且是固定不变[6]，没有考虑形状变化对水头损失的影响。Neto等[7]对软质PE圆形管沿程水头损失规律进行了研究，并考虑了高压下圆管断面扩大对沿程水头损失的影响，但其断面形状始终是以圆形为基础。有文献研究了椭圆形管道沿程水头损失规律[8]，但并未说明椭圆断面下局部水头损失规律。由于形状变化的不规则性导致由形变引起局部水头损失规律很复杂，使得变断面条件下局部水头损失研究较少见。数值分析和量纲分析因其各自的优点，在管道水力学研究中被广泛应用[9-12]，因而采用以上两种方法研究变断面滴灌带局部水头损失规律。

基于前期毛管水力计算研究的积累[13-14]，本文借助6种不同滴灌带的灌水试验与数值计算，查询断面形变对内镶式滴灌带局部阻力的影响，比较了滴灌带在圆形和扁平工况下局部水头损失的差异，为滴灌带水力计算提供一定参考。

1 试验材料与方法

如图1标注所示，试验装置主要包括供水装置、压力稳定装置、压力采集装置和输水回水装置。因滴头流量相对毛管流量很小，可忽略滴头出流对毛管水流的影响[10]采取堵塞滴头的方式，以保证滴灌带首末段每个滴头的水力要素一致。滴灌带选用2种：内镶贴片式和内镶贴条式，表1列出了供试6组滴灌带的尺寸。

试验中通过滴灌带首尾压力表测定滴灌带总水头差，通过末端阀门控制滴灌带流量。流量每测1次，用游标卡尺测试滴灌带水平和垂直管径，以记录不同压力下滴灌带的形状变化。滴灌带流量通过末端集水称重确定，每次测100 s，重复4次，保证每次流量误差在2%以内，试验中温度范围为10.0℃～15.6℃。试验结束后将数据分为2组，分别用于验证数值模拟和验证拟合表达式。

2 数值计算及验证

2.1 数值模拟参数设置

为保证数值模拟与试验初始条件相吻合，需对数值模型的几何尺寸和网格类型进行调试。通过试验测试，滴灌带在不同的灌水压力下，其断面尺寸随之改变，为探究滴灌带断面形状与压力及壁厚的关系，对6条滴灌带进行调压灌水试验，同时记录每次压力下滴灌带的水平直径Da和垂直直径Db，并以扁平系数α=Db/Da作为衡量滴灌带断面形状的标准，图2列出了实测滴灌带断面形状与压力的关系。

由图2可知，Db/Da随压力变化而不断变化，表明伴随压力改变滴灌带断面尺寸并非恒定，故在研究其水流阻力时，应考虑其断面形变对水头损失的影响。根据图2，当压力较大时，滴灌带水平直径和垂直直径近似相等，可用圆计算其断面面积；当压力较小时，滴灌带水平直径要大于垂直直径，其断面为不规则的扁平形状。为定量刻画扁平状态下的滴灌带局部水头损失规律，考虑扁平滴灌带断面形状与椭圆相近的事实，本文以不同离心率的标准椭圆近似衡量扁平状态下滴灌带的断面形状。数值模型的几何断面尺寸设为椭圆，椭圆的长轴和短轴分别与实测滴灌带的水平直径Da和垂直直径Db相吻合。本文以扁平系数α=0.9作为区分断面圆形和椭圆形滴灌带的临界值，当0<α≤0.9时，认为滴灌带断面为椭圆形，如图3a～图3c；当0.9<α≤1时，认为滴灌带断面为圆形，如图3d～图3e。

表1 试验滴灌带尺寸

采用混合网格并对网格进行独立性检验，当网格数达到3.0×105时，网格数的增加引起的模拟值偏差小于1%，认为网格已满足独立性要求，网格取值范围为3.25×105～4.85×105。根据实测水流流速计算水流雷诺数，雷诺数数范围为954～19 136，滴灌带水流流态处于层流区、过渡区和光滑紊流区，故在数值计算中不计边壁粗糙度的影响，边壁粗糙厚度设为0，粗糙度常数设为0.5。以实测毛管水流流速值作为模拟入口初始流速，毛管出口设为自由出流。紊流选用Realizable紊流模型，层流采用laminar模型。质量及动量守恒控制方程参见文献[15]。

2.2 数值模拟验证

为检验数值模型在圆断面和椭圆断面滴灌带水头损失研究中的可靠性，分别将2种工况下的模拟值与实测结果进行对比。由于6种滴灌带壁厚各异，其中B4壁厚最薄，其断面在微弱压力下即膨胀至圆形，故选B4实测值检验圆断面工况的模拟结果；而B6壁厚最大，即使在较大压力下，其断面仍处于扁平状态，故选B6实测值检验椭圆断面工况的模拟结果。其余4组实测结果用于验证拟合公式。图4列出了B4和B6实测与模拟结果，根据图4所示，滴灌带总水头损失实测值与模拟值较吻合，其中B4滴灌带实测值与模拟值平均相对偏差为3.3%，B6滴灌带总水头损失模拟值与实测值相对偏差为8.5%。相较滴灌带B4，滴灌带B6实测值与模拟值偏差更大，分析原因认为B4滴灌带断面为圆形，模拟滴灌带断面尺寸与实际尺寸非常接近，故其实测结果与模拟结果偏差较小；对于B6滴灌带，其模拟中的几何断面尺寸为标准椭圆形，而实际中的B6滴灌带的断面形状为近似椭圆并非标准椭圆，实际滴灌带断面对于标准椭圆形的偏离会使水力半径减小，增加实测水头损失，导致实测值略大于模拟值，但平均相对偏差在计算允许范围内，因此认为数值模拟结果可较真实反映实际情况。

3 结果分析

3.1 变断面滴灌带局部水头损失计算的数学模型

通过对数值模拟验证分析，认为数值模型可以较好反映不同断面形状滴管带水流阻力问题，故以数值模拟代替试验，对18组不同模拟尺寸滴灌带进行研究。滴灌带外径分别取20、16、12 mm，壁厚取0.11～0.83 mm，滴头长取20～60 mm，滴头宽取3～8 mm，滴头厚取0.5～3 mm，滴头间距取0.3 m，滴灌带长5 m。选择内镶贴片式和内镶贴条式2种滴头，共18组滴灌带，其中9组为圆断面，9组为椭圆断面，18组滴灌带断面尺寸如表2所示。

表2 模拟滴灌带断面尺寸

量纲分析作为理论研究的常用工具在水力学中被广泛应用，尤其是复杂关系的多因素研究，其不但能强化研究理论价值，还能减少工作量。本文首先建立基于量纲分析的滴灌带局部水头损失的结构关系。首先选取滴灌带局部阻力的影响因素，将各因素列于式(6)。

hj=φ(El,Eh,Eb,Da,Db,v,g,υ)

(6)

式中,Da、Db为滴灌带水平与垂直内径(m)；hj为滴灌带局部水头损失(m)；El为滴头长度(m)；Eh为滴头厚度(m)；Eb为滴头宽度(m)；υ为水流运动黏滞系数(m2·s-1)；v为滴灌带水流流速(m·s-1)。

量纲分析首先要在多个物理量中找出基本量，一般量与基本量之间建立无量纲π项，由式(7)确定π项中分子分母指数：

(7)

式中，x1、x2、x3为基本量；xn-m为一般量；n、m分别为总物理量个数和基本量个数；a、b、r为指数。本文将几何量滴灌带水平内径Da和运动量毛管流速v作为基本量，7个一般量与基本量组成π项，通过式(7)确定π项的相关指数，整理后得滴灌带局部水头损失无量纲数学模型式(8)：

(8)

式中，hj/Da为滴灌带局部水头损失；El/Da、Eh/Da、Eb/Da为滴头尺寸；Db/Da为滴灌带断面形状；gDa/v2为弗劳德数；υ/Dav为雷诺数。

将18组滴灌带模拟值代入式(8)并取对数，通过SPSS回归分析，得到滴灌带局部水头损失计算表达式(9)：

(9)

表3 相关项回归分析结果

式中，R2=0.92。由上式可知，滴灌带局部水头损失与滴头尺寸、滴灌带断面尺寸以及弗劳德数相关，而雷诺数对其影响较小。根据表3中的回归分析结果，只有雷诺数对滴灌带水头损失影响未达显著水平，其余各项均对滴灌带水头损失构成显著影响。

将水流运动粘滞系数和重力加速度分别赋值，其他系数进行相应的化简整理，如式(10)：

(10)

将扁平系数α=Db/Da带入表达式(10)并化简整理，式(10)简化为式(11)：

(11)

3.2 模型验证

为检验拟合表达式在滴灌带圆断面和椭圆断面2种工况下的计算准确性，采用B1 、B2、 B3、 B5实测结果对其进行验证。在低压条件下，4条滴灌带断面形状近似为椭圆，用于检验椭圆工况公式计算结果；在高压条件下，4条滴灌带断面形状为圆形，用于检验圆工况公式计算结果。图5为滴灌带在圆形工况下实测结果与计算结果对比图。从图5可以看出4组滴灌带计算结果与实测值比较吻合，B1滴灌带平均相对偏差为8.3%，B2滴灌带平均相对偏差为11.3%，B3滴灌带平均相对偏差为9.1%，B5滴灌带平均相对偏差为6.7%，4组滴灌带平均相对偏差均在10%左右，表明计算值能较准确反映滴灌带水头损失变化规律。图6为滴灌带在椭圆工况下实测结果与计算结果对比图。从图中可以看出， B1、B2滴灌带计算值与实测值较吻合，平均偏差均小于10%；B3、B5计算值与实测值偏差较大，平均相对偏差超过了20%。通过上述分析，滴灌带水头损失计算值与实测值在圆形工况下较吻合，其计算值与实测值偏差的波动幅度较小，断面非圆形滴灌带计算值与实测值偏差的波动幅度较大。这主要是由于在滴灌带扁平时断面形状近似为椭圆，但实际情况并不一定是规则椭圆，其形状存在一定随机性，模拟的标准椭圆与真实的非标准椭圆，两者形状的差异导致模拟值与实测值出现偏差。但考虑4组滴灌带总的平均相对偏差为15%，因此认为仍可用拟合表达式粗略计算非圆工况下的滴灌带局部水头损失。

3.3 滴灌带滴头近场水流紊动特性分析

滴灌带局部水头损失与滴头尺寸正相关，其中滴头厚度对其影响最大，其次是滴头宽度，滴头长度对其影响最小，这表明滴灌带局部水头损失主要是由滴头突起引起断面形状的突然减小与突然增大造成的，而滴头长度对其影响不大。滴灌带局部水头损失与毛管断面尺寸负相关，随着滴灌带断面尺寸的增大而减小，其中滴灌带水平内径对其影响较大。为直观分析滴灌带滴头处水流流速分布和湍动规律，对滴头单元进行横向和纵向切面，通过观测每个横断面的流速分布和纵断面的压力分布分析滴头处水流运动规律。从图7a中可看出，滴头上游紧邻滴头前端的区域出现小范围低速区但未出现负值，滴头下游亦出现低速区，此区域流速不但减小且出现负值，滴头下游发生回流和漩涡，表明滴头出口水流紊动强度较入口要大；由图7a还可看出，滴头上游低速区仅发生在第一断面处，滴头下游低速区扰动波及至第七断面，流速仍未恢复至中心对称分布，表明滴头处流速分布的调整主要发生在滴头下游，滴头上游流速分布变化区域要明显小于滴头下游。从图7b中可看出，滴头附近的低压区主要发生在滴头前端顶部区域和滴头末端尾部区域，即发生在断面形状突变处的下游，这与许多学者研究结果一致[6]。水流所受惯性力致使水流在毛管断面形状突变处与边壁分离，进而导致负压的出现并出现环流漩涡。同时主流区输入的能量不断补充至漩涡区，能量传输达到动态平衡，能量消耗持续进行，局部水头损失持续发生。当滴灌带扁平运行时，滴灌带断面面积减小，而滴头断面尺寸不变，滴头断面面积与毛管断面面积之比增大，等同于毛管断面面积不变情况下增大了滴头尺寸，导致局部水头损失增大。因此，滴灌带断面扁平工况下相比圆形工况下的局部水头损失要大。

4 讨论

在给出内镶式滴灌带局部水头损失计算表达式后，为衡量实际工程中滴灌带局部水头损失情况，以管径16 mm滴灌带B1为计算对象，取60 m为计算毛管长度，分别计算圆断面和扁平系数α=0.76的椭圆断面滴灌带局部水头损失值。假定各滴头流量均匀一致，分别取3个流量值。根据滴头流量计算毛管各段雷诺数，并分别计算不同流态下毛管各段沿程和局部水头损失，沿程水头损失计算采用公式(1)、(2)和(3)，过渡区阻力系数采用定值0.04[16]。3个流区局部阻力均采用式(10)计算，依次计算相邻两滴头间的毛管段沿程和局部阻力。最后将所有各段沿程和局部阻力求和得总阻力，结果如表4、表5所示。

表4 圆断面滴灌带沿程与局部阻力对比

表5 扁平系数α=0.76椭圆断面滴灌带沿程与局部阻力对比

根据表4和表5，滴灌带在圆形和非圆工况下运行，沿程和局部阻力差异明显，非圆滴灌带沿程和局部阻力均大于圆形滴灌带；圆形滴灌带局部占沿程阻力比值为0.08～0.12，非圆滴灌带局部占沿程阻力比值为0.11～0.19。滴灌设计中，通常以沿程阻力的10%～20%来估算局部阻力，根据表5分析可知，当水流压力满足使滴灌带断面呈圆形时，其局部占沿程水头损失之比约为10%，当滴灌带断面扁平时，局部占沿程水头损失之比要增大，比值范围在10%～20%之间，可采用中值15%估算滴灌带局部水头损失。

以往在研究滴头局部水头损失时，大多是以圆形管计算，或是基于圆形的扩大圆断面[17-19]。本文通过低压条件下对滴灌带形状的测试，发现滴灌带形状非圆的事实。通过不同断面形状滴灌带局部水头损失的测试，得出滴灌带局部水头损失与毛管断面形状的关系。根据式(10)，滴头局部水头损失与滴灌带扁平系数的0.867次方成反比，即滴灌带越扁，相同条件下滴头局部水头损失越大。再根据表3中的检验结果可知，滴灌带断面形变对滴头局部水头损失造成的影响是显著的，表明滴灌带形状的改变对局部水头损失的影响不可忽略。这与部分研究结果存在差异[1-3]，分析原因认为，本文要研究断面形变对局部水头损失的影响，因此选择的压力环境较低，部分水流处在层流段，而多数学者研究时为了满足毛管水流雷诺数的要求和计算简便，选择了较高的压力，因此产生了不同的结果。根据算例结果分析，实际工程中在计算滴灌带水头损失时，要分低压和非低压两种工况，即要区别对待圆形断面的滴灌带和非圆断面的滴灌带，当低压条件下滴灌带出现非圆断面时，要考虑滴灌带断面形变对滴头局部水头损失的影响，可参考本文所给出的计算表达式，或在圆形管计算的基础上，适当增大局部水头损失所占比例。