钢衬钢筋混凝土压力管道开裂机理研究
2021-04-28崇银鹏
崇银鹏, 李 扬
(湖北工业大学土木建筑与环境学院, 湖北 武汉 430068)
目前钢衬钢筋混凝土管道结构形式在国内外的水电站工程实践中被广泛应用[1-4],主要作为坝体下游面压力管道使用。钢衬钢筋混凝土结构具有承载能力强,耐久性较好等一系列技术先进性以及较易施工的特点[5],在我国各大水电站工程广泛应用,例如中外闻名的三峡、李家峡、五溪口、东江等水电站中都有采用。这种结构形式运用到混凝土坝下游面,极大减少对于坝体主体结构承载性能的影响,并且在实际施工布置中又能避免坝体混凝土浇筑与钢管的安装之间的相互干扰[6],证实了该结构良好的操作可行性。但是这一结构需要满足长期使用条件,必然需要深入探究耐久性,并提出合理的解决方法。结构裂缝发展状况对于耐久性具有较大影响,而对于钢衬钢筋混凝土压力管道而言,研究管道裂缝发展规律并能有效控制裂缝发展是增强其耐久性的关键所在。相关工程领域的研究人员提出两种思路:一是通过探究构件在相应实际工程应用当中的裂缝发展情况,如考虑管道摩擦接触特性[7]和外包混凝土受拉软化特性[8]等;二是通过研究新材料和新工艺或者新构造设计方式,如引入钢纤维混凝土[9],钢-聚丙烯纤维混合混凝土[10]以及预应力混凝土[11]等,之后围绕管道构件测定出应变情况并计算其应力,总结试验过程当中的裂缝发展情况,结合相应的规范给出与裂缝发展机理相关的公式[12-13]来为工程实际裂缝控制提供指导。上述相关文献虽然较为完善地从多角度考虑并分析不同情况下的裂缝发展机理,但没有探讨径向位移与裂缝发展分布机理之间的关系,忽略多次循环加载作用下的管道裂缝发展分布情况。据此,从内部钢筋钢衬影响因素出发,并考虑加载过程外壁径向位移变化情况与裂缝发展分布之间的关系,通过多组模型进行相关试验,补充探讨多次循环加载作用下裂缝发展分布情况,紧密结合ANSYS有限元模型并进行对比分析,总结发展机理并为进一步裂缝控制提出相关的解决措施。
1 模型试验概况
1.1 模型设计
以某大型水电站工程中混凝土大坝下游面钢衬式混凝土压力管道为实际工程背景,该工程中,坝体高度为160 m,厂房坝段宽30 m,实际管道直径为10.5 m,外包混凝土厚度为1.5 m,管道剖面形状呈现为上圆下方,内部配筋布置依据SL191-2008《水工混凝土结构设计规范》[13]以及GB 50010-2010《混凝土结构设计规范》[14]。沿着管径环向布置三层钢筋,每层间距控制为200 mm,混凝土保护层厚度设置外层钢筋处100 mm,内层钢筋处80 mm,基于实际管道中间3/4处作为试验模型依据。
1.2 试验模型制作
由于实际工程中的钢衬钢筋混凝土管道为大尺寸的构件,为便于试验研究,遵循几何相似原理设计试验构件,对于实际工程中钢衬混凝土管道构件按26.25∶1比例缩小为试验管道构件[15-16],构件长度选定为220 mm。此外忽略自重对构件变形的影响。试验组为4组管道模型,分别记作ABCD四组。每组包含两个对比模型,共计8个管道模型。A组与B组、C组与D组钢衬厚度相同,钢筋直径不同;A组与C组、B组与D组钢衬厚度不同,钢筋直径相同,通过自主制作的加载装置模拟水压力作用,进行对照试验。模型参数设置如表1所示。

表1 管道模型参数与配筋设置对照
此次试验混凝土采用C30混凝土,养护28 d,受力钢筋和架立钢筋采用HPB300钢筋,屈服强度标准值为300 MPa,设计值则为270 MPa;内壁钢衬板选用Q235钢,屈服强度标准值为235 MPa,设计值则为215 MPa。此外管道试验模型横向截面外轮廓是上圆下方,类似于马蹄形状,内轮廓呈现正圆形,具体尺寸可参见图1管道模型尺寸示意图。
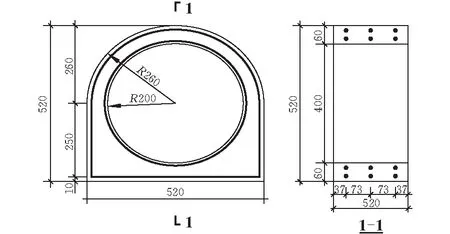
图 1 管道模型尺寸示意图
钢衬板布置在管道内壁上,承担内水压力。内部配筋沿着管道径向方向上设置为两层,内层钢筋与界面内轮廓相同,为规则圆形状,外层钢筋则设置方圆形状,并且每层配筋沿着纵向长度方向配筋间距设置为73 mm,一共为三道,并且通过纵向钢筋相连接。
1.3 试验测点布置
由钢衬钢筋混凝土压力管道布置方式可知,其圆形部分在坝下游面水平面以上位置,下部方形部分与坝体施工之时所预留出锚筋浇筑在一起[17-18]。所以构件的变形和裂缝大部分出现在圆形管身,此次试验着重观测分析上圆形部分的应力应变情况。测量角度则以构件几何中心点为原点建立极坐标系,上下部交接处为0°和180°,角度布置如图2所示。钢筋和钢衬应变片布置情况分别如图3、图4所示。

图 2 构件测量点角度布置图
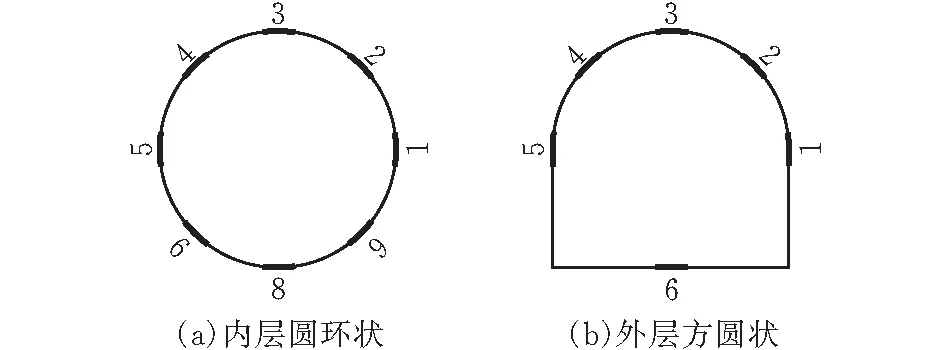
图 3 钢筋应变片布置示意图
如图4所示,混凝土应变测点布置图,需要指出的是应变片距管道构件边缘控制在25 mm,即扣除最外一道径向钢筋保护层厚度,保持与内部配筋位置一致。

图 4 混凝土应变片布置图
试验在直接测量应变的基础上,同时也进行了管道外壁径向位移值的测定。测定方法是沿着外壁圆弧每隔45°放置一个径向位移计来测定全方位的位移数据,具体布置效果如图5所示。

图 5 管道外壁径向位移布置图
2 试验结果及分析
2.1 试验模型裂缝发展情况
通过采用环形套筒液压加载方式以0.2 MPa的增量逐步从0.3 MPa加载到2.3 MPa,每加载一步,记录相关数据和裂缝发展情况。可以观察到各组试验模型混凝土出现初裂贯穿裂缝,随着荷载的增加,管壁四周不断产生放射状裂缝,各条裂缝基本分布在模型圆形管壁上。此外本试验的模型在达到最大设计内水荷载2.3 MPa之后,卸载至0.2 MPa再逐步加载到最大设计内水压,循环这一过程3次,在循环次数不断增加时,试验模型在达到某一内水荷载时,裂缝条数不变,但裂缝宽度不断增大。原因在于钢衬混凝土内部配筋在循环作用下呈现一定的屈服状态,此时钢筋应力保持稳定而塑性应变不断增加,但钢筋与混凝土之间的相互粘结作用使得混凝土的应变随之增长,最终出现裂缝数量不变反而裂缝宽度不断增大的状况。试验各组模型开裂情况(图6),相同字母组1,2模型参数完全相同,以反映试验情况的离散性,可以发现在从初荷载逐步加载到最终荷载这一过程中,四组模型的裂缝几乎都分布在钢衬上圆部分的管道上,而在循环荷载作用过程当中则主要在下方方形部分出现裂缝。

图 6 各模型最终裂缝分布图
由表2中给出本次试验当中最终测得的裂缝相关参数以及模型初裂荷载情况。对比A、C组模型以及B、D组模型裂缝分布,可以发现:在控制内部配筋率一定的情况下,提高钢衬厚度,能够降低最终裂缝条数,同时能够有效提高初裂荷载值,但裂缝其他参数如平均宽度、间距以及最大宽度将明显增大。对比A、B组模型以及C、D组模型裂缝分布,可以发现:在控制钢衬厚度值一定的情况下,配筋率提高能够有效降低裂缝在加载过程中的平均间距、平均宽度以及最大裂缝宽度值,并且初裂荷载显著提高,裂缝条数增加。
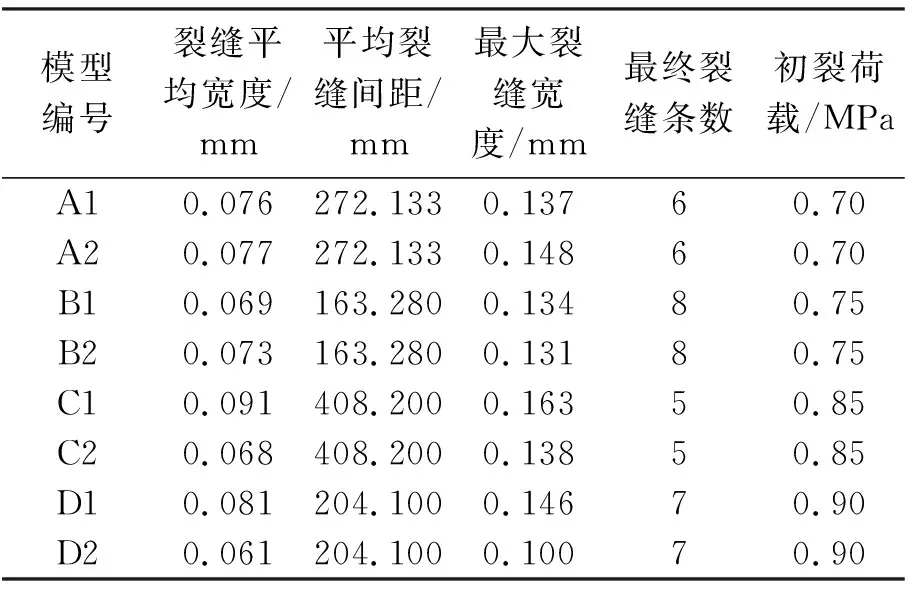
表2 管道模型的裂缝开展实测值
2.2 试验模型不同角度管壁的径向位移
根据对称原则,取0°、45°和90°位置上测得的给定荷载加载条件下管道模型混凝土外表面径向位移值。给出四组试件圆形管壁的径向位移随荷载变化的关系如图7所示。从图中可以看出:混凝土开裂前,管道的径向位移较小,且随内水压力的增大,径向位移变化不大,管道圆形区域各处的径向位移相差不大,此时管道模型的整体刚度较大;混凝土开裂以后,管道模型的整体刚度降低,裂缝条数越多,整体刚度降低越多,管道的径向位移随内水压力增大而快速增大。比较四组管道模型0°、45°和90°处径向位移随内水压力的变化规律,发现混凝土开裂以后,在同一荷载加载条件下,管道构件出现贯穿裂缝之后由之前各位置径向位移相差较小的情况转变为不同角度位置径向位移差异较大,在0°位置径向位移处于最大值,该位置裂缝发展最为迅速,而在90°位置径向位移值最小,裂缝发展较为缓慢,总体呈现出角度越大,裂缝发展越慢的趋势。

(a)A模型
3 有限元模型对比分析
3.1 模型本构关系
在通用有限元分析软件ANSYS中,钢筋混凝土建模形式分别为整体式建模,分离式建模,以及分离式并考虑滑移和粘结建模[19]。针对所研究钢衬式管道构件,取原管道斜直段的断面建立有限元模型,长度方向取1 m,设计最大内水荷载为1.23 MPa,按静水压力作用考虑。采用分离式建模方法,混凝土部分采用solid65单元,钢筋为link180单元,钢衬单元考虑选择shell181单元[20-21],该单元可以很好的适用于非线性分析下的构件的大变形情况。此外在实际试验当中,随着内水荷载的不断增加,构件表现出较为明显的塑性状态,但是裂缝的发展导致构件不断丧失塑性性能直至内部配筋屈服并发生破坏,因此利用ANSYS参数化建模的优势,建立混凝土塑性损伤模型。混凝土的本构关系选取了多线性随动强化模型(MISO)并在破坏准则当中关闭压碎选项,以防止计算出现不收敛的情况发生,而钢筋的本构关系则选取双线性强化模型(BISO),单元节点方面则采用钢筋单元首尾和混凝土单元共享节点,两者之间的刚度矩阵分开来求解。通过这一方式,当混凝土某一单元的应力超过了开裂应力,则只需将材料的本构关系矩阵加以调整,无需改变单元形式或重新划分网格,与其他模型相比,该模型结果较符合实际情况。
建模时的混凝土与钢衬以及钢筋的详细物理参数如表3所示。几何建模时模型尺寸选取试验模型的数值。此外模型形状倾向于上圆下方的形状,简化实际模型中与管道连接的锚固底座为固定支座。荷载加载方法采用多荷载步方式从0.3 MPa加载到2.3 MPa,有限元效果图见图8。

图 8 有限元模型图

表3 管道基本参数
3.2 仿真计算值和试验值分析与对比
以管道模型管腰0°处钢筋钢衬为例,以建立的有限元模型为基础运行分析,可得图9各组试验模型内外层钢筋钢衬的仿真计算值和试验值的对比情况。可以发现,各模型在达到初裂荷载之前,钢筋钢衬应力值较低且相差不大,初始阶段在4 ~6 MPa之间,并以5 MPa左右速度缓慢增长,该阶段管道施加的大部分内水荷载由外包混凝土来承担,内部配筋则承担较少的荷载。对比A、B或C、D组,配筋率增加1%,内外层钢筋应力均降低约0.3~0.4 MPa,但钢衬应力值基本相等;当钢衬厚度增加1 mm时,钢筋应力基本相等,但钢衬应力降低约0.6~0.7 MPa。这一结果表明在未达到初裂荷载阶段,相比于配筋率,钢衬厚度的增加能够更有效的降低内部钢筋的应力。
逐步加载达到初裂荷载,钢筋钢衬的应力迅猛上升,在此阶段内外层钢筋钢衬的应力增长速度以及趋势各不相同。外层钢筋增速从初始的40 MPa放缓至20 MPa,之后又回升至30~40 MPa增速直到试验结束,而内层钢筋应力增长相对稳定,以20~30 MPa速度增加,而钢衬应力在此阶段保持10~20 MPa速率上升,但在加载最后阶段速度大幅增加,达到约30 MPa,在这一阶段对比A、B或C、D组,配筋率增加1%,内外层钢筋应力从初裂阶段开始时降低10~20 MPa左右,总体上随时间推移降低数值不断增加,最大可达到60~70 MPa左右,这表明在较高的外荷载水平下,提高内部配筋率能够有效降低管道内钢材的应力并且改善承载能力,提高抗裂水平。此外对比A、C或B、D组,钢衬厚度增加1 mm,钢衬应力则在整个过程当中稳定降低30 MPa左右,整体呈波动上升趋势,这表明:相比配筋率,在较低的外荷载水平下,提高钢衬厚度能够更有效地降低管道内钢材的应力,从而增强抗裂能力,提高承载水平。
对比分析也表明仿真计算值和试验数据较为吻合,随着内水荷载的不断增长,两者数值的变化趋势也基本相同。在钢筋应力方面该有限元模型能够与实际模型相互印证,在此基础之上引入相关更多影响因素,可以结合相关裂缝计算公式来计算出管道裂缝宽度深度数值,即可得到裂缝分布机理。

(a)A模型
4 结论
1)影响钢衬钢筋混凝土管道开裂荷载的主要因素为配筋率和钢衬厚度。在给定相同配筋率前提下,减少内部配筋间距,提高配筋率,对于钢衬钢筋混凝土构件而言,其裂缝条数明显增加,但裂缝宽度也显著减少。
2)在循环加载过程中,增加循环次数,裂缝条数不变,但裂缝宽度不断增大,表明钢衬混凝土内部配筋在循环荷载作用下出现一定的屈服。
3)从径向位移来看,管道构件裂缝发展机理可以分为两个阶段,第一阶段是管道构件混凝土出现贯穿裂缝,上圆部分径向位移随荷载加载变化幅度较小,且该处范围内各个位移值相近,表明其内部裂缝正逐步发展均衡;第二阶段是当荷载施加到一定值,管道出现放射状贯穿裂缝,管道外壁径向位移随内水压力增大而大幅度增大,并且裂缝数量随着径向位移的增大也不断增长。
4)在达到开裂荷载后,提高钢筋配筋率能够在较高的内水压力下,增强管道承载能力和减少裂缝发展;提高钢衬厚度则能够在较低内水压力水平下增强管道承载能力和抗裂性能。
5)有限元仿真结合实际模型试验方法可以有效探究钢衬钢筋混凝土管道的裂缝发展分布规律,此外通过合理有限元建模也能够预测出管道结构承载特点和受力基本状况,对于后续管道设计有较强的指导意义。
