区间数多属性决策的两种新算法
2021-04-28朱国成陈利群
朱国成, 陈利群
(广东创新科技职业学院 通识教育学院, 广东 东莞 523960)
0 引言
多属性决策理论在解决复杂排序问题的多准则决策中扮演了重要角色,已经成为解决现实生活中产品优选、投资决策、人才引进、教师教学评价等问题的重要工具[1-8]。在用区间数表征属性值时,面对的首要问题是区间数排序,目前有关此类研究的文献非常丰富,例如,徐泽水等[9]建立了一个区间数可能度模型,并依此模型构建了一套多属性决策算法;朱方霞[10]采用类似TOPSIS的方法,利用相离度相关理论,通过计算各方案与理想方案的贴近度大小对方案进行排序;朱国成等[11]针对由效益型属性构成的方案,利用区间数积型贴近度模型对不同方案对应的同一属性两两测度,通过统计测度大于1的结果鉴定方案优劣。本文在文献[9-11]研究的基础上做进一步延展:针对文献[9]方案中属性具有效益型与成本型两种特征,利用文献[11]中区间数积型贴近度公式分别制定不同排序方法;结合文献[10]TOPSIS排序思想,建立方案综合属性值求解模型,利用区间数积型贴近度公式算出每个方案的综合属性值,对每个方案的综合属性值进行比对,并把优选结果分别与文献[9,10,12]的排序结果进行比较,对比结果说明了本文提出的方法是科学有效的。
1 基础知识

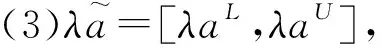
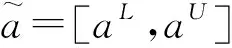




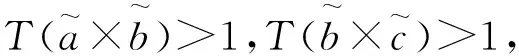

2 两种决策算法
2.1 两两测度属性值法
2.1.1 两两测度属性值法的应用步骤
根据定义3,两两测度属性值法的基本步骤如下:
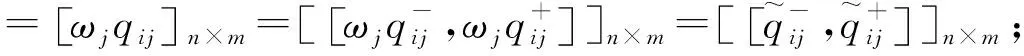

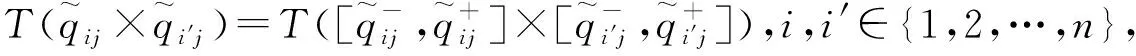
步骤5 建立决策模型:
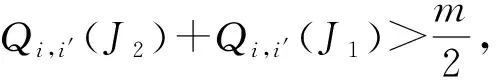
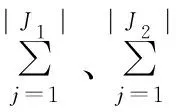
1) 若S+(ai,ai′)>S-(ai,ai′),则方案ai优于方案ai′。
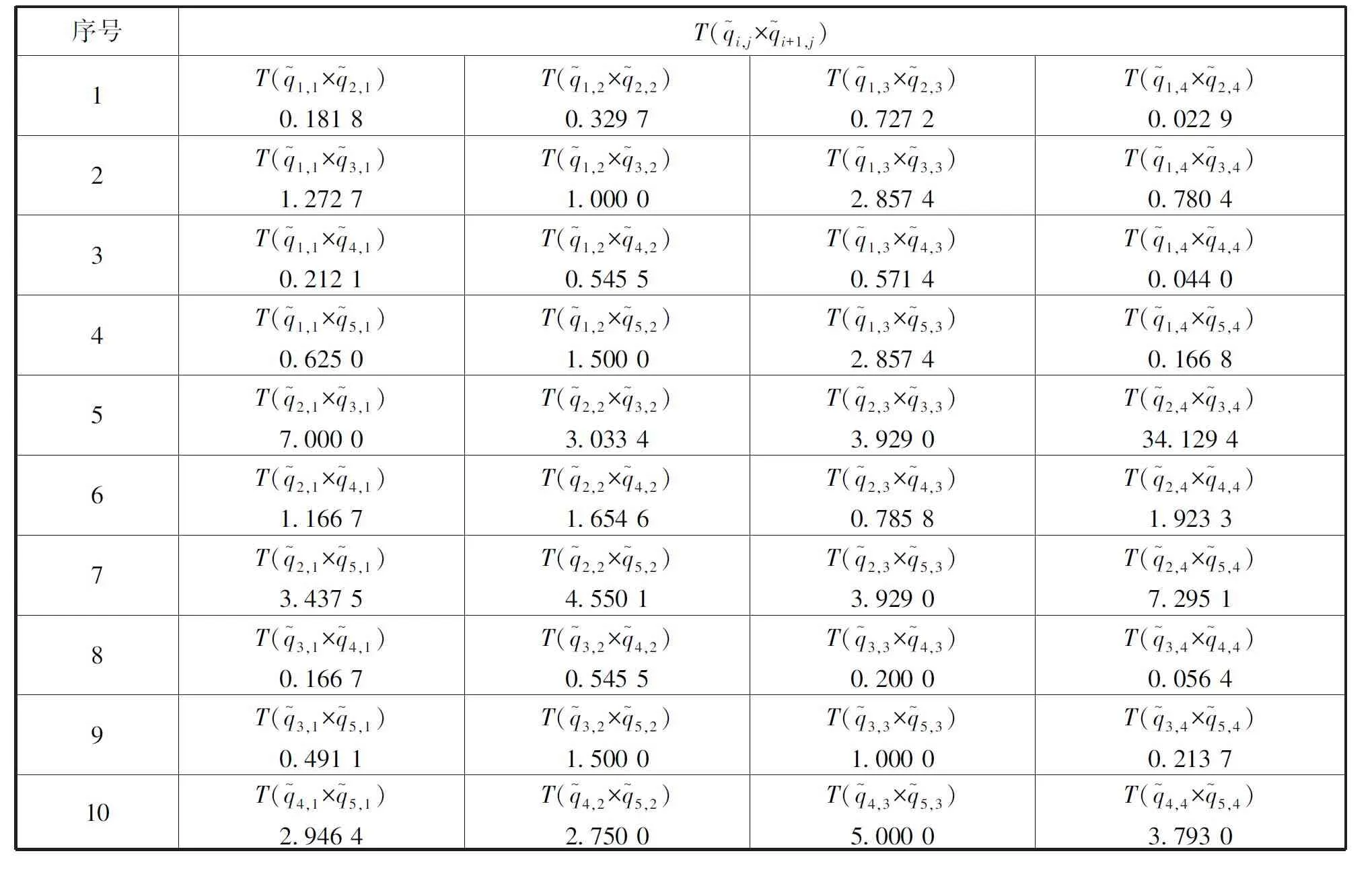
2) 若S+(ai,ai′) 3) 若S+(ai,ai′)=S-(ai,ai′),则方案ai与方案ai′等同。 步骤6 比较决策结果; 步骤7 结束。 2.1.2 案例分析 为了说明本研究提出方法的合理性,现将研究结果与文献[9]在决策方法上进行系统比较。 例1 为了开发新产品,准备了5个投资方案,用符号ai(i=1,…,5)表示,4个属性用符号cj(j=1,2,3,4)刻画,意义见表1。权重ω1=0.230,ω2=0.142,ω3=0.192,ω4=0.436,c1、c4为成本型属性,c2、c3为效益型属性,具体属性分值见表1。 表1 投资方案属性值单位:万元 文献[9]中的决策算法:为了能够使决策矩阵评价数据自由运算,要做到以下几点:首先,对决策矩阵中的数据先进行规范化处理;其次,在求出各方案的综合属性值后,采用区间数可能度公式算出方案之间的综合属性值可能度;最后,通过可能度互补矩阵算出可能度矩阵的排序向量,并根据排序向量分量值的大小对方案进行排序。 本文算法:首先,由表1得出决策矩阵q,并通过加权得到加权矩阵qωj。 表2 属性测度表 再次,以比较方案a1,a2优劣为例进行说明。由表2得Q1,2(J1)=2,Q1,2(J2)=0,Q1,2(J1)+ S+(a1,a2)>S-(a1,a2),故方案a1优于方案a2。同理可得:a1>a3,a1>a4,a1>a5,a2 2.2.1 决策步骤 根据定义3的陈述,类TOPSIS法的基本步骤如下: 步骤3 确定理想属性值公式如下: 步骤4 利用定义2,在成本型与效益型两种情形下测度方案ai的属性值与正负理想属性值,最后算出每个方案的理想综合属性测度值S(ai),i∈{1,2,…n}, S(ai)=S(ai(J1))+S(ai(J2)),i∈{1,2,…n}, (3) 步骤5 根据S(ai)大小对方案ai排序,由S(ai)计算公式可知,S(ai)越大,方案ai越优。 步骤6 比较决策结果。 步骤7 结束。 2.2.2 案例分析 为了方便说明该方法的合理性,现将该研究结果与文献[10]的研究结果进行比较。 先介绍文献[10]决策算法的基本步骤: 首先,利用相离度公式分别算出各个方案与正理想方案和负理想方案的总相离度; 其次,利用相对贴近度公式算出每个方案与理想方案的相对贴近度; 最后,根据贴近度大小进行方案排序。 这里继续使用文献[9-10]中提及的案例1进行说明。 本文算法: 决策前两步与两两测度属性值法的决策前两步一致,故可以直接进入第3步,首先,确定理想属性值: (4) (5) (6) (7) 其次,为了方便观察,利用式(3)建立方案的测度表(见表3)。 由表3得:S(a1)=56.277 9,S(a2)=12.430 6,S(a3)=45.934 5,S(a4)=12.655 1,S(a5)=13.810 3,故方案排序为a1>a3>a5>a4>a2,各方法的排序结果见表4。 表3 投资研究方案的测度表 表4 排序法及结果 通过对比可知,本文构造的两种排序方法都是有效的。 本文研究了区间数多属性决策问题的两种算法,并探讨了在区间数积型贴近度模型测度下的多属性决策算法。两两测度属性值法针对的是相同属性下不同方案的测度问题,优点是无需对决策矩阵数据进行规范化,同时,相较于文献[9]中多次对属性数据进行集结、运算,本文提及的两种算法对保留决策数据信息更为有利。因为本文中属性数据计算形式明显少于文献[9],对于处理方案中具有“一票否决”式重要属性时(也就是说该属性的好坏直接决定方案优劣,例如在评价优秀教师时,师德这一选项就是“一票否决”制)不适合。因为简单的属性个数优劣比较无法突出这一重要属性在方案中的决策价值。利用类TOPSIS法对问题进行排序,首先要确定正负理想属性值,其次再对属性值与正负理想属性值进行测度,最后求得方案的理想综合测度值,通过比较方案的理想综合测度结果的大小对方案进行排序。整个决策过程类似文献[10]中的TOPSIS方法,故该方法命名为类TOPSIS法。通过与文献[9,12]决策结果比较可知,本文构造的两种决策方法都是可行的,由此也进一步丰富了属性信息由区间数构成的多属性决策理论。未来,在解决由区间数构成属性值的多属性决策问题中,利用区间数积型贴近度公式求解属性权重方法将是一个有意义的研究课题,笔者将对此问题作进一步的深入研究。



2.2 类TOPSIS法

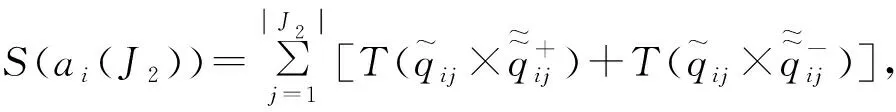
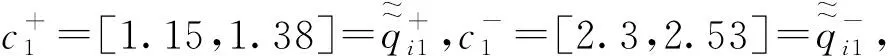
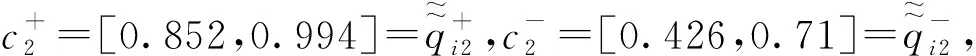
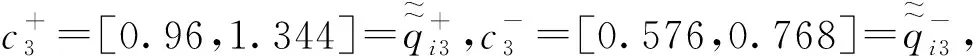


3 结语
