托马斯效应的简单诠释

杨 一，李秀玲，罗成林

(南京师范大学 物理科学与技术学院，江苏 南京 210023)

为解释碱金属光谱的精细结构和反常塞曼效应，乌伦贝克和哥德斯密特提出了电子自旋的假设，尽管与观察结果定性相符，但在数值上，根据电子自旋和轨道相互作用公式计算的碱金属原子光谱的精细结构却比实验值大了一倍，因此这种假设受到了许多人的质疑.直到托马斯指出原子实绕价电子转动的价电子参考系中的自旋轨道相互作用转换到价电子绕原子实运动的原子实参考系时需考虑相对论效应引起的坐标系的进动[1,2]，即托马斯进动，才真正确认了电子自旋的概念，并得到计算出了与实验值相一致的精细结构数值.但对于托马斯进动角速度的推导，常用的微分角度利用连续二次洛伦兹变换的方法过于繁琐，也不易理解，本文采用积分的角度，从电子绕行原子实一周时，在原子实参考系和电子随动参考系中的角度差出发，使计算过程简洁明了，并呈现出清晰易懂的托马斯进动图像.

1 问题的引入

在原子物理教学中，自旋-轨道相互作用是理解原子精细结构的核心物理概念. 按照电磁学理论， 电子自旋-轨道相互作用的能量U=-μs·B′(μs是与自旋相联系的磁矩，B′是电子感受到的由自身轨道运动而产生的磁场).在主流教科书上[3,4]，该磁场的计算方法如下：原子的价电子绕着原子实做轨道运动，根据运动的相对性，在相对于价电子静止的坐标系中，带正电荷的原子实则以相同大小的速度绕电子运动(见图1)，从而使电子感受到一个磁场,且该磁场的方向与电子轨道运动角动量的方向一致.因此，由毕奥-萨法尔定律可以很容易地算出[4]

(1)

式中，Z*是原子实的有效电荷数，r是电子轨道运动的半径，v是电子绕原子实运动的速度，E是原子实作用于电子的静电场.但是用这个磁场计算出来的能量与实验光谱不符， 且正好比观测值大一倍，也就是说，电子感受到的磁场应是上式计算值的1/2. 历史上，这个结果曾对电子自旋概念的确认带来很大困扰.

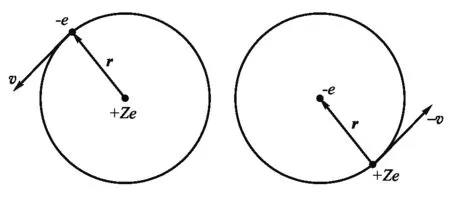
O系观察 e系观察图1 电子在轨道运动中感受磁场示意图[3]

1926年，托马斯[1,2]发现了理论与实验不符的关键. 原来，静止的原子实参考系(简称O系)与做加速运动的电子参考系并不等价. 在整个原子系统中，由于原子实质量远大于电子质量，故可以认为原子实保持静止而仅有电子在运动, 因此，O系是惯性系. 然而，电子受与其速度垂直的电场力作用下作圆周运动，存在向心加速度，电子本身则是一个非惯性转动参考系.起初， 经典物理理论忽略了原子实参考系和电子参考系的差别，认为它们是等价的， 故将在电子参考系中计算得到的电子自旋-轨道相互作用能量等同于O系中的自旋-轨道相互作用能量，致使理论值比实验值大1倍. 托马斯考虑了原子实参考系和电子参考系的非等价性,此外，他还注意到，由于电子自旋概念的引入，意味着电子有一个自旋轴，此自旋轴的方向即是电子自旋角动量ps方向，如图2(a)所示. 所以，电子参考系是一个包含自旋轴的参考系(简称e系, 其自旋轴记为z′轴).需要强调的是，毕奥-萨法尔定律只在惯性系中成立. 在e系中，由于电子做圆周运动，为了确保e系为惯性参考系， 只能假设它瞬时相对于电子静止. 电子运动到下一时刻，e系将与电子脱离，于是，必须重新选一个e系，使之与电子保持瞬时静止. 这就导致e系相对于O系有一个转动角速度(在教科书及参考书中，此物理图像并不是一目了然的)，称之为托马斯进动. 但光谱精细结构实验值是在O系中测量得出，其理论值应该用O系中的实际进动频率进行计算，这个进动效应的净效果恰好使电子感受到的磁场强度为式(1)计算值的一半，这就是由式(1)求得的磁场强度需乘以1/2因子的来源.

托马斯进动的发现，使电子自旋假说与实验完美符合，从而确认了自旋概念，在物理学发展史上具有重要意义. 遗憾的是，托马斯进动角速度的理论推导很繁杂[2]，难以在课堂上予以明晰的演算. 为了能让学生理解托马斯进动效应，许多教师付出了艰苦努力，其基本方式仍是沿用Thomas的思路：从微分学的角度进行连续旋转运动的二次洛伦兹时空变换[5,6]，以导出e系相对于O系的托马斯进动角速度，进而求出O系中，电子所感受到的由于其轨道运动形成的磁场.虽然简化了一些步骤，但其推演过程仍然复杂易错，物理图像比较晦涩，不适于在教学过程中应用.为此，H Kroemer[7]曾提出一个描述托马斯进动效应的新思路: 在静止O系中预先引入一个垂直于电子轨道运动方向的磁场，使电子受到新引入磁场的洛仑兹力与电子和原子实之间的库仑力平衡，让电子所受合力为零而作匀速直线运动. 此时，电子可作为惯性参考系予以考虑. 这种方式回避了托马斯进动角速度的概念和计算，直接求出电子自旋感受的磁场，但却需要学生对较为复杂的相对论电磁学有很好的知识储备，仍然不够简单，并且缺乏对托马斯进动物理图像的描述.

经过研究，我们发现完全可以从积分的角度对托马斯进动进行理解和推导，E M Purcell曾给出过相似方法的建议[8]，借助飞机沿多边形飞行的模型进行了托马斯进动的推导，本文则采用更为直接的方法，从电子绕原子实运动时因参考系的差异而产生的角度差入手，展现生动的物理图像，进行简单的推演，易于学生掌握.

2 托马斯进动物理图像的简单描述

在e系中，电子自旋将在磁场B′作用下绕电子自旋轴z′进行拉莫尔进动(如图2(a)示)，根据旋磁比关系,并结合式(1)可知，该拉莫尔进动角速度为

(2)

其中，m是电子质量.但需注意的是，这是电子在e系中绕其自身的自旋轴的拉莫尔进动角速度，但自旋-轨道相互作用能量是在实验室系中获得的.为了一致性，我们应求出在O系中观察到的电子自旋进动角速度.

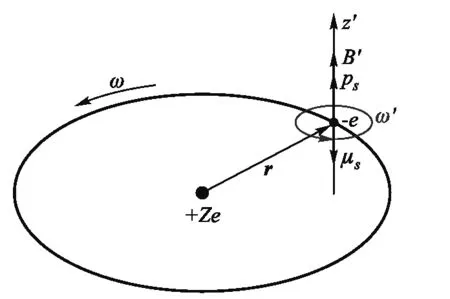
电子自旋由于感受到B′而绕z′的拉莫尔进动

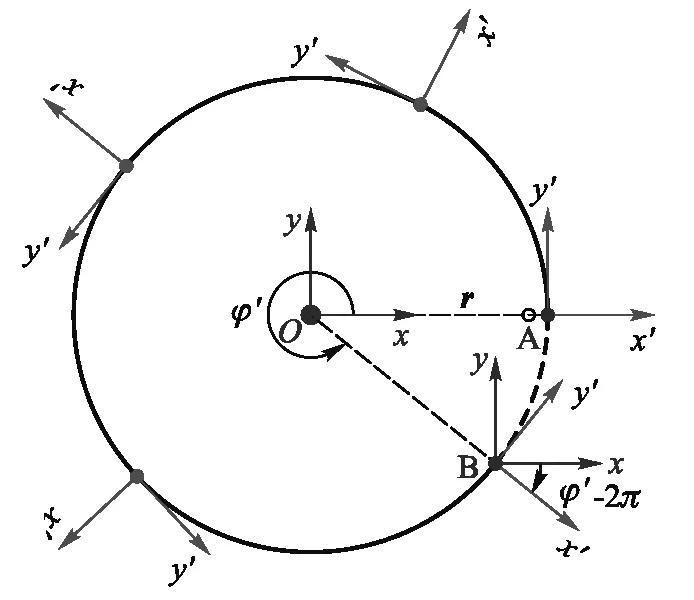
O系(xy)与e系(x′y′)随电子运动的变化图2 托马斯进动物理图像

由图2(b)可见，在电子运动的起始点A处，e系在电子轨道运动平面的坐标轴 (x′,y′) 指向与O系坐标轴 (x,y) 指向一致. 对于O系而言，电子从A点出发，绕原子实运动一周,运动距离l0= 2πr，最后回到A点，e系旋转2π角度，其坐标轴 (x′,y′) 回归到出发时与O系坐标轴 (x,y) 方向一致的情形. 而在相对于电子保持瞬时静止的e系观测，因为电子运动速度始终沿圆周切向，根据狭义相对论运动方向长度缩短的结果，电子绕原子实运动“一周”的距离会收缩为

(3)

而电子速度方向始终垂直于半径方向，半径r保持不变，不会收缩. 所以，在e系看来，电子从A点出发，绕原子实“一周”，经过l′的距离，最后只能到达B点，其绕原子实运动所转过的角度为

(4)

因为v≪c，可得

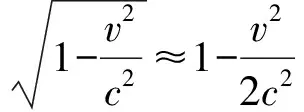
(5)

这表明e系并没有完成2π角度的旋转. 因此，在点B处，e系的坐标轴指向与起始位置A处的坐标轴必然存在角度差。但是，从O系来看，电子绕行原子实一周，旋转了2π角度， e系此时的坐标轴指向应该与起始点A处坐标轴指向相同，即与O系坐标轴指向一致，所以为了方便对比，我们可以将O系坐标指向平移至B点处，图中B处红色坐标系指向即是原子实O系的坐标指向，而蓝色坐标系代表电子随动e系. 显而易见，e系与O系的坐标轴指向之间存在一个(φ′-2π)的角度差，这个角度差的出现说明在电子绕原子实运动的过程中，e系相对于O系会有相对转动 ，也就意味着，O系(实验室系)观察到电子随动的e系有一个相对于自己的进动角速度ωT. 这就是托马斯进动效应的物理图像.

设电子运行一周的时间为T,则有

(6)

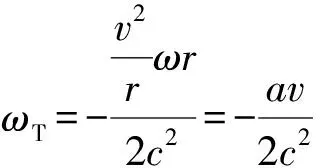
(7)

式中a是电子的向心加速度. 上式写成矢量式，即

(8)

与托马斯的结果比较[5, 9]，发现这正是一级近似下托马斯进动角速度的表示式. 由此可见，从原子实O坐标系和电子随动e坐标系观察电子绕原子实“一周”距离的相对性结果，可以很容易地求出非惯性e系相对于惯性原子实O系的托马斯进动角速度. 与通常采用连续微分过程求托马斯进动角速度的方式不同， 这里是通过电子绕行原子实一周时，O系和e系坐标轴指向形成的角度差的积分效应来导出托马斯进动角速度. 该方法极致简单且托马斯进动的物理图像也可得到更为清晰的描绘，而这正是从积分的角度将托马斯进动角速度的推导简单化和图像的展现清晰化.显然，托马斯进动的起源是纯相对论运动学的，只要有垂直于B′的加速度分量，那么就有一个托马斯进动， 与自旋磁矩在磁场中的常规拉莫尔进动没有关系. 因为电子轨道运动加速度

(9)

所以，Thomas进动的角速度为

(10)

综合来看，在e系中只能观察到B′作用下导致的电子绕其自旋轴z′的拉莫尔进动ω′；而在O系，则在观察到电子绕e系自旋轴作拉莫尔进动的同时， 还会观察到e系自旋轴相对于O系的托马斯进动. 因此，在原子实O系中观察到电子自旋磁矩作拉莫尔进动的实际角速度ωL应该等于电子自旋磁矩相对于e系的拉莫尔进动角速度与e系相对于O系的托马斯进动角速度之和， 即

(11)

(12)

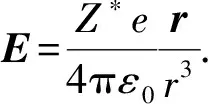
3 小结

托马斯进动效应在物理学发展史上具有重要地位，正是它的发现才确立了电子自旋的概念并实现了碱金属光谱精细结构的定量计算. 虽然，通过对电子轨道运动的微分过程进行连续洛伦兹坐标变换一直是求托马斯进动角速度的基本方法，但是，该方法计算十分繁复，其物理图像也并不是显而易见的. 而本文从积分视角考察电子轨道运动在原子实参考系和电子随动参考系中运动的相对差异性，可给出托马斯进动效应简洁清晰的物理图像，计算过程简单明了. 在教学过程中，我们应该尽可能秉承爱因斯坦的科学精神，那就是：As simple as possible, but not simpler.

致谢：作者感谢郭立波教授、平加仑教授的有益讨论.