基于灰色关联和模糊物元的几内亚湾区综合竞争力评价

李敏，封学军，蒋柳鹏，庄凯

（河海大学港口海岸与近海工程学院，江苏南京210098）

0 引言

“湾区”的概念起源于美国旧金山湾。该地区依托硅谷形成了汇聚科技、创业以及人力资本的全球化聚集港湾。从世界经济发展史看，全球60%的经济总量集中在入海口区域，约75%的大城市、70%的GDP和人口集中在距海岸100 km的海岸带地区[1-2]，国际大湾区已经成为了带动全球经济发展的重要增长引擎和引领技术变革的领头羊，发挥着引领创新、聚集辐射、转型升级的核心驱动作用[3]。

当前针对大湾区的研究方法以区域经济学领域的方法为主，侧重于经济、人口等基础性指标的分析[4]，如：綦鲁明[5]将深圳作为主要研究对象，构建了深圳湾区经济的评价指标体系，得出当前深圳湾区经济处于快速发展期，鲁志国等[6]从土地面积、GDP等反映湾区经济的基础指标入手，评价包含粤港澳大湾区的全球四大湾区的竞争格局，提出了推动湾区经济发展的重点是发挥区域特色和推动体制机制创新。伍凤兰等[7]、马忠新等[8]也运用了不同方法对湾区进行了相关研究。

针对大湾区的研究少有对其综合竞争力评价的方法和成果，也缺乏对非洲是否在若干年后能形成大湾区进行的思考与探讨。本文将提出几内亚湾区的概念，基于湾区具有的共性特征，利用灰色关联投影和模糊物元评价结合的方法通过对纽约湾区、旧金山湾区、东京湾区、粤港澳湾区以及几内亚湾区竞争力进行比较研究，全面地得到五大湾区在竞争中各自的优劣势，并为几内亚湾沿岸国家决策提供相关科学的建议。

1 几内亚湾区的发展现状

几内亚湾是非洲最大的海湾，沿岸地区涵盖6个西非沿海国家和4个中非沿海国家，包括利比里亚、科特迪瓦、加纳、多哥、贝宁、尼日利亚、喀麦隆、赤道几内亚、加蓬，以及湾头的岛国圣多美和普林西比。如图1所示。其三面环陆、海岸线长、经济腹地广的优越地理条件加上具备优先吸收外商投资能力的众多港口城市符合形成湾区的前提基础[9]。

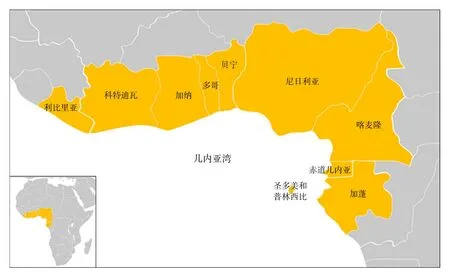
图1 几内亚湾沿岸国家区位图Fig.1 Location map of countries along the Gulf of Guinea

根据世界银行数据统计，几内亚湾沿岸国家的面积仅占非洲面积的0.8%，人口为非洲的2.2%，然而创造了非洲近30%的GDP，其中，尼日利亚GDP总量位居非洲第一，大多数国家GDP增速都超过非洲平均水平。巨大的人口红利，飞速的城市化进程、全球的人口流动以及工业革命使得几内亚湾地区有着十分可期的前景，丰富的自然资源更是使得几内亚湾沿岸国家已经成为世界热点关注的地区。经济全球化和“21世纪海上丝绸之路”倡议的实施，给该地区提供了新的发展机遇。

2 大湾区综合竞争力评价指标体系

指标体系选取和构造的合理性对评价湾区竞争力起着至关重要的作用，总结申勇[2]、吴家玮[10]、田长霖等[11]的研究，同时通过对中国商务部、世界银行、各国商务部、统计局等相关数据分析，建立了大湾区发展竞争力的评价体系，如表1所示。该系统主要由三层指标构成，即第一层：目标层，大湾区竞争力（A）；第二层：要素层：自然资源（B1）、经济条件（B2）、物流条件（B3）、创新科研条件（B4）；第三层：指标层，反应大湾区竞争力的具体形态（C），共17个。

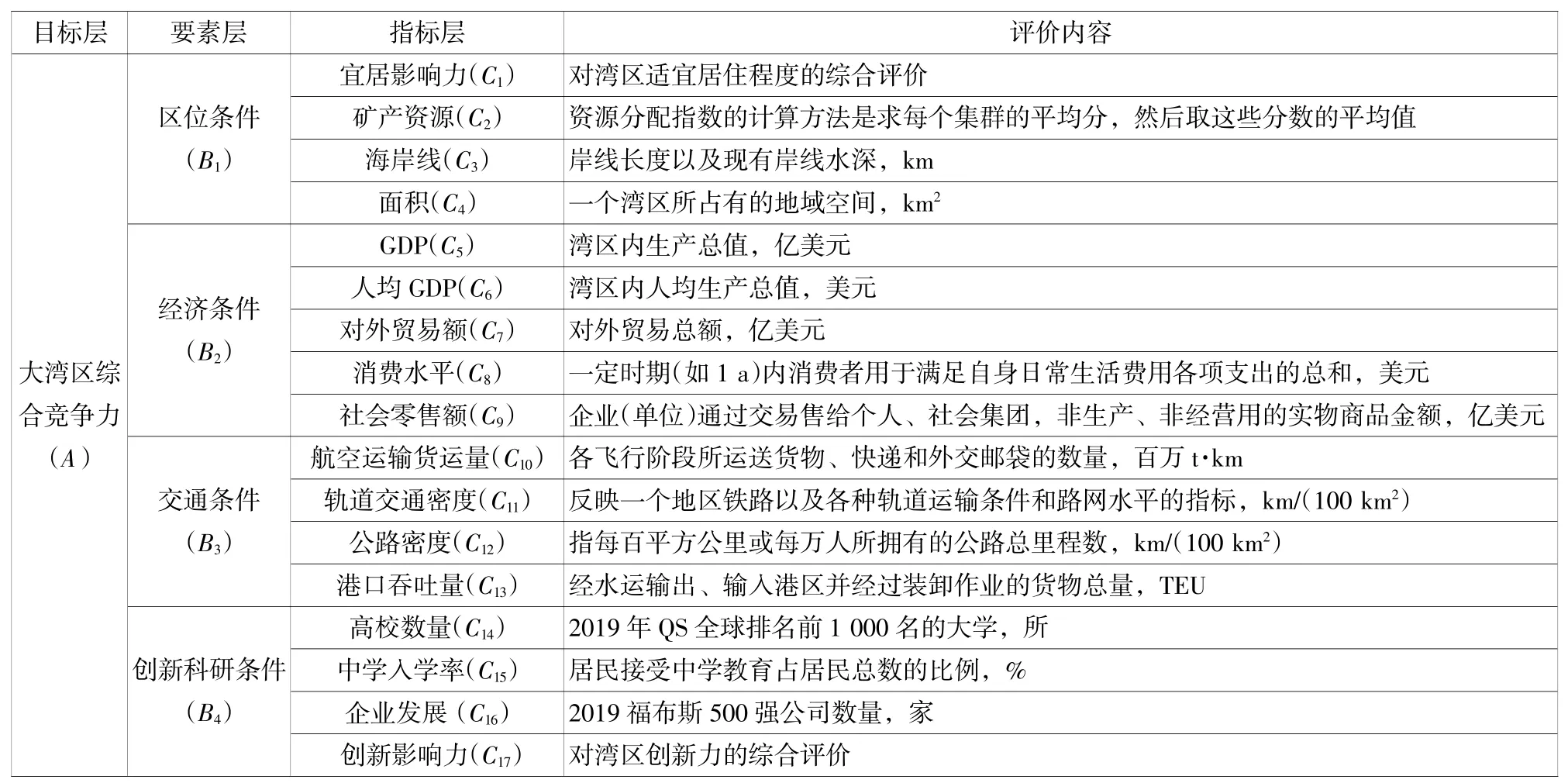
表1 大湾区综合竞争力评级指标体系Table 1 Comprehensive competitiveness rating index system of the Greater Bay Area

3 大湾区综合竞争力评价方法选择与模型构建

在竞争力研究的方法选择中，常用的评价方法有：层次分析法、综合模糊评价方法、因子分析法、灰色关联法等，每种方法均有其适用的范围。通过对各评价方法的优缺点分析，最终选择作灰色关联和模糊物元评价法相结合的方法作为大湾区综合竞争力的评价，该方法不仅能判断待评物元与标准物元之间的接近程度，还能弥补传统欧式算法计算关联系数的弊端。

3.1 基于灰色关联模糊物元法的评估模型

3.1.1 模糊物元法

根据文献[12]，模糊物元是以“事物”、“特征”、“模糊量值”组成的三元有序组R=（M，C，x）。其中m个事物组成的n维复合模糊物元R可记为：

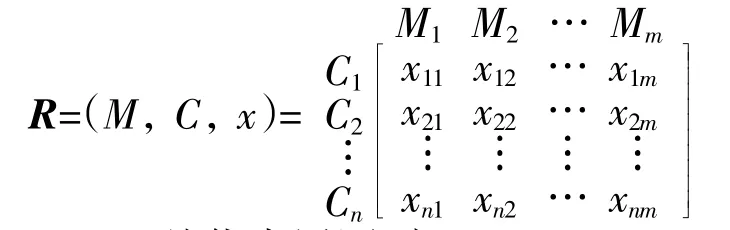
3.1.2 从优隶属原则

各单项指标相应的模糊值从属于标准方案各对应评价指标相应的模糊量值隶属程度，称为从优隶属度[12]。从指标对总体评价的影响来看，可将各指标分为两类，本文采用的是“效益型”指标，相应的属性越大越好，具体公式如下：

其中：max xij，min xij分别为每一个评价指标的最大值，最小值。由此可以得到从优隶属度模糊物元。

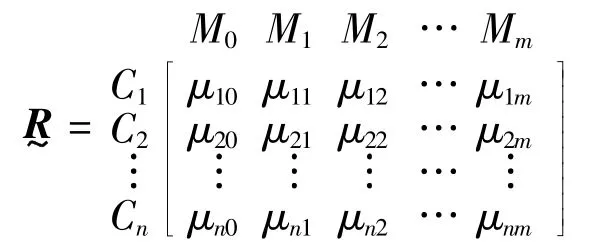
式中：为n维标准物元，μi0=1（i=1，2，…，n）。

3.1.3 确定指标权重

3.1.3 .1 AHP确定客观权重

1）建立结构层次模型，将评价的一级指标（要素层）和二级指标（指标层）的相关信息进行采集，构建层次分析模型，如表1所示。

2）构造判断矩阵，用成对比较法和1~9尺度，构造各层对上一层各因素的判断矩阵。

3）计算权向量并做一致性检验，对应于判断矩阵的最大特征值λmax和特征向量，计算的一致性指标CI和一致性比率CR，将特征向量经归一化后得到主观权重W。其中：式中：n为判断矩阵的阶数；RI为随机一致性指标。

3.1.3 .2变异系数法确定主观权重

1）求出各指标的平均值和标准差：

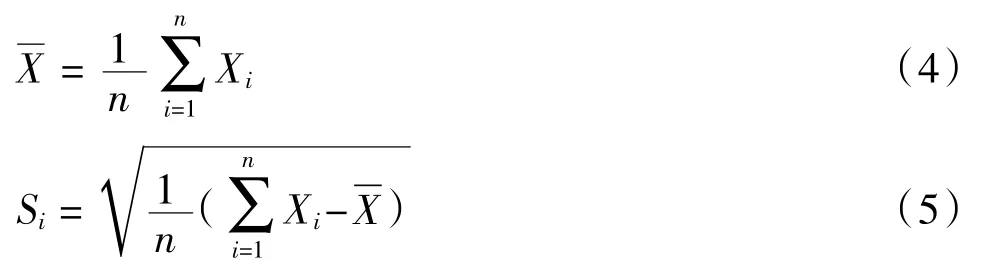
2）计算变异系数Zi：

3）计算各指标的权重Vi：

3.1.3 .3指标综合权重的确定权重

由以上AHP方法和变异系数法得到的主观权重向量W=（W1，W2，…，Wn）和客观权重向量V=（V1，V2，…，Vn），应用“乘法”集成法获取主客观综合权重系数ωi：

3.2 构造基于灰色关联分析的模糊物元分析模型

在利用模糊物元评定各物元优劣性时，大多数文献采用欧式距离作为关联数，具体算法如下：

为了充分考虑模糊物元和标准物元的“相近”程度，解决欧氏“贴近度”因仅考虑了待评样本向量终点与标准样本向量终点之间的距离而导致多个待评样本区分度不高的问题，本文将采用灰色关联和模糊物元相结合的方法进行计算。

3.2.1 计算关联系数

根据灰色系统理论，将标准物元M0={μ01，μ02，μ03，…，μ0n}作为参考数列，则Mj={μj1，μj2，μj3，…，μjn}与M0之间的关联系数计算公式为：

式中：ρ为分辩系数，ρ沂（0，1），一般取0.5。

3.2.2 计算关联度

计算关联度公式为：

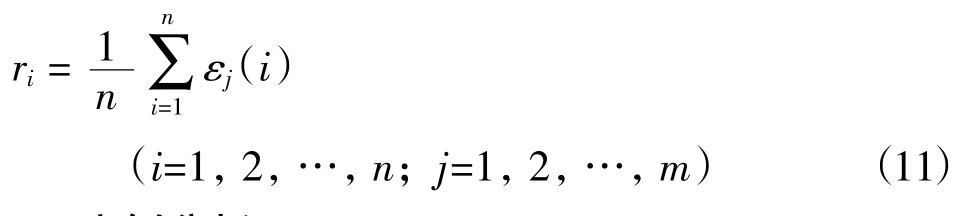
4 实例分析

4.1 指标值的确定

对于定性的指标本文采用问卷调查的形式获得，共调研了40位专家，获得37份有效问卷，最终整理的17项指标的原数据见表2（数据来源为世界银行、中国商务部、相关国家的商务部、统计局以及其他网络公开数据库）。

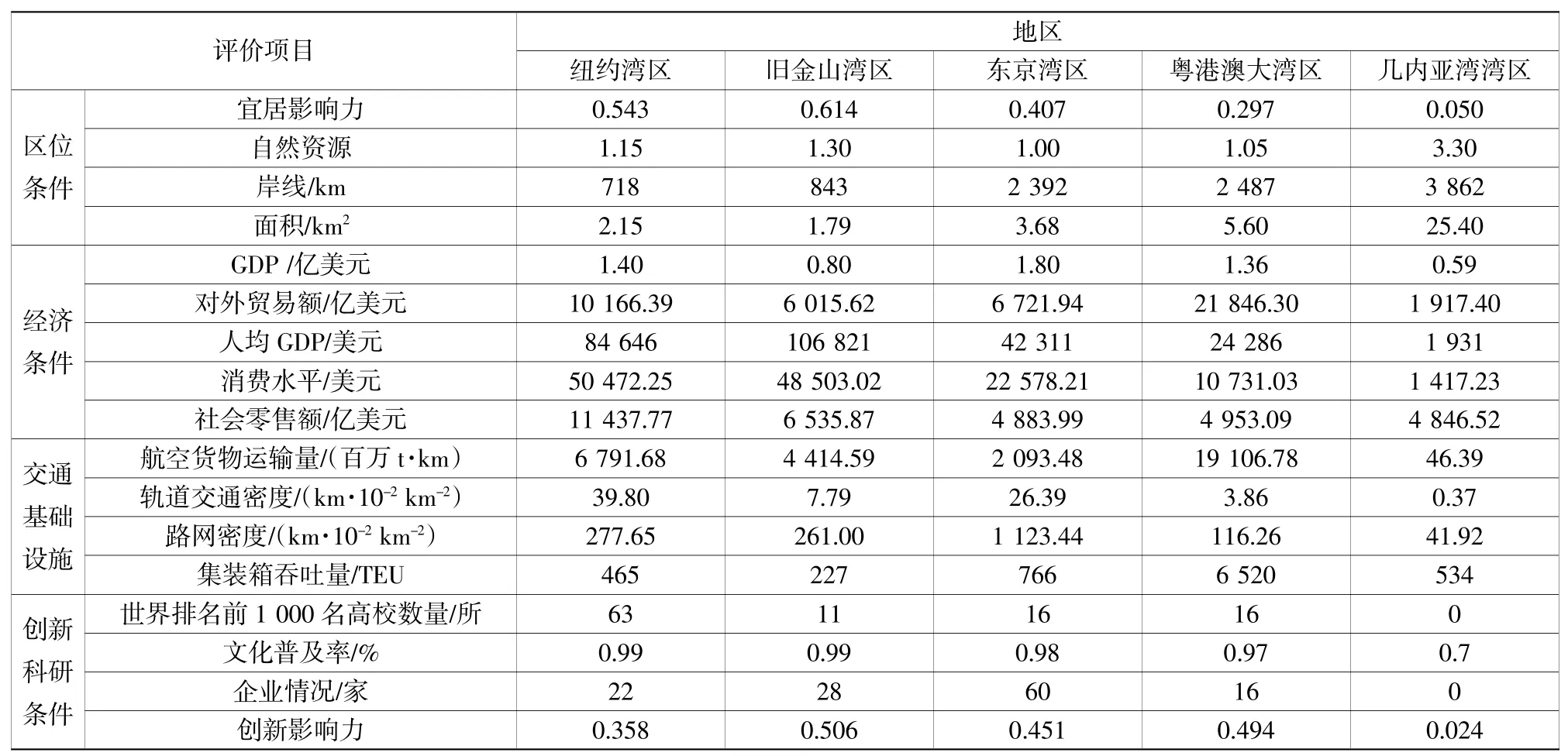
表2 五大湾区竞争力评价的灰色关联评价指标值Table 2 Grey relational evaluation index value for competitiveness evaluation of five bay areas

4.2 相关结论

利用公式（1），可以得到从优隶属度：

由于17项指标重要性不同，所以采用AHP法和变异系数法共同赋权，使结果更加准确，关联系数结果如表3所示。

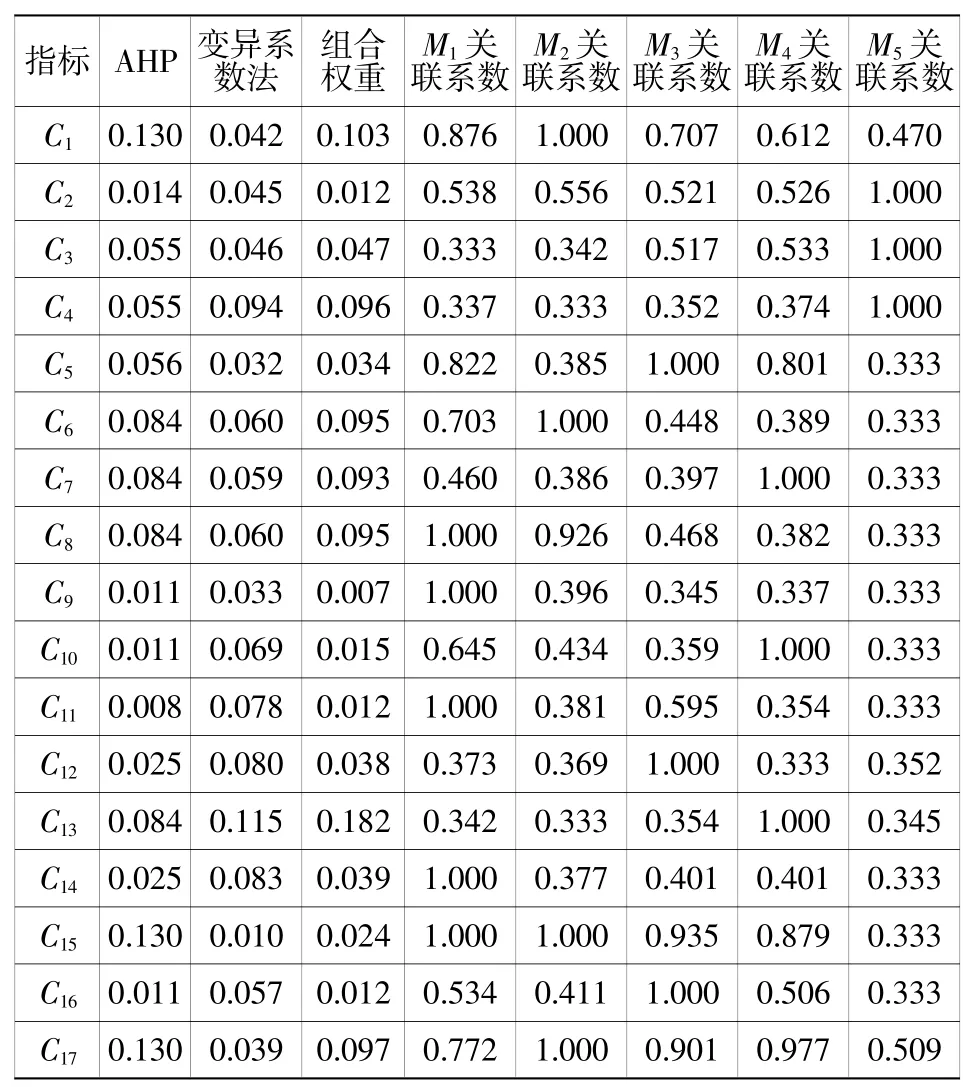
表3 指标权重与关联系数Table 3 Index weight and correlation coefficient

利用公式（11），得到五大湾区关联度见表4。

表4 关联度Table 4 Degrees of association

由评价结果可以得到，湾区排名依次是：纽约湾区，粤港澳大湾区，东京湾区，旧金山湾区，几内亚湾区，根据公式（9），计算得：ρH1=0.375，ρH2=0.308，ρH3=0.343，ρH4=0.440，ρH5=0.090，即排名依次是：粤港澳大湾区，纽约湾区，东京湾区，旧金山湾区，几内亚湾区。纽约湾区虽然有4个系数小于0.400，但是所占比例都较小，且在17项指标中有4项指标最高，位于五大湾区之首，所占比重都较高。

5 结语

本文基于对大湾区的影响因素进行分析，构建了几内亚湾区竞争力评价体系，并通过灰色关联和模糊物元相结合的方法对世界现有的四大湾区和几内亚湾区进行了评价和排序，并通过欧式“贴近度”对结论进行了进一步验证，结果显示，纽约湾区位于五大湾区之首，几内亚湾区最末。

运用AHP和变异系数法计算量化各指标权重，结果显示，几内亚湾区在资源、自然环境的破坏程度等方面占有绝对的优势，但是其他各个方面得分均较低，受基础设施建设、经济基础和创新环境等方面等权重系数较大的指标影响，无法将其在资源与自然环境方面的优势发挥出来，较为落后。亟需从实现工业化转型、加强技术升级和创新、完善交通基础设施和重视教育发展、培养专业人才等方面补足短板，填补相关领域知识和技术缺口等来提高区域竞争力。

湾区的建设是一个长期且复杂的过程，湾区竞争力又是一个相当广泛的概念，本文的评价体系还不够涵盖湾区评价的全部内容，如何使得评价指标体系更加完善科学标准，需要结合在后期的实践中进一步研究和改进。