混凝土面板堆石坝施工后变形数值模拟
2021-04-27江亨锦
江亨锦
(福建省永定区水利水电工程质量监督站,福建 永定 364100)
1 概 述
混凝土面板堆石坝的施工后变形由多种因素引起,如水库地下水位的反复变化、渗流驱动的内部侵蚀过程、地震以及堆石材料的风化。导致固体硬度下降,并导致晶粒破碎和流变变形。不同的环境条件下,风化作用可以复杂的方式启动,并对长期变形产生强烈影响。对于堆石坝材料,含水量的变化会导致固体硬度的加速退化。变形主要与面板堆石坝材料的风化状态、压实度、坝基地质条件、坝体渗漏特性、局部缺陷及其他施工细节有关。
混凝土面板堆石坝的长期变形预测是一项具有挑战性的任务。在这种情况下,选择合适的本构模型和精确校准所涉及的常数对计算结果的质量至关重要。根据堆石材料的类型,本文提出数值模拟的本构关系。
2 工程概况
下黄水库坝址位于福建省永定区湖坑镇北部附近金丰溪右岸一级支流五黄溪中游,坝址以上流域面积8.46 km2,河长4.02 km,坡降39%。下黄水库坝型为C25砼面板堆石坝,最大坝高31.5 m。根据《防洪标准》(GB 50201-2014),本工程为Ⅳ等工程,工程规模为小(Ⅰ)型,大坝为4级建筑物,导流等临时建筑物为5级建筑物。本工程水库大坝为C25砼面板堆石坝,根据《防洪标准》(GB 50201-2014),大坝设计洪水重现期为30年,校核洪水重现期为300年。相应设计洪水位为432.11 m,校核洪水位为433.16 m,水库正常蓄水位430.00 m。大坝高程434.50 m,河床建基面最低高程403.00 m,最大坝高31.5 m,坝顶长83 m,坝顶宽5.0 m。挡水坝基本剖面图为三角形,见图1。
本文主要研究蓄水和堆石材料蠕变引起的面板堆石坝施工后变形的数值模拟。为此,考虑高度为31.5 m的人工混凝土面板堆石坝。大坝上下游坡比均为1∶1.5,蓄水后上游水位为27 m。坝体由主堆石区、过渡层区、混凝土板和混凝土趾板组成,板底厚1.0 m。
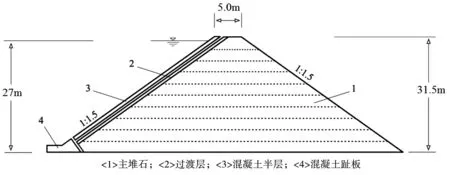
图1 面板堆石坝横断面示意图
对于面板堆石坝长期变形的数值模拟,采用亚塑性本构模型。在该模型中,引入固体硬度来反映材料的风化状态对其刚度的影响。在这个意义上,颗粒的硬度与颗粒的硬度无关。在该模型中,长期变形与固体硬度的退化有关。因此,除亚塑性本构方程外,还需要一个用于模拟固体硬度退化的附加演化方程。
3 数值模型与本构参数
采用ABAQUS有限元模拟。图1所示的混凝土面板堆石坝由4 841个平面应变条件下的双线性四边形单元组成。假定坝基是刚性的和不可移动的,因此沿坝体底面的单元节点是固定的。利用ABAQUS提供的接触概念,模拟混凝土板与过渡层之间,以及混凝土趾板(柱脚)、混凝土板、过渡层和堆石料之间的界面行为。对于施工后变形的模拟,应考虑以下步骤:
第1步:模拟10层同高堆石坝施工的影响,得到重力荷载作用下堆石料的初始应力分布。在此步骤中,仅激活<1>的主要堆石材料和<4>的柱基。
第2步:混凝土板<3>和过渡层<2>相对于这两种材料和柱基之间的界面被激活。为了研究施工后的性能,将混凝土面板堆石坝施工引起的变形设置为零。
第3步:计算蓄水引起的变形。
第4步:模拟主要堆石材料<1>和过渡层<2>刚度退化导致的长期变形。
混凝土板和基座的材料性能描述为线弹性材料,弹性模量为E=20 GPa,泊松比为v=0.17,密度为ρ=2 400 kg/m3。本构模型包括10个参数,见表1,分别为固体硬度Hs0、风化后的固体硬度hsw、临界摩擦角φc、临界孔隙比ec、最大孔隙比ei、最小孔隙比ed、刚度系数fs,这里α和β是材料常数。对于压实填石材料,初始孔隙比e0=0.33,密度ρ=2 200 kg/m3在所有计算中都被考虑在内。

表1 3种不同堆石料的本构参数
4 数值结果分析
使用本构参数集A获得的数值结果见图2-图4。具体而言,蓄水后的垂直位移等值线和相应的孔隙比变化见图2(a)和图3(a)。虽然附加压实主要集中在大坝上游部分,但下游部分的变形几乎为零。特别是在混凝土板的半高处,垂直位移达到极值,最大压实度出现在坝趾附近。由于固体硬度的降低,整个堆石坝发生了蠕变沉降。额外的压实可以解释为颗粒破碎和颗粒重新定向到更密集的状态。图2(b)和图3(b)为蓄水和15年后固体硬度下降所产生的数量。显然,在假定的固体硬度退化参数下,相应的长期变形比蓄水引起的变形更明显。
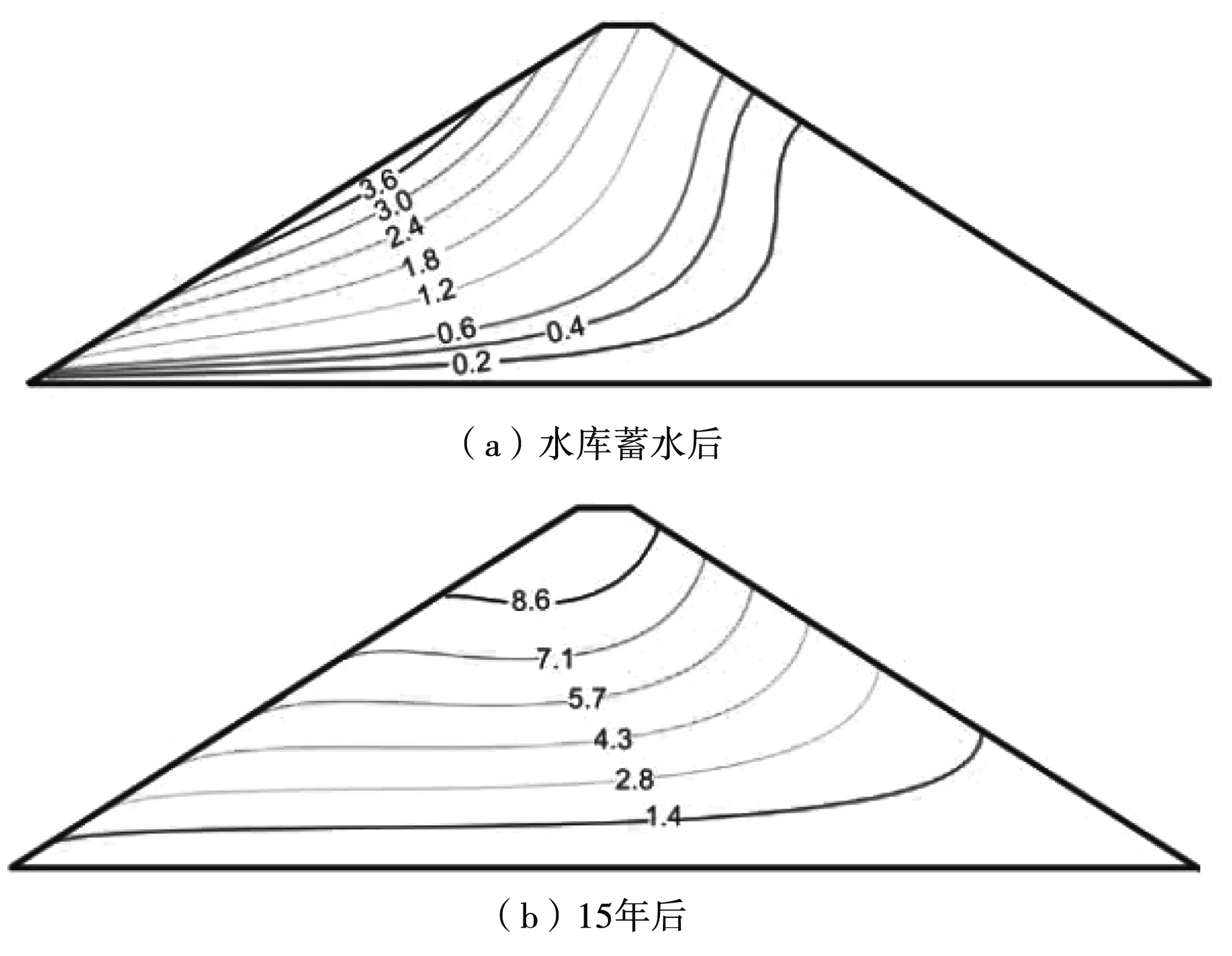
图2 垂直位移等值线(单位:cm)

图3 孔隙比降低曲线
图4为水库蓄水后(曲线2)、第一年年末(曲线3)、2年后(曲线4)和3年后(曲线5)混凝土板的正常挠度。虽然水压力随着深度的增加而增大,但蓄水后混凝土板的上下挠度基本相同。最大挠度出现在靠近中心的位置,这与图3(a)所示堆石材料的垂直位移分布类似。但长期变形会导致顶部混凝土板的挠度单调增加。

图4 混凝土板的正常挠度
本文主要模拟堆石料力学特性的主要本构关系。该模型统一反映了压力和密度对增量刚度、峰值摩擦角和体积应变行为的影响,以及固体硬度下降对蠕变和应力松弛的影响。引入数值模型以及本构参数,特别是对大坝蓄水后的变形和大坝建成后3年内的蠕变演变进行了有限元计算。对数值模拟结果进行讨论,并与监测数据进行比较,结果见图5。
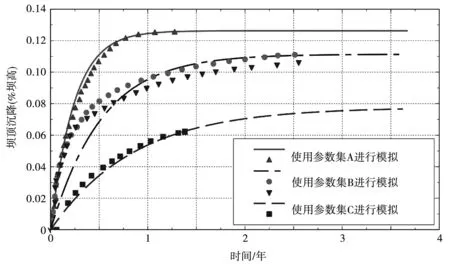
图5 蓄水后3年内坝顶沉降的演变
蓄水后3年内坝顶沉降的演变见图5,将数值模拟与4个混凝土面板堆石坝的监测数据进行比较。结果表明,在本模型下,蠕变变形量主要取决于最终的、渐近的固体硬度值与初始值之间的差值(即hsw-hs0),而蠕变变形速度与固体硬度速率有关。在这种情况下,应注意的是,既没有考虑相关三维几何结构的影响,也没有考虑不同堆石类型和粒度分布的个别特性,这当然是精确校准所必需的。因此,本研究只应证明目前的低塑性本构模型能够模拟长期变形。
5 结 论
采用亚塑性本构模型研究了面板堆石坝施工后变形,该模型适用于描述堆石坝材料的流变特性。模拟蠕变和应力松弛等流变特性的关键参数是固体硬度状态及其速率。在连续介质描述的意义下,这些量被引入本构模型中。固体硬度的变化会导致蠕变变形和/或应力松弛。对于堆石材料的数值模拟,使用的本构参数与风化花岗岩相关。计算结果表明,与3年后的长期变形相比,混凝土板顶部的瞬时法向挠度较小,对于计算的坝顶沉降也可以得出同样的结论。计算的坝顶沉降量与4个混凝土面板堆石坝监测数据的比较表明,坝顶沉降量取决于固体硬度的最终渐近值之差,而蠕变变形速度与固体硬度的速率有关。
