温室推拉门组合式门边柱设计方法
2021-04-27
承建温室工程的过程中经常会遇到要求加大推拉门尺寸的情况,以方便一些大型车辆的出入,而且要求用铝合金推拉门。例如有温室案例要求推拉门尺寸为宽× 高=4 m×3.2 m,每扇门如图1。为保证推拉门能够承受10 级风(W0=0.40 kPa),首先需要考虑是否有专用门边柱铝型材。在未找到合适专用门边柱铝型材的情况下,不得不采用普通铝合金矩形管来代替。青岛蓝天温室有限公司选择尺寸为120 mm×60 mm×1.2 mm 的6063-T5 铝合金型材,然后在铝管内插入镀锌板折成的槽钢(图2),用一种组合结构的门边柱来解决此问题,其横截面如图3。
该组合结构门边柱需通过计算来明确镀锌板槽钢的截面尺寸。冷弯槽钢用镀锌板(Q235)制作,其屈服点σs=215 MPa。设风荷载垂直作用在每扇门上,最终由各门扇的两个边柱承载。每扇门在上下导轨间靠滑轮左右移动,每个门边柱受力情况视为一简支梁(图4),受力弯矩见图5。
假设风荷载垂直作用在门上,且风荷载为均布荷载,按照GB/T51183-2016《农业温室结构荷载规范》基本风压W0=0.40 kN/m2,则有:

图1 推拉门/mm

图2 冷弯槽钢/mm
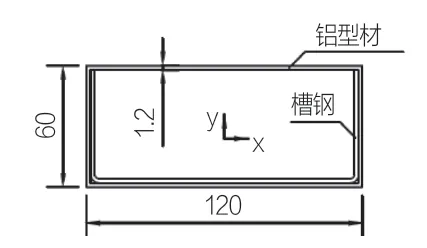
图3 门边柱截面/mm

图4 门边柱受力图/mm

图5 门边柱受力弯矩图/mm
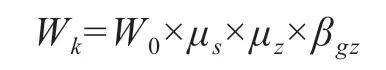
式中:Wk—风荷载标准值,kN/m2;
W0—基本风压,kN/m2,W0=0.40 kN/m2;
μs—局部风压体型系数,μs=1.2。
μz—风压高度变化系数,μz=1
βgz—阵风系数,βgz=1.7
代入得:
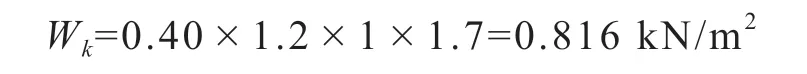
每扇门受风荷载:

式中:A—单扇门面积,m2,A=3.2×2=6.4 m2。
代入得:
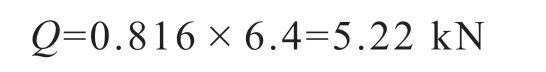
单个门边柱受的均布荷载:
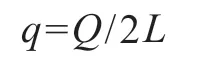
式中:L—门边柱上下支点间距离,m,L=3.2 m。
代入得:

所有符合此数值地区均可使用此设计,假设组合式门边柱在风荷载作用下,其铝合金矩形管与镀锌板槽钢是同时起作用的,即它们所产生的挠度是相等的:
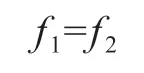
式中:f1—铝合金矩形管在风荷载下的最大挠度,mm;
f2—镀锌板槽钢在风荷载下的最大挠度,mm。
铝合金门边柱在风荷载作用下最大挠度规定为≤20 mm[1]。
用简支梁在均布荷载下求挠度的公式可求出每个门边柱的最大挠度:

式中:fmax—门边柱在风荷载下的最大挠度,cm,fmax=2 cm。
得:
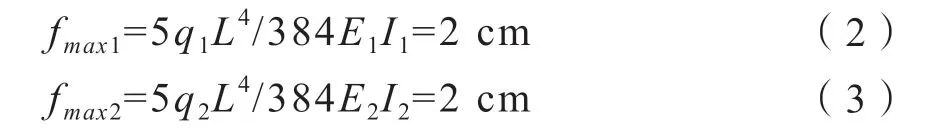
式中:q1、q2—分别为铝合金矩形管与镀锌板槽钢所受到的风荷载之均布荷载,kN/m;
E1、E2—分别为铝合金矩形管与镀锌板槽钢的材料弹性模量,MPa,E1=0.7×105MPa、E2=2×105MPa;
I1、I2—分别为铝合金矩形管与镀锌板槽钢的截面轴惯性矩,cm4,I1=28.72 cm4;
代入(2)得:

因为q1+q2=q
得出q2=q-q1
将q2值代入(3)得:
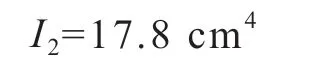
由于镀锌板槽钢截面的外形尺寸受铝合金矩形管内腔尺寸所限,所以仅需决定其壁厚即可。通过试算,当壁厚为2.5 mm 时,其截面轴惯性矩I2=18.6 cm4,大于初设计算值17.8 cm4,这样,组合式截面二种材料承担的均布荷载就会发生变化,而必须进行修正。
通过式(2)与(3),可得:
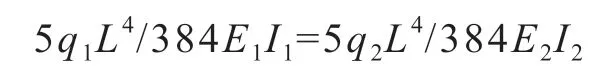
简化得:
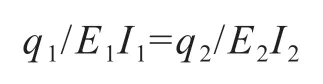
因此得出q1=q2E1I1/E2I2=(q-q1)E1I1/E2I2
此处的I2为实际应用镀锌板槽钢的截面轴惯性矩。
代入各值得:

由于实际应用槽钢的截面轴惯性矩增大,因此在额定风荷载下其最大挠度会发生减小。
将选用镀锌板槽钢的截面轴惯性矩和重新分配的均布荷载值代入式(1)得:
fmax1=fmax2=19.4 mm ≤20 mm,符合规定。
对于所选铝合金矩形管及镀锌板槽钢,虽然满足挠度要求,但还应进行机械强度方面的验证。对于均布荷载下的简支梁,最大弯矩发生在梁之中部,如图5 所示。根据其最大弯矩的计算公式:
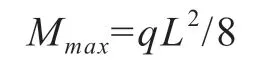
式中:Mmax—边柱组件在风荷载下的最大弯矩,kN·m。
代入各已知数值,得:

依据公式:

式中:Wx—边柱组件的截面系数,cm3,Wx1=9.57 cm3、Wx2=4.4 cm3;
σmax—组合式门边柱型材最大弯矩处的截面应力,N/mm2。
代入即得组合门边柱型材最大弯矩处的截面应力:

门边柱计算应力应符合下式要求:
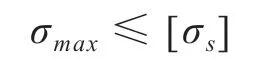
式中:[σs]—材料强度标准值,N/mm2;
其中:
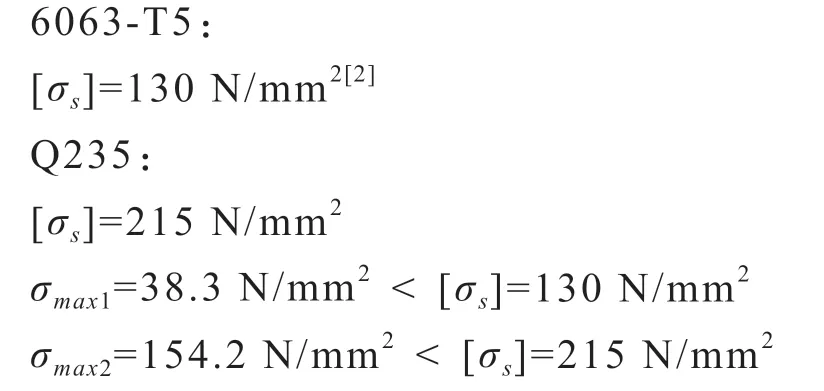
经过计算,各数据均满足强度要求。
