竖直圆管内冲击射流过程中流体运动现象的数值计算

杨 柳，张 爽，王 倩

竖直圆管内冲击射流过程中流体运动现象的数值计算

杨 柳1，张 爽2，王 倩3

（1.锦州天宇电炉有限公司，辽宁 锦州 121011；2.中冶京诚工程技术有限公司，北京 100176；3.锦州七七七微电子有限责任公司，辽宁 锦州 121000）

利用计算流体动力学方法对竖直圆管内的冲击射流过程进行深入研究。为了提高计算结果的精准性，计算过程选用SST湍流模型。利用气体压力损失的理论计算值验证数学模型的准确性。计算结果表明，当入射气体的流速增加时，入射气体在竖直圆管内部的流速呈现“阶梯式”衰减；气体沿冲击射流方向上，流速呈非线性衰减，突变的“临界点”位于喷嘴与外管间距的1/2～5/6处，湍动能峰值位置则集中出现在1/4～1/3处；入射气体依次经过各个喷嘴时，气体在各喷嘴中心平面径向上的速度分布由“中心峰值”逐渐转变为“壁面峰值”。

冲击；射流；SST湍流模型；湍流；边界层

冲击射流主要是流体在压差作用下通过一个圆形或狭缝形喷嘴垂直(或呈一定倾角)地喷射到冷却工件的表面上，从而使直接受到冲击的区域产生很强的换热效果[1]，以此满足工件的某种性能、工艺要求或达到强烈换热的目的。

冲击射流出口的流速是近似均匀的，射流离开喷嘴表面后，射流的直径不断扩大，整个截面上速度逐渐呈现中间大，逐渐向边缘减小的不均匀状态，当射流抵达被冲击物体的壁面后，流体向四周沿壁面扩散。

随着科技日新月异的快速发展和工业化进程的不断加快，冲击射流已经广泛应用于材料、机械、航天、化工、电子等重点行业和关键领域，同时冲击射流也成为国内外学者研究的重要课题，并取得了丰硕的成果[2-10]。

Jambunathan等[7]通过不同实验数据的对比，明确阐述了流动条件、几何形状以及湍流参数等流体状态参数对冲击射流过程中传热过程的影响。陈翼等[9]利用计算流体动力学软件，采用K-epsilon和RNG K-epsilon模型，计算不同位置的气体浓度分布，并结合实验结果对比和分析，研究结果说明计算气体混合扩散过程的数学模型真实可靠，并成功预测速度场和浓度场的分布，为射流混合器的设计提供理论依据。徐亮等[10]分别采用实验和数值模拟方法研究喷嘴形状和流体旋度对冲击射流压力损失和传热特性的影响，研究结果显示，不同喷嘴形状对应的换热效果主要取决于流体的Reynolds数和旋度的综合效应，流体的旋流越强，旋度越大，压力损失相对较小，换热的Nusselt数峰值越小，换热效果更佳均匀。

本文以竖直圆管内冲击射流过程中流体的运动现象为研究对象，重点研究冲击射流过程中流体的压力损失、流速分布以及湍动能分布特性，探求冲击射流过程中流体的流动特性，掌握其流动规律，为进一步研究传热、传质传输过程提供理论依据。

1 数学模型

1.1 控制方程

本文认定冲击射流过程中流体介质为牛顿流体，因此在冲击射流过程中，流体满足如下连续性方程和动量方程[11]：

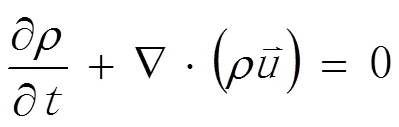
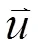
1.2 基本假设

仅研究圆管内流体的流动现象，忽略因辐射和对流传热现象对流动现象的影响。

不考虑温度变化对流体及流动现象的影响。

内外管壁均为光滑壁面。

1.3 几何模型及网格化

本研究的几何模型尺寸参见表1。经网格无关性检查与验证，最终确定网格数量为198 920，且全部为六面体网格。几何模型和网格化示意图可参见图1和图2。

表1 几何模型尺寸

外管管径/mm内管管径/mm管长度/mm内管壁厚/mm狭缝喷嘴宽度/mm狭缝喷嘴数量 10040350/350225

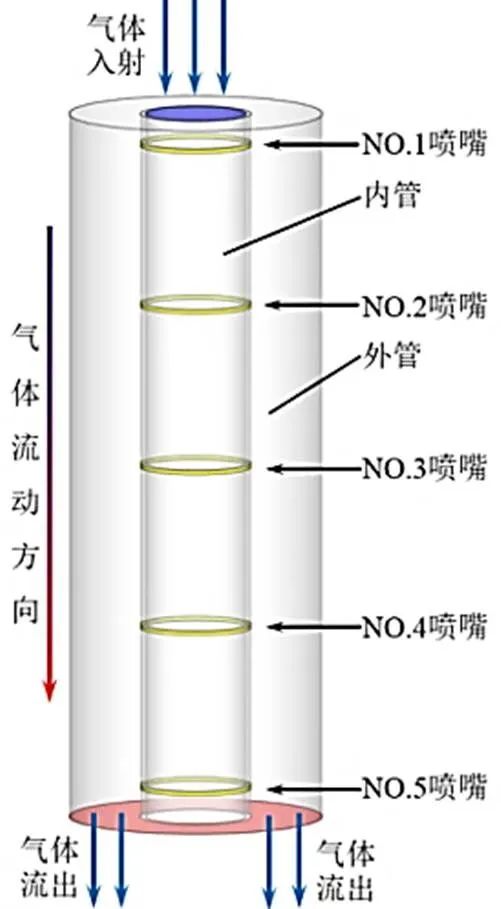
图1 几何模型

图2 几何模型网格化

1.4 流体的物性参数及数学模型的边界条件

流体的物性参数参见表2。数学模型采用速度条件作为入口条件；出口则采用敞口条件，相对压力为0；壁面条件是内管和外管壁都是光滑的，且选用不滑移条件。

表2 流体的物性参数

流体介质温度/K密度/(kg·m-3)动力粘度/(Pa·s) 空气3001.18518.31×10-6

1.5 湍流模型

一般来说，K-epsilon湍流模型是针对湍流发展非常充分的湍流流动来建立的，换言之，它是针对高Reynolds数的湍流计算模型，然而当Reynolds数较低时，湍流的脉动影响不如粘性力的影响大，粘性力在壁面附近区域对流体流动的影响不可忽视，K-epsilon湍流模型的计算结果与真实值之间偏差较大，这一点已经得到了证实[12]。Shear Stress Transport湍流模型(又称SST湍流模型)适用于壁面附近区域的湍流剪切力计算，可以有效提高结果的准确性，这一点已经被证实[13-14]。因此，为了提高近壁面区域计算的精准性，本文选用Shear Stress Transport湍流模型。

2 计算结果分析与讨论

2.1 计算结果验证

冲击射流过程中气体的压力损失主要是由流体微团相互碰撞，在流体中产生漩涡或摩擦，造成能量不断损失和耗散，这种压力损失主要发生在流动状态急剧变化的急变流中。利用数值模拟计算压力损失与理论公式计算结果进行对比，如图3所示。

图3 理论计算值与数值模拟计算结果对比

图3显示数值模拟的计算结果和理论公式计算值总体趋势是一致的，且误差在允许的范围之内，验证了数学模型的可信度。由此可知，当气体入射速度由8 m/s增加至14 m/s时，压力损失由93 Pa增加至287 Pa，压力损失随入射气体流速的增加而增加。

2.2 内管内部气体流动速度分布

图4表示当气体的入射速度分别为8.0、9.5、11.0、12.5、14.0 m/s时，内管内部沿中心轴线上速度的分布情况。总体而言，内管内部的气体流速呈现“阶梯状”下降趋势，即射流气体依次经过喷嘴后，气体的流速呈现逐级递减的趋势，其流速变化位置与喷嘴位置大体相同。在喷嘴之间，由于气体流量相同，截面积相同，因此流速几乎无任何变化，当临近喷嘴时，部分气体经喷嘴射出，气体流量下降，因而流速降低，直至流速为零。随着气体入射速度的增加，气体在管内的流速明显增加，但射流速度的增加，也使得气体流速的下降率随之增加，即气体的入射速度越大，气体在内管内中心轴线上的流速下降率越明显。

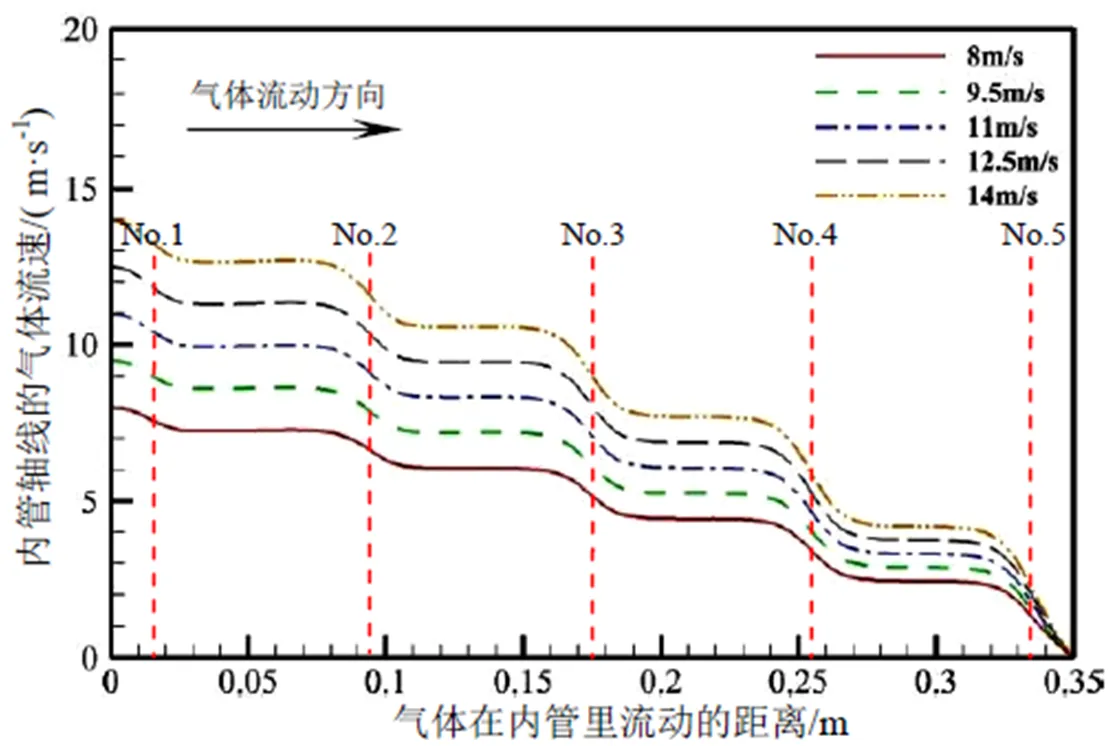
图4 内管内部沿中心轴线方向速度分布

气体在内管内部中心轴线上的流动过程中，气体流速变化呈现“阶梯状”下降趋势，在内管内部临近喷嘴附近的轴线方向上，气体流速的变化呈现相同的趋势，仅在临近喷嘴位置时，流速变化差异很大。气体沿中心轴线向下流动，临近喷嘴位置时，流速呈现相对缓慢下降趋势，而沿临近喷嘴附近的轴线向下流动，临近喷嘴位置时，流速先形成一个上峰值，而后形成“断崖式”下降率，在刚经过喷嘴位置后，形成一个下峰值，而后快速趋于平缓，气体流速基本无变化。气体在内管内部流动，依次经过各个喷嘴时，其规律基本相同，如图5所示。

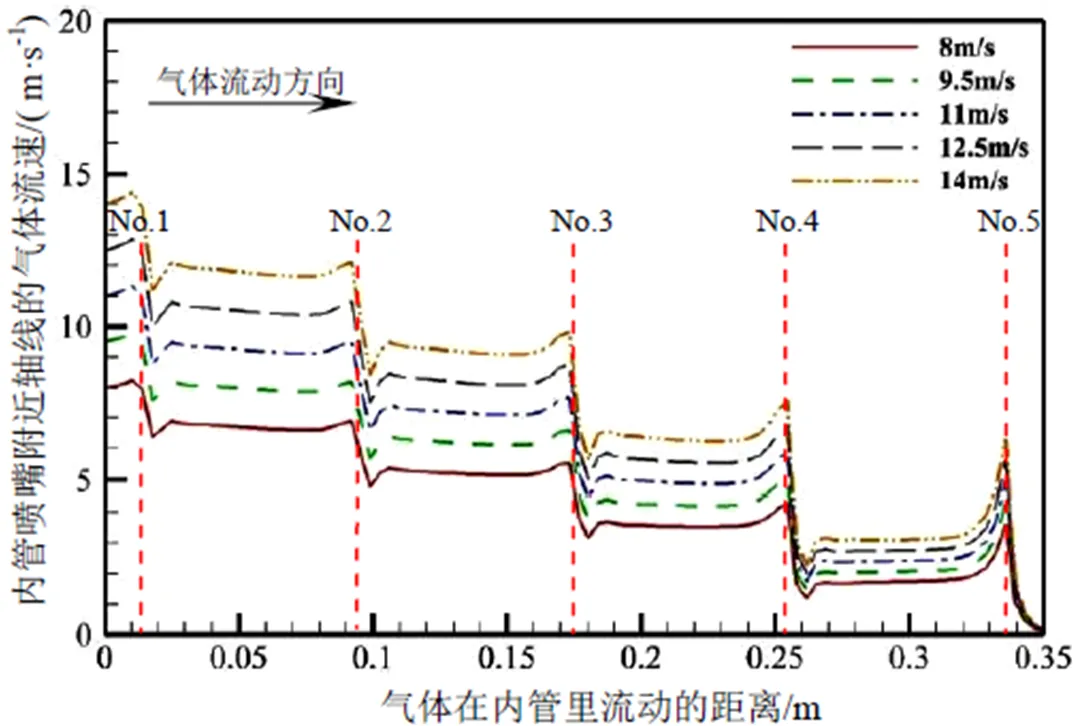
图5 内管内部沿喷嘴附近轴线方向速度分布

这一现象主要是由于气体流动过程中，当临近喷嘴时，在喷嘴周围区域产生压差，宏观上则体现为对内管内部气体产生引流、卷吸作用，使冲击射流的流速快速提高，并且在此作用下，内管内部的气体流速快速下降，因此形成“断崖式”下降率，而后快速趋于平缓。随着气体依次经过喷嘴后，内管内部的气体流量依次减少，气体流速逐渐降低，内管外部的气体流量依次增加，外部气体流量增加，因此压差增加，引流、卷吸作用进一步增强，因此使其对内管内部临近喷嘴位置的气体抽吸能力增强。正如图6所展示的，随着气体在圆管内部流速的逐渐降低，其上峰值和“断崖式”下降率越发明显。

2.3 冲击射流过程中气体速度及湍动能分布

通过图6可以分析，气体在外管内部冲击射流过程中，气体入射速度对气体射流速度分布的影响。通过图6中5幅流速变化曲线分布图的对比可以看出，入射气体依次经过No.1~No.5狭缝喷嘴后，气体脱离狭缝喷嘴时的流速明显增加，并且在外管内湍流冲击射流过程中，气体射流流速亦随之增加；而且当气体自狭缝喷嘴脱离后，射流气体会受到其他喷嘴喷出的气体的挤压、卷吸、流体微团的相互碰撞，粘性力等相互作用，此过程中能量不断损失和耗散，因此，射流气体的流速呈逐渐衰减的现象，且这种衰减是非线性的。总结图6中5幅气体流速分布图可知，当气体脱离狭缝喷嘴后，气体射流速度衰减较快，直至喷嘴与外管间距的1/2~5/6时，气体射流速度的衰减速率出现“临界点”，而后，气体射流速度衰减逐渐减缓，甚至开始呈现缓慢增加的趋势。显然，在临界点前，流速的变化是由于靠近内管外壁侧的气体竖直向下运动过程中，对射流气体的挤压、碰撞而引起的；在临界点后，流速的变化则是由于临近外管内壁侧气体的粘性力起主导作用而产生的。

图6 不同喷嘴位置冲击过程中气体速度的分布

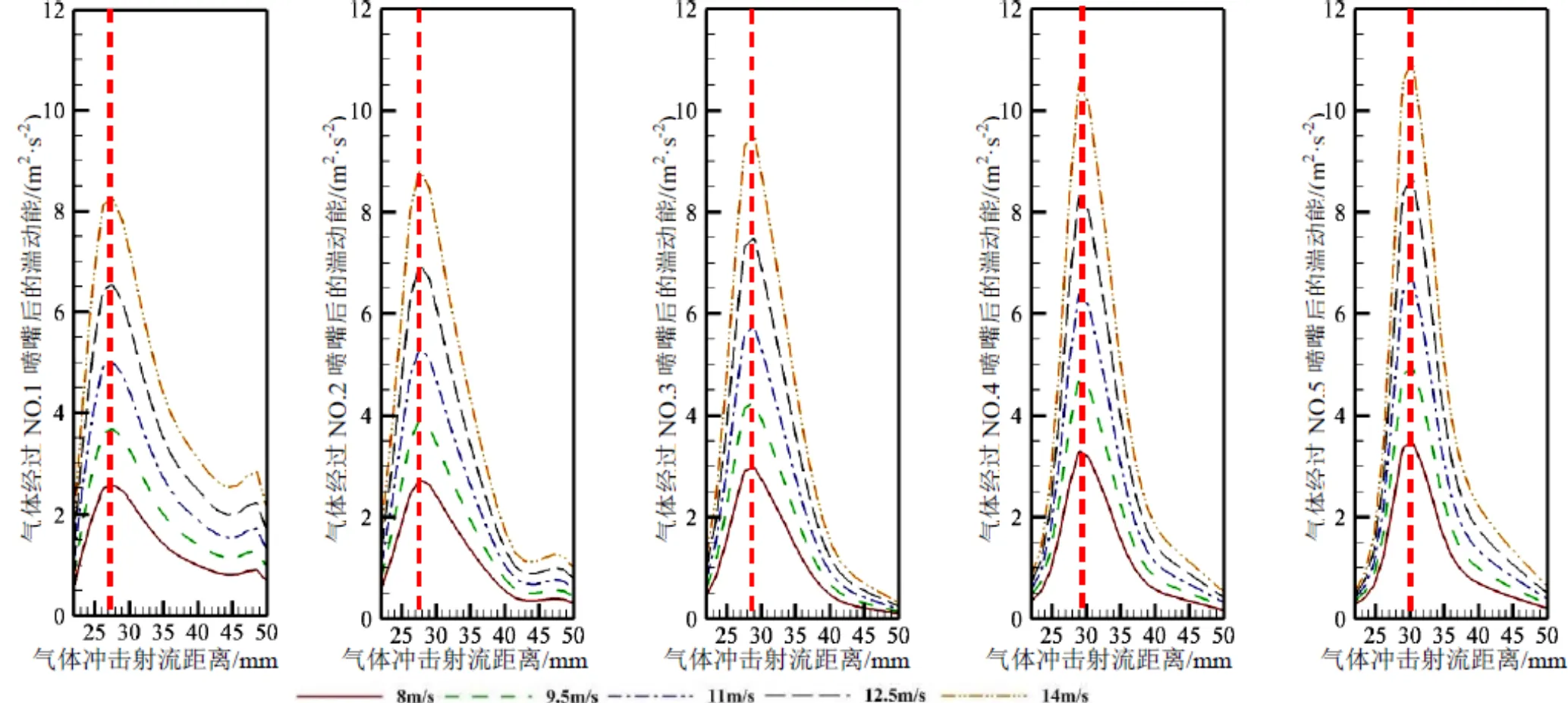
图7 不同喷嘴位置冲击过程中气体湍动能的分布

当气体的入射流速依次为8.0、9.5、11.0、12.5、14.0 m/s时，气体在内管和外管之间完成冲击射流过程中，气体的湍动能变化呈现先增加后下降的趋势，且随着气体射流流速的增加，湍动能变化越发明显；随着气体依次经过各个喷嘴，湍动能显现逐渐增加的现象。虽然气体的流速增加，但气体在冲击射流过程中的湍动能峰值位置集中出现在1/4～1/3处，如图7所示。

2.4 各喷嘴中心平面径向上气体速度分布

图8表明了气体进入内管，依次通过各个狭缝喷嘴No.1~No.5后，在外管内部形成冲击射流过程中，气体在各喷嘴中心平面径向上流速分布的情况。通过图8的5幅流速曲线分布图对比可以发现：入射气体完成流动过程中，在狭缝喷嘴No.1中心平面径向上形成“中心峰值”，即气体的峰值流速出现在内管内部的中心位置，流速向外管内壁面处逐渐递减，并呈轴对称分布；随着入射气体依次经过各个狭缝喷嘴后，气体在喷嘴中心平面径向上的“中心峰值”逐渐减弱，在内管内部的流速分布趋于平缓，且逐渐形成“壁面峰值”，即气体的峰值流速出现在狭缝喷嘴附近，而气体的最低流速则出现在内管内部中心位置，并呈轴对称分布。另外，随着气体入射速度的增加，气体在各喷嘴中心平面径向上形成“中心峰值”和“壁面峰值”越发显著。这也说明了在内管内部，气体流量逐渐减少，相同截面积的情况下，气体的流速逐渐降低，而在内管外部，气体的流量增加，对气体的卷吸和引流作用增强，进而将冲击射流的气体流速提高。

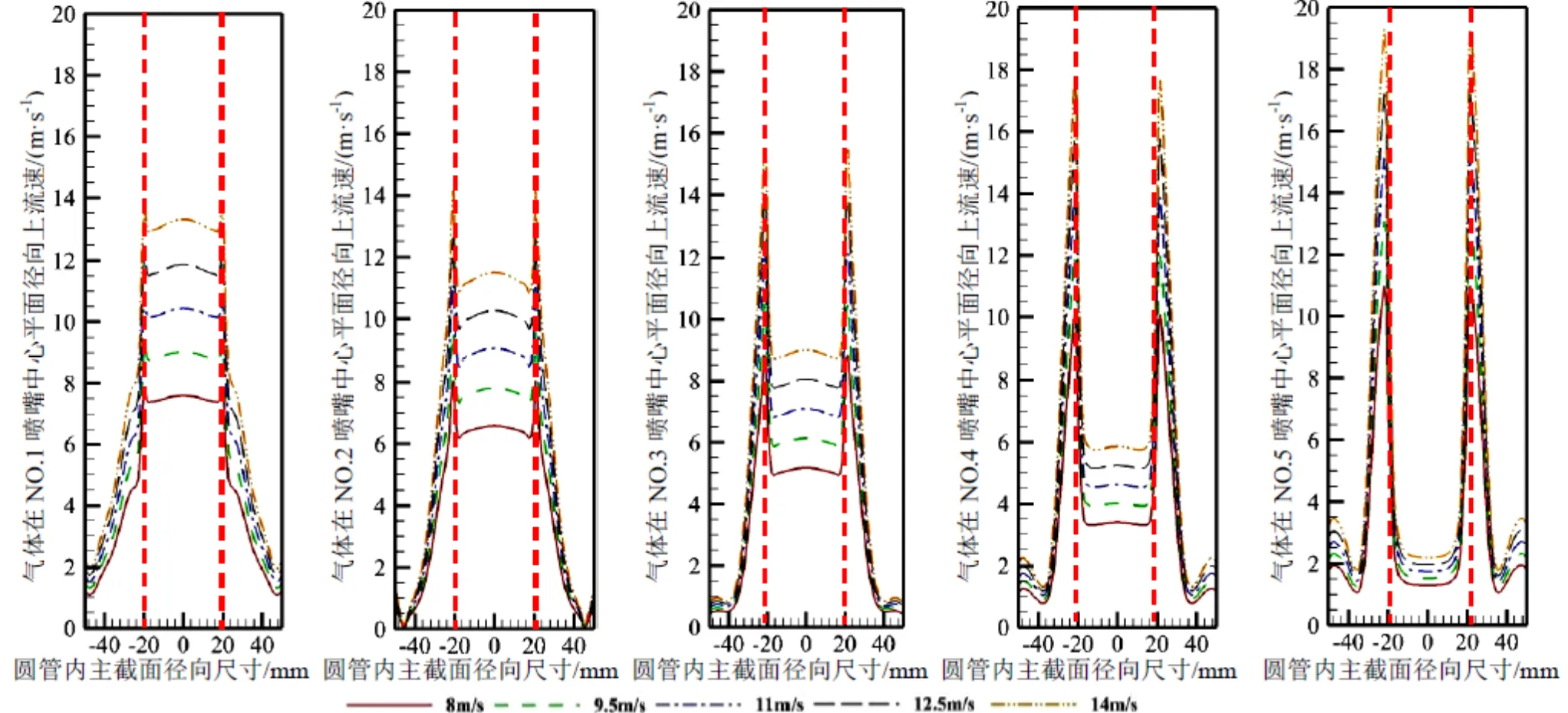
图8 喷嘴中心平面径向上气体的速度分布

2.5 气体入射速度对低速流动区面积的影响

本文认定，当气体流动区域内的流速≤0.4 m/s时，此流动区域被认定为低速流动区域(死区)。一般而言，流体的湍动能越大，流速越高，说明气体对该流动区域的卷吸、冲击射流、扰流等作用的能力越强，对边界层的破坏力越大，换热能越强。

图9是当气体入射流速依次为8.0、9.5、11.0、12.5、14.0 m/s时对应的低速流动区域的面积依次为0.004 347、0.003 234、0.002 438、0.001 809、0.001427 m2。这说明低速流动区域的面积逐渐减小，气体在流动区域内的流速明显提高，有助于提升换热效率。

图9 冲击射流流速对低速流动区域面积的影响

3 结论

利用计算流体动力学方法，建立竖直圆管内冲击射流过程中气体流动的数学模型，对气体的流动现象进行深入研究，得到如下结论。

(1)冲击射流过程中，气体的压力损失与气体的入射流速关系密切，当气体的入射流速由8.0 m/s增加至14.0 m/s时，压力损失由93 Pa增加至287 Pa，且这与理论公式计算的趋势一致，计算结果也在偏差允许之内，验证了数学模型的准确性。

(2)气体的入射流速自8.0 m/s增加至14.0 m/s时，气体沿内管内部中心轴线方向和沿喷嘴附近轴线方向运动，流速均呈现“阶梯式”下降，沿喷嘴附近轴线方向运动的气体在临近喷嘴位置时，形成上峰值、“断崖式”下降率和下峰值变化曲线，且气体入射流速越大，曲线变化越显著，此时的低速流动区域面积也由0.004 347 m2减少至0.001 427 m2。

(3)入射气体依次经过各个狭缝喷嘴时，气体脱离喷嘴时的流速明显增加，在外管内冲击射流过程中，气体射流的流速呈非线性衰减现象，衰减速率的“临界点”位于狭缝喷嘴与外管间距的1/2~5/6处，湍动能的峰值则出现在1/4~1/3处。

(4)冲击射流过程中，随着入射气体依次经过各个狭缝喷嘴后，气体在喷嘴中心平面径向上的流速分布由“中心峰值”逐渐转变为“壁面峰值”，且随着气体入射流速的增加，“中心峰值”和“壁面峰值”越发显著。

[1] 杨世铭, 陶文铨. 传热学[M]. 北京: 高等教育出版社, 2006.

[2] Cirillo F, Isopi G M. Glass Tempering Heat Transfer Coefficient Evaluation and Air Jets Parameter Optimization[J]. Applied Thermal Engineering, 2009, 29(5): 1173-1179.

[3] 付天亮, 韩钧, 邓想涛, 等. 特厚钢板射流淬火过程厚向冷速实验研究[J]. 东北大学学报: 自然科学版, 2017, 38(11): 1548-1553.

[4] 刘华坪, 张东飞, 陈焕龙. 端壁射流对高速扩压叶栅性能的影响[J]. 工程热物理学报, 2017, 38(12): 2569-2575.

[5] 桂进乐. 基于微小通道与冲击射流的电子器件冷却机理研究[D]. 武汉: 华中科技大学, 2015.

[6] Baydar E, Ozmen Y. An Experimental and Numerical Investigation on A Confined Impinging Air Jet at High Reynolds Numbers[J]. Applied Thermal Engineering, 2005, 25(2): 409-421.

[7] Jambunathan K, Lai E, Moss M A, et al. A Review of Heat Transfer Data for Single Circular Jet Impingement[J]. International Journal of Heat and Fluid Flow, 1992, 13(2): 106-115.

[8] 陈庆光, 王涛, 吴玉林, 等. 三维湍流冲击射流流动与传热特性的数值研究[J]. 空气动力学学报, 2006, 24(2): 227-232.

[9] 陈翼, 张林进, 叶旭初. 射流混合器内气体湍流扩散过程的CFD数值模拟与实验研究[J]. 过程工程学报, 2007, 7(5): 865-870.

[10] 徐亮, 任德祖, 马永浩, 等. 不同形状喷嘴的旋流冲击射流压力损失和传热特性实验[J]. 航空动力学报, 2018, 33(11): 2678-2686.

[11] 丁祖荣. 流体力学[M]. 北京: 高等教育出版社, 2006.

[12] Ashforth F S, Jambunathan K. Numerical Prediction of Semi-confined Jet Impingement and Comparison with Experimental data[J]. International Journal for Numerical Methods, 1996, 23(3): 295-306.

[13] 杨柳. 真空循环精炼装置内气液两相流动现象的研究[D]. 沈阳: 东北大学, 2012.

[14] Qi F S, Yang L, Liu H J, et al. Flow Structure in RH Vacuum Degasser Using Rotating Electromagnetic Field[J]. Journal of Iron and Steel Research (International), 2012, 19(S2): 888-891.

Numerical Analysis of Turbulent Fluid in Impinging Jet Process in Vertical Circular Tube

YANG Liu1, ZHANG Shuang2, WANG Qian3

（1.Jinzhou Tianyu Electric Furnace CO., LTD，Jinzhou 121000，China; 2.MCC Jingcheng Engineering Technology CO., Ltd, Beijing 100176, China;3.Jinzhou Qiqiqi Microelectronics CO., LTD, Jinzhou 121000, China）

The method of computational fluid dynamics is used to predict fluid flow in impinging jet process. The turbulent model is provided in this paper. The present computational results show good agreement with the theoretical data of pressure loss. When the velocity of the jet gas increases, gas velocity inside the tube decays in a “stepped” shape and gas velocity in the direction of the impinging jet is nonlinearly attenuated. The attenuation mutation is found in the direction of the distance between the slit nozzle and the wall of circle tube. The peak position of turbulent kinetic energy is concentrated in the direction of the distance. When the jet gas is flowing slit nozzles in turn, the circular velocity distribution of horizontal plate in different slit nozzles is determined by the “central peak”, which is gradually replaced by “wall peak”.

impinging jet process; SST turbulent model; turbulence; boundary layer

TK121

A

1674-3261(2021)02-0135-06

10.15916/j.issn1674-3261.2021.02.014

2020-07-26

杨柳(1985-)，男，辽宁锦州人，工程师，硕士。

责任编校：孙 林