海上风电场微观选址工程优化方法与软件开发

白光谱，潘天国，秦琼，王凯，许昌

(1.深圳中广核工程设计有限公司，广东 深圳 518031；2.中国广核新能源华南分公司，广东 深圳 518000；3.河海大学能源与电气学院，南京 211100；4.南京河大风电科技有限公司，南京 211300)

随着能源需求增长与化石燃料资源日趋枯竭的矛盾日益突出，可再生能源越来越受到人们的欢迎和重视，而风力发电是新能源中最具有经济发展前景的发电形式之一[1-2]。近年来，我国风力发电场的开发与建设处于高速发展的阶段，海上风电成为产业发展的趋势。海上风电场由于用海面积有限，同时由于湍流强度低，风电机组的尾流损失比陆上风电场大，使得其排布优化的研究越来越受到人们的关注。目前风电场微观选址一般采用人工经验[3]，将风电机组安装在风资源相对丰富的机位点，沿着盛行风向和垂直盛行风向保留一定间距以避免尾流损失过大。而在海上风电场，风资源状况分布相对均匀，一般成行成列规则布置，且由于海上湍流强度低，尾流恢复慢，风电机组之间的距离需要设计得相对更大，不同的微观选址方案，其风电场的效率和经济性有较大的差别。

已经有一些学者对海上风电场微观选址做了相关研究。Christopher NE4]等人首次对海上风电场优化进行了探讨，选择用贪婪启发式算法和遗传算法的组合来优化计算，在较小的搜索区域中有很大的可能性找到优化的解。RajaiAghabi Rivas[5]等人用模拟退火算法对Horns Rev海上风电场进行了优化，模拟优化结果表明对风况的变化几乎没有敏感性，证明了该方法具有较强的鲁棒性和可行性。Szafron C[6]利用Matlab中的遗传算法工具箱，对海上风电场风机优化排布进行了尝试。Beatriz Pérez[7]等人首先用启发式算法随机设置初始布置，然后用于非线性数学编程技术中，用于局部优化。Hou Peng[8]等人使用了带有多重自适应法的粒子群算法PSO-MAM，对在限定区域优化海上风电场的排布进行了研究，模拟结果表示可以使发电量增长3.84%。但是，现有的优化方法大部分是在理论上进行优化，往往不具有工程实用性；工程中大部分是采用人工经验附加方案比选的传统排布方法，由于受主观因素影响以及比选方案数量有限的原因，往往难以得到令人满意而工程实用的优化解。

在实际工程应用中，广东电力勘测设计研究院和河海大学提出了海上风电场的风电机组排布平行四边形推进方法[9]，理论上可以通过枚举所有平行四边形的排布方案，得到全场发电量最大的工程优化方案。但是，以平行四边形为基本单元的排布有很多个，即便使用高性能的计算机，也需要较长时间才能遍历所有排布方案，往往难以应用。因此，本文提出海上风电场微观选址的优化方法，排布方案通过遗传算法对平行四边形四个网格参数进行优化，在可接受的时间内可以快速得到全场发电量最大的优化排布方案，同时开发工程应用软件，仿真和应用结果表明，提出算法具有提高算法优化效率和海上风电场效率的优点。

1 计算模型

1.1 风频统计模型

有多种估计风速两参数威布尔分布的方法，包括最小二乘法、平均风速和标准差估计法、平均风速和最大风速估计法、矩量法、极大似然法以及能量格局因子法等。本文采用极大似然法，其基本思想是根据子样本观察值出现概率最大的原则，求解母体中未知参数的估计值，由于其具有渐近无偏性、一致性、最近有序性，从而具有计算精度高的优点[10]。在其优化过程中，选取合适的初始值，经过反复迭代，一般可以得到满足收敛条件，得到k和c值。

(1)

(2)

1.2 尾流及其叠加模型

Jensen 尾流模型是海上风电场风能计算中应用最广泛的一种尾流模型[11]，模型如下：

(3)

式(3)中，υ0为自然风速；CT为推力系数；R为风轮半径；k为耗散系数，海上一般取为0.04～0.05；X为两台风电机组之间的距离。

根据某处风电机组与上游风电机组尾流区在风速方向上的投影面重叠程度的不一致，将风电机组之间的尾流相互影响分为完全遮挡、部分遮挡和无遮挡三类。如图1所示，风电机组4与其上游风电机组2属于无遮挡，风电机组5与其上游风电机组1属于完全遮挡，风电机组3与其上游风电机组1属于部分遮挡。当风电机组处于多台风电机组的尾流区时，尾流交汇区风电机组的风速采用平方和模型：

(4)

式(4)中，υj0为不考虑尾流效应时风电机组j的风速；υkj为考虑尾流效应时，在风电机组k的尾流影响下风电机组j的风速；βk为在风电机组j处，风电机组k尾流区投影面积与风电机组j投影面积之比；n为风电场的风电机组数。

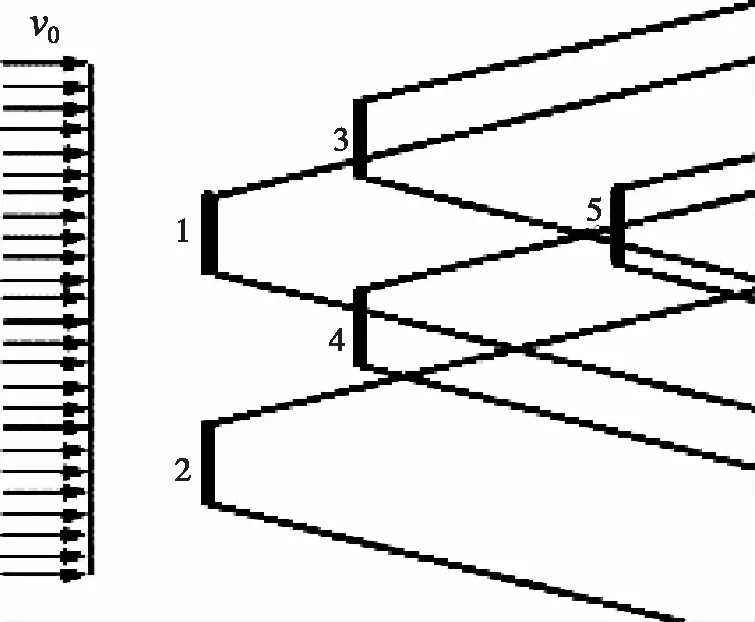
图1 尾流交汇区示意图

根据风机厂家给出的风机功率特性曲线，一般将功率模型近似为一个分段函数，风机发电量计算如下：

(5)

式(5)中，λ和η为功率系数；υcut_in、υcut_out和υrated分别表示切入风速、切出风速和额定风速；Prated表示额定功率。

风电场的发电功率通过概率密度离散法计算。风速呈威布尔分布，在某一风向扇区θ内，风速υ的概率密度为：

(6)

式(6)中，k(θ)和c(θ)为风向扇区θ内的威布尔参数。

单台风机的发电功率为：

(7)

式(7)中，ω(θ)为风向频率。

若风电场中有N台风机，则总发电功率为：

(8)

2 海上风电场风电机组工程排布优化方法

蔡彦枫[11]等人认为在规则型风电机组机位排布中，风电机组呈栅格形式布置，布置的最小单元为平行四边形，网格四参数示意图如图2所示。这类布置形式的风电场风电机组排布由以下网格参数定义：长边所在方位角为α、长边到短边夹角为β、长边单元长度为d1、短边单元长度为d2。

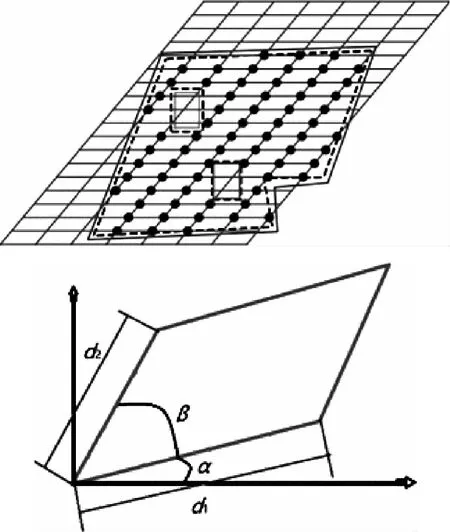
图2 网格四参数示意图

根据风电场边界确定网格区域的范围，在该区域内以平行四边形进行划分，得到若干可选机位点，从而确定一种风电场布局。根据这一原则，对α和β、d1和d2进行遍历取值，以全场发电量最大为优化目标。由于遍历所有平行四边形基本单元得到对应的规则风电场布局会浪费大量时间以及占用大量计算资源，本文针对上述方法进行改进。排布方案采用通过四个网格参数设置实现，并使用遗传算法对网格四参数进行优化，可在更短时间内得到全场发电量最大的风电机组规则排布方案。其中遗传算法[12-13]是模拟达尔文的生物自然选择学说和自然界的生物进化过程的一种自适应全局概率搜索算法，通过选择初始种群进行选择、交叉和变异不断更新产生优质子代，从而得到最优解。该算法具有很强的解决问题的能力和广泛的适应性。其特点在于覆盖面大，利于全局择优，具有很好的收敛性，且计算时间少、鲁棒性高。

海上风电场微观选址优化方法以全场年发电量最大作为优化目标，其优化方法如下：

Step 1：网格四参数设置。

设置平行四边形网格的长边所在方位角为α、长边到短边夹角为β、长边单元长度为d1、短边单元长度为d2的取值范围以及取值数量。α的取值范围为[0，180°]；当β接近 0°或 180°时，风电场内风电机组的排与列布置大致趋近于同一直线，这与实际经验不符，因此β的取值范围为[20°，160°]；d1和d2的取值范围可根据实际海上风电场的行、列间距进行设置，海上风电机组行间距不宜小于3倍风轮直径，列间距不宜小于7倍风轮直径。取值数量为网格四参数在取值范围内的可选值数量，取值数量越大，可遍历的风电机组排布方案越多。

Step 2：遗传算法优化网格四参数。

将网格四参数的取值数量作为优化参数，并运用遗传算法进行优化。先初始化种群，计算个体适应度，从中选取优化的个体遗传到下一代，该种群进行交叉和变异，得到新的种群，重复操作，直到满足终止条件。

Step 3：生成可选机位点集合，从中选取生成规则排布点集合。

Step 4：计算每种排布方案的全场年发电量。

Step 5：判断是否达到迭代次数，若是，则输出全场发电量最大的风电机组排布方案；反之，则跳到Step 2，继续新一次迭代计算。

海上风电场微观选址优化算法流程如图3所示。

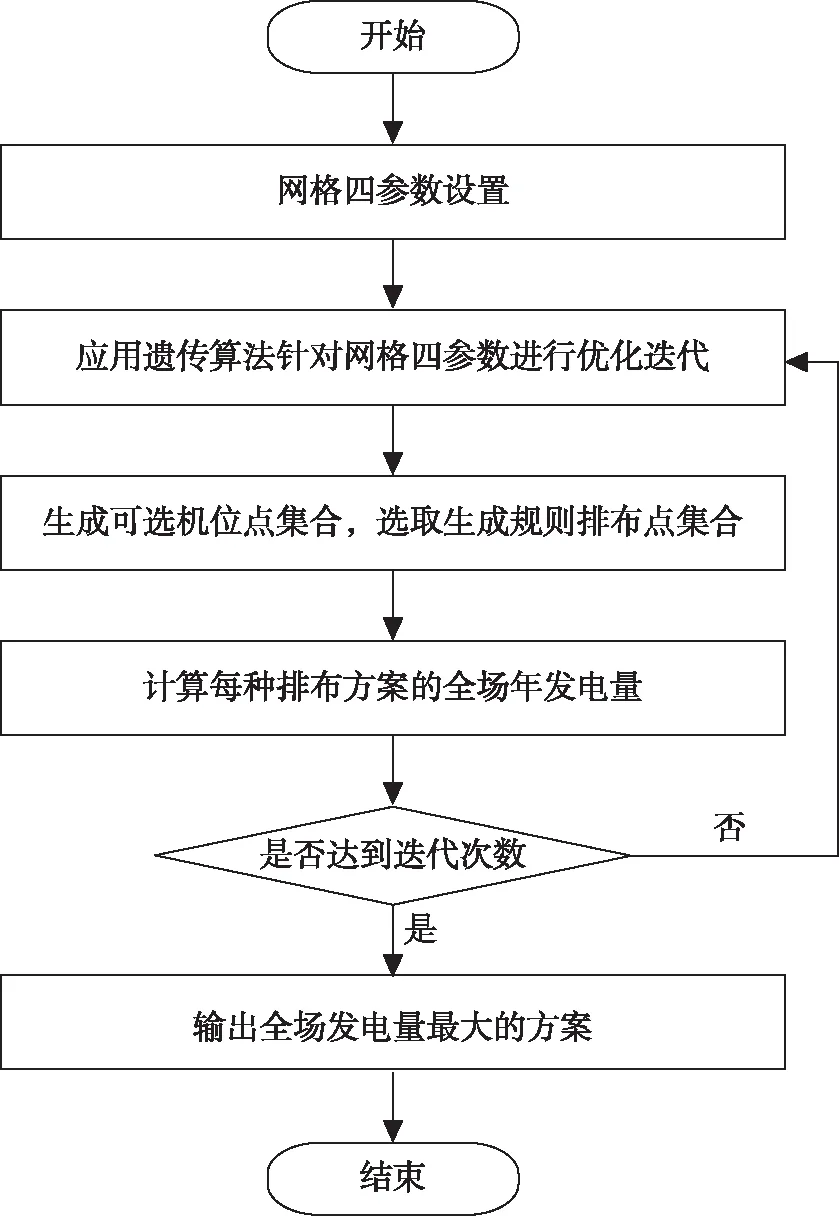
图3 海上风电场微观选址优化算法流程图

3 软件开发与算例应用

本文选取人工经验附加方案比选方法和平行四边形网格枚举方法与工程排布优化方法进行比较。人工经验附加方案比选方法是根据经验得到，受主观因素影响，结果具有局限性。而平行四边形网格枚举即遍历以平行四边形为基本单元的排布方案，对比与本文提出的工程排布优化方法的计算效率有很大差距。针对工程排布优化方法的验证，本文借助Python语言实现了该工程排布优化方法的软件开发，并设计了一种仿真算例和一种工程算例。

3.1 软件开发

本文借助Python语言实现了该工程优化方法的软件开发，风频分布统计模型选用极大似然法，尾流模型选取Jensen模型。软件框架与风电机组优化布局如图4所示。该软件通过设定风电场的边界限定区域、输入风电场的风资源文件和风机参数，并考虑风电场边界等约束条件，以风电场全场年发电量最大为优化目标，得到最优的风电场风电机组排布方案。

3.2 仿真算例

计算模型的风电场为5 km×5 km的矩形区域，空气密度为1.225 kg/m3。风电机组风轮直径为84 m，轮毂高度为70 m，推力系数为0.895。输入某风场实测数据，风电场风电机组数为 60 台，单机容量为2 MW。风电场范围如图5(a)所示，图中粗黑色实线围成的区域为风电场外边界，细黑色实线围成的区域为风电场内边界，五边形为测风塔位置。该风电场的风能玫瑰图如图5(b)所示。

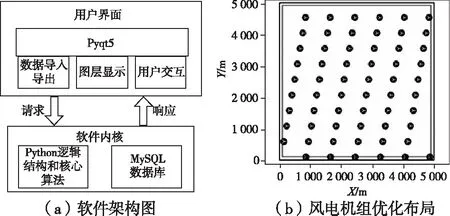
图4 软件框架与风电机组优化布局

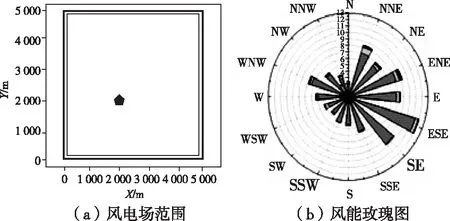
图5 风电场参数

图6为不同方法的优化布局图，表1为不同方法得到的优化布局参数及发电量数据，图7为平行四边形网格枚举法与工程排布优化方法的对比图，横坐标为取值数量，纵坐标分别为全场年发电量以及log(优化时间)。

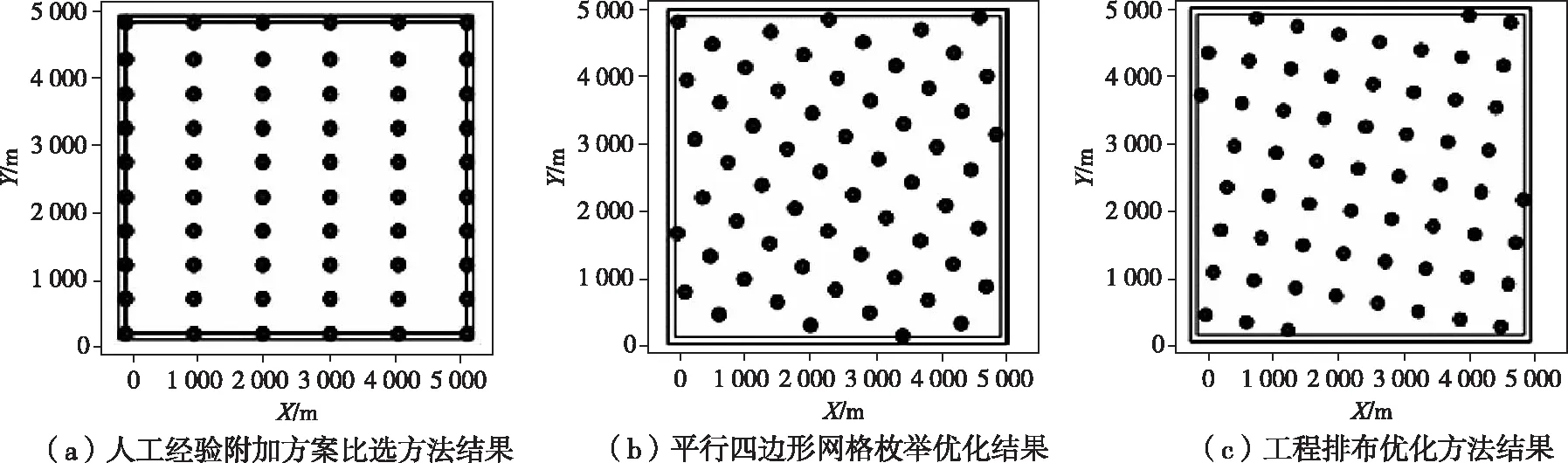
图6 不同方法的优化布局图

表1 不同方法得到的优化布局参数及发电量数据

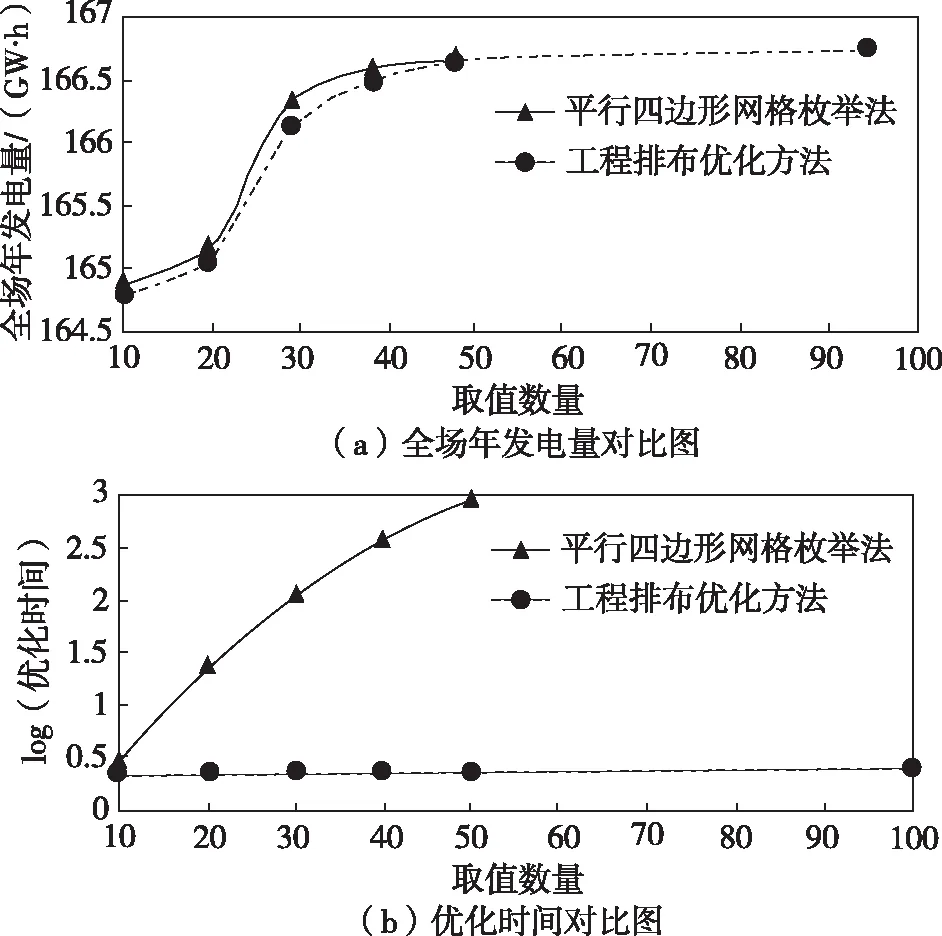
图7 平行四边形网格枚举法与工程排布优化的对比图

结合图6和表1可以看出，人工经验附加方案比选方法虽然排布规则，但是全场年发电量远小于工程排布优化方法。平行四边形网格枚举方法最终得到的全场年发电量也小于工程排布优化方法，而且效率很低，并且会浪费大量计算资源。从图7可以看出，当取值数量相同时，平行四边形网格枚举法的全场年发电量略高于工程排布优化方法，但优化时间远高于工程排布优化方法。随着取值数量的增加，两种方法的全场年发电量都会增大，但增大到一定程度发电量就无明显变化。两种方法的优化时间也随取值数量的增加而增大，平行四边形网格枚举法的优化时间呈指数增长，而工程排布优化方法的优化时间呈线性增长。

3.3 工程算例

以江苏某海上风电场为例，在该风电场范围内布置 37 台 3 MW 的风电机组。风电场范围如图8(a)所示，图中外框粗实线围成的区域为风电场外边界，内框细实线围成的区域为风电场内边界，五边形为测风塔位置。该风电场位于江苏沿海，风电场大小为 6 km×3.5 km。该风电场的风能玫瑰图如图 8(b)所示。风电机组的轮毂高度为 90 m，叶轮直径为 110 m，推力系数为 0.8。风电机组的切入风速为3 m/s，切出风速为 25 m/s，额定风速为 12 m/s。

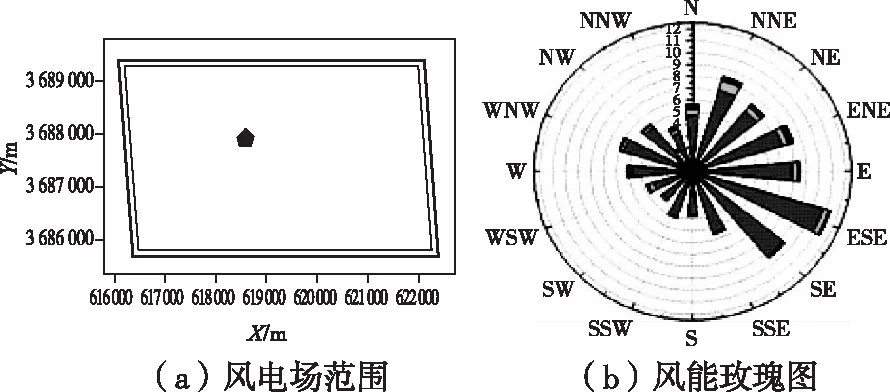
图8 风电场参数

图9为不同方法的优化布局图，其中人工经验附加方案比选方法结果借鉴了该海上风电项目的可行性研究报告排布方案进行机位布置，更具对比性。表2为不同方法得到的优化布局参数及发电量数据。图10为平行四边形网格枚举法与工程排布优化方法的对比图，横坐标为取值数量，纵坐标分别为全场年发电量以及log(优化时间)。

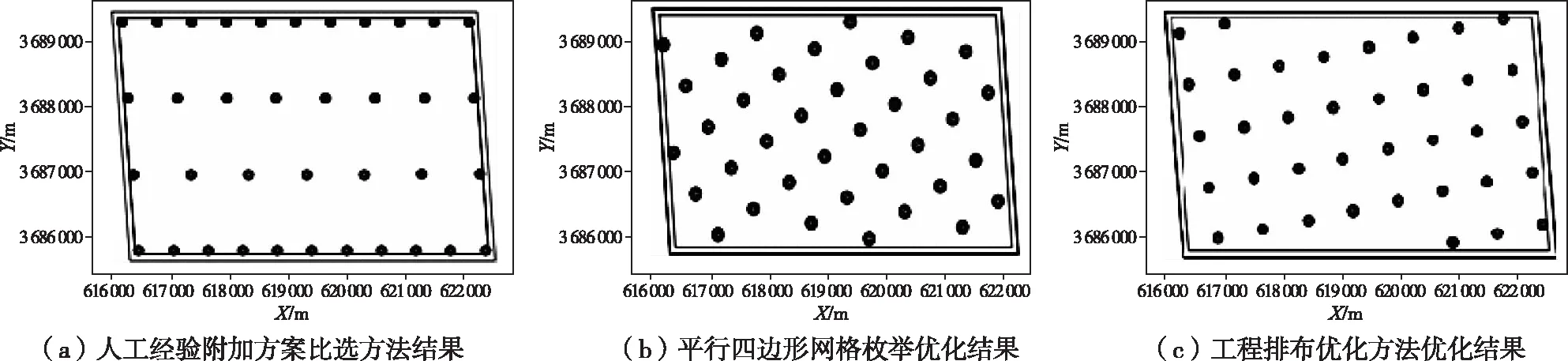
图9 不同方法的优化布局图

表2 不同方法得到的优化布局参数及发电量数据

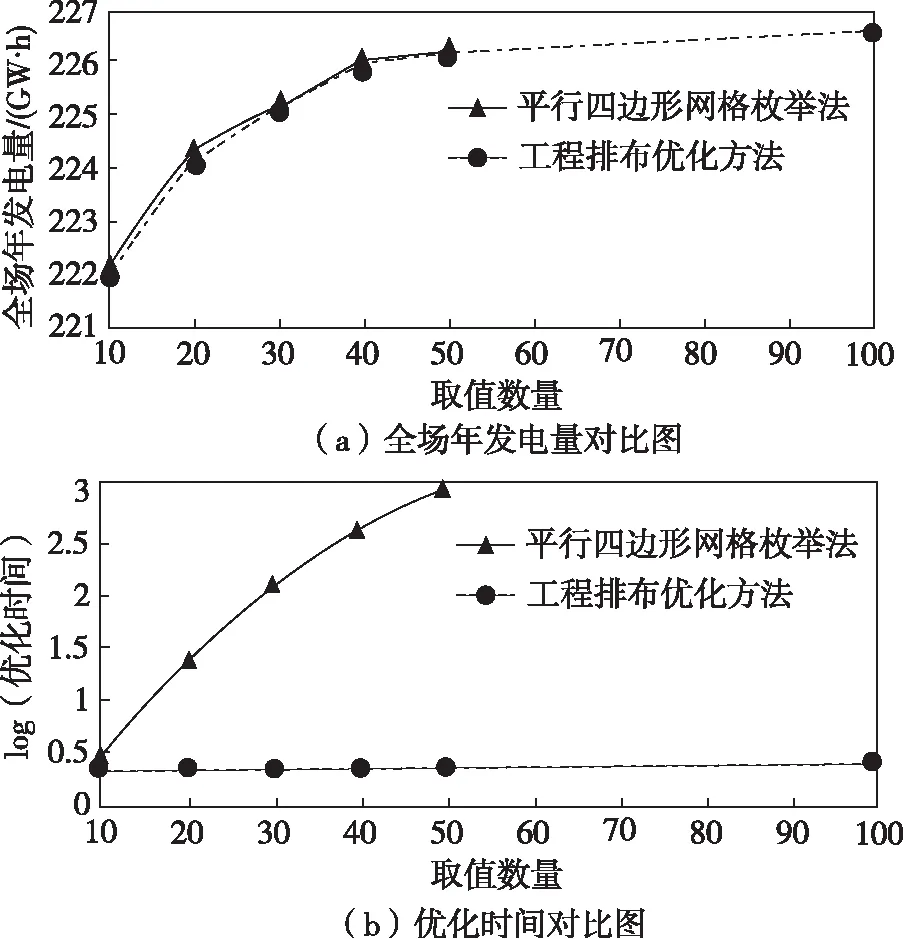
图10 平行四边形网格枚举法与工程排布优化方法的对比

结合图9和表2可以看出，人工经验附加方案比选方法的优化布局中，虽然是规则排布，但难以充分利用风电场范围内的风资源，故全场净发电量远低于工程排布优化方法。平行四边形网格枚举的优化布局中，最终得到的全场年发电量略小于工程排布优化方法，计算效率很低，并且会浪费大量计算资源。而在本文提出的工程排布优化方法的优化布局中，风电机组排布规则均匀，充分利用了风电场区域，而且能快速得到最优的风电机组布局，不但优化效率高，而且可以节省大量计算资源。从图10可以看出，当取值数量相同时，平行四边形网格枚举法的全场年发电量略高于工程排布优化方法，但优化时间远高于工程排布优化方法，可见前者优化效率低。两种方法的全场年发电量随取值数量的增加而增大，但增大到一定程度发电量就无明显变化。两种方法的优化时间也随取值数量的增加而增大，其中平行四边形网格枚举法的优化时间呈指数增长，而工程排布优化方法优化时间呈线性增长。

4 结语

海上风电场风电机组工程排布优化方法研究具有实际应用价值，该方法采用四个网格参数设置实现排布方案，并使用遗传算法对网格四参数进行优化，优化效率高，节省大量计算资源，可以得到符合工程要求的风电机组规则排布方案。在海上风电场风电机组排布优化过程中，本文使用工程排布优化方法求解。通过对仿真算例和工程算例的应用分析，并对比人工经验附加方案比选方法以及平行四边形网格枚举方法，工程排布优化方法得到的风电机组排布均匀，风电场区域分布均匀合理，排布方案发电量高，具有优化精度高、速度快的优点，该方法的优化结果与工程经验相符，可以为实际工程应用提供参考。