汲水斗对水面飞行器水动力性能的影响

王晓强，来曙光，肖志坚

1 海军装备部驻武汉地区第二军事代表室，湖北 武汉 430064

2 中国舰船研究设计中心，湖北 武汉 430064

3 中国特种飞行器研究所，湖北 荆门 448035

4 高速水动力航空科技重点实验室，湖北 荆门 448035

0 引 言

相比传统消防手段，大型水面飞行器参与森林灭火具有多种优势，例如机动性强、速度快、载水量大等[1]。目前，国内外学者经过多年的研究和实践，已完成水面飞行器投汲水灭火系统的系列发展，并在实际应用中取得了显著成效。在水面飞行器汲水装置方面，目前国内外已公开的相关研究和文献极少，主要集中在水面飞行器整体的气−水动力性能方面。1959 年，Mottard[2]研究了水上飞机起飞过程中波浪对阻力的影响。2012 年，王永亮等[3]根据炸弹的连续计算投放点（CCRP）原理，获得了投水算法的数学模型，最后结合自由紊动射流原理，提出了一种大型灭火飞机的投水算法。2015 年，黄淼等[4-5]对水陆两栖飞机模型波浪试验技术、飞机在波浪上的运动响应以及船体水动力矩特性进行了深入研究。2019 年，段旭鹏等[6]基于CFD 方法研究了水上飞机泊水时的空气和水动力性能。

由于缺乏相关的研究，根据水面飞行器汲水斗的设计需要，本文拟开展如下研究：通过开展静水拖曳试验，研究汲水斗放下时不同汲水量下飞行器的阻力和姿态随速度的变化规律；通过数值仿真分析，研究汲水斗的汲水效率、汲水载荷和附加俯仰力矩随速度的变化规律，以及无、收起和放下汲水斗3 种条件下水面飞行器的阻力、升沉和纵倾等水动力特性的变化规律。

1 几何模型与方法

1.1 几何模型

以某水面飞行器无动力模型为试验和仿真对象，开展静水拖曳试验（EFD）和仿真计算（CFD）。试验和数值计算的工况如表1 所示。首先，开展汲水斗放下时3 种排水量（0.79Δa，0.85Δa和Δa）的水面飞行器静水拖曳试验；随后，开展排水量为Δa时水面飞行器在无、收起和放下汲水斗条件下水动力性能的仿真计算。试验模型和仿真对象如图1 所示，无汲水斗、汲水斗收起和放下这3 种工况下的几何示意图如图2 所示。

表1 试验和数值计算的工况Table 1 Conditions of experiment and numerical simulation

图1 模型的几何特征Fig. 1 Features of the studied model

图2 3 种工况下汲水斗状态几何示意图Fig. 2 Features of bailer under three conditions

1.2 网格划分

本文采用切割体网格生成高质量的壁面网格，通过体积控制的方法对复杂曲面或者流动分离严重的区域进行加密处理，例如自由液面、机身断阶吃水区域、各操纵面等。采用重叠网格解决飞机运动问题，同时，对重叠区域内的近壁面进行加密处理以精确捕捉近壁面流动。为保证空气动力和水动力性能计算结果的准确性，分别考虑操纵面和船身边界层的设置：各操纵面表面平均壁面y+值为1，边界层层数15 层；机身表面平均壁面y+值为5，边界层层数8 层。模型表面网格如图3 所示。

图3 模型网格分布Fig. 3 Mesh distributions of the model

网格计算域为：−1.0L≤x≤4.5L，−1.5L≤y≤1.5L，−1.0L≤z≤1.0L，其中x，y，z分别为计算域长度、宽度、高度方向的坐标值，L为水面飞行器的总长。由于模型几何对称，可采用一半模型进行仿真模拟，因此对称面采用对称面边界条件，上游入口采用速度入口，下游出口采用压力出口，上边界、侧边和下边界采用速度入口边界条件；在模型表面定义无滑移的壁面边界条件。计算域的边界条件设置如图4 所示。

图4 计算域边界条件Fig. 4 The applied boundary conditions

采用RANS 方法求解，湍流模型采用SSTk-ω湍流模型[7]。采用二阶迎风有限体积法（FVM）对控制方程进行离散化。对流项采用二阶迎风格式离散，扩散项采用二阶格式离散。自由液面捕捉采用两相流体体积（VOF）技术。

2 拖曳试验

2.1 试验设计

真实的水面飞行器在汲水后会将汲取的水储存在飞机特定的水箱中，而此次试验中流经汲水斗的水通过汲水系统的管路从飞行器侧面排出，根据需要，在拖车启动之前，需将特定质量的水提前注入模型水箱。

试验在拖车的前伸装置上进行，如图5 所示。图5 所示模型的螺旋桨固定，不影响仿真与试验结果分析对比。前伸装置试验装置主要包括拖车、前伸装置、运动装置和限位装置。其中，前伸装置与拖车固结，用于将试验模型的位置前伸至拖车前部；运动装置是保证飞机自由度的安装装置，包括小滑车、升沉杆和重心连接杆，小滑车能在前伸装置上沿航向在一定范围内前、后移动，保证模型能沿航向自由平移，升沉杆穿过小滑车与重心连接杆上端固结，试验时升沉杆随模型垂向平移，以保证模型能自由升沉运动，重心连接杆下端在重心位置与模型铰接，以保证模型能自由俯仰运动；限位装置主要是对模型的偏航运动进行限制，避免模型试验时出现偏航运动致使模型与池壁发生碰撞而发生危险，限位功能通过导航杆实现。

图5 试验装置示意图Fig. 5 Experimental layout

2.2 试验数据

图6～图8 所示为工况1～3 的阻力和姿态试验结果。由图可知，随着速度V的增大，各工况的无量纲总阻力系数（Ft/Δ）和无量纲升沉系数（Heave/L）增大，纵倾角减小；汲水量增大，其无量纲总阻力系数、纵倾角、无量纲升沉系数也增大。本文中升沉以上升为正，纵倾以艉倾为正。

图6 无量纲总阻力系数试验结果Fig. 6 Experimental dimensionless total drag coefficient

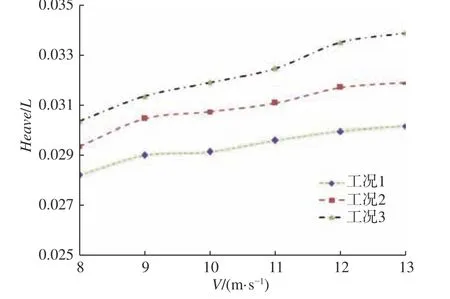
图7 无量纲升沉系数试验结果Fig. 7 Experimental dimensionless heave coefficient

图8 纵倾角试验结果Fig. 8 Experimental trim angle

3 数值方法模拟

3.1 数值方法验证

以工况3 和工况6 为例，通过对比汲水斗放下时水面飞行器模型的试验和仿真计算结果，开展数值计算方法的验证。几何模型及网格划分如第2 节所述。

如图9 和图10 所示，试验中，不同速度下无量纲总阻力系数、无量纲升沉系数和纵倾角的趋势与数值计算结果吻合较好，验证了本文所采用计算方法的合理性和准确性。从图9 中可看出，计算得到的水阻力均小于试验值，这可能是因为相比物理试验，数值计算中并没有考虑池壁效应的影响，同时，软件自身的自由液面捕捉模型无法完全模拟高速滑行时模型的喷溅阻力的原因。

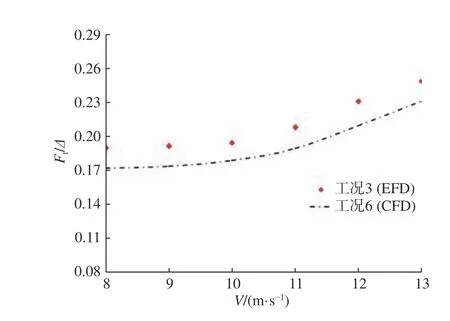
图9 无量纲总阻力系数的试验和仿真计算结果对比Fig. 9 Comparison of experimental and computed dimensionless total drag coefficient

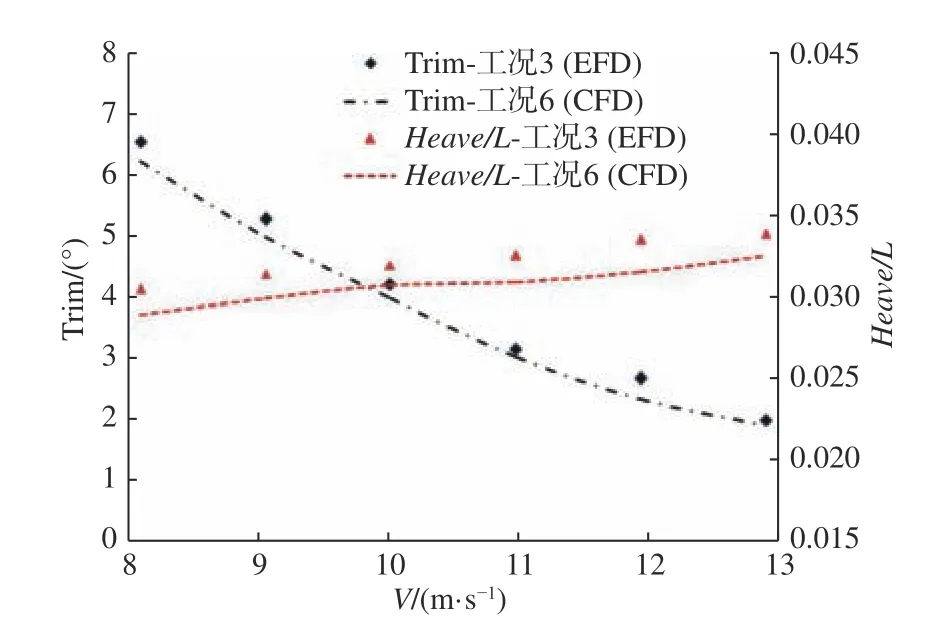
图10 姿态的试验和仿真计算结果对比Fig. 10 Comparison of experimental and computed attitudes

3.2 汲水斗的汲水效率和汲水载荷

由于需要在规定的时间内完成指定的汲水量，因此本文通过计算汲水斗的流量来分析汲水斗的汲水效率随速度的变化规律。由图11 可知，汲水斗的流量Q（单位：kg/s）是随速度V（单位：m/s）的增大而增大的，且两者呈非线性关系，因此采用二次多项式函数进行拟合，得到

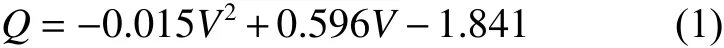
通过对比流量的计算值和拟合值，可以发现采用二次函数能很好地拟合汲水斗流量与速度之间的关系。不同速度下汲水斗入口的体积分数分布如图12 所示。汲水斗浸水面积是随着速度变化的，因此，汲水斗的汲水效率并不与速度成正比关系。

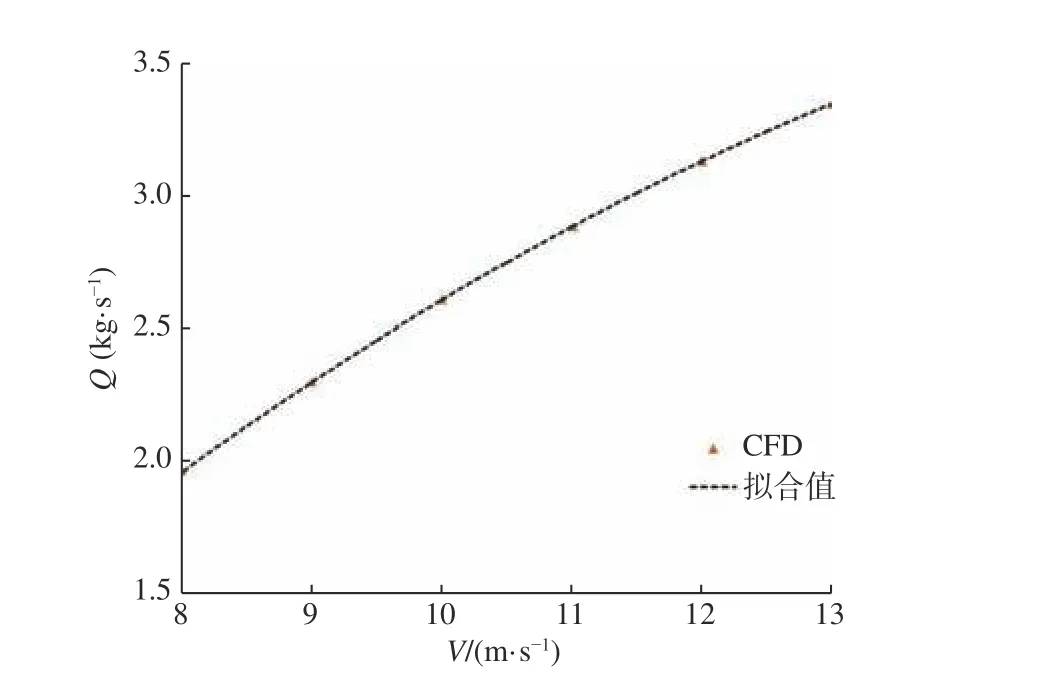
图11 流量的计算值和拟合值对比Fig. 11 Comparison of computed mass flow and fitting value

图12 汲水斗入口处的体积分数分布，8 m/s（a）和13 m/s（b）Fig. 12 Volume fraction of water at speed of 8 m/s (a) and 13 m/s (b)

在汲水过程中，在满足汲水效率的同时，也需要关注汲水斗上的受载和产生的附加俯仰力矩，以免造成结构损坏和飞行器失控。以V=13 m/s为例，由图13 可知，汲水斗放下时，汲水斗内部的压力分布整体明显大于汲水斗外部，汲水斗的受载可以分解为水平的阻力（Fx）和竖直向下（Fz）的拉力。图14 表明，汲水斗收起时，升阻力系数均在0.002 以内，汲水斗的受力几乎可忽略；而汲水斗放下时，阻力系数从0.02 增大至0.051，升力系数从0.018 增大到0.044，汲水斗受力明显增大，且随着速度的增大，Fx和Fz均呈非线性增长。图15表明，汲水斗收起时，汲水斗产生的附加俯仰力矩系数在0.20 以内，几乎可以忽略；而汲水斗放下时，汲水斗对机身产生的附加俯仰力矩系数随着速度的增大，从1.59 增加至3.97，呈非线性增长。因此，在设计汲水斗时需要重点考虑汲水斗放下时汲水斗受力及产生的附加俯仰力矩。

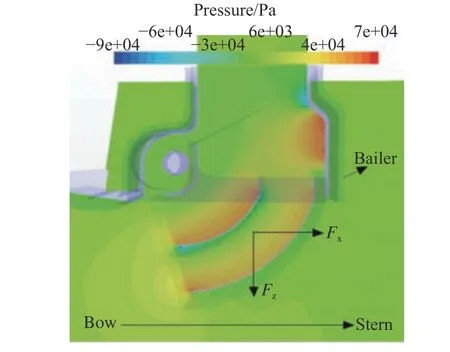
图13 V=13 m/s 时汲水斗内、外部压力分布Fig. 13 Pressure distribution of bailer at the speed of V=13 m/s

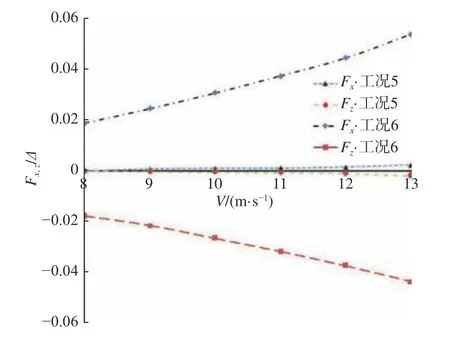
图14 无量纲力系数计算值Fig. 14 Computed dimensionless force coefficients

图15 无量纲力矩系数计算值Fig. 15 Computed dimensionless moment coefficients

3.3 汲水斗对飞机总阻力的影响

图16 所示为计算得到的3 种状态下无量纲总阻力系数随速度的变化曲线。由图16 可以看出，无汲水斗和汲水斗收起这2 种情况下的总阻力较为接近，且随着速度的增大均表现出先减小后增大的趋势，变化幅度较小。相比之下，汲水斗放下时总阻力明显增大，且随速度近似呈二次曲线增长。图17 所示为相对于无汲水斗情况，汲水斗收起和放下时引起的阻力增长率随速度的变化情况。随着速度的增大，同无汲水斗情况相比，汲水斗收起时的阻力增量较小，从2.6%增大到了6.0%，而汲水斗放下时的阻力增加较为明显，是随速度的增大而增大，从47.2% 增大到了95.7%。因此相对于无汲水斗情况，汲水斗收起时，对总阻力影响很小，而汲水斗放下时阻力急剧增加，且增幅随速度的增大而增大。

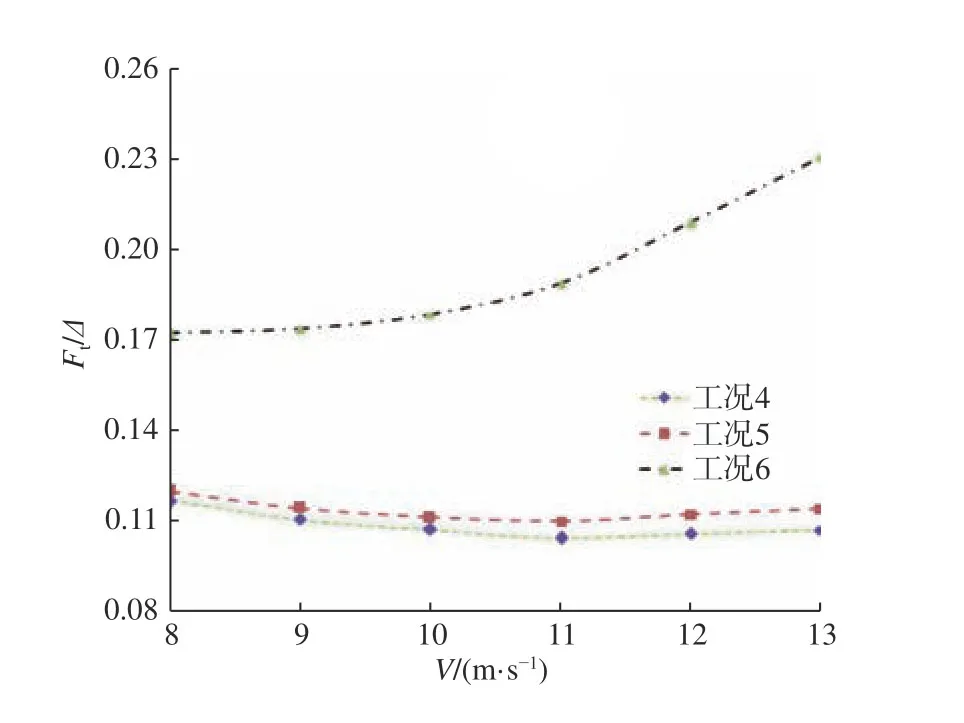
图16 无量纲总阻力系数随速度的变化规律Fig. 16 Variation of dimensionless total drag coefficient with respect to speed

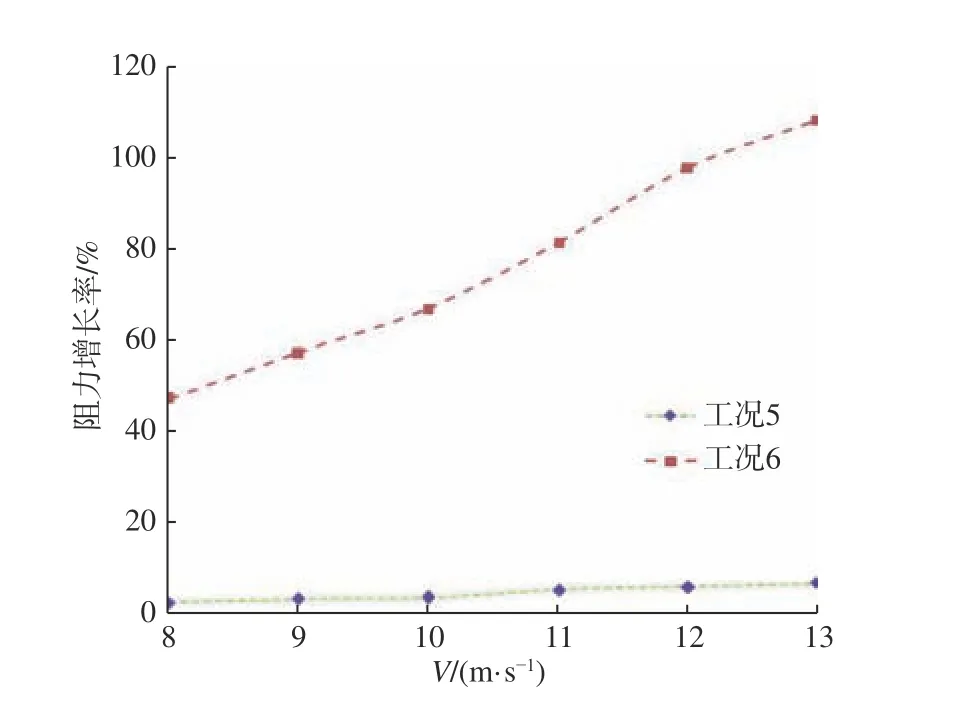
图17 无量纲总阻力系数随速度的变化规律Fig. 17 Variation of dimensionless total drag coefficient with respect to speed

3.4 汲水斗对滑行稳定性的影响

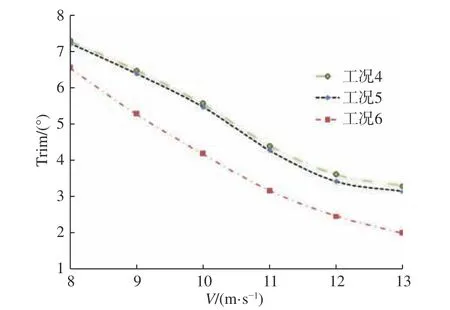
图18 各工况纵倾角随速度的变化规律Fig. 18 Variation of trim angle with respect to speed under different conditions

图18 为3 种情况下机身纵倾角随速度的变化曲线。由图18 可以看出，随着速度的增大，在3 种情况下机身的纵倾角均随速度的增大而减小，相比无汲水斗情况，汲水斗收起时的机身纵倾角与其相差很小，而汲水斗放下时的纵倾角则明显减小。由图15 可知，汲水斗放下时，汲水斗产生了较大的附加俯仰力矩，抑制了机身的尾倾，因此汲水斗放下情况下的纵倾角幅值明显减小；而汲水斗收起时产生的附加俯仰力矩非常小，可见汲水斗收起和无汲水斗时纵倾角幅值相差很小。图19 所示为3 种情况下机身无量纲升沉系数随速度增大的变化曲线。由图19 可知，随着速度的增大，3 种情况下机身的升沉幅值均随速度的增大而减小了；汲水斗收起与无汲水斗时的纵倾角相差很小，而汲水斗放下时的纵倾角明显大于其他2 种情况。虽然由图14 可知，当汲水斗放下时，汲水斗受到向下的拉力，但是通过分析整个汲水系统（汲水斗加管路）的受力情况，整个汲水系统在所计算速度范围内产生了2.3%～5.1%的升力，因此汲水斗放下时机身的上升幅度会大于其他2 种情况；而当汲水斗收起时，水流不经过汲水系统，且汲水斗处于机身断阶之后，垂向上受力极小，因此汲水斗收起时和无汲水斗时的升沉幅值相近。

图19 无因次升沉系数随速度的变化规律Fig. 19 Variation of Heave/L with respect to speed at different conditions

图20、图21 所示分别为速度V=13 m/s 时汲水斗放下情况下自由液面分布的仿真计算结果与试验结果。由图20 所示的仿真计算结果来看，水面飞行器高速滑行时产生的凯尔文角较小，兴波主要集中在后体区域，且可以观察到断阶区域喷溅出的水浪贴近后体表面，具有吸附现象。兴波波幅从飞行器船身断阶处开始增大至尾部开始衰减，水流从汲水系统的出水口喷射而出，随即落入水面。由图21所示的试验结果也可以观察到上述相似现象，从整体来说，试验与仿真得到的自由液面的分布吻合较好。

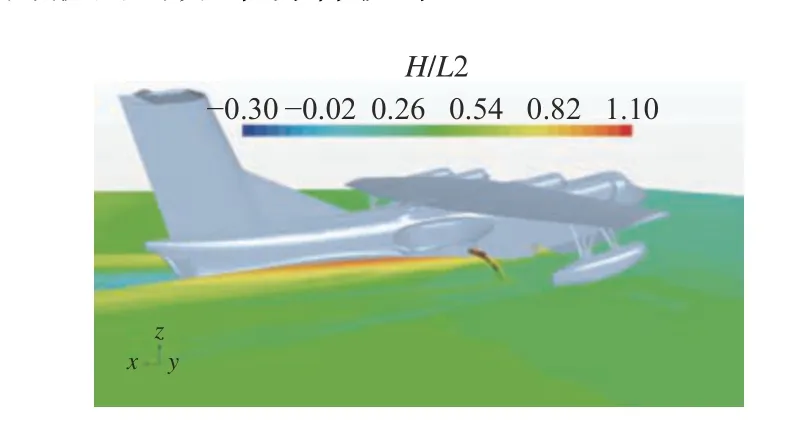
图20 V=13 m/s 时仿真计算得到的自由液面分布Fig. 20 Computed free surface at speed of V=13 m/s

图21 V=13 m/s 时试验得到的自由液面分布Fig. 21 Experimental free surface at speed of V=13 m/s

4 结 论

本文通过开展试验和数值计算，主要得到如下结论：

1) 试验结果表明，随着速度的增大，相同汲水量下的总阻力、升沉幅度均增大，纵倾角减小；汲水量增大时，总阻力、升沉幅度、纵倾角均增大。

2) 汲水斗的流量随速度的增大而增大，且两者呈非线性关系，采用二次函数可以很好地拟合汲水斗流量与速度之间的关系。汲水斗放下时，汲水斗上的阻力系数从0.02 增加到了0.051，升力系数从0.18 增加到了0.44，附加俯仰力矩系数从1.59 增加到了3.97，三者均随着速度的增大而呈非线性增长。汲水斗收起时，其受力和力矩均可忽略。

3) 仿真计算结果表明，汲水斗放下时水面飞行器的总阻力明显增大，且随着速度的增大，相对于无汲水斗情况，总阻力增量从47.2%增大到了95.7%。与此同时，汲水斗放下后，水面飞行器的升沉将增大，纵倾角减小。汲水斗收起时，汲水斗对水面飞行器水动力性能的影响可以忽略。