基于VMD-GRU的电力短期负荷预测方法

黄冬梅，唐 振，胡安铎，孙锦中

（上海电力大学 电子与信息工程学院，上海 200090）

0 引 言

负荷预测是关系到电力系统安全与稳定的重要问题，提高电力负荷预测的精度对电网的可靠性和经济性有重要意义。在电力物联网时代，由于多重复杂因素的影响，电力负荷呈现出较强的非平稳性，电力短期负荷预测面临着更大的挑战[1]。

电力负荷预测方法大体上可以分为两大类。一类为统计学方法，包括趋势外推法、回归分析法等。统计学方法相对简单，但非线性拟合能力有限。另一类为机器学习方法，包括Elman神经网络[2]、人工神经网络[3]等。机器学习方法具有很好的非线性拟合能力，但随着大数据时代的到来，传统的机器学习方法对于数据量较大的预测问题能力有限，深度学习方法逐渐成为研究的焦点，其中的长短期记忆（Long Short-Term Memory, LSTM）网络常被用来进行负荷预测[4-6]。门控循环单元（Gated Recurrent Unit, GRU）对LSTM进行了改进，将其两个门结构合成为一个门，因此训练参数较少，收敛速度更快，同时预测性能良好，在电力负荷预测及其他领域广泛应用[7-11]。但是使用单一的方法进一步提升电力负荷预测的精度受到限制。

为了进一步提高负荷预测的精度，逐步发展出多种组合预测模型。组合预测方法的基本思想是使用多种方法预测，将多种方法的预测结果叠加作为最终的预测结果，或者将负荷序列分解为多个分量，对各分量分别建模预测，将预测结果叠加为最终预测值[12-17]。负荷序列分解的方法有小波变换、经验模态分解（Empirical Mode Decomposition, EMD）等。其中EMD是组合预测模型中常用的序列分解方法，但是EMD存在模态混叠现象，会影响负荷预测的精度。

本文考虑采用变分模态分解（Variational Mode Decomposition, VMD）的负荷序列分解方法，提出一种基于VMD-GRU的短期负荷组合预测模型。该模型采用VMD方法将负荷序列数据进行分解，将其分解为一系列特征互异的模态分量，以降低负荷原始序列的复杂性和非平稳性，分别对每个模态分量建立GRU网络预测模型，最终将预测结果组合重构作为负荷预测值。使用同一负荷数据，采用了LSTM、GRU以及EMD-LSTM、EMD-GRU、VMD-LSTM、VMD-GRU 4种组合方法进行对比实验，说明本文所提的基于VMD-GRU的模型预测效果良好。

1 电力短期负荷预测研究方法

1.1 VMD方法

由分解的条件得到的约束变分问题可以表达为：

式中：uk表示第k个模态函数；ωk表示第k个模态函数的中心频率。

为使问题转换为非约束问题，同时引入拉格朗日乘子λ和二次惩罚项，得到扩展的拉格朗日表达式为：

原来的极小化问题的解可看成是扩展的拉格朗日表达式的鞍点，采用交替方向乘子法求解此鞍点，求得uk及ωk：

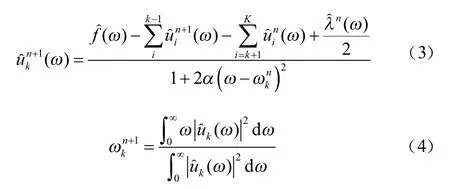
VMD分解得到的模态分量分别表征不同频域的特征分量，VMD可有效分解原始信号中特征互异的分量，同时相比EMD可能以更少的模态分量实现信号的分解。

1.2 GRU原理

GRU网络能够很好地学习时间序列数据内部动态变化规律，GRU结构中保留了LSTM结构中的单元的信息流。图1给出了GRU原理的示意图，其中ht-1为t-1时刻隐藏层输出，xt为t时刻的输入。网络内部设置更新门zt和重置门rt，其中更新门控制遗忘和更新，重置门用于控制当前状态中哪些部分用于计算下一目标状态。

图1 GRU原理

t时刻GRU单元中的更新门z的计算如下：

式中：σ表示sigmoid函数；Wz和Uz表示更新门的权重系数。

重置门r的计算公式可以写为：

式中，Wr和Ur表示重置门的权重系数。

式中：“*”表示Hadamard乘积。

t时刻的输出为：

2 VMD-GRU组合预测模型

2.1 VMD-GRU预测模型框架

图2给出本文所提模型的框架，本文所提出的VMDGRU方法包括分解、分量预测、预测结果重构3个阶段。

图2 VMD-GRU模型框架

（1）采用VMD方法将原始负荷序列分解为多个特征互异的模态分量。相对于原始的负荷数据，各分量的变化趋势及特征更有规律性，有利于提升负荷预测的精度。

（2）对各模态分量进行归一化处理，将每一个模态分量数据分为训练集和测试集，并对每个分量分别建立GRU网络学习其内部动态变化规律，使用Adam算法，根据损失函数对GRU网络进行更新。

（3）将各分量的预测结果分别进行反归一化处理，重构叠加各分量的预测值，可以得到最终的负荷预测结果，并根据实际负荷值对负荷预测结果计算预测性能指标。

2.2 预测评价指标

为评价预测模型的性能，采用平均绝对百分误差（MAPE）和均方根误差（RMSE）作为评价指标，定义如下：

式中：yi为预测值；y'i为实际值；n为样本数量。

3 算例分析

选取某地区2016年1月1日至2016年7月30日整点负荷数据作为训练集数据，共5 112个数据，对7月31日的负荷进行提前24 h预测。本文采用Keras框架建立模型，建立2组对比试验，单一模型LSTM、GRU及加入分解方法的组合模型EMD-LSTM、EMD-GRU、VMD-GRU、VMDLSTM，并对它们的预测效果进行比较。其中，VMD-GRU、LSTM、GRU、VMD-LSTM、EMD-LSTM、EMD-GRU 模型结构参数均采用50-100-1，即采用双隐含层结构，分别取50个和100个神经元，输出层取1个神经元。

3.1 单一模型对比分析

为验证GRU网络的预测性能，选择了将LSTM、GRU进行预测效果对比，预测结果对比如图3所示。由图可知GRU网络的拟合效果明显优于LSTM网络，其中GRU网络预测结果的MAPE和RMSE指标分别为3.422%和54 489.582 kW，相比LSTM网络的预测结果分别降低了24.3%和17.4%。

图3 单一模型预测结果对比

LSTM、GRU网络的损失函数衰减对比如图4所示，可以看出GRU网络相比LSTM网络收敛速度更快。这是由于GRU相对LSTM的训练参数少。因此，对于需要考虑时效性的短期负荷预测，GRU网络比LSTM更加具有优势。

图4 GRU与LSTM网络的收敛速度

虽然从评价指标上看，使用GRU网络的负荷预测优于LSTM网络，但是由于模型单一及原始负荷数据非平稳性的影响，单一模型的预测精度难以持续提升。为了进一步提升预测精度，组合预测模型成为负荷预测领域的重要方案。

3.2 组合预测方法的对比分析

分别采用EMD和VMD对原始负荷数据进行分解，结合LSTM和GRU预测模型，构建了EMD-LSTM、VMDLSTM、EMD-GRU、VMD-GRU 4种组合预测模型。图5给出了4种组合预测模型的预测结果。

图5 各组合模型预测结果对比

由图5与图3的对比可以看出，结合分解方法的组合预测模型相比单一模型拟合效果更好，尤其体现在负荷峰谷处数据上。如图5所示，在组合模型中，VMD-GRU模型在负荷的变化趋势和峰值负荷两个方面都明显优于其他方法。

为了定量评价各组合预测模型，表1给出了各组合模型的预测结果的平均绝对百分误差和均方根误差。从表1中的MAPE和RMSE指标上看，组合预测都明显优于第3.1节所示的单一模型，其原因在于加入分解方法的组合预测模型先分解后预测，可以降低原始负荷数据非平稳性对预测结果的影响，能够更好地学习负荷序列内部变化规律。

表1 各组合模型的预测精度结果

表1所示的4种组合模型可以分为2类：一类是结合EMD分解的预测模型；另一类是结合VMD的预测模型。从表1可以看出，基于VMD分解的模型性能优于基于EMD分解的模型。本文提出的基于VMD-GRU的预测模型在MAPE和RMSE两项指标上，均取得了四个组合预测模型中最好效果，MAPE误差仅有2.081%，相比EMD-GRU模型降低了15.7%，正是因为VMD有效地解决了模态混叠问题，其分解效果更好。VMD和EMD分解结果分别如图6和图7所示，其中图6（a）和7（a）显示的VMD、EMD分解的模态分量，图6（b）和7（b）为信号对应的频谱。

从图7（b）中可以看到IMF2与IMF3两个模态分量存在明显的频谱混叠现象，而图6（b）中VMD分解的各模态函数较好的避免了模态频谱混叠。此外，从图6（a）中模态分量与原始负荷的对比可以看出，模态分量u1与原始负荷信号的变化趋势相似性较大，因此可以作为负荷变化的趋势特性，且高频分量的变化更具规律性，而且幅值较小，对于总体预测精度影响较小。结果表明，VMD对于负荷数据的分解更具有效性。

图6 VMD分解结果

图7 EMD分解结果

为验证本文VMD-GRU组合模型的时效性，表2所列为四种组合预测模型所需的总运行时间。

由表2可以看出，VMD-GRU预测模型运行时间明显低于其他三种组合模型。这是因为VMD方法采用自适应的分解方法，可以解决模态混叠问题，且以更少的模态分量实现序列的分解，有效降低模型的复杂度。另一方面，由于GRU相对LSTM的训练参数少，训练时间短，收敛速度更快，进一步降低了本文组合模型的运行所需时间。

表2 四种组合预测模型总运行时间

4 结 语

本文从数据平滑的角度提出一种基于VMD-GRU的短期负荷预测模型。本文模型利用VMD对电力负荷数据进行更有效地分解，有效地解决了传统分解方法模态混叠的问题，有利于提升负荷预测的精度；对各分量分别采用GRU网络建模预测，利用GRU网络预测性能好且收敛速度快的优势，进一步提升了模型的预测精度。算例结果表明，VMD-GRU模型表现出良好的性能和拟合效果，可以提升电力短期负荷预测效果。